每日学习一个数据结构-AVL树
文章目录
- 概述
- 一、定义与特性
- 二、平衡因子
- 三、基本操作
- 四、旋转操作
- 五、应用场景
- Java代码实现
概述
AVL树是一种自平衡的二叉查找树,由两位俄罗斯数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明。想了解树的相关概念,请点击这里。以下是对AVL树的详细说明:
一、定义与特性
- 定义:AVL树是一种二叉查找树,其中每个节点的左右子树的高度差的绝对值(即平衡因子)不超过1。
- 特性:
- 左右子树都是AVL树。
- 左右子树高度之差(简称平衡因子)的绝对值不超过1(-1、0、1)。
- 任意节点的左右子树的高度差不会超过1,这保证了树的高度相对较低,从而提高了搜索、插入和删除操作的效率。
二、平衡因子
平衡因子(Balance Factor,BF)是AVL树中的一个重要概念,用于衡量节点的左右子树的高度差。平衡因子的值只能是-1、0或1。具体计算方式为:节点的右子树高度减去左子树高度。
三、基本操作
AVL树的基本操作包括插入、删除和查找,这些操作都需要在保持树平衡的前提下进行。
-
插入:
- 按照二叉查找树的方式插入新节点。
- 插入后,从插入点向上回溯,更新每个节点的平衡因子。
- 如果发现某个节点的平衡因子绝对值超过1,则进行旋转操作以恢复平衡。
-
删除:
- 找到要删除的节点,并将其向下旋转成一个叶子节点。
- 直接删除该叶子节点。
- 从删除点向上回溯,更新每个节点的平衡因子。
- 如果发现某个节点的平衡因子绝对值超过1,则进行旋转操作以恢复平衡。
-
查找:
- 在AVL树中查找元素的过程与在二叉查找树中相同。
- 由于AVL树总是保持平衡的,所以查找操作的时间复杂度为O(log n)。
四、旋转操作
旋转操作是AVL树保持平衡的关键。根据节点插入或删除后不平衡的具体情况,AVL树的旋转可以分为四种类型:
- 单向右旋(LL):当在节点的左子树的左子树上插入新节点导致节点不平衡(平衡因子为2)时,进行右旋转操作。
- 单向左旋(RR):当在节点的右子树的右子树上插入新节点导致节点不平衡(平衡因子为-2)时,进行左旋转操作。
- 双向旋转(先左后右,LR):当在节点的左子树的右子树上插入新节点导致节点不平衡(平衡因子为2)时,先进行左旋转再进行右旋转。
- 双向旋转(先右后左,RL):当在节点的右子树的左子树上插入新节点导致节点不平衡(平衡因子为-2)时,先进行右旋转再进行左旋转。
五、应用场景
AVL树适用于插入删除次数较少但查找频繁的场景。例如,Windows进程地址空间管理就采用了AVL树来实现高效的查找操作。然而,由于AVL树在插入和删除操作后需要进行复杂的旋转操作来保持平衡,所以其性能在插入和删除操作频繁的场景下可能不如其他数据结构(如红黑树)。
综上所述,AVL树是一种高效的自平衡二叉查找树,通过引入平衡因子和旋转操作来保持树的平衡性,从而提高了搜索、插入和删除操作的效率。
Java代码实现
下面是一个简单的AVL树在Java中的实现。这个实现包括了插入、删除和查找操作,以及必要的旋转操作来维持树的平衡。
class AVLTree {private class Node {int key, height;Node left, right;Node(int d) {key = d;height = 1;}}private Node root;// Utility function to get the height of the treeint height(Node N) {if (N == null)return 0;return N.height;}// Utility function to get the maximum of two integersint max(int a, int b) {return (a > b) ? a : b;}// Right rotate subtree rooted with yNode rightRotate(Node y) {Node x = y.left;Node T2 = x.right;// Perform rotationx.right = y;y.left = T2;// Update heightsy.height = max(height(y.left), height(y.right)) + 1;x.height = max(height(x.left), height(x.right)) + 1;// Return new rootreturn x;}// Left rotate subtree rooted with xNode leftRotate(Node x) {Node y = x.right;Node T2 = y.left;// Perform rotationy.left = x;x.right = T2;// Update heightsx.height = max(height(x.left), height(x.right)) + 1;y.height = max(height(y.left), height(y.right)) + 1;// Return new rootreturn y;}// Get Balance factor of node Nint getBalance(Node N) {if (N == null)return 0;return height(N.left) - height(N.right);}// Insert a node with given key in the subtree rooted with node and returns the new root of the subtreeNode insert(Node node, int key) {// Perform the normal BST insertionif (node == null)return (new Node(key));if (key < node.key)node.left = insert(node.left, key);else if (key > node.key)node.right = insert(node.right, key);else // Duplicate keys are not allowed in BSTreturn node;// Update height of this ancestor nodenode.height = 1 + max(height(node.left), height(node.right));// Get the balance factor of this ancestor node to check whether this node became unbalancedint balance = getBalance(node);// If this node becomes unbalanced, then there are 4 cases// Left Left Caseif (balance > 1 && key < node.left.key)return rightRotate(node);// Right Right Caseif (balance < -1 && key > node.right.key)return leftRotate(node);// Left Right Caseif (balance > 1 && key > node.left.key) {node.left = leftRotate(node.left);return rightRotate(node);}// Right Left Caseif (balance < -1 && key < node.right.key) {node.right = rightRotate(node.right);return leftRotate(node);}// Return the (unchanged) node pointerreturn node;}// Delete a node with given key in the subtree rooted with node and returns the new root of the subtreeNode deleteNode(Node root, int key) {// Perform standard BST deleteif (root == null)return root;if (key < root.key)root.left = deleteNode(root.left, key);else if (key > root.key)root.right = deleteNode(root.right, key);else {// node with only one child or no childif ((root.left == null) || (root.right == null)) {Node temp = null;if (temp == root.left)temp = root.right;elsetemp = root.left;// No child caseif (temp == null) {temp = root;root = null;} else // One child caseroot = temp; // Copy the contents of the non-empty child} else {// node with two children: Get the inorder successor (smallest in the right subtree)Node temp = minValueNode(root.right);// Copy the inorder successor's data to this noderoot.key = temp.key;// Delete the inorder successorroot.right = deleteNode(root.right, temp.key);}}// If the tree had only one node then returnif (root == null)return root;// Update height of the current noderoot.height = max(height(root.left), height(root.right)) + 1;// Get the balance factor of this node (to check whether this node became unbalanced)int balance = getBalance(root);// If this node becomes unbalanced, then there are 4 cases// Left Left Caseif (balance > 1 && getBalance(root.left) >= 0)return rightRotate(root);// Left Right Caseif (balance > 1 && getBalance(root.left) < 0) {root.left = leftRotate(root.left);return rightRotate(root);}// Right Right Caseif (balance < -1 && getBalance(root.right) <= 0)return leftRotate(root);// Right Left Caseif (balance < -1 && getBalance(root.right) > 0) {root.right = rightRotate(root.right);return leftRotate(root);}return root;}Node minValueNode(Node node) {Node current = node;// Loop down to find the leftmost leafwhile (current.left != null)current = current.left;return current;}// A utility function to do inorder traversal of BSTvoid inorder(Node root) {if (root != null) {inorder(root.left);System.out.print(root.key + " ");inorder(root.right);}}// Main functionpublic static void main(String[] args) {AVLTree tree = new AVLTree();/* Constructing tree given in the above figure */tree.root = tree.insert(tree.root, 10);tree.root = tree.insert(tree.root, 20);tree.root = tree.insert(tree.root, 30);tree.root = tree.insert(tree.root, 40);tree.root = tree.insert(tree.root, 50);tree.root = tree.insert(tree.root, 25);/* The constructed AVL Tree would be30/ \20 40/ \ \10 25 50*/System.out.println("Inorder traversal of the constructed AVL tree is:");tree.inorder(tree.root);System.out.println("\n\nDelete 20");tree.root = tree.deleteNode(tree.root, 20);System.out.println("Inorder traversal of the modified tree is:");tree.inorder(tree.root);System.out.println("\n\nDelete 30");tree.root = tree.deleteNode(tree.root, 30);System.out.println("Inorder traversal of the modified tree is:");tree.inorder(tree.root);System.out.println("\n\nDelete 50");tree.root = tree.deleteNode(tree.root, 50);System.out.println("Inorder traversal of the modified tree is:");tree.inorder(tree
相关文章:

每日学习一个数据结构-AVL树
文章目录 概述一、定义与特性二、平衡因子三、基本操作四、旋转操作五、应用场景 Java代码实现 概述 AVL树是一种自平衡的二叉查找树,由两位俄罗斯数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明。想了解树的相关概念,请点击这里。以下是对AVL树的…...
课堂点名系统小程序的设计
管理员账户功能包括:系统首页,个人中心,管理员管理,论坛信息管理,基础数据管理,课程信息管理,课程考勤管理,轮播图信息 微信端账号功能包括:系统首页,论坛信…...
使用Python查找WeChat和QQ的安装路径和文档路径
在日常工作和生活中,我们经常需要查找某些应用程序的安装位置或者它们存储文件的位置。特别是对于像WeChat(微信)和QQ这样的即时通讯软件,了解它们的文件存储位置可以帮助我们更好地管理我们的聊天记录和共享文件。今天࿰…...

【AI大模型】深入Transformer架构:编码器部分的实现与解析(下)
目录 🍔 编码器介绍 🍔 前馈全连接层 2.1 前馈全连接层 2.2 前馈全连接层的代码分析 2.3 前馈全连接层总结 🍔 规范化层 3.1 规范化层的作用 3.2 规范化层的代码实现 3.3 规范化层总结 🍔 子层连接结构 4.1 子层连接结…...

【数据结构】【栈】算法汇总
一、顺序栈的操作 1.准备工作 #define STACK_INIT_SIZE 100 #define STACKINCREMENT 10 typedef struct{SElemType*base;SElemType*top;int stacksize; }SqStack; 2.栈的初始化 Status InitStack(SqStack &S){S.base(SElemType*)malloc(MAXSIZE*sizeof(SElemType));if(…...

如何训练自己的大模型,答案就在这里。
训练自己的AI大模型是一个复杂且资源密集型的任务,涉及多个详细步骤、数据集需求以及计算资源要求。以下是根据搜索结果提供的概述: 详细步骤 \1. 设定目标: - 首先需要明确模型的应用场景和目标,比如是进行分类、回归、生成文本…...

React18新特性
React 18新特性详解如下: 并发渲染(Concurrent Rendering): React 18引入了并发渲染特性,允许React在等待异步操作(如数据获取)时暂停和恢复渲染,从而提供更平滑的用户体验。 通过时…...

汽车发动机系统EMS详细解析
汽车发动机系统EMS,全称Engine-Management-System(发动机管理系统),是现代汽车电子控制技术的重要组成部分。以下是对汽车发动机系统EMS的详细解析,涵盖其定义、工作原理、主要组成、功能特点、技术发展以及市场应用等…...
【社保通-注册安全分析报告-滑动验证加载不正常导致安全隐患】
前言 由于网站注册入口容易被黑客攻击,存在如下安全问题: 暴力破解密码,造成用户信息泄露短信盗刷的安全问题,影响业务及导致用户投诉带来经济损失,尤其是后付费客户,风险巨大,造成亏损无底洞…...

初学Vue(2)
文章目录 监视属性 watch深度监视computed 和 watch 之间的区别 绑定样式(class style)条件渲染列表渲染基本列表key的原理列表过滤列表排序收集表单中的数据 v-model过滤器(Vue3已移除) 监视属性 watch 当被监视的属性变化时&am…...

ThinkPHP5基础入门
文章目录 ThinkPHP5基础入门一、引言二、环境搭建1、前期准备2、目录结构 三、快速上手1、创建模块2、编写控制器3、编写视图4、编写模型 四、调试与部署1、调试模式2、关闭调试模式3、隐藏入口文件 五、总结 ThinkPHP5基础入门 一、引言 ThinkPHP5 是一个基于 MVC 和面向对象…...

Metal 之旅之MTLLibrary
什么是MSL? MSL是Metal Shading Language 的简称,为了更好的在GPU执行程序,苹果公司定义了一套类C的语言(Metal Shading Language ),在GPU运行的程序都是用这个语言来编写的。 什么是MTLLibrary? .metal后缀的文件…...
)
第十二章 Redis短信登录实战(基于Session)
目录 一、User类 二、ThreadLocal类 三、用户业务逻辑接口 四、用户业务逻辑接口实现类 五、用户控制层 六、用户登录拦截器 七、拦截器配置类 八、隐藏敏感信息的代码调整 完整的项目资源共享地址,当中包含了代码、资源文件以及Nginx(Wi…...

华为OD机试 - 九宫格游戏(Python/JS/C/C++ 2024 E卷 100分)
华为OD机试 2024E卷题库疯狂收录中,刷题点这里 专栏导读 本专栏收录于《华为OD机试真题(Python/JS/C/C)》。 刷的越多,抽中的概率越大,私信哪吒,备注华为OD,加入华为OD刷题交流群,…...
详解)
Pytorch库中torch.normal()详解
torch.normal()用法 torch.normal()函数,用于生成符合正态分布(高斯分布)的随机数。在 PyTorch 中,这个函数通常用于生成 Tensor。 该函数共有四个方法: overload def normal(mean: Tensor, std: Tensor, *, generat…...
atcoder-374(a-e)
atcoder-374 文章目录 atcoder-374ABC简洁的写法正解 D正解 E A #include<bits/stdc.h>using namespace std;signed main() {string s;cin>>s;string strs.substr(s.size()-3);if(str "san") puts("Yes");else puts("No");return 0…...
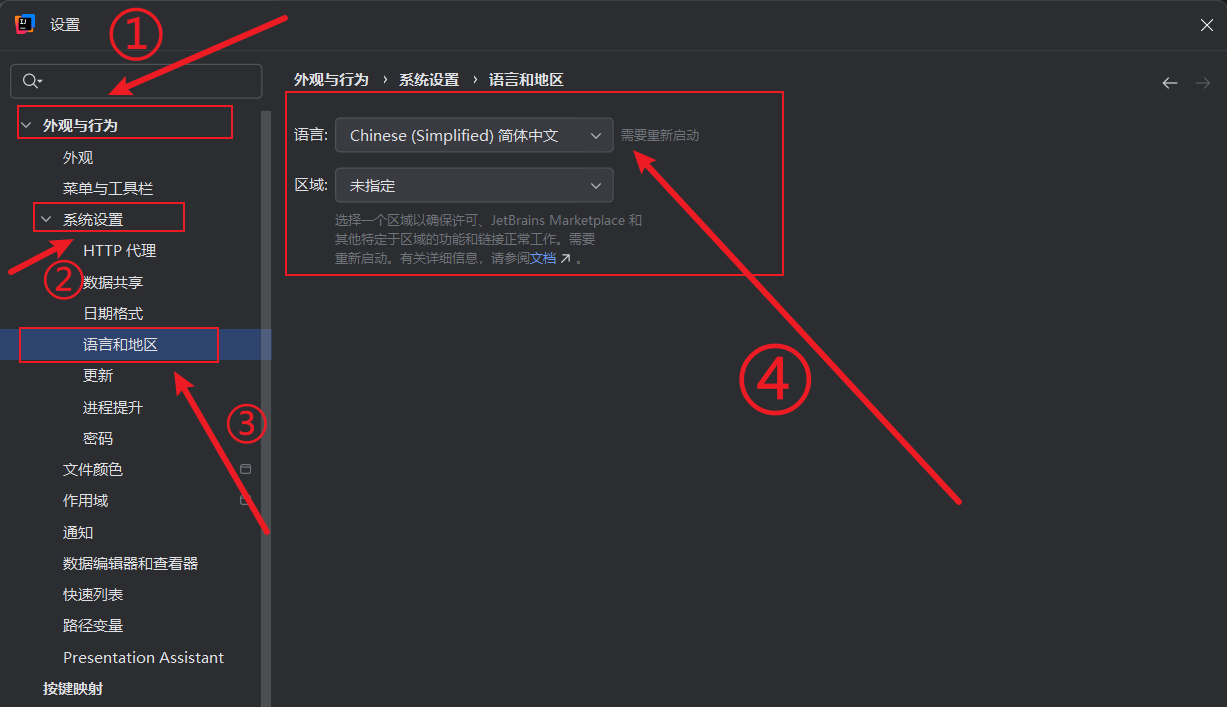
idea2024设置中文
今天下载idea2024.2版本,发现已经装过中文插件,但是还是不显示中文,找了半天原来还需要设置中文选项 方案一 点击文件 -> 关闭项目 点击自定义 -> 选择语言 方案二 点击文件 -> 设置 外观与行为 -> 系统设置 -> 语言和地区…...

跨境电商独立站轮询收款问题
想必做跨境电商独立站的小伙伴,对于PayPal是再熟悉不过了,PayPal是一个跨国际贸易的支付平台,对于做独立站的朋友来说跨境收款绝大部分都是依赖PayPal以及Stripe条纹了。简单来说PayPal跟国内的支付宝有点类似,但是PayPal它是跨国…...

[OS] 3.Insert and Remove Kernel Module
Insert and Remove Kernel Module 1. 切换到 root 账户 $ sudo su作用:Linux 内核模块的加载和卸载需要超级用户权限,因此你必须以 root 用户身份进行操作。sudo su 命令允许你从普通用户切换到 root 账户,从而获得系统的最高权限ÿ…...

updatedb命令:更新locate数据库
一、命令简介 updatedb 命令用于更新 locate 命令使用的文件数据库,以便 locate 命令能够快速定位文件。 二、命令参数 命令格式 updatedb [选项]选项 -l: 仅更新本地文件系统(默认行为)-U: 更新所有文件系统-o D…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

【iOS】 Block再学习
iOS Block再学习 文章目录 iOS Block再学习前言Block的三种类型__ NSGlobalBlock____ NSMallocBlock____ NSStackBlock__小结 Block底层分析Block的结构捕获自由变量捕获全局(静态)变量捕获静态变量__block修饰符forwarding指针 Block的copy时机block作为函数返回值将block赋给…...
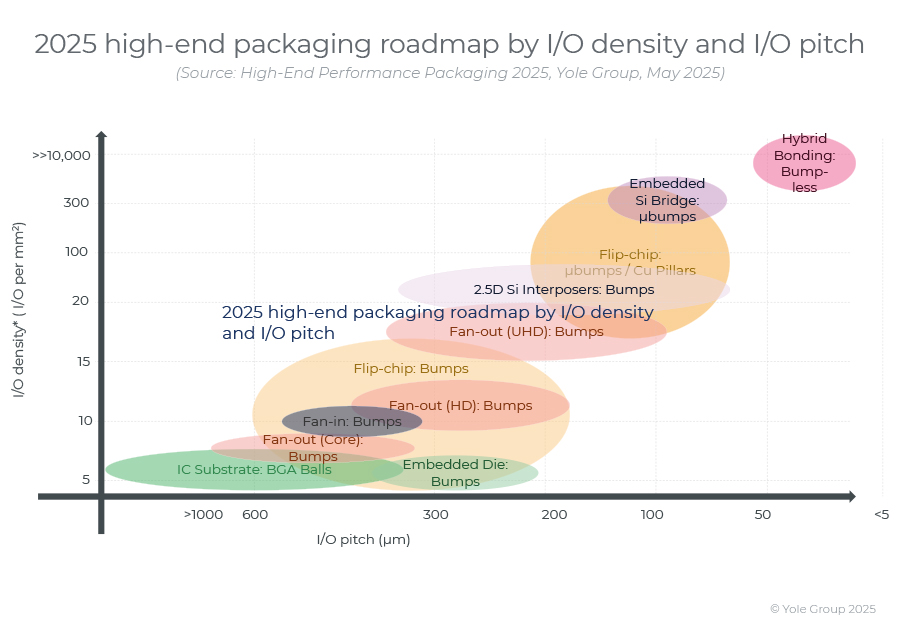
高端性能封装正在突破性能壁垒,其芯片集成技术助力人工智能革命。
2024 年,高端封装市场规模为 80 亿美元,预计到 2030 年将超过 280 亿美元,2024-2030 年复合年增长率为 23%。 细分到各个终端市场,最大的高端性能封装市场是“电信和基础设施”,2024 年该市场创造了超过 67% 的收入。…...

PostgreSQL 与 SQL 基础:为 Fast API 打下数据基础
在构建任何动态、数据驱动的Web API时,一个稳定高效的数据存储方案是不可或缺的。对于使用Python FastAPI的开发者来说,深入理解关系型数据库的工作原理、掌握SQL这门与数据库“对话”的语言,以及学会如何在Python中操作数据库,是…...
)
Spring Boot 与 Kafka 的深度集成实践(二)
3. 生产者实现 3.1 生产者配置 在 Spring Boot 项目中,配置 Kafka 生产者主要是配置生产者工厂(ProducerFactory)和 KafkaTemplate 。生产者工厂负责创建 Kafka 生产者实例,而 KafkaTemplate 则是用于发送消息的核心组件&#x…...

组合模式:构建树形结构的艺术
引言:处理复杂对象结构的挑战 在软件开发中,我们常遇到需要处理部分-整体层次结构的场景: 文件系统中的文件与文件夹GUI中的容器与组件组织结构中的部门与员工菜单系统中的子菜单与菜单项组合模式正是为解决这类问题而生的设计模式。它允许我们将对象组合成树形结构来表示&…...
