如何使用ipopt进行非线性约束求目标函数最小值(NLP非线性规划)内点法(inner point method)
非线性规划,一般用matlab调用cplex和gurobi了,但这两个一般用于线性规划和二次规划
线性规划LP,二次规划(quadratic programming),如果要求更一般的非线性规划IPOT是个很好的选择,求解器很多,根据情况自己选择
非线性

具体的,这篇文章介绍的很清楚了https://blog.csdn.net/mpt0816/article/details/127638557
我这里就是再选择一个问题进行求解
ipopt的可执行程序下载下来, Releases · coin-or/Ipopt · GitHub
建立一个vs2022的工程,把include加到目录里面,把lib库都加进去,同样dll也准备好
就这一个主文件放入工程
编译运行即可
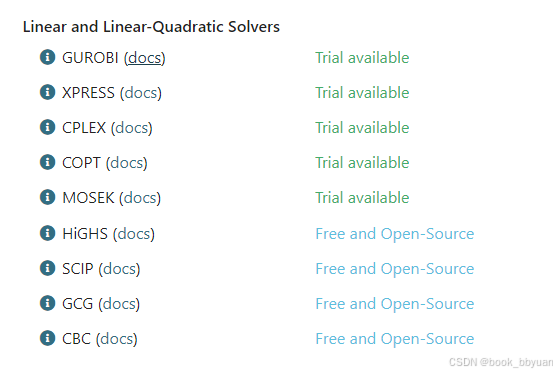
四个自变量,两个约束
eval_f: 计算目标函数值,即需要最小化的目标。
eval_grad_f: 计算目标函数的梯度。分别是4个偏导数
eval_g: 计算约束条件的值。 n 是变量个数,m是约束条件个数,g是具体的约束函数
eval_jac_g: 计算约束条件的雅可比矩阵(两个约束条件的一阶偏导数)
eval_h: 计算目标函数和约束条件的二阶导数(即Hessian矩阵,二阶偏导数)。
现在使用matlab符号函数把 涉及到 用的 梯度、黑森矩阵都求一下
%clear all
close all
clc% 使用符号函数进行 求解梯度,黑森矩阵syms f g1 g2
syms x1 x2 x3 x4% 定义目标函数
f = x1 * x4 * (x1 + x2 + x3) + x3;% 定义约束函数
g1 = x1 * x2 * x3 * x4;
g2 = x1^2 + x2^2 + x3^2 + x4^2;% 计算目标函数的梯度和 Hessian
grad_f = gradient(f, [x1, x2, x3, x4]);
hess_f = hessian(f, [x1, x2, x3, x4]);% 计算约束函数 g1 的梯度和 Hessian
grad_g1 = gradient(g1, [x1, x2, x3, x4]);
hess_g1 = hessian(g1, [x1, x2, x3, x4]);% 计算约束函数 g2 的梯度和 Hessian
grad_g2 = gradient(g2, [x1, x2, x3, x4]);
hess_g2 = hessian(g2, [x1, x2, x3, x4]);得到如下结果:
目标函数 f 的梯度:
x1*x4 + x4*(x1 + x2 + x3)
x1*x4
x1*x4 + 1
x1*(x1 + x2 + x3)
目标函数 f 的 Hessian:
[ 2*x4, x4, x4, 2*x1 + x2 + x3]
[ x4, 0, 0, x1]
[ x4, 0, 0, x1]
[ 2*x1 + x2 + x3, x1, x1, 0]
约束函数 g1 的梯度:
x2*x3*x4
x1*x3*x4
x1*x2*x4
x1*x2*x3
约束函数 g2 的梯度:
2*x1
2*x2
2*x3
2*x4
从g1 g2看出来
nele_jac = 8; 8个非零,两个约束条件,4个变量
nele_hess = 10; 4*5/2=10,看其中一个hess矩阵的上三角阵
约束函数 g1 的 Hessian:
[ 0, x3*x4, x2*x4, x2*x3]
[ x3*x4, 0, x1*x4, x1*x3]
[ x2*x4, x1*x4, 0, x1*x2]
[ x2*x3, x1*x3, x1*x2, 0]
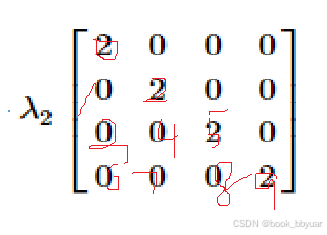
约束函数 g2 的 Hessian:
[ 2, 0, 0, 0]
[ 0, 2, 0, 0]
[ 0, 0, 2, 0]
[ 0, 0, 0, 2]
要替换的部分
1、eval_f 中 目标函数
![]()
2、eval_grad_f 中的梯度
grad_f[0] = x[0] * x[3] + x[3] * (x[0] + x[1] + x[2]);
grad_f[1] = x[0] * x[3];
grad_f[2] = x[0] * x[3] + 1;
grad_f[3] = x[0] * (x[0] + x[1] + x[2]);
3、eval_g 约束条件
g[0] = x[0] * x[1] * x[2] * x[3] + my_data->g_offset[0];
g[1] = x[0] * x[0] + x[1] * x[1] + x[2] * x[2] + x[3] * x[3] + my_data->g_offset[1];
4、eval_jac_g 约束函数的jacobi矩阵
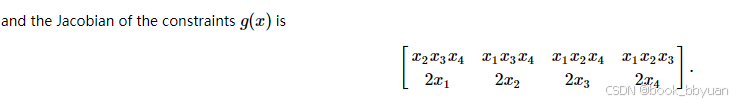
if中 (8个),位置是
00 01 02 03
10 11 12 13,
else 中
g1梯度,g2梯度

5、eval_h 黑森矩阵
固定抄写,4是变量个数
目标的黑森矩阵,注意走位,注意骚走位,注意下三角阵骚走位


约束的黑森
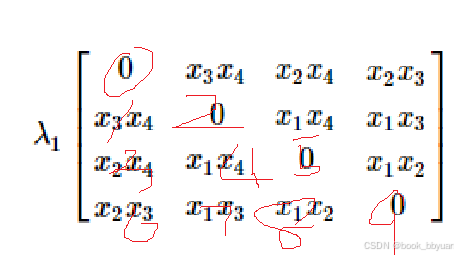

6、主函数
初始值和 上下限
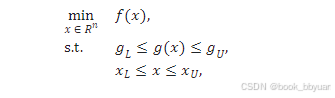

约束条件的jacobi矩阵和hess矩阵的非零元素

8个=2*自变量个数
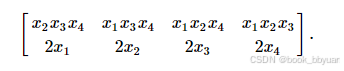
10个=自变量个数*(自变量个数+1)/2

初始值

matlab符号函求解出来的各种算式写成c有点麻烦,我这边搞了一个函数可以很方便转c
function f_str = changetoc(f)syms x1 x2 x3 x4 %替换c语言风格
syms R %为了 R^2也能转% f = x1^2 + x2^2 + x3^2 + x4^2; % 示例符号函数
% f = x1^2 + x2^2 + (x1 + x2)^2 + x3^2 + x4^2; % 示例符号函数,包含复杂表达式
% f = (r*sin(theta)*(3*cos(x1) - 4) + (x2*cos(theta)*(2*cos(x1) - 2))/n1 + (x2*sin(theta)*sin(x1))/n1)^2% 将符号函数转换为字符串
f_str = char(f);% 替换变量为 C 风格的数组索引 x[0], x[1], x[2], x[3]
f_str = regexprep(f_str, 'x1', 'x[0]');
f_str = regexprep(f_str, 'x2', 'x[1]');
f_str = regexprep(f_str, 'x3', 'x[2]');
f_str = regexprep(f_str, 'x4', 'x[3]');% 定义一个集合(Cell数组)用于保存普通变量名
variables = {'x[0]','x[1]','x[2]','x[3]', 'R'};%
% % 示例复杂表达式
% f = (r*sin(theta)*(3*cos(x1) - 4) + (x2*cos(theta)*(2*cos(x1) - 2))/n1 + (x2*sin(theta)*sin(x1))/n1)^2 - R^2 + ...
% (r*cos(theta) + r*sin(theta)*(6*x1 - 6*sin(x1)) + (x2*sin(theta)*(2*cos(x1) - 2))/n1 + ...
% (x2*cos(theta)*(3*x1 - 4*sin(x1)))/n1)^2;% 将符号函数转换为字符串
% f_str = char(f);% 1. 替换普通变量的平方为自乘形式
for i = 1:length(variables)% 构建正则表达式,匹配形如 x1^2, x2^2 等var_pattern = strcat(variables{i}, '^2');% 构建替换字符串 (x1*x1), (x2*x2)replacement = strcat('(', variables{i}, '*', variables{i}, ')');% 进行替换f_str = strrep(f_str, var_pattern, replacement);
end% % 找到 x[i]^2 形式的幂运算,并替换为 (x[i]*x[i])
f_str = regexprep(f_str, '(\w+\[\d+\])\^2', '$1*$1');% 2. 替换括号表达式的平方为自乘形式
% 匹配 (xxxx)^2,替换为 (xxxx)*(xxxx)
% f_str = regexprep(f_str, '\(([^\)]+)\)\^2', '($1)*($1)');
f_str = regexprep(f_str, '\((.*?)\)\^2', '($1)*($1)');% 输出替换后的表达式
disp(f_str);end相关文章:

如何使用ipopt进行非线性约束求目标函数最小值(NLP非线性规划)内点法(inner point method)
非线性规划,一般用matlab调用cplex和gurobi了,但这两个一般用于线性规划和二次规划 线性规划LP,二次规划(quadratic programming),如果要求更一般的非线性规划IPOT是个很好的选择,求解器很多&a…...

【Unity学习笔记】解决疑似升级Win11或使用Unity6导致Unity旧版本无法打开的问题
【Unity学习笔记】解决疑似升级Win11或使用Unity6导致Unity旧版本无法打开的问题 一句话省流: 确保项目地址没有任何中文,重新申请个许可证,然后该咋就咋,完事。 ——————————————————————————————…...

回归分析在数据挖掘中的应用简析
一、引言 在数据驱动的时代,数据挖掘技术已成为从海量数据中提取有价值信息的关键工具。 回归分析,作为一种经典的统计学习方法,不仅在理论研究上有着深厚的基础,而且在实际 应用中也展现出强大的功能。 二、回归分析基础 2.1 回…...

【Node.js】worker_threads 多线程
Node.js 中的 worker_threads 模块 worker_threads 模块是 Node.js 中用于创建多线程处理的工具。 尽管 JavaScript 是单线程的,但有时候在处理计算密集型任务或长时间运行的操作时,单线程的运行会导致主线程被阻塞,影响服务器性能。 为了…...

贪心算法c++
贪心算法C概述 一、贪心算法的基本概念 贪心算法(Greedy Algorithm),又名贪婪法,是一种解决优化问题的常用算法。其基本思想是在问题的每个决策阶段,都选择当前看起来最优的选择,即贪心地做出局部最优的决…...

【STM32】 TCP/IP通信协议(3)--LwIP网络接口
LwIP协议栈支持多种不同的网络接口(网卡),由于网卡是直接跟硬件平台打交道,硬件不同则处理也是不同。那Iwip如何兼容这些不同的网卡呢? LwIP提供统一的接口,底层函数需要用户自行完成,例如网卡的…...

15分钟学 Python 第39天:Python 爬虫入门(五)
Day 39:Python 爬虫入门数据存储概述 在进行网页爬虫时,抓取到的数据需要存储以供后续分析和使用。常见的存储方式包括但不限于: 文件存储(如文本文件、CSV、JSON)数据库存储(如SQLite、MySQL、MongoDB&a…...

使用Pytorch构建自定义层并在模型中使用
使用Pytorch构建自定义层并在模型中使用 继承自nn.Module类,自定义名称为NoisyLinear的线性层,并在新模型定义过程中使用该自定义层。完整代码可以在jupyter nbviewer中在线访问。 import torch import torch.nn as nn from torch.utils.data import T…...
:从前序与中序遍历序列构造二叉树)
学习记录:js算法(五十六):从前序与中序遍历序列构造二叉树
文章目录 从前序与中序遍历序列构造二叉树我的思路网上思路 总结 从前序与中序遍历序列构造二叉树 给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。 示…...

qt使用QDomDocument读写xml文件
在使用QDomDocument读写xml之前需要在工程文件添加: QT xml 1.生成xml文件 void createXml(QString xmlName) {QFile file(xmlName);if (!file.open(QIODevice::WriteOnly | QIODevice::Truncate |QIODevice::Text))return false;QDomDocument doc;QDomProcessin…...

Oracle架构之表空间详解
文章目录 1 表空间介绍1.1 简介1.2 表空间分类1.2.1 SYSTEM 表空间1.2.2 SYSAUX 表空间1.2.3 UNDO 表空间1.2.4 USERS 表空间 1.3 表空间字典与本地管理1.3.1 字典管理表空间(Dictionary Management Tablespace,DMT)1.3.2 本地管理方式的表空…...

springboot整合seata
一、准备 docker部署seata-server 1.5.2参考:docker安装各个组件的命令 二、springboot集成seata 2.1 引入依赖 <dependency><groupId>com.alibaba.cloud</groupId><artifactId>spring-cloud-starter-alibaba-seata</artifactId>&…...
【二次向用户申请授权】程序访问控制)
鸿蒙开发(NEXT/API 12)【二次向用户申请授权】程序访问控制
当应用通过[requestPermissionsFromUser()]拉起弹框[请求用户授权]时,用户拒绝授权。应用将无法再次通过requestPermissionsFromUser拉起弹框,需要用户在系统应用“设置”的界面中,手动授予权限。 在“设置”应用中的路径: 路径…...

docker export/import 和 docker save/load 的区别
Docker export/import 和 docker save/load 都是用于容器和镜像的备份和迁移,但它们有一些关键的区别: docker export/import: export 作用于容器,import 创建镜像导出的是容器的文件系统,不包含镜像的元数据丢失了镜像的层级结构…...

明星周边销售网站开发:SpringBoot技术全解析
1系统概述 1.1 研究背景 如今互联网高速发展,网络遍布全球,通过互联网发布的消息能快而方便的传播到世界每个角落,并且互联网上能传播的信息也很广,比如文字、图片、声音、视频等。从而,这种种好处使得互联网成了信息传…...

STM32+ADC+扫描模式
1 ADC简介 1 ADC(模拟到数字量的桥梁) 2 DAC(数字量到模拟的桥梁),例如:PWM(只有完全导通和断开的状态,无功率损耗的状态) DAC主要用于波形生成(信号发生器和音频解码器) 3 模拟看门狗自动监…...

R语言绘制散点图
散点图是一种在直角坐标系中用数据点直观呈现两个变量之间关系、可检测异常值并探索数据分布的可视化图表。它是一种常用的数据可视化工具,我们通过不同的参数调整和包的使用,可以创建出满足各种需求的散点图。 常用绘制散点图的函数有plot()函数和ggpl…...

安装最新 MySQL 8.0 数据库(教学用)
安装 MySQL 8.0 数据库(教学用) 文章目录 安装 MySQL 8.0 数据库(教学用)前言MySQL历史一、第一步二、下载三、安装四、使用五、语法总结 前言 根据 DB-Engines 网站的数据库流行度排名(2024年)࿰…...
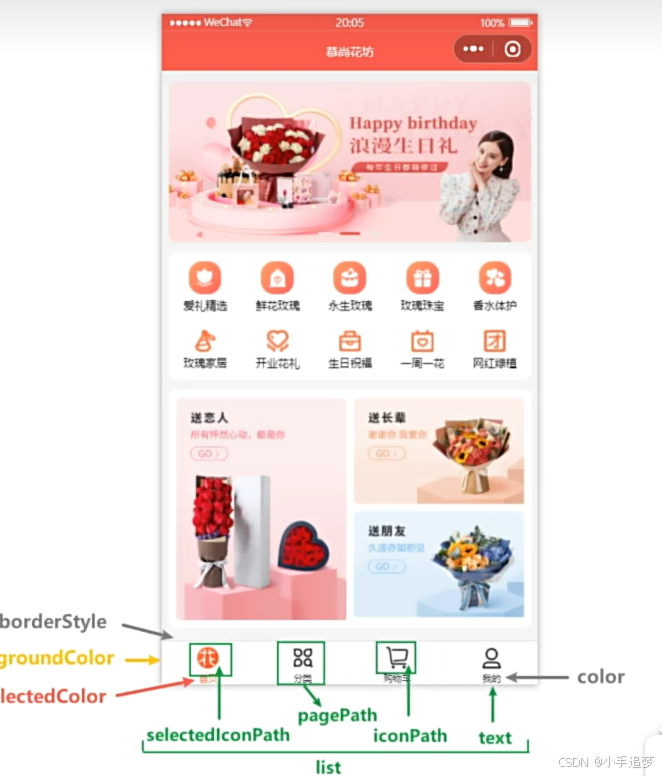
微信小程序开发-配置文件详解
文章目录 一,小程序创建的配置文件介绍二,配置文件-全局配置-pages 配置作用:注意事项:示例: 三,配置文件-全局配置-window 配置示例: 四,配置文件-全局配置-tabbar 配置核心作用&am…...

TCP/UDP初识
TCP是面向连接的、可靠的、基于字节流的传输层协议。 面向连接:一定是一对一连接,不能像 UDP 协议可以一个主机同时向多个主机发送消息 可靠的:无论的网络链路中出现了怎样的链路变化,TCP 都可以保证一个报文一定能够到达接收端…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...
