LeetCode 11 Container with Most Water 解题思路和python代码
题目:
You are given an integer array height of length n. There are n vertical lines drawn such that the two endpoints of the ith line are (i, 0) and (i, height[i]).
Find two lines that together with the x-axis form a container, such that the container contains the most water.
Return the maximum amount of water a container can store.
Notice that you may not slant the container.
Example 1:

Input: height = [1,8,6,2,5,4,8,3,7]
Output: 49
Explanation: The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.
Example 2:
Input: height = [1,1]
Output: 1
Constraints:
n == height.length
2 <= n <= 105
0 <= height[i] <= 104
解题思路:
我们可以看到这里水的体积多少取决于两边的竖直线中较短的那一条。我们可以使用两个指针,一个指向数组的第一个数,另一个指向数组的第二个数。我们可以计算面积,同时移动两个指针中,指向较短竖直线的那一个。
class Solution:def maxArea(self, height: List[int]) -> int:left = 0right = len(height) - 1max_area = 0while left < right:# Calculate the current area width = right - leftcurrent_area = min(height[left], height[right]) * width# Update max_area if the current one is largermax_area = max(max_area, current_area)# Move the pointer that points to the shorter lineif height[left] < height[right]:left += 1else:right -= 1return max_areaTime Complexity 是 O(n)
Space Complexity 是 O(1)
相关文章:

LeetCode 11 Container with Most Water 解题思路和python代码
题目: You are given an integer array height of length n. There are n vertical lines drawn such that the two endpoints of the ith line are (i, 0) and (i, height[i]). Find two lines that together with the x-axis form a container, such that the co…...

【深度学习】损失函数
损失函数(Loss Function)是机器学习和深度学习模型中的一个核心概念,它用于衡量模型的预测输出与真实标签之间的差异。通过优化(最小化)损失函数,模型可以不断调整其内部参数,提升预测性能。不同…...

力扣 中等 46.全排列
文章目录 题目介绍题解 题目介绍 题解 代码如下: class Solution {List<List<Integer>> res new ArrayList<>();// 存放符合条件结果的集合List<Integer> path new ArrayList<>();// 用来存放符合条件结果boolean[] used; // 标记…...
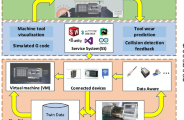
LabVIEW机床加工监控系统
随着制造业的快速发展,机床加工的效率与稳定性成为企业核心竞争力的关键。传统的机床监控方式存在效率低、无法远程监控的问题。为了解决这些问题,开发了一种基于LabVIEW的机床加工监控系统,通过实时监控机床状态,改进生产流程&am…...

第五届智能设计国际会议(ICID 2024)
文章目录 一、会议详情二、重要信息三、大会介绍四、出席嘉宾五、征稿主题六、咨询 一、会议详情 二、重要信息 大会官网:https://ais.cn/u/vEbMBz提交检索:EI Compendex、IEEE Xplore、Scopus大会时间:2024年10月25-27日大会地点࿱…...

厨房用品分割系统源码&数据集分享
厨房用品分割系统源码&数据集分享 [yolov8-seg-C2f-DCNV3&yolov8-seg-AFPN-P345等50全套改进创新点发刊_一键训练教程_Web前端展示] 1.研究背景与意义 项目参考ILSVRC ImageNet Large Scale Visual Recognition Challenge 项目来源AAAI Global Al ln…...

【HTTPS】深入解析 https
我的主页:2的n次方_ 1. 背景介绍 在使用 http 协议的时候是不安全的,可能会出现运营商劫持等安全问题,运营商通过劫持 http 流量,篡改返回的网页内容,例如广告业务,可能会通过 Referer 字段 来统计是…...

Axios 快速入门
什么是Ajax Ajax 是一种通过 JavaScript 发送异步请求的技术,它的核心是使用 XMLHttpRequest 对象来与服务器交换数据。这种方式较为繁琐,因为需要手动处理请求状态和响应,并且编写的代码往往比较冗长。 相较之下,Axios 是一个基于…...
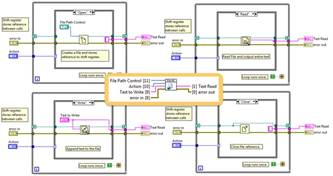
LabVIEW提高开发效率技巧----调度器设计模式
在LabVIEW开发中,针对多任务并行的需求,使用调度器设计模式(Scheduler Pattern)可以有效地管理多个任务,确保它们根据优先级或时间间隔合理执行。这种模式在需要多任务并发执行时特别有用,尤其是在实时系统…...

python之认识变量
1、变量 1.1、定义 字面意思来看,会发生改变的量称为变量。 相反的,如果有一个不会发生改变的量,它应该称为不变量,即常量。 1.2、引入变量的原因 主要是为了方便程序员动态的管理、操控数据。 1.3、变量的三要素 名称 类型…...

c++应用网络编程之十Linux下的Poll模式
一、Poll模式 在上一篇文章中提到了Select模式的缺点。既然有缺点,就要改正。但是直接在Select模式上修改不太现实,那么就推出一个新的模式不更香么?poll模式就应运而生了。不过,罗马不是一天建成的,poll模式也只是对…...

[C++][第三方库][RabbitMq]详细讲解
目录 1.介绍2.安装1.RabbitMq2.客户端库 3.AMQP-CPP 简单使用1.介绍2.使用 4.类与接口1.Channel2.ev 5.使用1.publish.cc2.consume.cc3.makefile 1.介绍 RabbitMQ:消息队列组件,实现两个客户端主机之间消息传输的功能(发布&订阅)核心概念࿱…...

Next.js 详解
Next.js是一个基于React的开源JavaScript框架,由Vercel(原Zeit)公司开发。它旨在简化React应用的构建过程,并提供了一系列强大的功能来优化性能和开发体验。以下是对Next.js的详细解析: 一、核心特性 服务器端渲染&…...

pygame--超级马里奥(万字详细版)
超级马里奥点我下载https://github.com/marblexu/PythonSuperMario 1.游戏介绍 小时候的经典游戏,代码参考了github上的项目Mario-Level-1,使用pygame来实现,从中学习到了横版过关游戏实现中的一些处理方法。原项目实现了超级玛丽的第一个小…...

【运维】nginx静态代理资源403权限问题
如题,遇到静态代理资源访问403,可以尝试检查其文件权限,父目录权限,需要确保 "目录使用标准的 755,对文件使用 644(umask:022)" 参考资料: 1. nginx “403 …...

java家政预约上门系统源码,家政服务平台源码,基于SpringBoot框架,数据库使用MySQL,界面渲染采用Thymeleaf技术开发
自主知识产权的家政预约上门系统源码,java版本,支持二次开发,适合商用上项目。 在这个快节奏的现代生活中,越来越多的家庭开始寻求高效、便捷的家政服务解决方案。传统的家政服务模式已经很难满足人们日益增长的个性化与即时性需求…...

算法知识点————贪心
贪心:只考虑局部最优解,不考虑全部最优解。有时候得不到最优解。 DP:考虑全局最优解。DP的特点:无后效性(正在求解的时候不关心前面的解是怎么求的); 二者都是在求最优解的,都有最优…...

python数据分析
Python是一种非常流行的编程语言,尤其在数据分析领域。Python拥有丰富的库和框架,可以帮助你执行各种数据分析任务。Python常用的数据分析工具之一:NumPy。 Numpy用于进行大规模数值和矩阵运算,提供了多维数组对象和一系列操作这…...

UGUI(现成组合控件)
Drop Down Scroll View Scroll Bar size是滚动条的填充程度 Slider 如果设置为静态,那么传入的值始终为自己设置的那个值 Input Field content type为standard时 可以设置line type, 只读不改,就是可以复制,但是你已经不能输入了…...

软件交付体系文件(Word源资料)
软件文档交付清单是指在软件开发项目完成后,开发团队需要准备的一份详细清单,用于确保交付的软件产品符合客户需求并达到预期的质量标准。以下是软件文档交付清单中可能包含的一些关键要素 软件全套资料部分文档清单: 工作安排任务书…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...
