uniapp中nvue与vue的区别?
文章目录
- 简介
- nvue 和 vue 相互通讯方式:
- nvue注意事项:
简介
uni-app是逻辑渲染分离的,渲染层在app端提供了两套排版引擎,
小程序方式的webview渲染和weex方式的原生渲染,两种渲染引入可以自己根据需要选。
vue文件走的是webview渲染。
nvue走的是wexx方式的原生渲染
组件和js写法是一样的,css不一样,原生排版的能用的css必须是flex布局。
uni-app的app端内置了一个基于wexx改进的原生渲染引擎,提供了原生渲染的能力,在app端,如果一个aap中可以同时使用两种页面,例如:首页使用nvue,二级页面上使用vue页面。
nvue 和 vue 相互通讯方式:
在 uni-app 中,nvue 和 vue 页面可以混搭使用。
推荐使用uni.o n , u n i . on,uni.on,uni.emit的方式进行页面通讯
nvue注意事项:
- nvue 页面均采用 flex 布局,不支持其他布局方式,不能使用百分比。需要注意的是 flex 默认为竖向排列,即 flex-direction: column,如需改变布局方向可以使用flex-direction: row;改变为横排
- 在 App.vue 中定义的全局样式不会在 nvue 页面生效。
- 不能在 style 中引入字体文件,nvue 中字体图标的使用参考:weex 加载自定义字体
- class 进行绑定时只支持数组 语法(weex 限制)
- nvue 页面跳转 vue 页面时,只能调用 uni-app 的 路由 API 进行跳转
- 目前不支持在 nvue 页面使用 s css、less 等预编译语言。
- nvue 中不支持使用 import 的方式引入外部 css 需要使用style中的src方式引入。
- 很多css样式不支持简写,例如border:1px solid black 不支持。
- nvue 页面控制显隐只可以使用v-if不可以使用v-show
- 单位只支持px 不支持em,rem,pt,%,upx
相关文章:

uniapp中nvue与vue的区别?
文章目录简介nvue 和 vue 相互通讯方式:nvue注意事项:简介 uni-app是逻辑渲染分离的,渲染层在app端提供了两套排版引擎, 小程序方式的webview渲染和weex方式的原生渲染,两种渲染引入可以自己根据需要选。 vue文件走的…...

带头双向循环链表的实现
1.结构体的创建以及类型重定义 typedef int LTDataType; typedef struct ListNode {LTDataType data;struct ListNode* prev;struct ListNode* next; }LTNode;2.链表的初始化 这个函数用于创建节点,后面还会用到。 LTNode* BuyListNode(LTDataType x) {LTNode* n…...

大屏使用dv-digital-flop定时刷新显示总人数
本文在基础上进行改进,后端使用若依后端IofTV-Screen: 🔥一个基于 vue、datav、Echart 框架的物联网可视化(大屏展示)模板,提供数据动态刷新渲染、屏幕适应、数据滚动配置,内部图表自由替换、Mixins注入等功…...

Java面向对象部分 个人学习记录
注:此博客是个人学习记录,会有错的地方,面向对象部分我可能会画很多图来加深我的理解 不引出了,直接开始 class Dog{String name;int age;String type;public Dog(String name,int age,String type){this.namename;this.ageage;this.typetyp…...
MySQL数据库——对Linux MySQL软件包的一些说明
Linux 操作系统的发行版很多,不同发行版下的 MySQL 版本也是不同的。MySQL 主要支持的 Linux 版本有 Red Hat Enterprise Linux 和 SUSE Linux Enterprise Server。这里主要介绍不同 Linux 发行版下 MySQL 支持的版本。 Linux 操作系统的 MySQL 软件包一般分为以下…...

【JavaEE进阶】——第二节.Spring核心和设计思想
文章目录 前言 一、Spring是什么? 二、什么是容器? 三、什么是IoC? 3.1 初始loC 3.2 举例解释loC 3.3 Spring IoC思想的体现 四、什么是DI? 4.1DI的概念 4.2 Ioc和DI的区别 总结 前言 今天我们将进入到有关spring的认识当中&…...
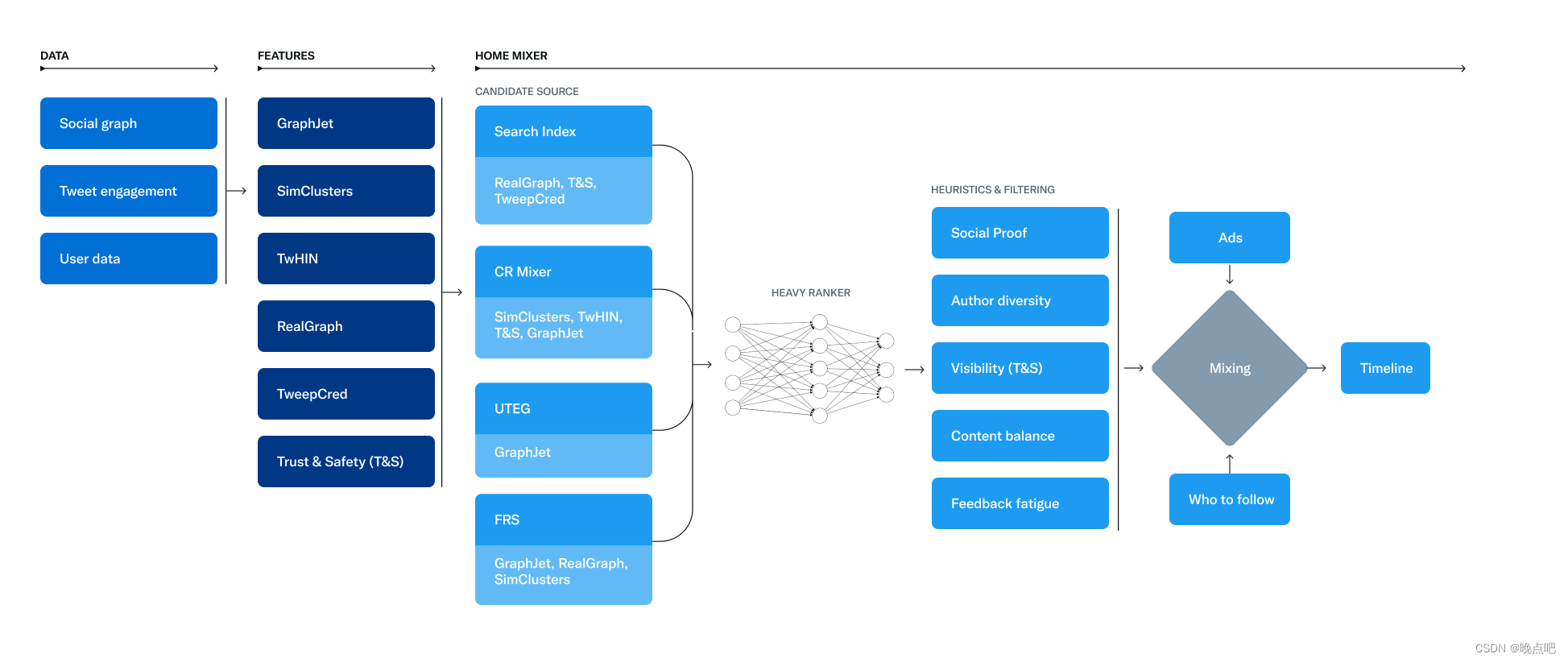
twitter开源算法(1)For You推荐系统架构
1 Twitter’s Recommendation Algorithm 我们的推荐系统由许多互相关联的服务(services)和工作(jobs)组成,本节这要是聚焦home timeline的for you feed流。 the-algorithm开源地址:https://github.com/twitter/the-algorithm 本篇博客来源&…...
)
A General Framework for Uncertainty Estimation in Deep Learning源码阅读(二)
接上文 ResNet定义: 代码使用 def ResNet18ADF(noise_variance1e-3, min_variance1e-3):return ResNet(BasicBlock, [2,2,2,2], num_classes10, noise_variance1e-3, min_variance1e-3, initialize_msraFalse)定义模型,其中ResNet定义为: …...

串行通信协议---HART协议
实际应用中,HART协议是仅次于Modbus协议的最接近统一现场总线的标准,主要是在4~20mA电流信号上面叠加数字信号,物理层采用Bell 202标准的FSK技术成功实现模拟信号和数字信号双向同时通信而互不干扰。HART协议规定了传输的物理形式、消息结构、…...
)
【独家】华为OD机试 - 寻找密码(C 语言解题)
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南华为od机试,独家整理 已参加机试人员的实战技巧本期题目:寻找密码 题目 小王在进行游…...

FPGA有哪些优质的带源码的IP开源网站?
这是某乎上的一个问题,我觉得还不错,今天就系统性的总结一下1、fpga4funhttps://www.fpga4fun.com/你能在这个网站上找到什么?您可以找到信息页面,以及使用 FPGA 板构建的 FPGA 项目。注重点:项目。FPGA 项目使用一种称…...
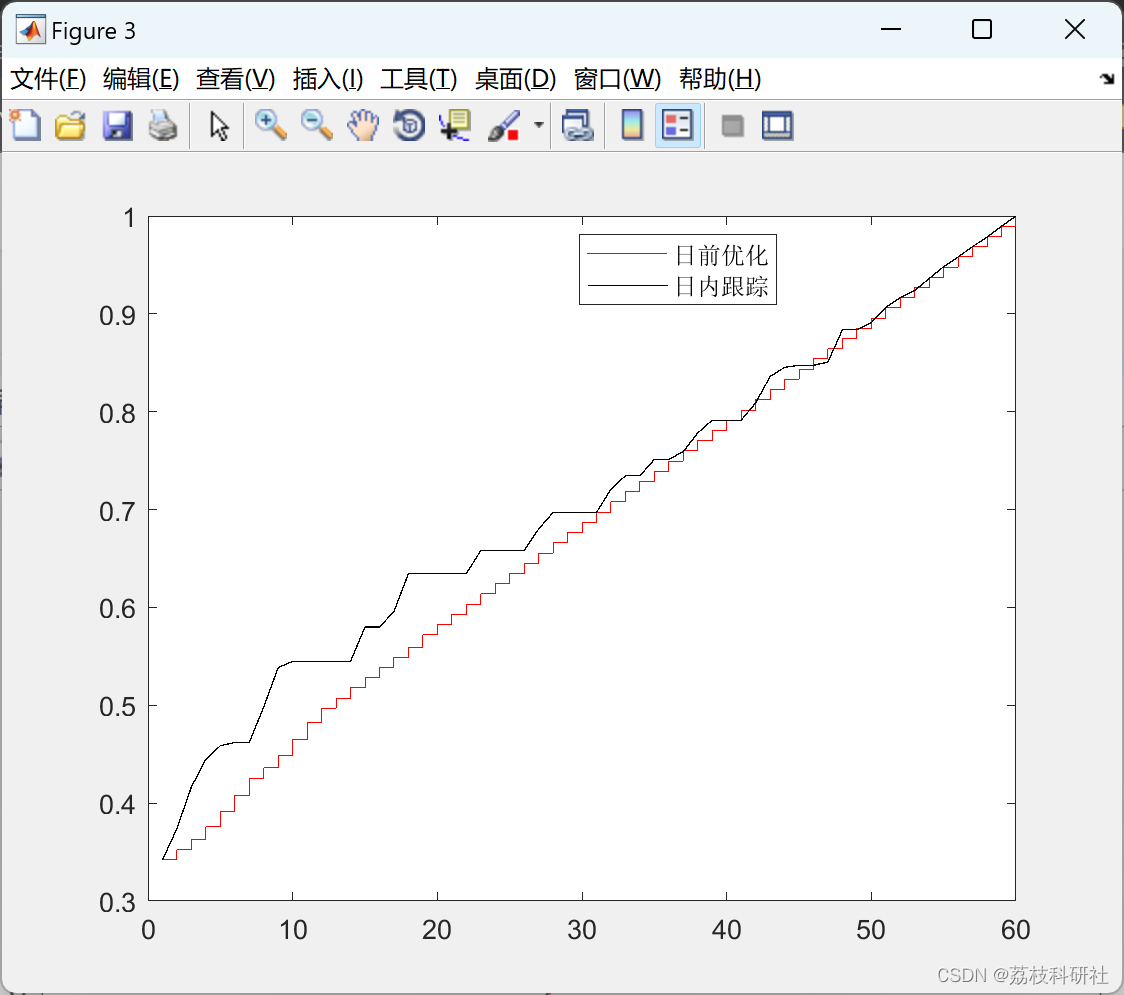
基于模型预测控制(MPC)的微电网调度优化的研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
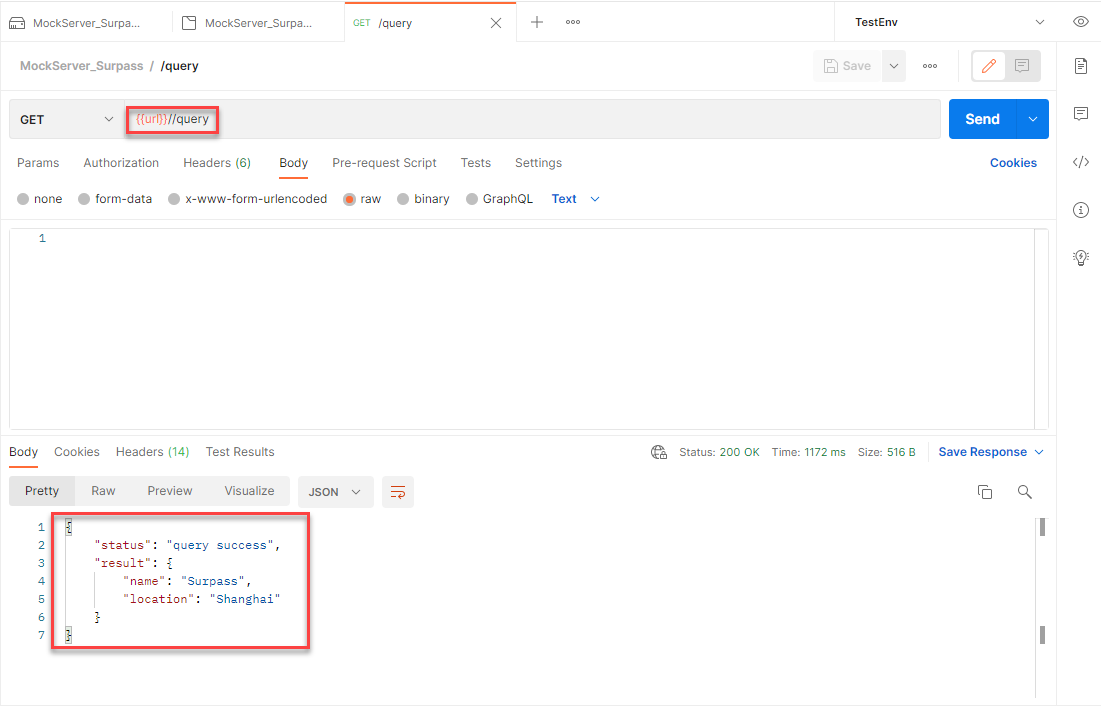
Postman接口测试之Mock快速入门
一、Mock简介 1.Mock定义 Mock是一种比较特殊的测试技巧,可以在没有依赖项的情况下进行接口或单元测试。通常情况下,Mock与其他方法的区别是,用于模拟代码依赖对象,并允许设置对应的期望值。简单一点来讲,就是Mock创建…...

分享一个国内可用的免费ChatGPT网站
背景 ChatGPT作为一种基于人工智能技术的自然语言处理工具,近期的热度直接沸腾🌋。 作为一个程序员,我也忍不住做了一个基于ChatGPT的网站,免费!免登陆!!国内可直接对话ChatGPT,也…...
)
15. 三数之和(Java)
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ,同时还满足 nums[i] nums[j] nums[k] 0 。请 你返回所有和为 0 且不重复的三元组。 注意:答案中不可以包含重复的三元组。 示例 …...

Navicat Premium 16安装教程
1.鼠标右击【Navicat Premium 16(64bit)】压缩包(win11及以上系统需先选择“显示更多选项”)选择【解压到 Navicat Premium 16(64bit)】。 2.打开解压后的文件夹,鼠标右击【setup】选择【以管理员身份运行】。 3.点击【下一步】。 4.选择【我…...

蓝桥杯刷题冲刺 | 倒计时8天
作者:指针不指南吗 专栏:蓝桥杯倒计时冲刺 🐾马上就要蓝桥杯了,最后的这几天尤为重要,不可懈怠哦🐾 文章目录1.三角形的面积2.图中点的层次1.三角形的面积 题目 链接: 三角形的面积 - 蓝桥云课 …...

四.JAVA基础面试题:重要知识
四.JAVA基础面试题:重要知识 1.为什么JAVA只有值传递 2.JAVA获取运行时类的四种方式 四.JAVA基础面试题:重要知识 1.为什么JAVA只有值传递 实参:传递给形参的实际参数。 形参:接受实参的参数。值传递:方法接受实参…...

某面试官分享经验:看求职者第一眼,开口说第一句话,面试结果就差不多定了,准确率高达90%以上...
我们以前分享过许多经验,但大多是站在打工人的视角上,今天给大家带来一个面试官的经验:1. 看求职者第一眼,开口说第一句话,面试结果就差不多定了,准确率高达90%以上。2. 绝不考八股文,如果问技术…...

Java开发 - 消息队列之RabbitMQ初体验
目录 前言 RabbitMQ 什么是RabbitMQ RabbitMQ特点 安装启动 RabbitMQ和Kafka的消息收发区别 RabbitMQ使用案例 添加依赖 添加配置 创建RabbitMQ配置类 RabbitMQ消息的发送 RabbitMQ消息的接收 测试 结语 前言 前一篇,我们学习了Kafka的基本使用&#…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...

【Ftrace 专栏】Ftrace 参考博文
ftrace、perf、bcc、bpftrace、ply、simple_perf的使用Ftrace 基本用法Linux 利用 ftrace 分析内核调用如何利用ftrace精确跟踪特定进程调度信息使用 ftrace 进行追踪延迟Linux-培训笔记-ftracehttps://www.kernel.org/doc/html/v4.18/trace/events.htmlhttps://blog.csdn.net/…...
