【题目解析】蓝桥杯23国赛C++中高级组 - 斗鱼养殖场
【题目解析】蓝桥杯23国赛C++中高级组 - 斗鱼养殖场
题目链接跳转:点击跳转
前置知识:
- 了解过基本的动态规划。
- 熟练掌握二进制的位运算。
题解思路
这是一道典型的状压动态规划问题。设 d p i , j dp_{i, j} dpi,j 表示遍历到第 i i i 行的时候,当前行以 j ( b a s e 2 ) j_{(base2)} j(base2) 的形式排列乌龟可以构成的方案数。
对于每一行的方案,我们可以用一个二进制来表示。例如二进制数字 10100 10100 10100,表示有一个横向长度为 5 5 5 的场地中,第 1 , 3 1, 3 1,3 号位置分别放置了一只小乌龟。因此,每一种摆放状态都可以用一个二进制数字来表示。我们也可以通过遍历的方式来遍历出二进制的每一种摆放状态。
首先,我们预处理出横排所有放置乌龟的合法情况。根据题意,两个乌龟不能相邻放置,因此在二进制中,不能有两个 1 1 1 相邻。如何预处理出这种情况呢?我们可以使用位运算的方法:
如果存在一个二进制数字有两个 1 1 1 相邻,那么如果我们对这个数字 x x x 进行位运算操作 (x << 1) & x 的结果或 (x >> 1) & x 的结果必定大于等于 1 1 1。我们通过把这种情况排除在外。同时,我们还需要注意有些格子中不能放置乌龟。这一步也可以通过二进制的方法预处理掉,如果网箱在第 i i i 一个格子中不能放置乌龟,那么在枚举所有方案数的时候直接忽略掉第 i i i 位为 1 1 1 的情况即可。
接下来如何保证上下两行的乌龟不冲突?假如上一行的摆放状态是 y y y,当前行的摆放状态为 j j j,如果 i & j 的结果大于等于 1 1 1,也可以证明有两个数字 1 1 1 在同一位置上。因此我们也需要把这种情况排除在外。
综上所述,我们可以得出状态转移方程: d p i , j = d p i , j + d p i − 1 , k dp_{i, j} = dp_{i, j} + dp_{i-1, k} dpi,j=dpi,j+dpi−1,k。其中, j j j 和 k k k 表示所有横排合法的方案。答案就是 A N S = ∑ j = 0 2 M − 1 d p N , j \mathtt{ANS} = \sum_{j=0}^{2^M-1}{dp_{N, j}} ANS=∑j=02M−1dpN,j。
状态的初始化也很简单,另 d p 0 , 0 = 1 dp_{0, 0} = 1 dp0,0=1,表示一只乌龟都不放有一种摆放方案。
时间复杂度
通过观察上述代码,在枚举所有状态和转移状态的时候有三层循环,分别是枚举当前行、枚举当前行的合法摆放情况以及枚举上一行的摆放情况。因此总时间复杂度约为 O ( n × 2 M × 2 M ) = O ( n × 2 M 2 ) = O ( n × 4 M ) O(n \times 2^M \times 2^M) = O(n \times 2^{M^2}) = O(n \times 4^M) O(n×2M×2M)=O(n×2M2)=O(n×4M)。但由于合法的摆放数量远远少于 2 M 2^M 2M,因此实际情况下程序运行的速度会快许多。
代码实现
本题的代码实现如下。在输出的时候需要减一,因为不放置也是一种合法情况,根据题目要求需要把这一合法情况排除。
#include <iostream>
using namespace std;const int MOD = 1e9+7;
int n, m, ans;
int arr[505][505];
// 所有横排合法的情况。
int terrain[505];
int ok[1050], cnt;
int dp[505][1050];int main(){cin >> n >> m;for (int i=1; i<=n; i++){for (int j=1; j<=m; j++){cin >> arr[i][j];}}// 预处理非法地形。for (int i=1; i<=n; i++){for (int j=1; j<=m; j++){terrain[i] = (terrain[i] << 1) + !arr[i][j];}}// 预处理出所有横排的合法情况。for (int i=0; i<(1<<m); i++){if (((i<<1)|(i>>1)) & i) continue;ok[++cnt] = i;}dp[0][1] = 1;// 枚举。for (int i=1; i<=n; i++){for (int s1=1; s1<=cnt; s1++){ // 枚举当前行。if (ok[s1] & terrain[i]) continue;for (int s2=1; s2<=cnt; s2++){ // 枚举上一行。if (ok[s2] & terrain[i-1]) continue;if (ok[s1] & ok[s2]) continue;dp[i][s1] = (dp[i][s1] + dp[i-1][s2]) % MOD;}}}// 统计答案。int ans = 0;for (int i=1; i<=cnt; i++)ans = (ans + dp[n][i]) % MOD;cout << ans - 1 << endl;return 0;
}
本题的 Python 代码如下,Python 可以通过本题的所有测试点:
MOD = int(1e9 + 7)
n, m, ans = 0, 0, 0
arr = [[0] * 505 for _ in range(505)]
terrain = [0] * 505
ok = [0] * 1050
dp = [[0] * 1050 for _ in range(505)]
cnt = 0def main():global n, m, cnt, ans# 输入 n 和 mn, m = map(int, input().split())# 输入 arr 数组for i in range(1, n + 1):arr[i][1:m + 1] = map(int, input().split())# 预处理非法地形for i in range(1, n + 1):for j in range(1, m + 1):terrain[i] = (terrain[i] << 1) + (1 - arr[i][j])# 预处理出所有横排的合法情况for i in range(1 << m):if ((i << 1) | (i >> 1)) & i:continuecnt += 1ok[cnt] = idp[0][1] = 1# 枚举for i in range(1, n + 1):for s1 in range(1, cnt + 1): # 枚举当前行if ok[s1] & terrain[i]:continuefor s2 in range(1, cnt + 1): # 枚举上一行if ok[s2] & terrain[i - 1]:continueif ok[s1] & ok[s2]:continuedp[i][s1] = (dp[i][s1] + dp[i - 1][s2]) % MOD# 统计答案ans = 0for i in range(1, cnt + 1):ans = (ans + dp[n][i]) % MODprint(ans - 1)if __name__ == "__main__":main()再提供一个暴力解法用于对拍:
#include <iostream>
using namespace std;const int MOD = 1e9+7;
int n, m, ans;
int arr[505][505];
int dx[] = {0, 1, -1, 0};
int dy[] = {1, 0, 0, -1};// 深度优先搜索 Brute Force
void dfs(int x, int y){if (x > n) {ans += 1;ans %= MOD;return ;}if (y > m){dfs(x+1, 1);return ;}if (arr[x][y] == 0){dfs(x, y+1);return ;}// 不放鱼dfs(x, y+1);// 放鱼for (int i=0; i<4; i++){int cx = x + dx[i];int cy = y + dy[i];if (cx < 1 || cy < 1 || cx > n || cy > m) continue;if (arr[cx][cy] == 2) return ;}arr[x][y] = 2;dfs(x, y+1);arr[x][y] = 1;return ;
}int main(){cin >> n >> m;for (int i=1; i<=n; i++){for (int j=1; j<=m; j++){cin >> arr[i][j];}}// dfs 暴力dfs(1, 1);cout << ans-1 << endl;return 0;
}
相关文章:

【题目解析】蓝桥杯23国赛C++中高级组 - 斗鱼养殖场
【题目解析】蓝桥杯23国赛C中高级组 - 斗鱼养殖场 题目链接跳转:点击跳转 前置知识: 了解过基本的动态规划。熟练掌握二进制的位运算。 题解思路 这是一道典型的状压动态规划问题。设 d p i , j dp_{i, j} dpi,j 表示遍历到第 i i i 行的时候&a…...

JavaScript可视化:探索顶尖的图表库
JavaScript可视化:探索顶尖的图表库 在这个被数据驱动的时代,你有没有想过,数据本身是如何变得有意义的?答案就是数据可视化。通过图表和图形,我们不仅可以看到数据,还可以感受到它,从而做出明…...

谷歌AI大模型Gemini API快速入门及LangChain调用视频教程
1. 谷歌Gemini API KEY获取及AI Studio使用 要使用谷歌Gemini API,首先需要获取API密钥。以下是获取API密钥的步骤: 访问Google AI Studio: 打开浏览器,访问Google AI Studio。使用Google账号登录,若没有账号…...

进入容器:掌控Docker的世界
进入容器:掌控Docker的世界 在这个快速发展的技术时代,你是否曾被Docker的庞大生态所吸引?那么,有没有想过在这个容器化的世界里,如何快速高效地“进入”这些隐藏在虚拟墙后的容器呢?容器就如同魔法箱,装载着应用与服务,而你,通过探索这些容器,能够更好地管理、排除…...

初始Linux(二)基础命令
前言: 之前那一篇我们已经介绍了一部分的基础命令,当然那只不过是九牛一毛,本篇我们继续介绍一些比较重要且需要掌握的基础命令。 mv命令: 其实这个命令有两个功能,一个是移动(剪切)文件&#…...

STM32 OLED
文章目录 前言一、OLED是什么?二、使用步骤1.复制 OLED.C .H文件1.1 遇到问题 2.统一风格3.主函数引用头文件3.1 oled.h 提供了什么函数 4.介绍显示一个字符的函数5. 显示十进制函数的讲解 三、使用注意事项3.1 配置符合自己的引脚3.2 花屏总结 前言 提示ÿ…...
伦敦金实时行情决策辅助!
在伦敦金实时交易的过程中,投资者主要依赖技术分析来辅助自己的投资决策。与基本面分析不同,技术分析侧重于研究金价的走势和市场行为,通过图表和技术指标来预测未来的市场走势。常用的技术分析方法包括: 趋势线和支撑阻力位&…...

Leetcode 746. 使用最小花费爬楼梯 入门dp C++实现
问题:Leetcode 746. 使用最小花费爬楼梯 给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。 你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。 请你…...

路由协议常见知识点
路由协议是网络通信的基础,主要负责在网络中传递数据包,并确保它们从源节点传递到目标节点。本文将介绍一些常见的路由协议知识点,包括路由协议的分类、特性、配置与管理以及常见问题。 一、路由协议的分类 距离矢量路由协议: R…...
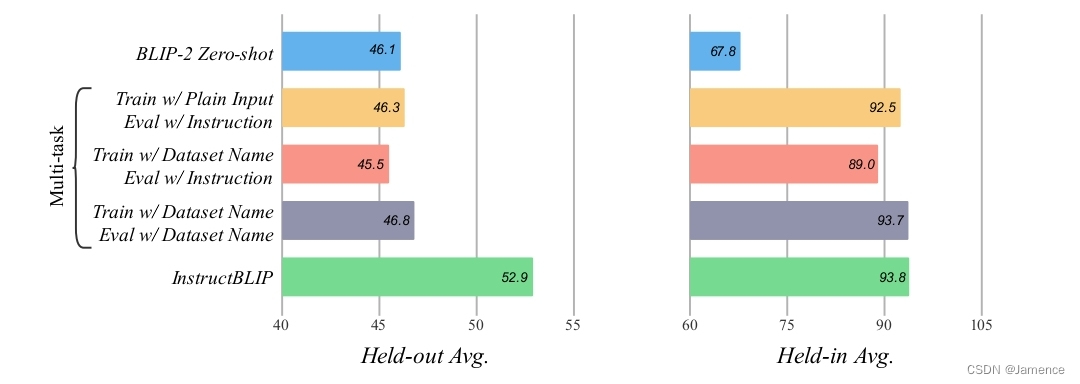
多模态大语言模型(MLLM)-InstructBlip深度解读
前言 InstructBlip可以理解为Blip2的升级版,重点加强了图文对话的能力。 模型结构和Blip2没差别,主要在数据集收集、数据集配比、指令微调等方面下文章。 创新点 数据集收集: 将26个公开数据集转换为指令微调格式,并将它们归类…...
:字符串)
网页前端开发之Javascript入门篇(7/9):字符串
Javascript字符串 什么是字符串? 答:其概念跟 Python教程 介绍的一样,只是语法上有所变化。 在 Javascript 中,一个字符串变量可以看做是其内置类String的一个实例(Javascript会自动包装)。 因此它拥有一…...

双登股份再战IPO:数据打架,实控人杨善基千万元股权激励儿子
撰稿|行星 来源|贝多财经 近日,双登集团股份有限公司(下称“双登股份”)递交招股书,准备在港交所主板上市,中金公司、建银国际、华泰国际为其联席保荐人。 贝多财经了解到,这并非双登股份首次向资本市场…...
)
4.Python 函数(函数的定义、函数的传入参数、函数的返回值、None 类型、函数说明文档、变量的作用域)
一、函数快速入门 1、函数概述 函数是组织好的,可重复使用的,用来实现特定功能的代码段 name "Hello World" name_length len(name)print(f"{name} 的长度为 {name_length}") # Hello World 的长度为 11len() 是Python 内置的函…...

【JavaEE】——文件IO
阿华代码,不是逆风,就是我疯 你们的点赞收藏是我前进最大的动力!! 希望本文内容能够帮助到你!! 目录 一:认识文件 1:文件的概念 2:文件的结构 3:文件路径…...

Python的pandas库基本操作(数据分析)
一、安装,导入 1、安装 使用包管理器安装: pip3 install pandas 2、导入 import pandas as pd as是为了方便引用起的别名 二、DateFrame 在Pandas库中,DataFrame 是一种非常重要的数据结构,它提供了一种灵活的方式来存储和…...
)
软件测试(平铺版本)
目录 黑盒测试: 定义: 示例:登录功能的黑盒测试 适合使用黑盒测试的情况 几种常见的黑盒测试方法: 1. 等价类划分(Equivalence Partitioning) 2. 边界值分析(Boundary Value Analysis) …...

树控件QTreeWidget
树控件跟表格控件类似,也可以有多列,也可以只有1列,可以有多行,只不过每一行都是一个QTreeWidgetItem,每一行都是一个可以展开的树 常用属性和方法 显示和隐藏标题栏 树控件只有水平标题栏 //获取和设置标题栏的显…...

Python酷库之旅-第三方库Pandas(139)
目录 一、用法精讲 626、pandas.plotting.scatter_matrix方法 626-1、语法 626-2、参数 626-3、功能 626-4、返回值 626-5、说明 626-6、用法 626-6-1、数据准备 626-6-2、代码示例 626-6-3、结果输出 627、pandas.plotting.table方法 627-1、语法 627-2、参数 …...

昇思学习打卡营学习记录:CycleGAN壁画修复
按照提示,运行实训代码 进入实训平台:https://xihe.mindspore.cn/projects 选择“jupyter 在线编辑器” 启动“Ascend开发环境” :Ascend开发环境需要申请,大家可以申请试试看 启动开发环境后,在左边的文件夹中&am…...

南京大学《软件分析》李越, 谭添——1. 导论
导论 主要概念: soundcompletePL领域概述 动手学习 本节无 文章目录 导论1. PL(Programming Language) 程序设计语言1.1 程序设计语言的三大研究方向1.2 与静态分析相关方向的介绍与对比静态程序分析动态软件测试形式化(formal)语义验证(verification) 2. 静态分析:2.1莱斯…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...
