DAY6 面向对象
概念
对象是一种特殊的数据结构，可以用来记住一个事物的数据，从而代表该事物，可以理解为一个模板表，总而言之万物皆对象，比如一个人、一个物体等。
怎么创建对象
先设计对象的模板，也就是对象的设计图：类。
例如：我们需要创建一个明星Star类，设计明星有哪些特征。
通过new关键字，每new一次类就得到一个新的对象。
对象执行原理
方法区：存储类文件
栈内存：方法的执行（先进后出）
堆内存：放在堆中
类的基本语法
构造器
无参构造器
构造器：是一种特殊方法，不能写返回值类型，名称必须是类名，构造器也可以重载
有参构造器
特点
创建对象时，对象会去调用构造器。
应用场景
创建对象时，同时完成对对象成员变量（属性）的初始化赋值。
注意事项
- 类默认就自带了一个无参构造器
- 如果为类定义了有参数构造器，类默认的无参数构造器就没有了，还想用无参数构造器，就必须自己手写一个无参数构造器出来。
THIS关键字
概念
this就是一个变量，可以用在方法中，来拿到当前对象，哪个对象调用这个方法，this就拿到哪个对象。
应用场景
this主要用来解决：变量名称冲突问题的。
封装
要求
类就是一种封装，但是要合理的隐藏，合理的暴露（比如汽车：就隐藏电路等内容，暴露轮胎等）
操作
如何合理隐藏：使用private关键字修饰成员变量，就只能在本类中被直接访问，其他任何地方不能直接访问。
如何合理暴露：使用public修饰（公开）的get和set方法合理暴露成员变量的取值和赋值。
JAVABEAN
概念
是一种特殊类，也叫实体类，类中要满足如下需求：
- 类中的成员变量全部私有，并提供public修饰的getter/setter方法
- 类中需要提供一个无参数构造器，有参数构造器可选
应用场景
STATIC关键字
修饰成员变量
类名.静态变量（推荐）,对象.静态变量（不推荐）
对象.实例变量
修饰成员方法
如果这个方法只是为了做一个功能且不需要直接访问对象的数据，那么就定义为静态方法；
如果这个方法是对象的行为，需要访问对象的数据，这个方法必须定义成实例方法；
应用场景
做工具类，比如验证码：(VerifyCodeUtil)工具类中的方法都是一些静态方法，每个方法用来完成一个功能，以便供给开发人员直接使用，可以提高了代码复用；调用方便，提高开发效率。
注意事项
静态方法中可以直接访问静态成员，不可以直接访问实例成员。
实例方法中既可以直接访问静态成员，也可以直接访问实例成员。
实例方法中可以出现this关键字，静态方法中不可以出现this关键字的。
相关文章：
DAY6 面向对象
概念 对象是一种特殊的数据结构，可以用来记住一个事物的数据，从而代表该事物，可以理解为一个模板表，总而言之万物皆对象，比如一个人、一个物体等。 怎么创建对象 先设计对象的模板，也就是对象的设计图&a…...
代码随想录 （三）—— 哈希表部分刷题
当我们想使用哈希法来解决问题的时候，我们一般会选择如下三种数据结构。 数组set （集合）map(映射) 在java中有就是，hashmap, LinkedHashMap, TreeMap ，HashTable 等 总结一下，当我们遇到了要快速判断一个…...
搜维尔科技：使用 SenseGlove Nova 2 远程操作机械手，实现了对鸡蛋的精细操控
使用SenseGlove Nova 2远程操作机械手，实现了对鸡蛋的精细操控 搜维尔科技：使用 SenseGlove Nova 2远程操作机械手，实现了对鸡蛋的精细操控...
Mybatis是什么？优缺点分别有哪些？
MyBatis 是一个开源的持久层框架，它提供了将 SQL 语句和 Java 对象进行映射的功能，使得开发者可以通过简单的配置来实现数据库操作，减少了手写 SQL 的工作量。 MyBatis 的优点： 1. 简单易用：MyBatis 采用了简单的配置…...
opencascade鼠标拖拽框选功能
1.首先在OccView中添加用于显示矩形框的类 //! rubber rectangle for the mouse selection.Handle(AIS_RubberBand) mRectBand; 2.设置框选的属性 mRectBand new AIS_RubberBand(); //设置属性 mRectBand->SetLineType(Aspect_TOL_SOLID); //设置变宽线型为实线 mRe…...
docker 部署 postgres
这里以postgres:12.6为例： 1. 拉取postgres镜像 docker pull postgres:12.62. 创建挂载目录 mkdir -p /mydata/docker/postgres-1/data3. 启动postgres容器 docker run --name postgres-12.6 \-e POSTGRES_PASSWORD123456 \-p 5432:5432 \-v /mydata/docker/pos…...
【重学 MySQL】五十、添加数据
【重学 MySQL】五十、添加数据 使用INSERT INTO语句添加数据基本语法示例插入多行数据注意事项 使用LOAD DATA INFILE语句批量添加数据其他插入数据的方式注意事项 在MySQL中，添加数据是数据库操作中的基本操作之一。 使用INSERT INTO语句添加数据 使用 INSERT IN…...
硬货！Zabbix监控AIX系统服务案例
本文将介绍如何使用Zabbix自定义键值脚本方式监控AIX 系统IBM CICS中间件进程服务以及日志文件等信息。 Customer Information Control System (CICS) Transaction Server 是 IBM 针对 z/OS 的多用途事务处理软件。这是一个功能强大的应用程序服务器，用于大型和小型…...
python常见面试题
1、什么是Python？为什么它会如此流行？ Python是一种解释的、高级的、通用的编程语言。 Python的设计理念是通过使用必要的空格与空行，增强代码的可读性。 它之所以受欢迎，就是因为它具有简单易用的语法。 ▍2、为什么Python执…...
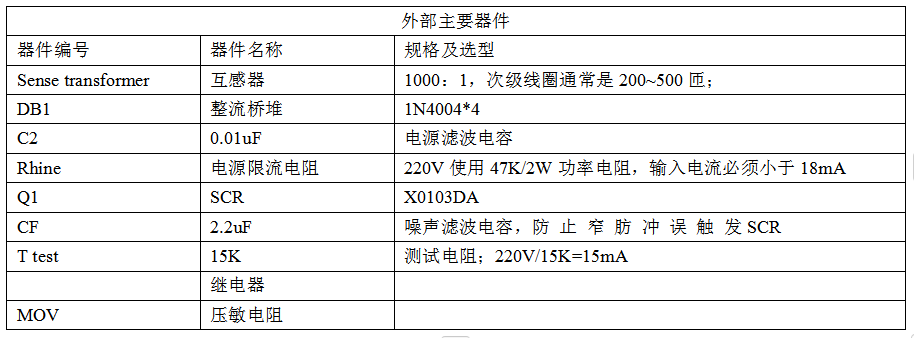
低功耗接地故障控制器D4145
一、概述 D4145 是一个接地故障断路器。它能够检测到不良的接地条件，譬如装置接触到水时，它会在有害或致命的电击发生之前将电路断开。 D4145能检测并保护从火线到地线,从零线到地线的故障.这种简单而传统的电路设计能够确保其应用自如和长时间的可靠性。…...
SpringMVC的处理流程
深入理解 SpringMVC 的请求处理流程：从用户请求到视图渲染的八个步骤 SpringMVC 是当前流行的基于 Java 的 Web 框架之一，它通过前端控制器 DispatcherServlet 将用户的 HTTP 请求统一接收并处理，随后将请求分发到具体的处理器（通…...
SpringBoot统一日志框架
在项目开发中，日志十分的重要，不管是记录运行情况还是定位线上问题，都离不开对日志的分析。 1.日志框架的选择 市面上常见的日志框架有很多，它们可以被分为两类：日志门面（日志抽象层）和日志实…...
vue-live2d看板娘集成方案设计使用教程
文章目录 前言v1.1.x版本：vue集成看板娘（暂不使用，在v1.2.x已替换）集成看板娘实现看板娘拖拽效果方案资源备份存储 当前最新调研：2024.10.2开源方案1：OhMyLive2D（推荐）开源方案2&…...
springboot接口如何支持400并发量
Spring Boot 本身并不直接限制并发量，但是你可以通过配置来优化应用以处理更多的并发请求。以下是一些关键配置和优化技巧： 服务器连接配置（application.properties 或 application.yml）: # 服务器连接数配置 server.tomcat.max…...
Verilog中的： `+:` 和 `-:`
: 和 -: 标准解释 logic [15:0] down_vect; logic [0:15] up_vect;down_vect[lsb_base_expr : width_expr] up_vect [msb_base_expr : width_expr] down_vect[msb_base_expr -: width_expr] up_vect [lsb_base_expr -: width_expr]举例 reg [31:0] dword; reg [7:0] byte0…...
为何四次挥手要等待2MSL
参考文章：https://zhuanlan.zhihu.com/p/204988465 A主动关闭连接一方，B是被动关闭一方 我们假设A发送了ACK报文后过了一段时间t之后B才收到该ACK，则有 0 < t < MSL。因为A并不知道它发送出去的ACK要多久对方才能收到，所以…...
C++——模拟实现list
1.初步实现结点和链表 namespace jxy {template<class T>struct list_node{T _data;list_node<T>* _prev;list_node<T>* _next;list_node(const T& x T()):_data(x),_prev(nullptr),_next(nullptr){}};template<class T>class list//list的框架本…...
React中useState、useReducer与useRef
useState 详解 useState 是 React 函数组件中用于管理组件状态的 Hook。它提供了一种简洁的方式来在函数组件中添加状态，并在状态改变时触发组件重新渲染。以下是 useState 的详细解析： 一、基本概念 useState 是一个函数，它接收一个初始状…...
ReGCL Rethinking Message Passingin Graph Contrastive Learning
AAAI24 推荐指数： #paper/⭐ 总体说：利用梯度对对比正负样本加权的。个人觉得和与正负样本加权没有区别，读完之后不想做笔记了。...
ubutun安装ffmpeg
安装依赖 sudo apt-get install yasm sudo apt-get install libsdl1.2-dev sudo apt-get install libsdl2-dev 下载安装 tar -zxvf filename.gz ./configure --enable-shared --prefix/usr/local/ffmpeg make -j4 sudo make install 添加路径 路径/usr/local/ffmpeg…...
【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现，玩家控制一个角色（龙）躲避障碍物（仙人掌和乌鸦）。以下是代码的详细介绍：…...
【JavaEE】-- HTTP
1. HTTP是什么？ HTTP（全称为"超文本传输协议"）是一种应用非常广泛的应用层协议，HTTP是基于TCP协议的一种应用层协议。 应用层协议：是计算机网络协议栈中最高层的协议，它定义了运行在不同主机上…...
2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...
Device Mapper 机制
Device Mapper 机制详解 Device Mapper（简称 DM）是 Linux 内核中的一套通用块设备映射框架，为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程，并配以详细的…...
管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...
【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变（硬件篇）
本项目是基于 STM32F103C8T6 微控制器的 SPWM（正弦脉宽调制）电源模块，能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路，图中 D1 为二极管， 其目的是防止正负极电源反接， …...
深入浅出深度学习基础：从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么？1.1.2 感知机的工作原理 1.2 感知机的简单应用：基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...
JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型（Primitive） 和 对象类型（Object） 两大类，共 8 种（ES11）： 一、原始类型（7种） 1. undefined 定…...
tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号，此时，我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...
Kubernetes 网络模型深度解析：Pod IP 与 Service 的负载均衡机制，Service到底是什么？
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址：Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址（如 10.244.1.2）无特殊名称：在 Kubernetes 中，它通常被称为 “Pod IP” 或 “容器 IP”生命周期：与 Pod …...