3.29 最小生成树算法
最小生成树概念
参考:什么是最小生成树?
Minimum Spanning Tree
何为生成树?
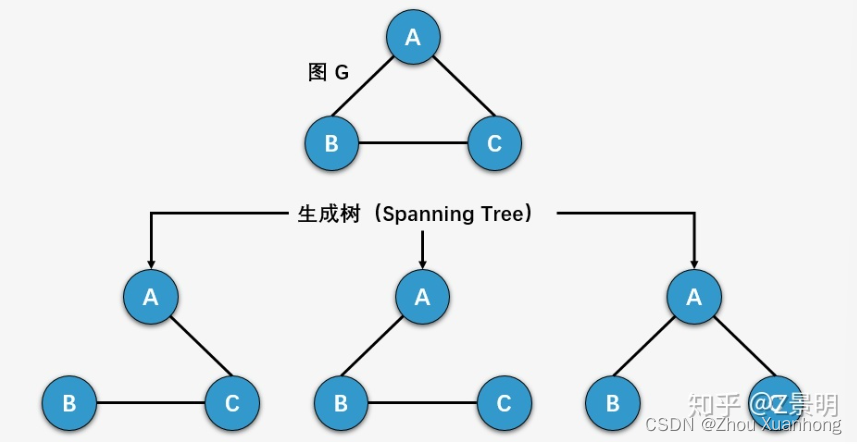
生成树是指一个联通图的极小的连通子图,它包含了图中的所有n个顶点,并只有n-1条边(构成一棵树)
生成树的一些性质:
- 一个连通图可以有多种生成树(如上图所示)
- 生成树中不存在环
- 任何一个边的加入都会使得生成树中出现环
何为最小生成树?
最小生成树是针对一个带权图来说的,就是指原图中能构成的所有生成树中,边权和最小的一颗生成树
对于下面的连通图:
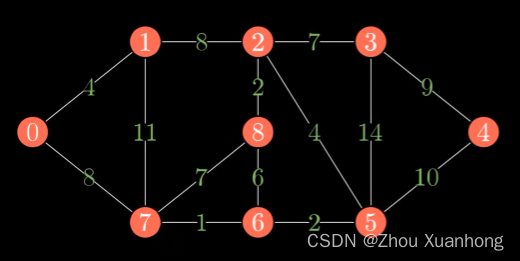
可以有多种选取边(即构成了生成树的情况):
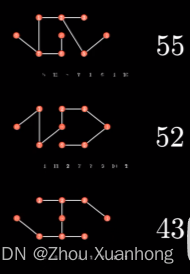
我们称权值和最小的树为最小生成树
最小生成树有什么意义呢?
接上图,如果我们需要在某城市之间修建道路,点与点之间的加权边就是两城市道路的维修费,如果我们想找到一种将所有城市都连通起来并且使得道路修建费用最小的一种方案,那么就要选择使用最小生成树。
最小生成树构建方法
两种方法都是基于贪心
有一点,其实我不太明白。“Kruskal算法维护的是边,所以不需要对于无向图存储两次边。Prim维护的是集合之间点的关系,因此需要对无向图存储两次边
克鲁斯卡尔算法(Kruskal)
算法思想
将所有的带权边按照权值从小到大排列,从最小的开始选择,如果加入该边后不会产生环,则加入,反之则不加入。直到已经选择了n-1条边。
这里不会产生环的判定比较困难,因此可以换一下想法:
就是只要选择的边的两端点不在同一连通块中即可。如下所示
使用并查集就可以检查联通问题了
#include<iostream>
#include<algorithm>using namespace std;const int N=2*1e5+10;int n,m;
int p[N];
int ans=0;//最终权值
int res=0;//已经放入的边数struct nn{int a;int b;int w;
}node[N];int cmp(nn a, nn b){return a.w<b.w;
}int find(int x){if(p[x]!=x) p[x]=find(p[x]);return p[x];
}int kruskal(){for(int i=1;i<=n;i++)p[i]=i;for(int i=1;i<=m;i++){//遍历m条边int a=node[i].a, b=node[i].b, w=node[i].w;a=find(a); b=find(b);if(a!=b){//如果不在一个联通图中p[a]=b;//连接两个点ans+=w;res++;}if(res==n-1){return res;}}return res;
}int main(){cin>>n>>m;for(int i=1;i<=m;i++){cin>>node[i].a>>node[i].b>>node[i].w;}sort(node+1,node+1+m,cmp);if(kruskal()==n-1)cout<<ans<<endl;elsecout<<"impossible"<<endl;return 0;
}
普里姆算法(Prim)
和kruskal算法(遍历边)不同的是,prim算法是对点进行遍历
算法思路
对于每个点,每次找到一个集合外的,距离该集合最近的点t。(该集合是一个已经确定了的连通块)
用点t更新集合外点到集合的距离,就是找集合外和t有连接的点,如果更小就更新,最后将点t放入集合中。(这里描述的不是很清楚)
st[j]==0&&(t==-1||dist[t]>dist[j]) 注意这里的判断,首先判断该点是否已经进入集合,然后再与上(t==-1和大小的或运算)
#include<iostream>
#include<algorithm>
#include<cstring>using namespace std;const int N=510,INF=0x3f3f3f3f;
int n,m;int g[N][N];//用于存储边
int dist[N];//点距离集合的距离
int st[N];//表示是否已经进入集合
int ans=0;int prim(){dist[1]=0;//强制一开始选择的点就是点1for(int i=1;i<=n;i++){//外层循环是指循环n次以遍历所有n个点int t=-1;for(int j=1;j<=n;j++){if(st[j]==0&&(t==-1||dist[t]>dist[j])){t=j;} }//找到最短的dist,下标为tif(dist[t]==INF) return INF;//说明没有点能够到达当前的集合ans+=dist[t];for(int j=1;j<=n;j++){if(st[j]==0&&j!=t){//更新所有集合外的点到该集合的距离dist[j]=min(dist[j],g[t][j]);}}st[t]=1;//将点加入集合}}int main(){cin>>n>>m;memset(g,0x3f,sizeof g);for(int i=1;i<=m;i++){int a,b,c;cin>>a>>b>>c;g[a][b]=g[b][a]=min(g[a][b],c);}memset(dist,0x3f,sizeof dist);if(prim()==INF)cout<<"impossible"<<endl;elsecout<<ans<<endl;return 0;
}
相关文章:

3.29 最小生成树算法
最小生成树概念 参考:什么是最小生成树? Minimum Spanning Tree 何为生成树? 生成树是指一个联通图的极小的连通子图,它包含了图中的所有n个顶点,并只有n-1条边(构成一棵树) 生成树的一些性…...

计算机科班与培训开发编程的区别在哪里?
科班、培训班、科班培训班的模式都培养了很多编程技术人员进入IT行业,有的成为某个技术领域的专家,有的成为领导层,有的一直在默默无闻的敲代码等待35岁的到来。不管那种方式入行,这些类似的情况都存在,并且未来还会一…...

idea设置常用自设置快捷键及坐标
<!--mybatis 依赖--> <dependency> <groupId>org.mybatis</groupId> <artifactId>mybatis</artifactId> <version>3.5.5</version> </dependency…...

Vue 3.0 实例方法
#$watch 参数:{string | Function} source{Function | Object} callback{Object} [options] {boolean} deep{boolean} immediate{string} flush返回:{Function} unwatch用法: 侦听组件实例上的响应式 property 或函数计算结果的变化。回调函数…...

日撸 Java 三百行day1-10
文章目录说明day1 环境搭建1.1 开发环境1.2 package import 和 println1.3 编写HelloWorld.javaday2 基本算术操作2.1 加、减、乘、除、整除、取余.day3 基本if 语句3.1 if条件分支语句3.2 代码day4 闰年的计算4.1 思路整理:何为闰年?4.2 核心代码day5 基…...
Ubuntu Instant-ngp 训练自有数据集
1. 运行环境配置 conda create -n instant-ngp python3.10 conda activate instant-ngp pip install -r requirements.txt -i https://pypi.tuna.tsinghua.edu.cn/simple2. COLMAP稀疏重建生成transform.json colmap 环境配置参考文档; 终端定位在instant-ngp/da…...

k8s集群只一台节点,重启节点后命名空间找不到了
定位 如果您的Kubernetes集群只有一台节点,并且在重启节点之前您创建了一些命名空间和资源,那么在节点重启后,这些命名空间和资源可能会丢失。这是因为在Kubernetes中,资源和命名空间通常是存储在etcd中的。当节点重启时…...
MarkDown示例
这里写自定义目录标题欢迎使用Markdown编辑器新的改变功能快捷键合理的创建标题,有助于目录的生成如何改变文本的样式插入链接与图片如何插入一段漂亮的代码片生成一个适合你的列表创建一个表格设定内容居中、居左、居右SmartyPants创建一个自定义列表如何创建一个注…...

spring cloud 雪崩效应
什么是雪崩效应 雪崩就是塌方。在山坡上的积雪,如果积雪的内聚力小于重力或其他力量,则积雪便向下滑动,从而逐渐引起积雪的崩塌。 在微服务架构中,服务之间通常存在级联调用。比如,服务A调用服务B,而服…...

Python 自动化指南(繁琐工作自动化)第二版:三、函数
原文:https://automatetheboringstuff.com/2e/chapter3/ 您已经熟悉了前几章中的print()、input()和len()函数。Python 提供了几个这样的内置函数,但是您也可以编写自己的函数。函数就像一个程序中的一个小程序。 为了更好地理解函数是如何工作的&#…...

c++多线程 1
https://www.runoob.com/cplusplus/cpp-multithreading.html 两种类型的多任务处理:基于进程和基于线程。 基于进程的多任务处理是程序的并发执行。 基于线程的多任务处理是同一程序的片段的并发执行。 线程 c11以后有了 标准库 1 函数 2 类成员函数 3 lambda函…...
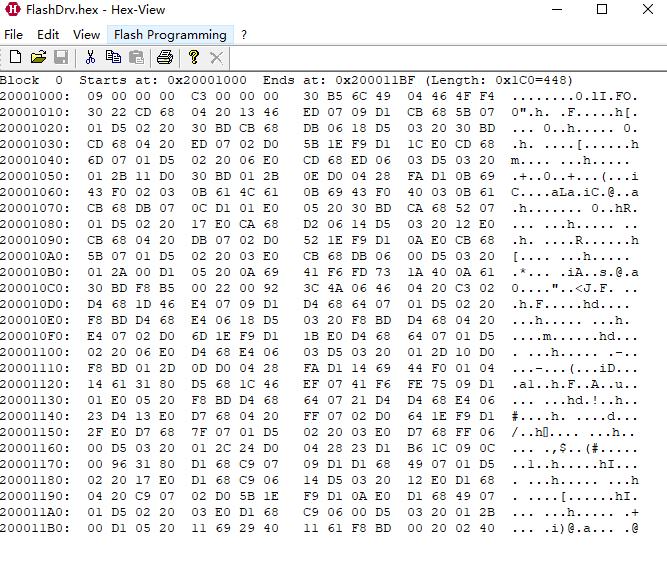
STM32F103制作FlashDriver
文章目录前言芯片内存定义实现过程FlashDriver生成段定义擦除函数写入函数编译后的map手动测试HexView提取指定地址内容并重映射总结前言 在汽车行业控制器软件刷新流程中,一般会将Flash驱动单独进行刷写,目的是防止程序中一直存在Flash驱动的话&#x…...
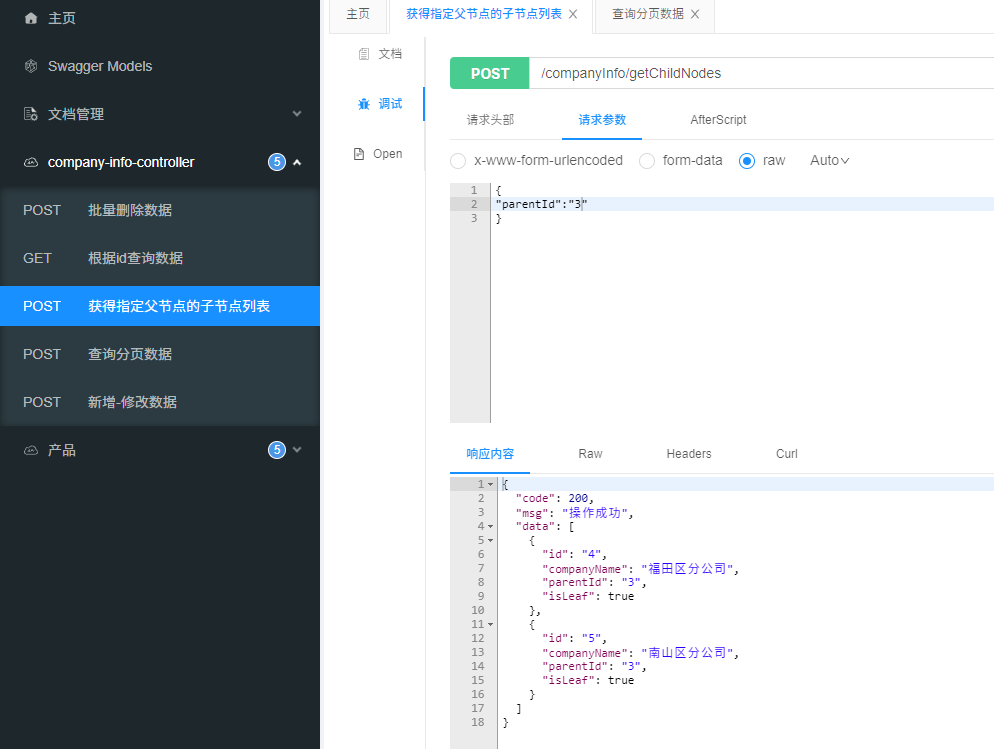
springboot树形结构接口, 懒加载实现
数据库关系有父子id的, 作为菜单栏展示时需要用前端需要用到懒加载, 所谓懒加载就是接口有一个标志位isLeaf, 前端请求后通过该字段判断该节点是否还有子节点数据 创建数据库表 t_company_info结构有id和parentId标识, 用来表示父子关系 /*Navicat Premium Data TransferSourc…...
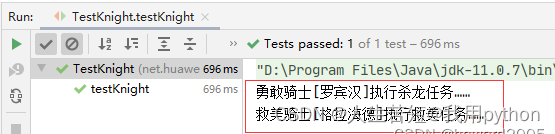
java企业级信息系统开发学习笔记02初探spring——利用组件注解符精简spring配置文件
文章目录一、学习目标二、打开01的项目三、利用组件注解符精简spring配置文件(一)创建新包,复制四个类(二)修改杀龙任务类(三)修改救美任务类(四)修改勇敢骑士类…...

用Python发送电子邮件?这也太丝滑了吧(21)
小朋友们好,大朋友们好! 我是猫妹,一名爱上Python编程的小学生。 欢迎和猫妹一起,趣味学Python。 今日主题 猫爸赚钱养家,细想起来真的不容易啊! 起早贪黑,都是6点早起做早饭,送…...

分类预测 | MATLAB实现CNN-GRU-Attention多输入分类预测
分类预测 | MATLAB实现CNN-GRU-Attention多输入分类预测 目录分类预测 | MATLAB实现CNN-GRU-Attention多输入分类预测分类效果模型描述程序设计参考资料分类效果 模型描述 Matlab实现CNN-GRU-Attention多变量分类预测 1.data为数据集,格式为excel,12个输…...

C++提高编程(1)
C提高编程1.模板1.1模板的概念1.2函数模板1.2.1函数模板语法1.2.2函数模板注意事项1.2.3函数模板案例1.2.4普通函数与函数模板的区别1.2.5普通函数与函数模板的调用规则1.2.6模板的局限性1.3类模板1.3.1类模板语法1.3.2类模板和函数模板区别1.3.3类模板中成员函数创建时机1.3.4…...

day26 回溯算法的部分总结
回溯算法的部分总结 回溯算法是一种常用于解决排列组合问题、搜索问题的算法,它的基本思想是将问题的解空间转化为一棵树,通过深度优先搜索的方式遍历树上的所有节点,找到符合条件的解。回溯算法通常使用递归实现,每次递归时传入…...

带你玩转Python爬虫(胆小者勿进)千万别做坏事·······
这节课很危险,哈哈哈哈,逗你们玩的 目录 写在前面 1 了解robots.txt 1.1 基础理解 1.2 使用robots.txt 2 Cookie 2.1 两种cookie处理方式 3 常用爬虫方法 3.1 bs4 3.1.1 基础介绍 3.1.2 bs4使用 3.1.2 使用例子 3.2 xpath 3.2.1 xpath基础介…...
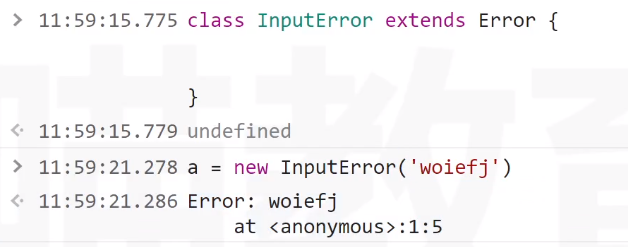
【JavaScript 】严格模式,With关键字,测试框架介绍,assert
❤️ Author: 老九 ☕️ 个人博客:老九的CSDN博客 🙏 个人名言:不可控之事 乐观面对 😍 系列专栏: 文章目录静态类型语言弱类型严格模式将过失错误转化为异常简化变量的使用With测试框架try-catch选择性捕获…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...

麒麟系统使用-进行.NET开发
文章目录 前言一、搭建dotnet环境1.获取相关资源2.配置dotnet 二、使用dotnet三、其他说明总结 前言 麒麟系统的内核是基于linux的,如果需要进行.NET开发,则需要安装特定的应用。由于NET Framework 是仅适用于 Windows 版本的 .NET,所以要进…...

Cursor AI 账号纯净度维护与高效注册指南
Cursor AI 账号纯净度维护与高效注册指南:解决限制问题的实战方案 风车无限免费邮箱系统网页端使用说明|快速获取邮箱|cursor|windsurf|augment 问题背景 在成功解决 Cursor 环境配置问题后,许多开发者仍面临账号纯净度不足导致的限制问题。无论使用 16…...