【数据结构】用Java实现一棵二叉树
目录
前言
1. 创建MyBinaryTree类
2. 从前序与中序遍历序列构造二叉树
3. 从中序与后序遍历序列构造二叉树
4. 用层序遍历验证二叉树是否构建成功
5. 整体代码(构建二叉树、二叉树的基本功能和测试代码)
6. 测试结果
前言
前面两篇文章已经给出了如何构建二叉树以及如何实现基本功能,感兴趣的友友可以点下面的链接看一看,在这里给出构建二叉树的简单说明以及构建二叉树和实现基本功能实现的代码。
二叉树的构建
二叉树的基本操作
// 前序遍历void preOrder(TreeNode root); // 中序遍历void inOrder(TreeNode root);// 后序遍历void postOrder(TreeNode root);// 获取树中节点的个数:遍历思路public static int nodeSize;void size(TreeNode root);// 获取节点的个数:子问题的思路int size2(TreeNode root);//获取叶子节点的个数:遍历思路public static int leafSize = 0;void getLeafNodeCount1(TreeNode root);// 获取叶子节点的个数:子问题int getLeafNodeCount2(TreeNode root);// 获取第K层节点的个数int getKLevelNodeCount(TreeNode root, int k);// 获取二叉树的高度,时间复杂度:O(N)int getHeight(TreeNode root);// 检测值为value的元素是否存在TreeNode find(TreeNode root, char val);//层序遍历void levelOrder(TreeNode root);// 判断一棵树是不是完全二叉树boolean isCompleteTree(TreeNode root);1. 创建MyBinaryTree类
val存储二叉树节点的值,left为二叉树的左子树,right为二叉树右子树地址。
下面的所有方法都是在MyBinaryTree类中实现的。
public class MyBinaryTree {static class TreeNode {public int val;TreeNode left;//左孩子的引用TreeNode right;//右孩子的引用public TreeNode(int val) {this.val = val;}}}2. 从前序与中序遍历序列构造二叉树
从前序遍历中获取根节点,中序遍历中根节点前面的是左子树的部分,中序遍历中根节点后面的是右子树部分。使用index下标来遍历前序数组。
1. 从前序遍历结果中获取到树的根节点
2. 在中序遍历结果中确定根节点的位置,按照该位置将中序遍历结果分为两部分
左半部分是根节点的左子树,递归创建根节点的左子树
右半部分是根节点的右子树,递归创建根节点的右子树
public TreeNode buildTree1(int[] preorder, int[] inorder) {return buildTreeHelper1(preorder,inorder,0,inorder.length - 1);}int index = 0;private TreeNode buildTreeHelper1(int[] preorder, int[] inorder, int left, int right) {if(index == inorder.length ){return null;}if (left > right){return null;}int pos = find(inorder,preorder);TreeNode root = new TreeNode(preorder[index]);index ++;root.left = buildTreeHelper1(preorder,inorder,left,pos - 1);root.right = buildTreeHelper1(preorder,inorder,pos + 1,right);return root;}private int find(int[] inorder,int[] preorder) {for (int i = 0; i < inorder.length; i++) {if (inorder[i] == preorder[index]){return i;}}return -1;}3. 从中序与后序遍历序列构造二叉树
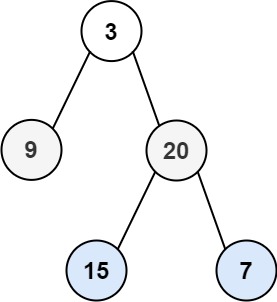
先看看同一颗树的前序遍历结果preorder = [3,9,20,15,7]和后序遍历的结果postorder = [9,15,7,20,3],对比一下这两。
发现将后序遍历的结果反转->[3,20,7,15,9],前序遍历是根左右,后序遍历反转后的是根右左,所以我们只需要将后序遍历的结果反转一下,然后向上一题那样构建二叉树,只不过是先构建右子树再构建左子树。
// 从中序与后序遍历序列构造二叉树, 返回这棵树的根节点public TreeNode buildTree2(int[] postorder, int[] inorder) {reverse(postorder);return buildTreeHelper2(postorder,inorder,0,inorder.length - 1);}private void reverse(int[] postorder){for (int i = 0; i < postorder.length/2; i++) {int temp = postorder[i];postorder[i] = postorder[postorder.length - i - 1];postorder[postorder.length - i - 1] = temp;}}private TreeNode buildTreeHelper2(int[] postorder, int[] inorder, int left, int right) {if(index == inorder.length ){return null;}if (left > right){return null;}int pos = find(inorder,postorder);TreeNode root = new TreeNode(postorder[index]);index ++;root.right = buildTreeHelper2(postorder,inorder,pos + 1,right);root.left = buildTreeHelper2(postorder,inorder,left,pos - 1);return root;}4. 用层序遍历验证二叉树是否构建成功
1. 如果是空树直接返回
2. 层序遍历需要用到队列,定义一个队列,里面放置节点的地址,将根节点如队列
3. 队列非空时,循环进行一下操作:
a. 队列中当前元素都是在同一层的,依次取出遍历,保存到同一个curList中
取到一个节点时候,
>> 保存该节点
>> 如果该节点左子树存在,将该左子树入队列
>> 如果该节点右子树存在,将该节点右子树入队列
>> 将当前已遍历节点从队列中拿出来
b. 本层节点遍历结束后,保存到返回的curList中,此时下一层节点已经全部入队列
public void levelOrder(TreeNode root) {List<List<Integer>> list = new ArrayList<>();if (root == null){System.out.println(list);return;}Deque<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()){int size = queue.size();List<Integer> curList = new ArrayList<>();for (int i = 0; i < size; i++) {TreeNode temp = queue.pop();curList.add(temp.val);if (temp.left != null){queue.offer(temp.left);}if (temp.right != null){queue.offer(temp.right);}}list.add(curList);}System.out.println(list);}5. 整体代码(构建二叉树、二叉树的基本功能和测试代码)
构建的二叉树:
import java.util.ArrayList;
import java.util.Deque;
import java.util.LinkedList;
import java.util.List;public class MyBinaryTree {static class TreeNode {public int val;TreeNode left;//左孩子的引用TreeNode right;//右孩子的引用public TreeNode(int val) {this.val = val;}}// 从前序与中序遍历序列构造二叉树, 返回这棵树的根节点public TreeNode buildTree1(int[] preorder, int[] inorder) {return buildTreeHelper1(preorder,inorder,0,inorder.length - 1);}int index = 0;private TreeNode buildTreeHelper1(int[] preorder, int[] inorder, int left, int right) {if(index == inorder.length ){return null;}if (left > right){return null;}int pos = find(inorder,preorder);TreeNode root = new TreeNode(preorder[index]);index ++;root.left = buildTreeHelper1(preorder,inorder,left,pos - 1);root.right = buildTreeHelper1(preorder,inorder,pos + 1,right);return root;}private int find(int[] inorder,int[] preorder) {for (int i = 0; i < inorder.length; i++) {if (inorder[i] == preorder[index]){return i;}}return -1;}// 从中序与后序遍历序列构造二叉树, 返回这棵树的根节点public TreeNode buildTree2(int[] postorder, int[] inorder) {reverse(postorder);return buildTreeHelper2(postorder,inorder,0,inorder.length - 1);}private void reverse(int[] postorder){for (int i = 0; i < postorder.length/2; i++) {int temp = postorder[i];postorder[i] = postorder[postorder.length - i - 1];postorder[postorder.length - i - 1] = temp;}}private TreeNode buildTreeHelper2(int[] postorder, int[] inorder, int left, int right) {if(index == inorder.length ){return null;}if (left > right){return null;}int pos = find(inorder,postorder);TreeNode root = new TreeNode(postorder[index]);index ++;root.right = buildTreeHelper2(postorder,inorder,pos + 1,right);root.left = buildTreeHelper2(postorder,inorder,left,pos - 1);return root;}// 层序遍历
// 用数组输出层序遍历结果public void levelOrder(TreeNode root) {List<List<Integer>> list = new ArrayList<>();if (root == null){System.out.println(list);return;}Deque<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()){int size = queue.size();List<Integer> curList = new ArrayList<>();for (int i = 0; i < size; i++) {TreeNode temp = queue.pop();curList.add(temp.val);if (temp.left != null){queue.offer(temp.left);}if (temp.right != null){queue.offer(temp.right);}}list.add(curList);}System.out.println(list);}
// 直接输出结果
// void levelOrder(TreeNode root) {
// if (root == null){
// System.out.println("这是颗空树!!!");
// return;
// }
// Deque<TreeNode> queue = new LinkedList<>();
// queue.offer(root);
// while (!queue.isEmpty()){
// TreeNode cur = queue.pop();
// System.out.print(cur.val + " ");
// if (cur.left != null){
// queue.offer(cur.left);
// }
// if (cur.right != null){
// queue.offer(cur.right);
// }
// }
// }// 前序遍历public void preOrder(TreeNode root) {if(root == null){return;}System.out.print(root.val + " ");preOrder(root.left);preOrder(root.right);}// 中序遍历void inOrder(TreeNode root) {if(root == null){return;}inOrder(root.left);System.out.print(root.val + " ");inOrder(root.right);}// 后序遍历void postOrder(TreeNode root) {if(root == null){return;}postOrder(root.left);postOrder(root.right);System.out.print(root.val + " ");}public static int nodeSize;/*** 获取树中节点的个数:遍历思路*/void size(TreeNode root) {if (root == null){return;}nodeSize ++;size(root.left);size(root.right);}/*** 获取节点的个数:子问题的思路*/int size2(TreeNode root) {if (root == null) return 0;return size2(root.left) + size2(root.right) + 1;}/*获取叶子节点的个数:遍历思路*/public static int leafSize = 0;void getLeafNodeCount1(TreeNode root) {if(root == null){return;}if (root.left == null && root.right == null){leafSize ++;}getLeafNodeCount1(root.left);getLeafNodeCount1(root.right);}/*获取叶子节点的个数:子问题*/int getLeafNodeCount2(TreeNode root) {if (root == null) return 0;if (root.left == null && root.right == null) {return 1;}return getLeafNodeCount2(root.left) + getLeafNodeCount2(root.right);}/*获取第K层节点的个数*/int getKLevelNodeCount(TreeNode root, int k) {if (root == null || k <= 0){return 0;}if (k == 1){return 1;}return getKLevelNodeCount(root.left,k - 1) + getKLevelNodeCount(root.right,k - 1);}/*获取二叉树的高度时间复杂度:O(N)*/int getHeight(TreeNode root) {if (root == null){return 0;}if(root.left == null && root.right == null){return 1;}return 1 + Math.max(getHeight(root.left),getHeight(root.right));}// 检测值为value的元素是否存在TreeNode find(TreeNode root, char val) {if (root == null){return null;}if (root.val == val){return root;}TreeNode node = find(root.left,val);if (node != null){return node;}return find(root.right,val);}// 判断一棵树是不是完全二叉树boolean isCompleteTree(TreeNode root) {Deque<TreeNode> queue = new LinkedList<>();queue.offer(root);boolean isStep1 = true;while (!queue.isEmpty()){TreeNode node = queue.poll();if(isStep1){if(node.left != null && node.right != null){queue.offer(node.left);queue.offer(node.right);} else if (node.left != null) {queue.offer(node.left);isStep1 = false;} else if (node.right != null){return false;}else {isStep1 = false;}}else {if(node.left != null || node.right != null){return false;}}}return true;}public static void main(String[] args) {MyBinaryTree tree = new MyBinaryTree();//用前序遍历和后序遍历构建二叉树int[] pre = {3,9,20,15,7};int[] in = {9,3,15,20,7};TreeNode root = tree.buildTree1(pre,in);System.out.println("前序遍历");tree.preOrder(root);System.out.println();System.out.println("中序遍历");tree.inOrder(root);System.out.println();System.out.println("后序遍历");tree.postOrder(root);System.out.println();System.out.println("层序遍历");tree.levelOrder(root);System.out.println();System.out.println("统计树的节点个数");tree.size(root);System.out.println(nodeSize);System.out.println("统计叶子节点个数");tree.getLeafNodeCount1(root);System.out.println(leafSize);System.out.println("树的高度");System.out.println(tree.getHeight(root));System.out.println("检测树中值为val的元素是否存在 Q B");
// System.out.println(tree.find(root,'x').val);if (tree.find(root,'Q') == null){System.out.println("没有找到该元素");}else {System.out.println(tree.find(root,'x').val);}if (tree.find(root,'B') == null){System.out.println("没有找到该元素");}else {System.out.println(tree.find(root,'B').val);}System.out.println("获取第K层节点的个数");System.out.println(tree.getKLevelNodeCount(root,3));System.out.println("判断一棵树是不是完全二叉树");System.out.println(tree.isCompleteTree(root));}
}
6. 测试结果

相关文章:

【数据结构】用Java实现一棵二叉树
目录 前言 1. 创建MyBinaryTree类 2. 从前序与中序遍历序列构造二叉树 3. 从中序与后序遍历序列构造二叉树 4. 用层序遍历验证二叉树是否构建成功 5. 整体代码(构建二叉树、二叉树的基本功能和测试代码) 6. 测试结果 前言 前面两篇文章已经给出了…...
【面试】面试官问的几率较大的网络安全面试题
文章目录防范常见的 Web 攻击1、什么是SQL注入攻击2、什么是XSS攻击3、什么是CSRF攻击4、什么是文件上传漏洞5、DDos 攻击重要协议分布图1、arp协议的工作原理ARP协议工作原理:2、什么是RARP?工作原理3、dns是什么?dns的工作原理4、rip协议是…...

[Python] 循环语句
循环语句就是在符合条件的情况下,重复执行一个代码段 1.while循环 while语句可用于在条件为真时反复执行代码块 语法格式 while 条件语句:执行语句 当条件语句为真(True)时,就会执行while循环下的语句 示例 实现1到100 的累加并输出求和结果 …...
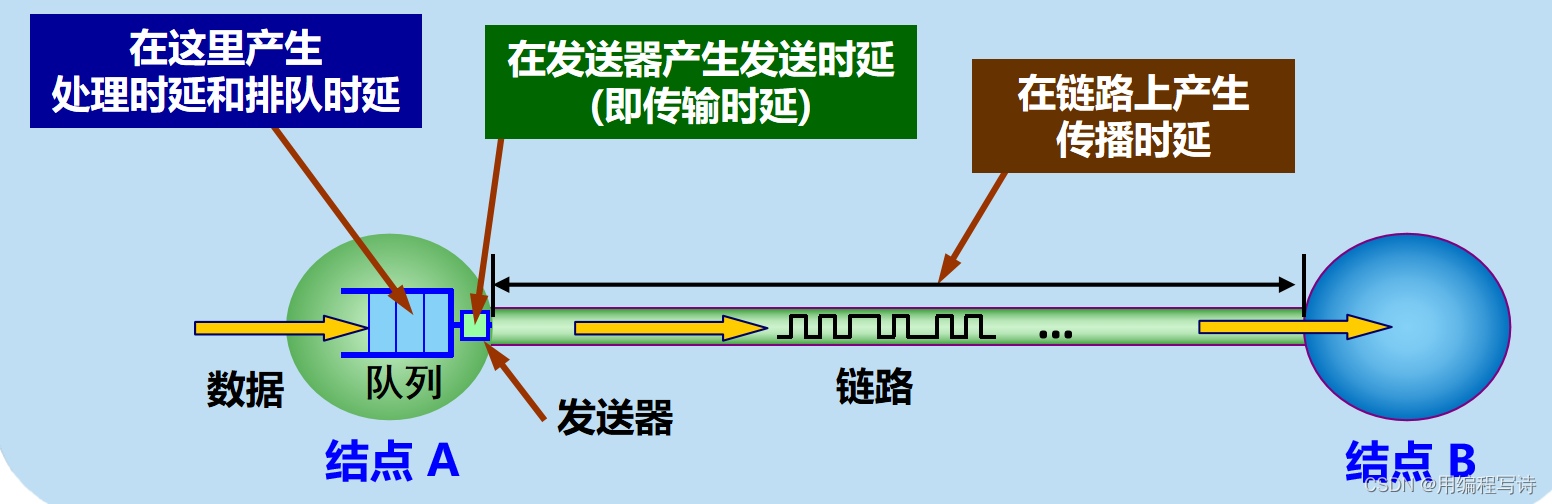
计算机网络考试复习——第一章 1.5 1.6
1.5 计算机网络的类别 1.5.1计算机网络的定义: 系统集合,连接起来,协议工作,资源共享 计算机网络主要是由一些通用的、可编程的硬件互连而成的,而这些硬件并非专门用来实现某一特定目的(例如࿰…...

3.29 最小生成树算法
最小生成树概念 参考:什么是最小生成树? Minimum Spanning Tree 何为生成树? 生成树是指一个联通图的极小的连通子图,它包含了图中的所有n个顶点,并只有n-1条边(构成一棵树) 生成树的一些性…...

计算机科班与培训开发编程的区别在哪里?
科班、培训班、科班培训班的模式都培养了很多编程技术人员进入IT行业,有的成为某个技术领域的专家,有的成为领导层,有的一直在默默无闻的敲代码等待35岁的到来。不管那种方式入行,这些类似的情况都存在,并且未来还会一…...

idea设置常用自设置快捷键及坐标
<!--mybatis 依赖--> <dependency> <groupId>org.mybatis</groupId> <artifactId>mybatis</artifactId> <version>3.5.5</version> </dependency…...

Vue 3.0 实例方法
#$watch 参数:{string | Function} source{Function | Object} callback{Object} [options] {boolean} deep{boolean} immediate{string} flush返回:{Function} unwatch用法: 侦听组件实例上的响应式 property 或函数计算结果的变化。回调函数…...

日撸 Java 三百行day1-10
文章目录说明day1 环境搭建1.1 开发环境1.2 package import 和 println1.3 编写HelloWorld.javaday2 基本算术操作2.1 加、减、乘、除、整除、取余.day3 基本if 语句3.1 if条件分支语句3.2 代码day4 闰年的计算4.1 思路整理:何为闰年?4.2 核心代码day5 基…...
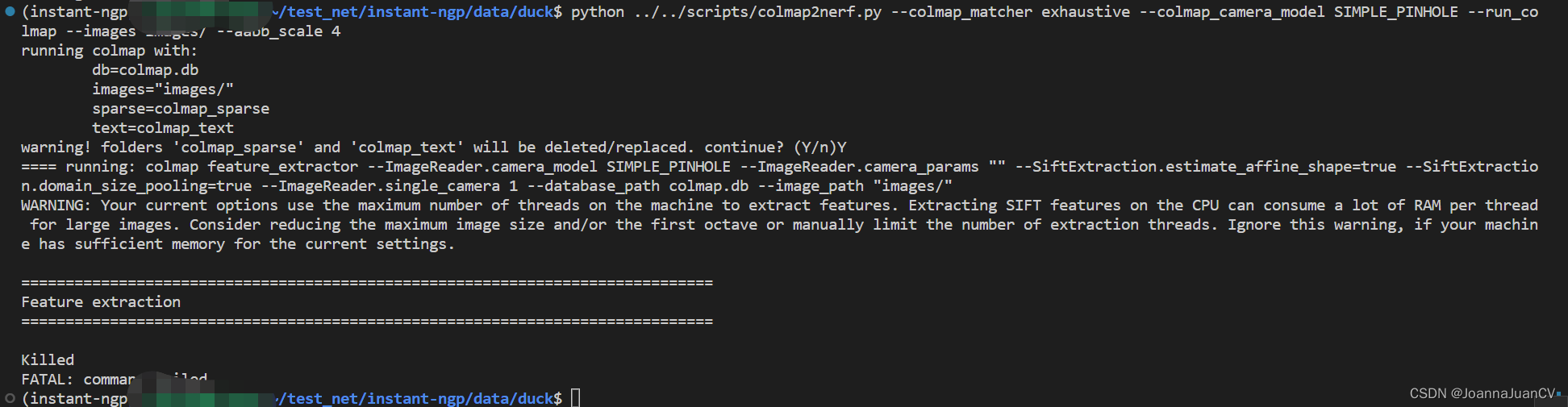
Ubuntu Instant-ngp 训练自有数据集
1. 运行环境配置 conda create -n instant-ngp python3.10 conda activate instant-ngp pip install -r requirements.txt -i https://pypi.tuna.tsinghua.edu.cn/simple2. COLMAP稀疏重建生成transform.json colmap 环境配置参考文档; 终端定位在instant-ngp/da…...

k8s集群只一台节点,重启节点后命名空间找不到了
定位 如果您的Kubernetes集群只有一台节点,并且在重启节点之前您创建了一些命名空间和资源,那么在节点重启后,这些命名空间和资源可能会丢失。这是因为在Kubernetes中,资源和命名空间通常是存储在etcd中的。当节点重启时…...
MarkDown示例
这里写自定义目录标题欢迎使用Markdown编辑器新的改变功能快捷键合理的创建标题,有助于目录的生成如何改变文本的样式插入链接与图片如何插入一段漂亮的代码片生成一个适合你的列表创建一个表格设定内容居中、居左、居右SmartyPants创建一个自定义列表如何创建一个注…...

spring cloud 雪崩效应
什么是雪崩效应 雪崩就是塌方。在山坡上的积雪,如果积雪的内聚力小于重力或其他力量,则积雪便向下滑动,从而逐渐引起积雪的崩塌。 在微服务架构中,服务之间通常存在级联调用。比如,服务A调用服务B,而服…...

Python 自动化指南(繁琐工作自动化)第二版:三、函数
原文:https://automatetheboringstuff.com/2e/chapter3/ 您已经熟悉了前几章中的print()、input()和len()函数。Python 提供了几个这样的内置函数,但是您也可以编写自己的函数。函数就像一个程序中的一个小程序。 为了更好地理解函数是如何工作的&#…...

c++多线程 1
https://www.runoob.com/cplusplus/cpp-multithreading.html 两种类型的多任务处理:基于进程和基于线程。 基于进程的多任务处理是程序的并发执行。 基于线程的多任务处理是同一程序的片段的并发执行。 线程 c11以后有了 标准库 1 函数 2 类成员函数 3 lambda函…...
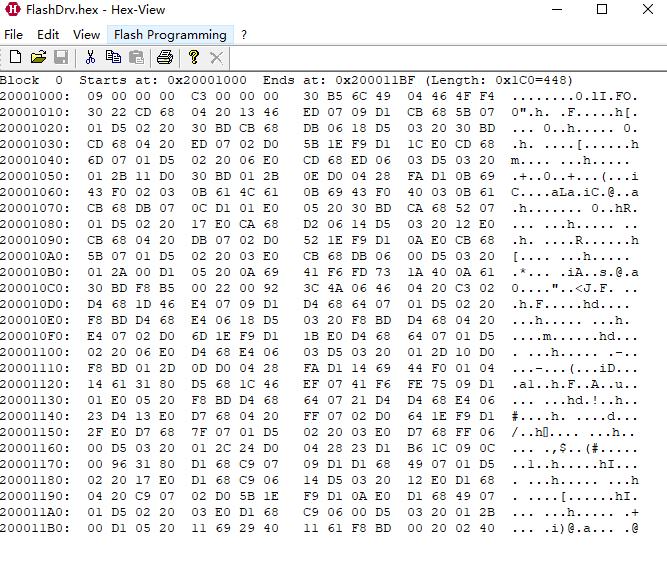
STM32F103制作FlashDriver
文章目录前言芯片内存定义实现过程FlashDriver生成段定义擦除函数写入函数编译后的map手动测试HexView提取指定地址内容并重映射总结前言 在汽车行业控制器软件刷新流程中,一般会将Flash驱动单独进行刷写,目的是防止程序中一直存在Flash驱动的话&#x…...
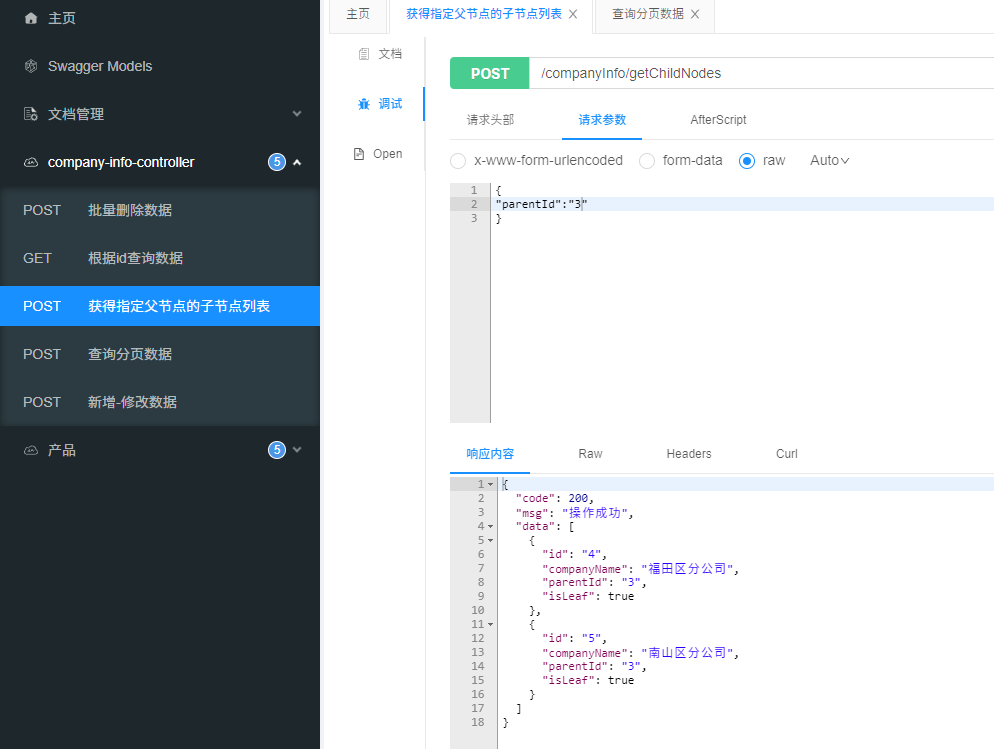
springboot树形结构接口, 懒加载实现
数据库关系有父子id的, 作为菜单栏展示时需要用前端需要用到懒加载, 所谓懒加载就是接口有一个标志位isLeaf, 前端请求后通过该字段判断该节点是否还有子节点数据 创建数据库表 t_company_info结构有id和parentId标识, 用来表示父子关系 /*Navicat Premium Data TransferSourc…...
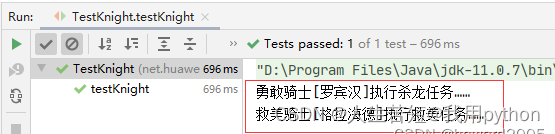
java企业级信息系统开发学习笔记02初探spring——利用组件注解符精简spring配置文件
文章目录一、学习目标二、打开01的项目三、利用组件注解符精简spring配置文件(一)创建新包,复制四个类(二)修改杀龙任务类(三)修改救美任务类(四)修改勇敢骑士类…...

用Python发送电子邮件?这也太丝滑了吧(21)
小朋友们好,大朋友们好! 我是猫妹,一名爱上Python编程的小学生。 欢迎和猫妹一起,趣味学Python。 今日主题 猫爸赚钱养家,细想起来真的不容易啊! 起早贪黑,都是6点早起做早饭,送…...

分类预测 | MATLAB实现CNN-GRU-Attention多输入分类预测
分类预测 | MATLAB实现CNN-GRU-Attention多输入分类预测 目录分类预测 | MATLAB实现CNN-GRU-Attention多输入分类预测分类效果模型描述程序设计参考资料分类效果 模型描述 Matlab实现CNN-GRU-Attention多变量分类预测 1.data为数据集,格式为excel,12个输…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

VSCode 使用CMake 构建 Qt 5 窗口程序
首先,目录结构如下图: 运行效果: cmake -B build cmake --build build 运行: windeployqt.exe F:\testQt5\build\Debug\app.exe main.cpp #include "mainwindow.h"#include <QAppli...

简单介绍C++中 string与wstring
在C中,string和wstring是两种用于处理不同字符编码的字符串类型,分别基于char和wchar_t字符类型。以下是它们的详细说明和对比: 1. 基础定义 string 类型:std::string 字符类型:char(通常为8位)…...
