推迟参数设计的自适应反步控制和自适应神经网络的反步控制设计
推迟参数设计的自适应反步控制和自适应神经网络的反步控制设计

目录
- 推迟参数设计的自适应反步控制和自适应神经网络的反步控制设计
- 前言
- 匹配与非匹配
- 1. 基于自适应反步控制的非匹配条件下的系统控制器设计
- 问题描述
- 控制器设计
- 小结
- 2. 基于自适应反步控制和推迟参数设计的非匹配条件下的系统控制器设计
- 问题描述
- 控制器设计
- 小结
- 3. 基于自适应神经网络+反步控制+推迟参数设计的非匹配条件下的系统控制器设计
- 问题描述
- 控制器设计
- 小结
- 总结
前言
在上一篇文章中,我们从反步法出发,分析基于反步法的跟踪控制设计,以及含有未知参数的自适应反步控制的控制器设计。
上一篇文章链接:Adaptive Backstepping Besign自适应反步控制设计_ADi_hhh的博客
但是上一篇文章中的系统满足匹配条件,比较容易设计。本篇文章针对不满足匹配条件的系统进行自适应反步设计,并针对系统中含有未知参数的系统进行自适应神经网络的的反步控制设计。
匹配与非匹配
在控制理论中的不确定性可以分为两类。当控制输入可以克服不确定性时,系统就是在匹配条件下的,或者看网上有人说不确定性是在控制矩阵B所张成的空间中;而当控制输入不在控制输入下时,系统就是在不匹配条件下的,不能通过控制量的设计来抵消其影响。
举例如下:
上一篇文章中:
x˙1=f1(x1)+x2x˙2=f2(x1,x2)θ+buy=x1\begin{aligned} \dot x_1&=f_1(x_1)+x_2\\ \dot x_2&=f_2(x_1,x_2)\theta+bu\\ y&=x_1 \end{aligned} x˙1x˙2y=f1(x1)+x2=f2(x1,x2)θ+bu=x1
这样的系统就是匹配条件下的系统,因而我们能通过自适应反步控制设计,设计出控制器和参数更新率。
而形如
x˙1=f1(x1)θ+x2x˙2=uy=x1(1)\begin{aligned} \dot x_1&=f_1(x_1)\theta+x_2\\ \dot x_2&=u\\ y&=x_1 \end{aligned} \qquad(1) x˙1x˙2y=f1(x1)θ+x2=u=x1(1)
则是非匹配的,控制输入无法直接抵消不确定量θ\thetaθ所带来的影响。需要利用反步设计、鲁棒控制等其他方法来设计控制器。
1. 基于自适应反步控制的非匹配条件下的系统控制器设计
问题描述
针对形如公式(1)的系统进行控制器设计,其中f1(x)f_1(x)f1(x)是已知的函数,θ\thetaθ为未知参数,设计控制器使得y→ydy→y_dy→yd,并且ydy_dyd的导数可知。
我们首先按照前面的自适应反步控制方法来设计控制器。
控制器设计
-
定义系统误差:z1=y−yd=x1−ydz_1=y-y_d=x_1-y_dz1=y−yd=x1−yd(为什么不用e来表示误差了?别问,问就是显得专业)
-
系统误差的动态方程:
z˙1=x˙1−y˙d=f1(x1)θ+x2−y˙d\begin{aligned} \dot z_1 &=\dot x_1 -\dot y_d\\ &=f_1(x_1) \theta+x_2-\dot y_d \end{aligned} z˙1=x˙1−y˙d=f1(x1)θ+x2−y˙d -
考虑如下候选李亚普诺夫函数:V1=12z12V_1 = \frac{1}{2}z_1^2V1=21z12
对其求导得:
V˙1=z1z˙1=z1(f1(x1)θ+x2−y˙d)\begin{aligned} \dot V_1 &=z_1\dot z_1\\ & = z_1(f_1(x_1)\theta+x_2-\dot y_d) \end{aligned} V˙1=z1z˙1=z1(f1(x1)θ+x2−y˙d)
这时候我们可以把x2x_2x2当作一个输入量,那么假如
x2=−k1z1−f1(x1)θ^+y˙dx_2=-k_1z_1-f_1(x_1) \hat\theta+\dot y_d x2=−k1z1−f1(x1)θ^+y˙d
其中θ^\hat \thetaθ^是对θ\thetaθ的估计,估计误差为θ~=θ^−θ\tilde \theta=\hat \theta-\thetaθ~=θ^−θ,引入一虚拟控制量α1\alpha_1α1,即令$\alpha_1=-k_1z_1-f_1(x_1) \hat\theta+\dot y_d $此时可以定义出第二个误差为z2=x2−α1z_2=x_2-\alpha_1z2=x2−α1
因为引入了新的估计误差θ~\tilde \thetaθ~,因此考虑如下候选李雅普诺夫函数:
V2=V1+12γθ~2V_2=V_1+\frac{1}{2 \gamma}\tilde \theta^2 V2=V1+2γ1θ~2
对其求导得:
V˙2=V˙1+1γθ~θ^˙=z1(f1(x1)θ+x2−y˙d)+1γθ~θ^˙=z1(f1(x1)θ+z2+α1−y˙d)+1γθ~θ^˙=z1(f1(x1)θ+z2+(−k1z1−f1(x1)θ^+y˙d)−y˙d)+1γθ~θ^˙=−k1z12+z1z2+θ~(−z1f1(x1)+1γθ^˙)(∗)\begin{aligned} \dot V_2&=\dot V_1+\frac{1}{\gamma}\tilde \theta \dot{\hat \theta}\\ &=z_1(f_1(x_1)\theta+x_2-\dot y_d)+\frac{1}{\gamma}\tilde \theta \dot{\hat \theta}\\ &=z_1(f_1(x_1)\theta+z_2+\alpha_1-\dot y_d)+\frac{1}{\gamma}\tilde \theta \dot{\hat \theta}\\ &=z_1(f_1(x_1)\theta+z_2+(-k_1z_1-f_1(x_1) \hat\theta+\dot y_d)-\dot y_d)+\frac{1}{\gamma}\tilde \theta \dot{\hat \theta}\\ &=-k_1z_1^2+z_1z_2+\tilde \theta(-z_1f_1(x_1)+\frac{1}{\gamma} \dot{\hat \theta}) \end{aligned}\qquad(*) V˙2=V˙1+γ1θ~θ^˙=z1(f1(x1)θ+x2−y˙d)+γ1θ~θ^˙=z1(f1(x1)θ+z2+α1−y˙d)+γ1θ~θ^˙=z1(f1(x1)θ+z2+(−k1z1−f1(x1)θ^+y˙d)−y˙d)+γ1θ~θ^˙=−k1z12+z1z2+θ~(−z1f1(x1)+γ1θ^˙)(∗)
则可以设计出参数更新率
θ^˙=γz1f1(x1)(2)\dot{\hat \theta}=\gamma z_1f_1(x_1) \qquad(2) θ^˙=γz1f1(x1)(2)
此时V˙2=−k1z12+z1z2\dot V_2=-k_1z_1^2+z_1z_2V˙2=−k1z12+z1z2,z1、z2z_1、z_2z1、z2为互连项。 -
考虑系统第二个误差的动态方程:
z˙2=x˙2−α˙1=u−α˙1\begin{aligned} \dot z_2&=\dot x_2-\dot \alpha_1\\ &=u-\dot \alpha_1 \end{aligned} z˙2=x˙2−α˙1=u−α˙1
值得注意的是此时α˙1\dot \alpha_1α˙1是一个关于x1,yd,y˙d,θ^x_1,y_d,\dot y_d,\hat \thetax1,yd,y˙d,θ^的复合函数,并且其中含有未知项,这也是上一篇文章所提到的问题。
α˙1=∂α∂x1x˙1+∂α∂ydy˙d+∂α∂y˙dy¨d+∂α∂θ^θ^˙=∂α∂x1(f1(x1)θ+x2)+∂α∂ydy˙d+∂α∂y˙dy¨d+∂α∂θ^θ^˙=∂α∂x1f1(x1)θ+∂α∂x1x2+∂α∂ydy˙d+∂α∂y˙dy¨d+∂α∂θ^θ^˙=wθ+ϕ\begin{aligned} \dot \alpha_1 &=\frac{\partial \alpha}{\partial x_1} \dot x_1+\frac{\partial \alpha}{\partial y_d} \dot y_d+\frac{\partial \alpha}{\partial \dot y_d} \ddot y_d+\frac{\partial \alpha}{\partial \hat \theta} \dot{\hat \theta}\\ &=\frac{\partial \alpha}{\partial x_1}(f_1(x_1)\theta+x_2)+\frac{\partial \alpha}{\partial y_d} \dot y_d+\frac{\partial \alpha}{\partial \dot y_d} \ddot y_d+\frac{\partial \alpha}{\partial \hat \theta} \dot{\hat \theta}\\ &=\frac{\partial \alpha}{\partial x_1}f_1(x_1)\theta+\frac{\partial \alpha}{\partial x_1}x_2+\frac{\partial \alpha}{\partial y_d} \dot y_d+\frac{\partial \alpha}{\partial \dot y_d} \ddot y_d+\frac{\partial \alpha}{\partial \hat \theta} \dot{\hat \theta}\\ &=w\theta+\phi \end{aligned} α˙1=∂x1∂αx˙1+∂yd∂αy˙d+∂y˙d∂αy¨d+∂θ^∂αθ^˙=∂x1∂α(f1(x1)θ+x2)+∂yd∂αy˙d+∂y˙d∂αy¨d+∂θ^∂αθ^˙=∂x1∂αf1(x1)θ+∂x1∂αx2+∂yd∂αy˙d+∂y˙d∂αy¨d+∂θ^∂αθ^˙=wθ+ϕ
其中令∂α∂x1f1(x1)=w\frac{\partial \alpha}{\partial x_1}f_1(x_1)=w∂x1∂αf1(x1)=w,∂α∂x1x2+∂α∂ydy˙d+∂α∂y˙dy¨d+∂α∂θ^θ^˙=ϕ\frac{\partial \alpha}{\partial x_1}x_2+\frac{\partial \alpha}{\partial y_d} \dot y_d+\frac{\partial \alpha}{\partial \dot y_d} \ddot y_d+\frac{\partial \alpha}{\partial \hat \theta} \dot{\hat \theta}=\phi∂x1∂αx2+∂yd∂αy˙d+∂y˙d∂αy¨d+∂θ^∂αθ^˙=ϕ,这两部分都是已知的。则:
z˙2=u−α˙1=u−wθ−ϕ\begin{aligned} \dot z_2 &=u-\dot \alpha_1\\ &=u-w\theta -\phi \end{aligned} z˙2=u−α˙1=u−wθ−ϕ -
考虑如下候选李雅普诺夫函数V3=V2+12z22V_3=V_2+\frac{1}{2}z_2^2V3=V2+21z22
对其求导得:
V˙3=V˙2+z2z˙2=−k1z12+z1z2+z2(u−wθ−ϕ)(3)\begin{aligned} \dot V_3&= \dot V_2+z_2\dot z_2\\ &=-k_1z_1^2+z_1z_2+z_2(u-w\theta -\phi) \end{aligned}\qquad(3) V˙3=V˙2+z2z˙2=−k1z12+z1z2+z2(u−wθ−ϕ)(3)
不知道看到公式(3),你有什么想法?我的想法则是估计过的参数怎么又出现了,这该怎么处理那?甚至有点后悔自己为什么那么早处理那个未知的参数,但是做到这个地方了,只能再次估计这个未知参数了。采用θ^2\hat \theta_2θ^2来估计θ\thetaθ。则引入新的估计误差θ~2=θ^2−θ\tilde \theta_2 =\hat \theta_2-\thetaθ~2=θ^2−θ. -
考虑新的候选李雅普诺夫函数V4=V3+12γ2θ~22V_4=V_3+\frac{1}{2\gamma_2}\tilde \theta_2^2V4=V3+2γ21θ~22
对其求导得:
V˙4=V˙3+1γ2θ~2θ^2˙=−k1z12+z1z2+z2(u−wθ−ϕ)+1γ2θ~2θ^2˙=−k1z12+z2(z1+u−wθ−ϕ)+1γ2θ~2θ^2˙(4)\begin{aligned} \dot V_4&= \dot V_3+\frac{1}{\gamma_2}\tilde \theta_2 \dot{\hat \theta_2}\\ &=-k_1z_1^2+z_1z_2+z_2(u-w\theta -\phi)+\frac{1}{\gamma_2}\tilde \theta_2 \dot{\hat \theta_2}\\ &=-k_1z_1^2+z_2(z_1+u-w\theta -\phi)+\frac{1}{\gamma_2}\tilde \theta_2 \dot{\hat \theta_2}\\ \end{aligned}\qquad(4) V˙4=V˙3+γ21θ~2θ^2˙=−k1z12+z1z2+z2(u−wθ−ϕ)+γ21θ~2θ^2˙=−k1z12+z2(z1+u−wθ−ϕ)+γ21θ~2θ^2˙(4) -
则依据公式(4),可以设计出控制率uuu
u=−k2z2−z1+ϕ+wθ^2(5)u=-k_2z_2-z_1+\phi+w\hat\theta_2 \qquad(5) u=−k2z2−z1+ϕ+wθ^2(5)
代入到(4)中,
V˙4=−k1z12+z2(z1+u−wθ−ϕ)+1γ2θ~2θ^2˙=−k1z12−k2z22+θ~2(z2w+1γθ^2˙)(6)\begin{aligned} \dot V_4 &=-k_1z_1^2+z_2(z_1+u-w\theta -\phi)+\frac{1}{\gamma_2}\tilde \theta_2 \dot{\hat \theta_2}\\ &=-k_1z_1^2-k_2z_2^2+\tilde \theta_2(z_2w+\frac{1}{\gamma}\dot{\hat \theta_2}) \end{aligned}\qquad(6) V˙4=−k1z12+z2(z1+u−wθ−ϕ)+γ21θ~2θ^2˙=−k1z12−k2z22+θ~2(z2w+γ1θ^2˙)(6) -
依据(6)可以设计出参数更新率为:
θ^2˙=−γ2z2w(7)\dot{\hat \theta_2}=-\gamma_2 z_2w\qquad(7) θ^2˙=−γ2z2w(7)
则公式(2)、(5)、(7)共同构成了系统的控制率和参数更新率。
小结
显然再不匹配条件下很离谱啊,一个未知参数按照在匹配条件下的做法设计,居然需要两个参数来估计,这显然是不合理的。假如这个系统是n阶的,那么就会需要n个估计参数来估计这一个不确定项,这就不可接受了。我们也自然而然地想到能不能将未知参数放到最后来一起处理那?有的,这叫做推迟参数设计。
接下来我们将通过推迟参数设计来重新设计上面这个系统的控制器和参数更新率。
2. 基于自适应反步控制和推迟参数设计的非匹配条件下的系统控制器设计
问题描述
仍旧针对公式(1)所代表的不匹配系统进行控制器设计,其中f1(x)f_1(x)f1(x)是已知的函数,θ\thetaθ为未知参数,设计控制器使得y→ydy→y_dy→yd,并且ydy_dyd的导数可知。
控制器设计
我们设计的步骤前面与“1. 基于自适应反步控制的非匹配条件下的系统控制器设计”的一致,一直到公式(*),即我们得到了
V˙2=−k1z12+z1z2+θ~(−z1f1(x1)+1γθ^˙)(∗∗)\begin{aligned} \dot V_2 &=-k_1z_1^2+z_1z_2+\tilde \theta(-z_1f_1(x_1)+\frac{1}{\gamma} \dot{\hat \theta}) \end{aligned}\qquad(**) V˙2=−k1z12+z1z2+θ~(−z1f1(x1)+γ1θ^˙)(∗∗)
但是在这个时候不设计参数更新率,直接考虑第二个误差的动态方程。
-
考虑系统第二个误差的动态方程:
z˙2=x˙2−α˙1=u−α˙1\begin{aligned} \dot z_2&=\dot x_2-\dot \alpha_1\\ &=u-\dot \alpha_1 \end{aligned} z˙2=x˙2−α˙1=u−α˙1
值得注意的是此时α˙1\dot \alpha_1α˙1是一个关于x1,yd,y˙d,θ^x_1,y_d,\dot y_d,\hat \thetax1,yd,y˙d,θ^的复合函数,并且其中含有未知项,这也是上一篇文章所提到的问题。
α˙1=∂α∂x1x˙1+∂α∂ydy˙d+∂α∂y˙dy¨d+∂α∂θ^θ^˙=∂α∂x1(f1(x1)θ+x2)+∂α∂ydy˙d+∂α∂y˙dy¨d+∂α∂θ^θ^˙=∂α∂x1f1(x1)θ+∂α∂x1x2+∂α∂ydy˙d+∂α∂y˙dy¨d+∂α∂θ^θ^˙=wθ+ψ+∂α∂θ^θ^˙\begin{aligned} \dot \alpha_1 &=\frac{\partial \alpha}{\partial x_1} \dot x_1+\frac{\partial \alpha}{\partial y_d} \dot y_d+\frac{\partial \alpha}{\partial \dot y_d} \ddot y_d+\frac{\partial \alpha}{\partial \hat \theta} \dot{\hat \theta}\\ &=\frac{\partial \alpha}{\partial x_1}(f_1(x_1)\theta+x_2)+\frac{\partial \alpha}{\partial y_d} \dot y_d+\frac{\partial \alpha}{\partial \dot y_d} \ddot y_d+\frac{\partial \alpha}{\partial \hat \theta} \dot{\hat \theta}\\ &=\frac{\partial \alpha}{\partial x_1}f_1(x_1)\theta+\frac{\partial \alpha}{\partial x_1}x_2+\frac{\partial \alpha}{\partial y_d} \dot y_d+\frac{\partial \alpha}{\partial \dot y_d} \ddot y_d+\frac{\partial \alpha}{\partial \hat \theta} \dot{\hat \theta}\\ &=w\theta+\psi+\frac{\partial \alpha}{\partial \hat \theta} \dot{\hat \theta} \end{aligned} α˙1=∂x1∂αx˙1+∂yd∂αy˙d+∂y˙d∂αy¨d+∂θ^∂αθ^˙=∂x1∂α(f1(x1)θ+x2)+∂yd∂αy˙d+∂y˙d∂αy¨d+∂θ^∂αθ^˙=∂x1∂αf1(x1)θ+∂x1∂αx2+∂yd∂αy˙d+∂y˙d∂αy¨d+∂θ^∂αθ^˙=wθ+ψ+∂θ^∂αθ^˙
其中令∂α∂x1f1(x1)=w\frac{\partial \alpha}{\partial x_1}f_1(x_1)=w∂x1∂αf1(x1)=w,∂α∂x1x2+∂α∂ydy˙d+∂α∂y˙dy¨d=ψ\frac{\partial \alpha}{\partial x_1}x_2+\frac{\partial \alpha}{\partial y_d} \dot y_d+\frac{\partial \alpha}{\partial \dot y_d} \ddot y_d=\psi∂x1∂αx2+∂yd∂αy˙d+∂y˙d∂αy¨d=ψ,这两部分都是已知的。则:
z˙2=u−α˙1=u−wθ−ψ−∂α∂θ^θ^˙\begin{aligned} \dot z_2 &=u-\dot \alpha_1\\ &=u-w\theta -\psi-\frac{\partial \alpha}{\partial \hat \theta} \dot{\hat \theta} \end{aligned} z˙2=u−α˙1=u−wθ−ψ−∂θ^∂αθ^˙ -
考虑如下候选李雅普诺夫函数V3=V2+12z22V_3=V_2+\frac{1}{2}z_2^2V3=V2+21z22
对其求导得:
V˙3=V˙2+z2z˙2=−k1z12+z1z2+θ~(−z1f1(x1)+1γθ^˙)+z2(u−wθ−ψ−∂α∂θ^θ^˙)=−k1z12+θ~(−z1f1(x1)+1γθ^˙)+z2(z1+u−wθ−ψ−∂α∂θ^θ^˙)(8)\begin{aligned} \dot V_3&= \dot V_2+z_2\dot z_2\\ &=-k_1z_1^2+z_1z_2+\tilde \theta(-z_1f_1(x_1)+\frac{1}{\gamma} \dot{\hat \theta})+z_2(u-w\theta -\psi-\frac{\partial \alpha}{\partial \hat \theta} \dot{\hat \theta})\\ &=-k_1z_1^2+\tilde \theta(-z_1f_1(x_1)+\frac{1}{\gamma} \dot{\hat \theta})+z_2(z_1+u-w\theta -\psi-\frac{\partial \alpha}{\partial \hat \theta} \dot{\hat \theta})\\ \end{aligned}\qquad(8) V˙3=V˙2+z2z˙2=−k1z12+z1z2+θ~(−z1f1(x1)+γ1θ^˙)+z2(u−wθ−ψ−∂θ^∂αθ^˙)=−k1z12+θ~(−z1f1(x1)+γ1θ^˙)+z2(z1+u−wθ−ψ−∂θ^∂αθ^˙)(8) -
则依据公式(8),可以设计出控制率uuu
u=−k2z2−z1+ψ+wθ^+∂α∂θ^θ^˙(9)u=-k_2z_2-z_1+\psi+w\hat\theta+\frac{\partial \alpha}{\partial \hat \theta} \dot{\hat \theta} \qquad(9) u=−k2z2−z1+ψ+wθ^+∂θ^∂αθ^˙(9)
代入到(8)中,
V˙3=−k1z12+θ~(−z1f1(x1)+1γθ^˙)+z2(z1+u−wθ−ψ−∂α∂θ^θ^˙)=−k1z12+θ~(−z1f1(x1)+1γθ^˙)+z2(z1+(−k2z2−z1+ψ+wθ^+∂α∂θ^θ^˙)−wθ−ψ−∂α∂θ^θ^˙)=−k1z12−k2z22+θ~(−z1f1(x1)+1γθ^˙)+z2wθ~=−k1z12−k2z22+θ~(−z1f1(x1)+1γθ^˙+z2w)(10)\begin{aligned} \dot V_3 &=-k_1z_1^2+\tilde \theta(-z_1f_1(x_1)+\frac{1}{\gamma} \dot{\hat \theta})+z_2(z_1+u-w\theta -\psi-\frac{\partial \alpha}{\partial \hat \theta} \dot{\hat \theta})\\ &=-k_1z_1^2+\tilde \theta(-z_1f_1(x_1)+\frac{1}{\gamma} \dot{\hat \theta})+z_2(z_1+(-k_2z_2-z_1+\psi+w\hat\theta+\frac{\partial \alpha}{\partial \hat \theta} \dot{\hat \theta})-w\theta -\psi-\frac{\partial \alpha}{\partial \hat \theta} \dot{\hat \theta})\\ &=-k_1z_1^2-k_2z_2^2+\tilde \theta(-z_1f_1(x_1)+\frac{1}{\gamma} \dot{\hat \theta})+z_2w \tilde \theta\\ &=-k_1z_1^2-k_2z_2^2+\tilde \theta(-z_1f_1(x_1)+\frac{1}{\gamma} \dot{\hat \theta}+z_2w) \end{aligned}\qquad(10) V˙3=−k1z12+θ~(−z1f1(x1)+γ1θ^˙)+z2(z1+u−wθ−ψ−∂θ^∂αθ^˙)=−k1z12+θ~(−z1f1(x1)+γ1θ^˙)+z2(z1+(−k2z2−z1+ψ+wθ^+∂θ^∂αθ^˙)−wθ−ψ−∂θ^∂αθ^˙)=−k1z12−k2z22+θ~(−z1f1(x1)+γ1θ^˙)+z2wθ~=−k1z12−k2z22+θ~(−z1f1(x1)+γ1θ^˙+z2w)(10) -
依据(10)可以设计出参数更新率为:
θ^˙=γ(z1f1(x1)−z2w)=γ(z1f1(x1)−z2∂α∂x1f1(x1))(11)\begin{aligned} \dot{\hat \theta}&= \gamma (z_1f_1(x_1)-z_2w)\\ &=\gamma (z_1f_1(x_1)-z_2\frac{\partial \alpha}{\partial x_1}f_1(x_1)) \end{aligned}\qquad(11) θ^˙=γ(z1f1(x1)−z2w)=γ(z1f1(x1)−z2∂x1∂αf1(x1))(11)
则公式(9)、(11)共同构成了系统的控制率和参数更新率。
小结
实际上推迟参数设计只是讲未知参数放到最后再进行处理,防止后续过程中再次出现未知参数。上述增加了推迟参数设计的过程中可以看到只用一个参数估计就可以解决非匹配条件下的控制系统,从而避免过参问题。
3. 基于自适应神经网络+反步控制+推迟参数设计的非匹配条件下的系统控制器设计
问题描述
x˙1=f(x1)+x2x˙2=uy=x1\begin{aligned} \dot x_1 &=f(x_1)+x_2\\ \dot x_2&=u\\ y&=x_1 \end{aligned} x˙1x˙2y=f(x1)+x2=u=x1
f1(x1)f_1(x_1)f1(x1) 是未知的光滑函数 ,设计设计控制器使得y→ydy→y_dy→yd,并且ydy_dyd的导数可知。
控制器设计
由前面设计自适应神经网络控制的经验可知,我们可以采用RBF神经网络估计f(x)f(x)f(x)
f(x1)=W∗TS(x1)+ϵ(x1)f(x_1)=W^{*T}S(x_1)+\epsilon (x_1) f(x1)=W∗TS(x1)+ϵ(x1)
其中W∗W^{*}W∗是理想的连接权值,S(x)S(x)S(x)是径向基函数,ϵ(x)\epsilon (x)ϵ(x)是逼近误差。
显然理想的连接权值我们也是无法直接获取的,因此也需要估计。设计W^\hat WW^为W∗W^*W∗的估计值,其误差表示为W~=W^−W∗\tilde W=\hat W-W^*W~=W^−W∗
那么接下来我们就能来继续设计控制器了。
-
定义系统误差:z1=y−yd=x1−ydz_1=y-y_d=x_1-y_dz1=y−yd=x1−yd
-
系统误差的动态方程:
z˙1=x˙1−y˙d=f1(x1)θ+x2−y˙d=W∗TS(x1)+ϵ(x1)+x2−y˙d\begin{equation} \begin{aligned} \dot z_1 &=\dot x_1 -\dot y_d\\ &=f_1(x_1) \theta+x_2-\dot y_d\\ &=W^{*T}S(x_1)+\epsilon (x_1)+x_2-\dot y_d\\ \end{aligned} \end{equation} z˙1=x˙1−y˙d=f1(x1)θ+x2−y˙d=W∗TS(x1)+ϵ(x1)+x2−y˙d -
考虑如下候选李亚普诺夫函数:V1=12z12+12W~TΓ−1W~V_1 = \frac{1}{2}z_1^2+\frac{1}{2}\tilde W^T \Gamma^{-1}\tilde WV1=21z12+21W~TΓ−1W~
对V1V_1V1进行求导:
V˙1=z1z˙1+Γ−1W~TW^˙=z1(W∗TS(x1)+ϵ(x1)+x2−y˙d)+Γ−1W~TW^˙(12)\begin{aligned} \dot V_1 &= z_1 \dot z_1+\Gamma^{-1}\tilde W^T\dot {\hat W}\\ &=z_1(W^{*T}S(x_1)+\epsilon (x_1)+x_2-\dot y_d)+\Gamma^{-1}\tilde W^T\dot {\hat W}\\ \end{aligned} \qquad(12) V˙1=z1z˙1+Γ−1W~TW^˙=z1(W∗TS(x1)+ϵ(x1)+x2−y˙d)+Γ−1W~TW^˙(12)
引入虚拟控制量α1\alpha_1α1,(大多数论文中都是应该直接引入虚拟控制量,而不会告诉你为什么这么做,这里也不再赘述了,上面也解释过了)令
α1=−k1z1−W^TS(x1)+y˙d\alpha_1=-k_1z_1-\hat W^TS(x_1)+\dot y_d α1=−k1z1−W^TS(x1)+y˙d
定义误差为:z2=x2−α1z_2=x_2-\alpha_1z2=x2−α1,代入公式(12),得:
V˙1=z1(W∗TS(x1)+ϵ(x1)+x2−y˙d)+Γ−1W~TW^˙=z1(W∗TS(x1)+ϵ(x1)+z2+α1−y˙d)+Γ−1W~TW^˙=z1(W∗TS(x1)+ϵ(x1)+z2+(−k1z1−W^TS(x1)+y˙d)−y˙d)+Γ−1W~TW^˙=−k1z12+z1z2−z1W~TS(x1)+z1ϵ(x1)+Γ−1W~TW^˙=−k1z12+z1z2+z1ϵ(x1)+W~T(Γ−1W^˙−z1S(x1))(13)\begin{aligned} \dot V_1 &=z_1(W^{*T}S(x_1)+\epsilon (x_1)+x_2-\dot y_d)+\Gamma^{-1}\tilde W^T\dot {\hat W}\\ &=z_1(W^{*T}S(x_1)+\epsilon (x_1)+z_2+\alpha_1-\dot y_d)+\Gamma^{-1}\tilde W^T\dot {\hat W}\\ &=z_1(W^{*T}S(x_1)+\epsilon (x_1)+z_2+(-k_1z_1-\hat W^TS(x_1)+\dot y_d)-\dot y_d)+\Gamma^{-1}\tilde W^T\dot {\hat W}\\ &=-k_1z_1^2+z_1z_2-z_1 \tilde W^TS(x_1)+z_1\epsilon(x_1)+\Gamma^{-1}\tilde W^T\dot {\hat W}\\ &=-k_1z_1^2+z_1z_2+z_1\epsilon(x_1)+\tilde W^T(\Gamma^{-1}\dot {\hat W}-z_1S(x_1)) \end{aligned} \qquad(13) V˙1=z1(W∗TS(x1)+ϵ(x1)+x2−y˙d)+Γ−1W~TW^˙=z1(W∗TS(x1)+ϵ(x1)+z2+α1−y˙d)+Γ−1W~TW^˙=z1(W∗TS(x1)+ϵ(x1)+z2+(−k1z1−W^TS(x1)+y˙d)−y˙d)+Γ−1W~TW^˙=−k1z12+z1z2−z1W~TS(x1)+z1ϵ(x1)+Γ−1W~TW^˙=−k1z12+z1z2+z1ϵ(x1)+W~T(Γ−1W^˙−z1S(x1))(13)
考虑推迟参数设计,暂时不对这里得参数进行参数更新率的设计。考虑第二个误差的动态方程:
z˙2=x˙2−α˙1=u−α˙1\begin{aligned} \dot z_2 &=\dot x_2 -\dot \alpha_1\\ &=u-\dot \alpha_1 \end{aligned} z˙2=x˙2−α˙1=u−α˙1
同样值得注意的是此时α˙1\dot \alpha_1α˙1是一个关于x1,yd,y˙d,W^x_1,y_d,\dot y_d,\hat Wx1,yd,y˙d,W^的复合函数,并且其中含有未知项。
α˙1=∂α∂x1x˙1+∂α∂ydy˙d+∂α∂y˙dy¨d+∂α∂W^W^˙=∂α∂x1(W∗TS(x1)+ϵ(x1)+x2)+∂α∂ydy˙d+∂α∂y˙dy¨d+∂α∂W^W^˙=∂α∂x1(W∗TS(x1)+ϵ(x1))+∂α∂x1x2+∂α∂ydy˙d+∂α∂y˙dy¨d+∂α∂W^W^˙=∂α∂x1W∗TS(x1)+∂α∂x1ϵ(x1)+ψ+∂α∂W^W^˙\begin{aligned} \dot \alpha_1 &=\frac{\partial \alpha}{\partial x_1} \dot x_1+\frac{\partial \alpha}{\partial y_d} \dot y_d+\frac{\partial \alpha}{\partial \dot y_d} \ddot y_d+\frac{\partial \alpha}{\partial \hat W} \dot{\hat W}\\ &=\frac{\partial \alpha}{\partial x_1}(W^{*T}S(x_1)+\epsilon (x_1)+x_2)+\frac{\partial \alpha}{\partial y_d} \dot y_d+\frac{\partial \alpha}{\partial \dot y_d} \ddot y_d+\frac{\partial \alpha}{\partial \hat W} \dot{\hat W}\\ &=\frac{\partial \alpha}{\partial x_1}(W^{*T}S(x_1)+\epsilon (x_1))+\frac{\partial \alpha}{\partial x_1}x_2+\frac{\partial \alpha}{\partial y_d} \dot y_d+\frac{\partial \alpha}{\partial \dot y_d} \ddot y_d+\frac{\partial \alpha}{\partial \hat W} \dot{\hat W}\\ &=\frac{\partial \alpha}{\partial x_1}W^{*T}S(x_1)+\frac{\partial \alpha}{\partial x_1}\epsilon (x_1)+\psi+\frac{\partial \alpha}{\partial \hat W} \dot{\hat W}\\ \end{aligned} α˙1=∂x1∂αx˙1+∂yd∂αy˙d+∂y˙d∂αy¨d+∂W^∂αW^˙=∂x1∂α(W∗TS(x1)+ϵ(x1)+x2)+∂yd∂αy˙d+∂y˙d∂αy¨d+∂W^∂αW^˙=∂x1∂α(W∗TS(x1)+ϵ(x1))+∂x1∂αx2+∂yd∂αy˙d+∂y˙d∂αy¨d+∂W^∂αW^˙=∂x1∂αW∗TS(x1)+∂x1∂αϵ(x1)+ψ+∂W^∂αW^˙
其中:∂α∂x1x2+∂α∂ydy˙d+∂α∂y˙dy¨d=ψ\frac{\partial \alpha}{\partial x_1}x_2+\frac{\partial \alpha}{\partial y_d} \dot y_d+\frac{\partial \alpha}{\partial \dot y_d} \ddot y_d=\psi∂x1∂αx2+∂yd∂αy˙d+∂y˙d∂αy¨d=ψ是已知的。则对应的z˙2=u−∂α∂x1W∗TS(x1)−∂α∂x1ϵ(x1)−ψ−∂α∂W^W^˙\dot z_2=u-\frac{\partial \alpha}{\partial x_1}W^{*T}S(x_1)-\frac{\partial \alpha}{\partial x_1}\epsilon (x_1)-\psi-\frac{\partial \alpha}{\partial \hat W} \dot{\hat W}z˙2=u−∂x1∂αW∗TS(x1)−∂x1∂αϵ(x1)−ψ−∂W^∂αW^˙。
-
考虑新的李雅普诺夫函数:V2=V1+12z22V_2=V_1+\frac{1}{2}z_2^2V2=V1+21z22
对其求导得:
V˙2=V˙1+z2z˙2=−k1z12+z1z2+z1ϵ(x1)+W~T(Γ−1W^˙−z1S(x1))+z2(u−∂α∂x1W∗TS(x1)−∂α∂x1ϵ(x1)−ψ−∂α∂W^W^˙)=−k1z12+z1ϵ(x1)+W~T(Γ−1W^˙−z1S(x1))+z2(z1+u−∂α∂x1W∗TS(x1)−∂α∂x1ϵ(x1)−ψ−∂α∂W^W^˙)(14)\begin{aligned} \dot V_2&= \dot V_1+z_2 \dot z_2\\ &=-k_1z_1^2+z_1z_2+z_1\epsilon(x_1)+\tilde W^T(\Gamma^{-1}\dot {\hat W}-z_1S(x_1))+z_2(u-\frac{\partial \alpha}{\partial x_1}W^{*T}S(x_1)-\frac{\partial \alpha}{\partial x_1}\epsilon (x_1)-\psi-\frac{\partial \alpha}{\partial \hat W} \dot{\hat W})\\ &=-k_1z_1^2+z_1\epsilon(x_1)+\tilde W^T(\Gamma^{-1}\dot {\hat W}-z_1S(x_1))+z_2(z_1+u-\frac{\partial \alpha}{\partial x_1}W^{*T}S(x_1)-\frac{\partial \alpha}{\partial x_1}\epsilon (x_1)-\psi-\frac{\partial \alpha}{\partial \hat W} \dot{\hat W})\\ \end{aligned} \qquad(14) V˙2=V˙1+z2z˙2=−k1z12+z1z2+z1ϵ(x1)+W~T(Γ−1W^˙−z1S(x1))+z2(u−∂x1∂αW∗TS(x1)−∂x1∂αϵ(x1)−ψ−∂W^∂αW^˙)=−k1z12+z1ϵ(x1)+W~T(Γ−1W^˙−z1S(x1))+z2(z1+u−∂x1∂αW∗TS(x1)−∂x1∂αϵ(x1)−ψ−∂W^∂αW^˙)(14)
针对公式(14)可以设计控制器uuu
u=−k2z2−z1+∂α∂x1W^TS(x1)+ψ+∂α∂W^W^˙(15)u=-k_2z_2-z_1+\frac{\partial \alpha}{\partial x_1}\hat W^{T}S(x_1)+\psi+\frac{\partial \alpha}{\partial \hat W} \dot{\hat W} \qquad(15) u=−k2z2−z1+∂x1∂αW^TS(x1)+ψ+∂W^∂αW^˙(15)
将公式(15)代入到公式(14)中去:
V˙2=−k1z12+z1ϵ(x1)+W~T(Γ−1W^˙−z1S(x1))+z2(z1+u−∂α∂x1W∗TS(x1)−∂α∂x1ϵ(x1)−ψ−∂α∂W^W^˙)=−k1z12−k2z22+z1ϵ(x1)+W~T(Γ−1W^˙−z1S(x1))+z2(∂α∂x1W~TS(x1)−∂α∂x1ϵ(x1))=−k1z12−k2z22+W~T(Γ−1W^˙−z1S(x1)+z2∂α∂x1S(x1))+ϵ(x1)(z1−z2∂α∂x1)(16)\begin{aligned} \dot V_2&=-k_1z_1^2+z_1\epsilon(x_1)+\tilde W^T(\Gamma^{-1}\dot {\hat W}-z_1S(x_1))+z_2(z_1+u-\frac{\partial \alpha}{\partial x_1}W^{*T}S(x_1)-\frac{\partial \alpha}{\partial x_1}\epsilon (x_1)-\psi-\frac{\partial \alpha}{\partial \hat W} \dot{\hat W})\\ &=-k_1z_1^2-k_2z_2^2+z_1\epsilon(x_1)+\tilde W^T(\Gamma^{-1}\dot {\hat W}-z_1S(x_1))+z_2(\frac{\partial \alpha}{\partial x_1}\tilde W^{T}S(x_1)-\frac{\partial \alpha}{\partial x_1}\epsilon (x_1))\\ &=-k_1z_1^2-k_2z_2^2+\tilde W^T(\Gamma^{-1}\dot {\hat W}-z_1S(x_1)+z_2\frac{\partial \alpha}{\partial x_1}S(x_1))+\epsilon(x_1)(z_1-z_2\frac{\partial \alpha}{\partial x_1}) \end{aligned} \qquad(16) V˙2=−k1z12+z1ϵ(x1)+W~T(Γ−1W^˙−z1S(x1))+z2(z1+u−∂x1∂αW∗TS(x1)−∂x1∂αϵ(x1)−ψ−∂W^∂αW^˙)=−k1z12−k2z22+z1ϵ(x1)+W~T(Γ−1W^˙−z1S(x1))+z2(∂x1∂αW~TS(x1)−∂x1∂αϵ(x1))=−k1z12−k2z22+W~T(Γ−1W^˙−z1S(x1)+z2∂x1∂αS(x1))+ϵ(x1)(z1−z2∂x1∂α)(16)
-
根据公式(16)可以设计出参数更新率为:
W^˙=Γ(z1S(x1)−z2∂α∂x1S(x1))(17)\dot {\hat W}=\Gamma(z_1S(x_1)-z_2\frac{\partial \alpha}{\partial x_1}S(x_1)) \qquad(17) W^˙=Γ(z1S(x1)−z2∂x1∂αS(x1))(17)
则对应的V˙2\dot V_2V˙2为:
V˙2=−k1z12−k2z22+ϵ(x1)(z1−z2∂α∂x1)(18)\begin{aligned} \dot V_2 &=-k_1z_1^2-k_2z_2^2+\epsilon(x_1)(z_1-z_2\frac{\partial \alpha}{\partial x_1}) \end{aligned} \qquad(18) V˙2=−k1z12−k2z22+ϵ(x1)(z1−z2∂x1∂α)(18)
之后再对ϵ(x1)(z1−z2∂α∂x1)\epsilon(x_1)(z_1-z_2\frac{\partial \alpha}{\partial x_1})ϵ(x1)(z1−z2∂x1∂α)进行放缩就可以完成控制器的设计了。至此公式(15)和公式(17)共同构成系统的控制器和参数更新率。
小结
本小节的内容综合了反步设计(Backstepping)、自适应神经网络控制(ANC)和推迟参数设计,利用他们共同设计了控制器和参数更新率。
总结
本文主要针对非匹配条件下的系统,利用自适应反步控制和自适应神经网络来设计控制器和参数更新率。读者在阅读了前面几篇文章的基础上,相信会有所收获。
如果您觉得我写的不错,麻烦给我一个免费的赞!如果内容中有错误,也欢迎向我反馈。
相关文章:

推迟参数设计的自适应反步控制和自适应神经网络的反步控制设计
推迟参数设计的自适应反步控制和自适应神经网络的反步控制设计 目录推迟参数设计的自适应反步控制和自适应神经网络的反步控制设计前言匹配与非匹配1. 基于自适应反步控制的非匹配条件下的系统控制器设计问题描述控制器设计小结2. 基于自适应反步控制和推迟参数设计的非匹配条件…...

spring5.1+SmartInstantiationAwareBeanPostProcessor 解决循环依赖
SmartInstantiationAwareBeanPostProcessor 解决循环依赖的过程, 例如上面的 A依赖B, B依赖A SmartInstantiationAwareBeanPostProcessor 是 Spring 中的一个接口,它扩展了 InstantiationAwareBeanPostProcessor 接口并提供了对 Bean 的实例化和属性填充的更高级的…...

apply、call与bind
共同点: 都是函数对象的一个方法,作用是改变函数执行时的上下文,即改变函数体内部this的指向 var name "lucy"; var obj {name: "martin",say: function () {console.log(this.name);} }; obj.say(); // martin&…...

《Effective Objective-C 2.0 》 阅读笔记 item3
第3条:多用字面量语法,少用与之等价的方法 1. 字面数值 使用字面量能令代码更为简洁: NSNumber *someNumber 1; *** 字面量语法的好处! *** 令代码更为简洁。能够以NSNumber实例表示的所有数据类型(int、float、d…...

SSL/TLS 证书管理
SSL 证书发现 随着组织的 IT 基础架构的扩展,他们为每台计算机获取证书以保护其资源和域。此外,开发人员通常会创建许多自签名证书,以便在产品的开发阶段保护内部网络。组织通常最终会拥有数千个证书。自动发现证书提供了对证书基础结构的完…...
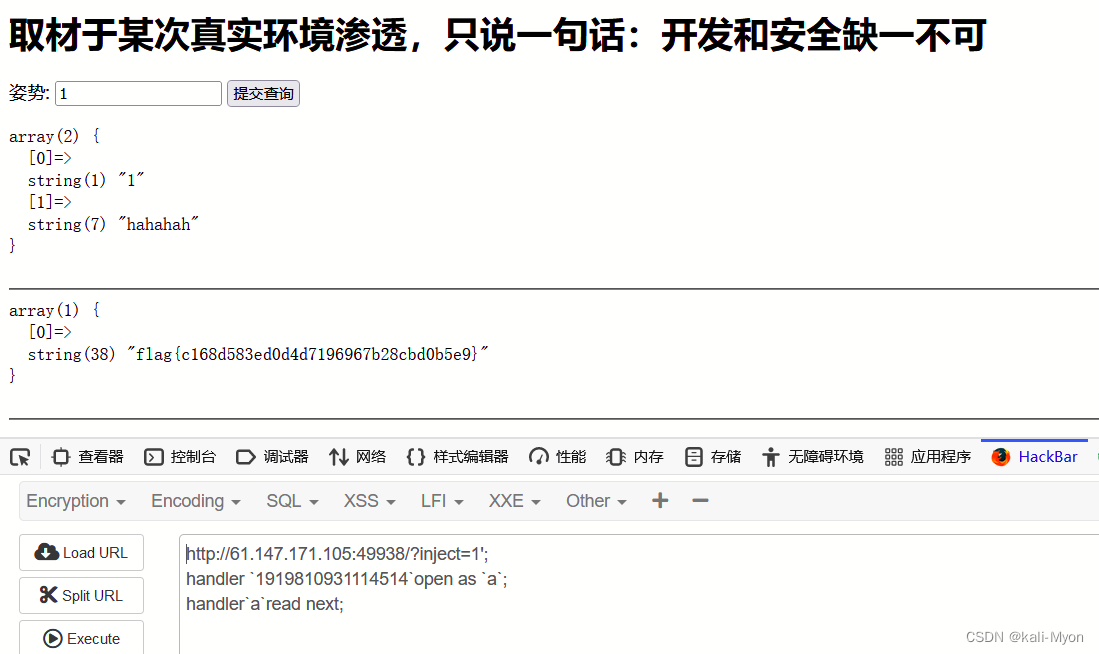
supersqli(SQL注入流程及常用SQL语句)
目录 一、SQL注入知识学习 1、判断注入类型 (1)数字型注入判断 (2)字符型注入判断 2、猜解sql查询语句中的字段数(order by 的使用) 3、判断显示位爆数据库的名字 4、注释(--的使用&#…...

【数据结构】用Java实现一棵二叉树
目录 前言 1. 创建MyBinaryTree类 2. 从前序与中序遍历序列构造二叉树 3. 从中序与后序遍历序列构造二叉树 4. 用层序遍历验证二叉树是否构建成功 5. 整体代码(构建二叉树、二叉树的基本功能和测试代码) 6. 测试结果 前言 前面两篇文章已经给出了…...
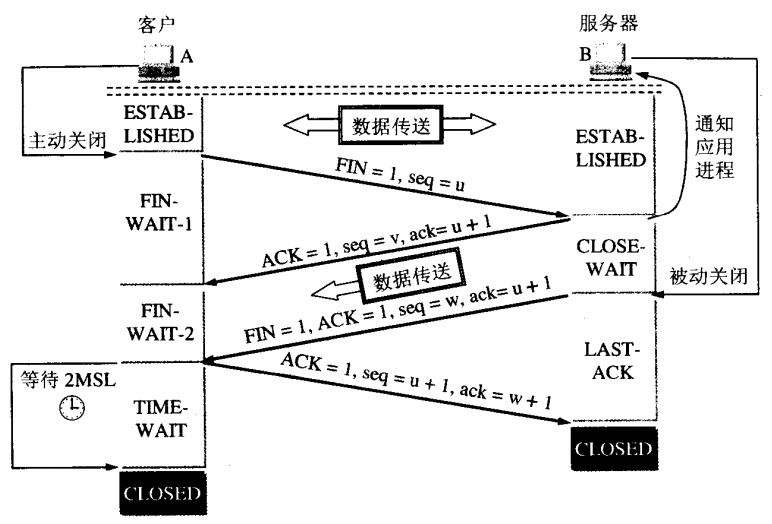
【面试】面试官问的几率较大的网络安全面试题
文章目录防范常见的 Web 攻击1、什么是SQL注入攻击2、什么是XSS攻击3、什么是CSRF攻击4、什么是文件上传漏洞5、DDos 攻击重要协议分布图1、arp协议的工作原理ARP协议工作原理:2、什么是RARP?工作原理3、dns是什么?dns的工作原理4、rip协议是…...

[Python] 循环语句
循环语句就是在符合条件的情况下,重复执行一个代码段 1.while循环 while语句可用于在条件为真时反复执行代码块 语法格式 while 条件语句:执行语句 当条件语句为真(True)时,就会执行while循环下的语句 示例 实现1到100 的累加并输出求和结果 …...
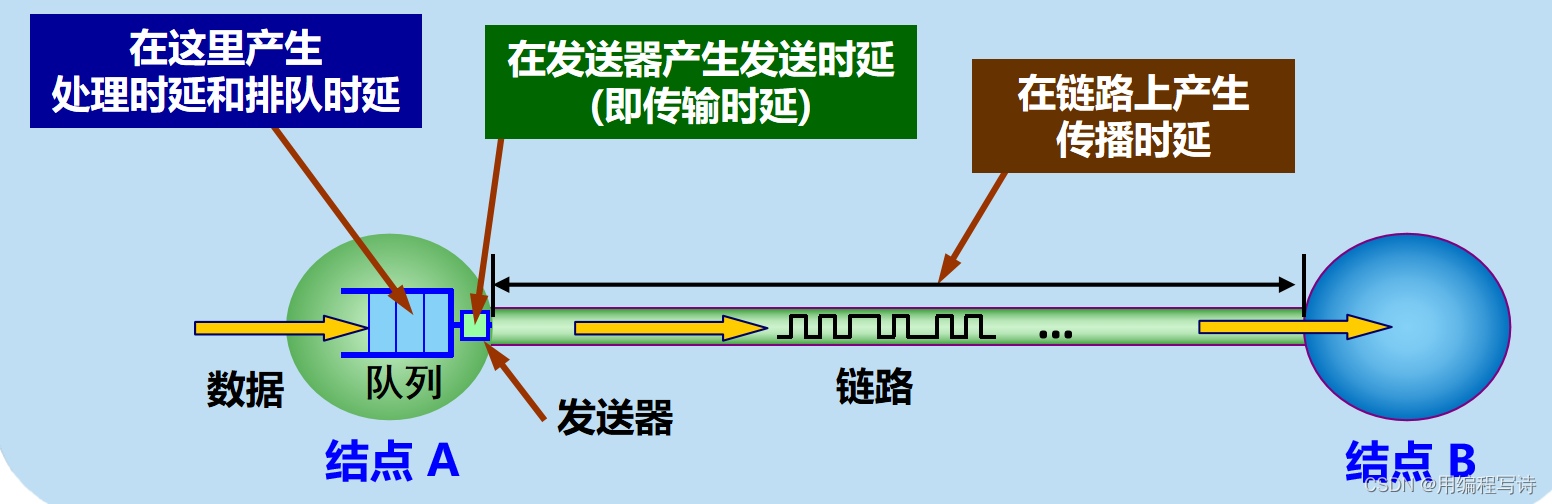
计算机网络考试复习——第一章 1.5 1.6
1.5 计算机网络的类别 1.5.1计算机网络的定义: 系统集合,连接起来,协议工作,资源共享 计算机网络主要是由一些通用的、可编程的硬件互连而成的,而这些硬件并非专门用来实现某一特定目的(例如࿰…...

3.29 最小生成树算法
最小生成树概念 参考:什么是最小生成树? Minimum Spanning Tree 何为生成树? 生成树是指一个联通图的极小的连通子图,它包含了图中的所有n个顶点,并只有n-1条边(构成一棵树) 生成树的一些性…...

计算机科班与培训开发编程的区别在哪里?
科班、培训班、科班培训班的模式都培养了很多编程技术人员进入IT行业,有的成为某个技术领域的专家,有的成为领导层,有的一直在默默无闻的敲代码等待35岁的到来。不管那种方式入行,这些类似的情况都存在,并且未来还会一…...

idea设置常用自设置快捷键及坐标
<!--mybatis 依赖--> <dependency> <groupId>org.mybatis</groupId> <artifactId>mybatis</artifactId> <version>3.5.5</version> </dependency…...

Vue 3.0 实例方法
#$watch 参数:{string | Function} source{Function | Object} callback{Object} [options] {boolean} deep{boolean} immediate{string} flush返回:{Function} unwatch用法: 侦听组件实例上的响应式 property 或函数计算结果的变化。回调函数…...

日撸 Java 三百行day1-10
文章目录说明day1 环境搭建1.1 开发环境1.2 package import 和 println1.3 编写HelloWorld.javaday2 基本算术操作2.1 加、减、乘、除、整除、取余.day3 基本if 语句3.1 if条件分支语句3.2 代码day4 闰年的计算4.1 思路整理:何为闰年?4.2 核心代码day5 基…...
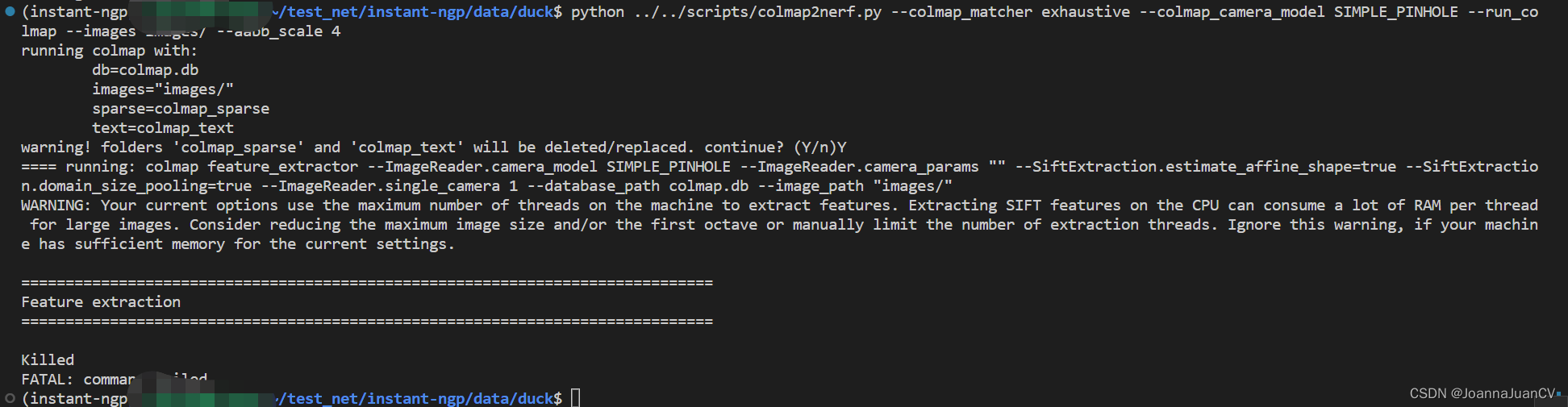
Ubuntu Instant-ngp 训练自有数据集
1. 运行环境配置 conda create -n instant-ngp python3.10 conda activate instant-ngp pip install -r requirements.txt -i https://pypi.tuna.tsinghua.edu.cn/simple2. COLMAP稀疏重建生成transform.json colmap 环境配置参考文档; 终端定位在instant-ngp/da…...

k8s集群只一台节点,重启节点后命名空间找不到了
定位 如果您的Kubernetes集群只有一台节点,并且在重启节点之前您创建了一些命名空间和资源,那么在节点重启后,这些命名空间和资源可能会丢失。这是因为在Kubernetes中,资源和命名空间通常是存储在etcd中的。当节点重启时…...
MarkDown示例
这里写自定义目录标题欢迎使用Markdown编辑器新的改变功能快捷键合理的创建标题,有助于目录的生成如何改变文本的样式插入链接与图片如何插入一段漂亮的代码片生成一个适合你的列表创建一个表格设定内容居中、居左、居右SmartyPants创建一个自定义列表如何创建一个注…...

spring cloud 雪崩效应
什么是雪崩效应 雪崩就是塌方。在山坡上的积雪,如果积雪的内聚力小于重力或其他力量,则积雪便向下滑动,从而逐渐引起积雪的崩塌。 在微服务架构中,服务之间通常存在级联调用。比如,服务A调用服务B,而服…...

Python 自动化指南(繁琐工作自动化)第二版:三、函数
原文:https://automatetheboringstuff.com/2e/chapter3/ 您已经熟悉了前几章中的print()、input()和len()函数。Python 提供了几个这样的内置函数,但是您也可以编写自己的函数。函数就像一个程序中的一个小程序。 为了更好地理解函数是如何工作的&#…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...

从实验室到产业:IndexTTS 在六大核心场景的落地实践
一、内容创作:重构数字内容生产范式 在短视频创作领域,IndexTTS 的语音克隆技术彻底改变了配音流程。B 站 UP 主通过 5 秒参考音频即可克隆出郭老师音色,生成的 “各位吴彦祖们大家好” 语音相似度达 97%,单条视频播放量突破百万…...

leetcode_69.x的平方根
题目如下 : 看到题 ,我们最原始的想法就是暴力解决: for(long long i 0;i<INT_MAX;i){if(i*ix){return i;}else if((i*i>x)&&((i-1)*(i-1)<x)){return i-1;}}我们直接开始遍历,我们是整数的平方根,所以我们分两…...

CppCon 2015 学习:REFLECTION TECHNIQUES IN C++
关于 Reflection(反射) 这个概念,总结一下: Reflection(反射)是什么? 反射是对类型的自我检查能力(Introspection) 可以查看类的成员变量、成员函数等信息。反射允许枚…...
