【AGC005D】~K Perm Counting(计数抽象成图)
容斥原理。
求出f(m) ,f(m)指代至少有m个位置不合法的方案数。
怎么求?
注意到位置为id,权值为v ,不合法的情况,当且仅当 v = id+k或 v= id-k
因此,我们把每一个位置和权值抽象成点 ,不合法的情况之间连一条边,可以构成二分图。
借用大佬的图。
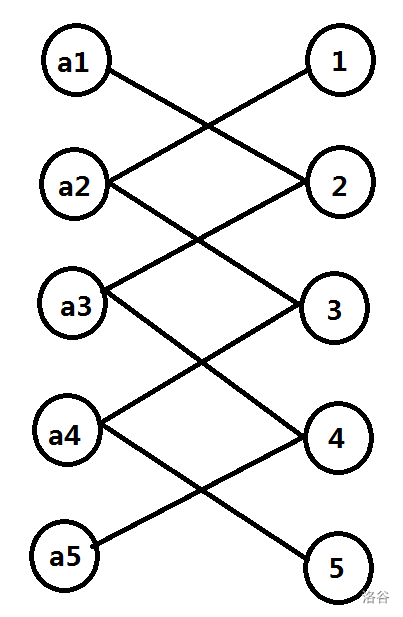
由此可知,当选了n条边,就恰好n个位置不合法,限制条件是:连的边不能相邻,
把二分图展开成k条链,进行dp。
还是借用大佬ez_lcw的图

由此总共有2n 个点 k 条链,链与链之间无边 互不干涉。
dp(i,j,pd)表示考虑到第i号点, 连了j条边,是否有连接i 到 i-1号点。
转移方程
则可得
简单的乘法原理罢了。
#include<bits/stdc++.h>
using namespace std;
long long n,k;
long long fac[4010];
long long dp[4010][4010][2];
int mod = 1e9+7;
int pd[4999];//判断是否为链头 0 表示是头 头不能连接上一个
int main(){freopen("neverk.in","r",stdin);freopen("neverk.out","w",stdout);cin>>n>>k;fac[0] = 1;for(int i = 1;i <= n;i++){fac[i] = (fac[i-1]*(long long)i)%mod;}int tot = 0;for(int i=1;i<=k;i++){for(int t=0;t<2;t++){for(int j=i;j<=n;j+=k){tot++;if(i!=j) pd[tot]=1;}}}dp[0][0][0] = 1;for(int i = 1;i <= 2*n;i++){for(int j = 0;j <= n;j++){dp[i][j][0] = (dp[i-1][j][0] + dp[i-1][j][1])%mod;if(j&&pd[i]) dp[i][j][1] = dp[i-1][j-1][0];}}long long cnt = 0;for(int i = 0;i <= n;i++){//cout<<fac[n-i]<<" "<<dp[2*n][i][0]+dp[2*n][i][1]<<endl;long long t = fac[n-i]*(dp[2*n][i][0]+dp[2*n][i][1]);t%=mod;//cout<<t<<endl;if(i%2 == 0){cnt = (cnt +t)%mod;}else{cnt = (cnt - t + mod)%mod;}}cout<<cnt;return 0;
}相关文章:
【AGC005D】~K Perm Counting(计数抽象成图)
容斥原理。 求出f(m) ,f(m)指代至少有m个位置不合法的方案数。 怎么求? 注意到位置为id,权值为v ,不合法的情况,当且仅当 v idk或 v id-k 因此,我们把每一个位置和权值抽象成点 ,不合法的情况之间连一…...
 是怎么记住上一个状态值的?)
【React】setState (useState) 是怎么记住上一个状态值的?
在 React 中,setState 通过 React 内部的状态管理机制来记住上一个状态值。即使每次组件重新渲染时,函数组件会被重新执行,React 仍能通过其内部的状态管理系统保持和追踪组件的状态变化。下面详细解释其工作原理: 1. setState 的…...

Vue3 使用CryptoJS加密
为什么要加密? 现在的互联网世界充满了各种各样的信息,有些信息非常重要,比如密码、个人信息等。如果我们把这些信息直接发送到服务器,别人可能会截取到,然后偷走我们的信息。为了避免这种情况发生,我们需…...

Feign的使用
一、Feign 介绍 Feign 是一个声明式的 HTTP 客户端,它使得编写 HTTP 客户端变得更加简单。在微服务架构中,使用 Feign 可以轻松地调用其他服务。Feign 内置了 Ribbon 实现负载均衡。 二、Feign 的使用步骤 引入依赖: 在项目的 pom.xml 文件…...

前端反接保护:实用方案解析与探讨
前端反接保护通常采用肖特基二极管方案或PMOS/NMOS方案,本文另外介绍一种理想二极管方案。 1、肖特基二极管方案 由于肖特基二极管具有正向导通电压,只能用于小电流场合,甚至于直接使用普通的整流二极管。比如1A电流,设D1的正向…...

【C++】第五节:内存管理
1、C/C内存分布 看下面一段代码 int globalVar 1; static int staticGlobalVar 1; void Test() {static int staticVar 1;int localVar 1;int num1[10] { 1, 2, 3, 4 };char char2[] "abcd";const char* pChar3 "abcd";int* ptr1 (int*)malloc(s…...

【Java SE】方法 和 递归 的应用
🔥博客主页🔥:【 坊钰_CSDN博客 】 欢迎各位点赞👍评论✍收藏⭐ 目录 1. 方法的含义 1.1 例子 1.2 方法的概念 2. 方法的定义 3. 实参和形参 3.1 实参和形参的关系 4. 方法的重载 5. 递归 5.1 递归练习 6. 小结 1. 方法的…...
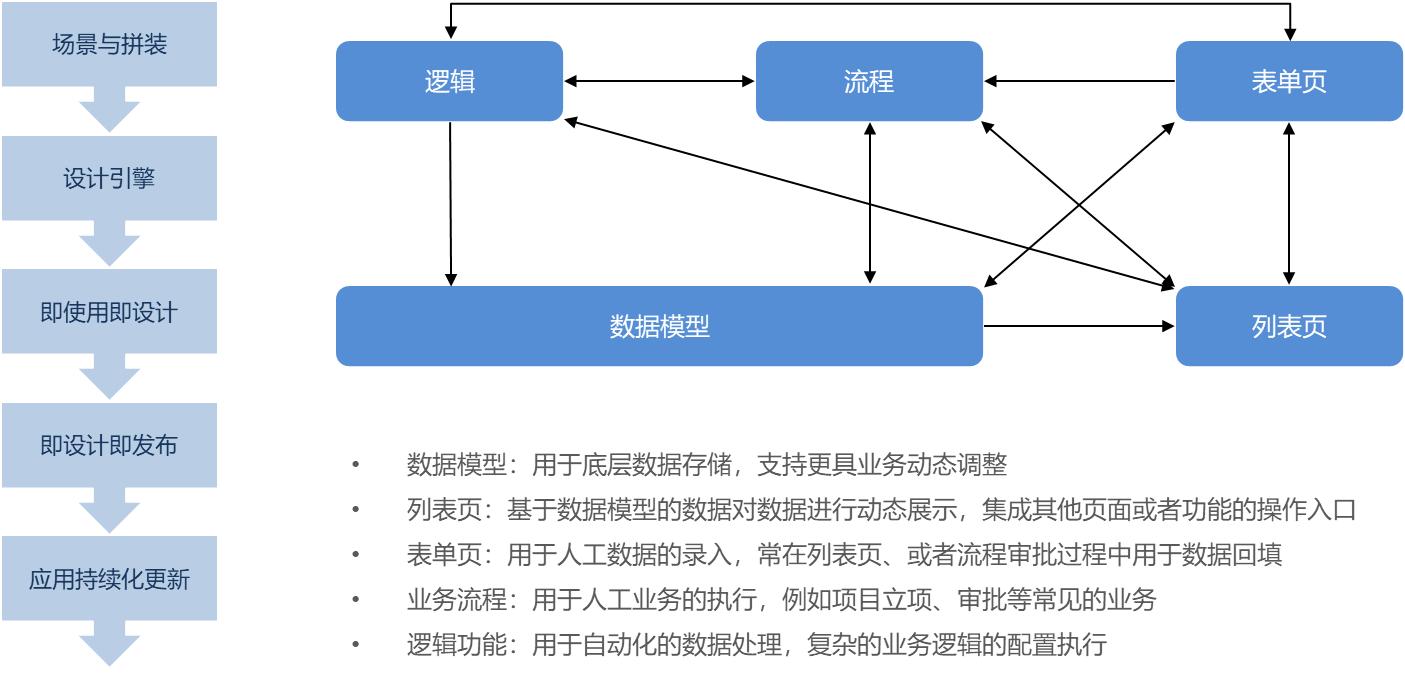
JVS低代码轻应用是什么?是如何拼装的?这篇文章讲的非常详细
1.1JVS轻应用是什么? 轻应用与传统应用的开发过程区别 传统开发(原生开发)采用的方式:①需求了解 ②产品原型③UI设计④建库建表⑤前端还原⑥后端开发⑦前后端联调⑧功能测试⑨部署上线轻应用开发方式(配置化拼装&…...
与STM32 通信教程)
K210(openMV)与STM32 通信教程
目录 前言: 一、K210 串口部分教程 二、STM32部分 前言: 很多打比赛的同学,通常只是用K210 或者openMV来进行视觉部分的信息采集,传输数据给STM32(或者其他主控那边)进行对分析,对小车或者舵…...
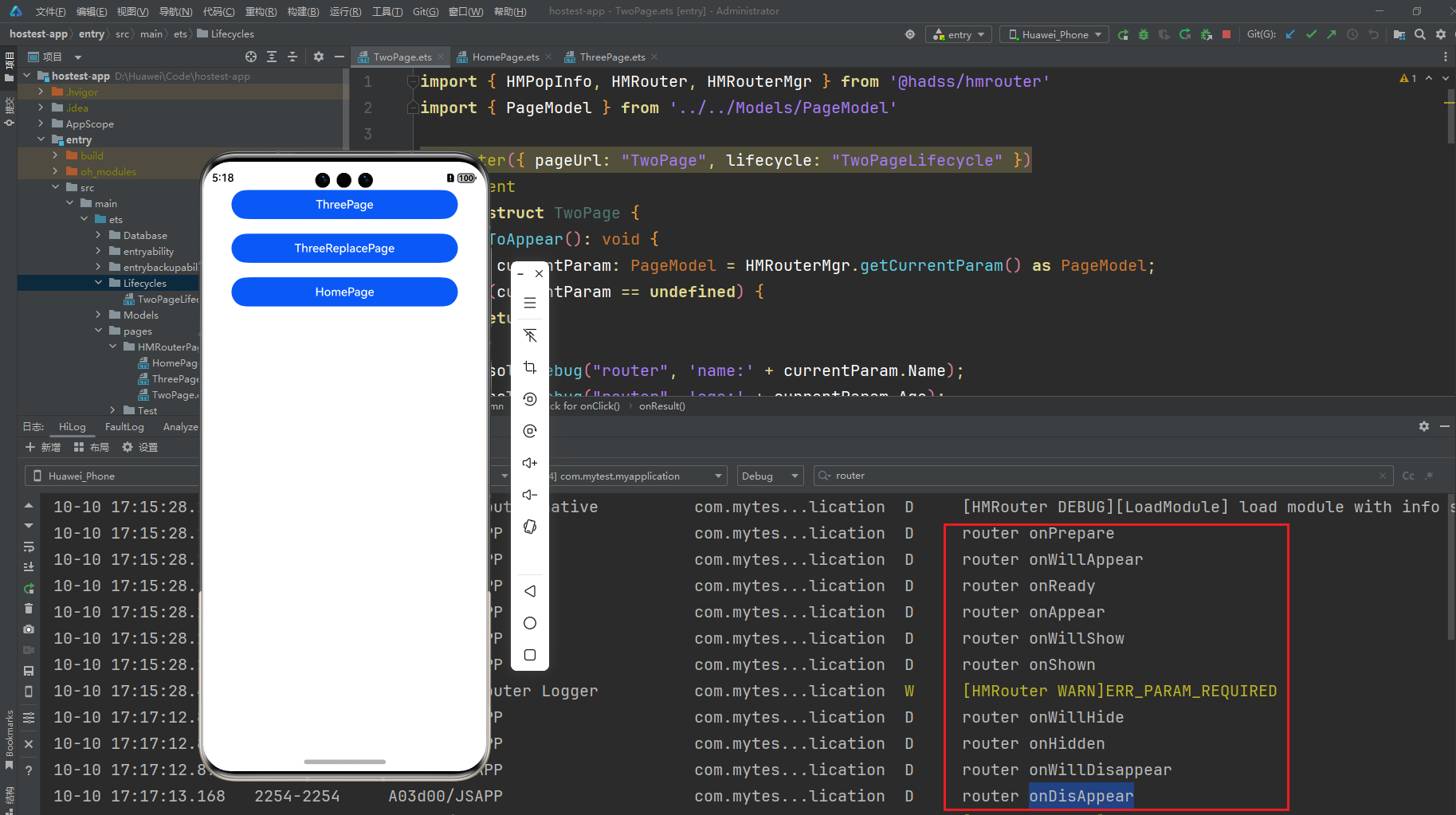
【HarmonyOS】HMRouter使用详解(三)生命周期
生命周期(Lifecycle) 使用HMRouter的页面跳转时,想实现和Navigation一样的生命周期时,需要通过新建生命周期类来实现对页面对某一个生命周期的监控。 新建Lifecycle类 通过继承IHMLifecycle接口实现生命周期接口的方法重写。 通过…...
)
Docker 教程三 (Ubuntu Docker安装)
Ubuntu Docker 安装 Docker Engine-Community 支持以下的 Ubuntu 版本: Xenial 16.04 (LTS)Bionic 18.04 (LTS)Cosmic 18.10Disco 19.04 其他更新的版本…… Docker Engine - Community 支持上 x86_64(或 amd64)armhf,arm64&am…...

Redis:持久化
Redis:持久化 持久化RDBdump.rdb优缺点 AOF文件同步重写机制 混合持久化 持久化 虽然Redis是一个内存级别的数据库,但是Redis也是有持久化的能力的。当系统崩溃时,Redis就会被强制退出,此时内存中的数据就会丢失。为了能够在下次…...

精准监控,高效运营 —— 商品信息实时分析为商家带来新机遇
在现代商业环境中,精准监控和高效运营是商家成功的关键。通过实时分析商品信息,商家可以洞察市场趋势、优化库存管理、提升销售策略,从而抓住新的商业机遇。本文将介绍如何利用Python和一些流行的数据分析工具来实现商品信息的实时分析&#…...

Nginx应用配置实战
Nginx通用部署 Nginx常见参数介绍 Nginx 配置文件中的指令和参数决定了它的行为。下面详细介绍一些常见的 Nginx 参数,以帮助你更好地理解和配置 Nginx。 1. worker_processes worker_processes auto;作用:设置 Nginx 处理请求的工作进程数量。auto …...

html实现倒计时
参考网址 <!DOCTYPE html> <html> <head><title>倒计时示例</title> </head> <body><h1 id"titleCountDown"></h1><div id"countdown"></div><script>// 目标日期var targetDat…...

HTMLCSS练习
1) 效果如下 2) 代码如下 2.1) HTML <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name"viewport" conte…...

LeetCode讲解篇之377. 组合总和 Ⅳ
文章目录 题目描述题解思路题解代码题目链接 题目描述 题解思路 总和为target的元素组合个数 可以由 总和为target - nums[j]的元素组合个数 转换而来,其中j为nums所有元素的下标 而总和target - nums[j]的元素组合个数 可以由 总和为target - nums[j] - nums[k]的…...

Midjourney中文版:创意无限,艺术之旅由此启程
Midjourney中文版——一个将你的文字想象转化为视觉艺术的神奇平台。无需繁琐的绘画技巧,只需简单的文字描述,你就能开启一场前所未有的艺术之旅。 Midjourney AI超强绘画 (原生态系统)用户端:Ai Loadinghttps://www.mjdiscord.c…...

安装R和RStudio:开始你的数据分析之旅
数据分析是当今世界中一个非常热门的领域,而R语言是进行数据分析的强大工具之一。R是一种编程语言和软件环境,用于统计计算和图形表示。RStudio是一个集成开发环境(IDE),它为R语言提供了一个更加友好和高效的工作环境。…...

如何使用python连接数据库?
数据分析离不开数据库,如何使用python连接数据库呢?听我娓娓道来哈 该笔记参考了PyMySQL官方文档和《python数据采集》关于数据存储的部分,欢迎大家去阅读原著,相信会理解的更加透彻。 补充:文末增加Oracle数据库的连…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...
