程序设计基础I-实验7 函数(编程题)
7-1 sdut- C语言实验—计算表达式
计算下列表达式值:
![]()
输入格式:
输入x和n的值,其中x为非负实数,n为正整数。
输出格式:
输出f(x,n),保留2位小数。
输入样例:
3 2
输出样例:
在这里给出相应的输出。例如:
2.00#include<stdio.h>
#include<math.h>
double f(double x,int n)
{if(n==1)return sqrt(1+x);elsereturn sqrt(n+f(x,n-1));
}
int main()
{double x;int n;scanf("%lf %d",&x,&n);printf("%.2f",f(x,n));return 0;
}7-2 求组合数
本题要求编写程序,根据公式Cnm=m!(n−m)!n!算出从n个不同元素中取出m个元素(m≤n)的组合数。
建议定义和调用函数fact(n)计算n!,其中n的类型是int,函数类型是double。
输入格式:
输入在一行中给出两个正整数m和n(m≤n),以空格分隔。
输出格式:
按照格式“result = 组合数计算结果”输出。题目保证结果在double类型范围内。
输入样例:
2 7
输出样例:
result = 21#include<stdio.h>
double fact(int n)
{int i;double sum=1;for(i=1;i<=n;i++){sum=sum*i;}return sum;
}
int main()
{int m,n;double t;scanf("%d %d",&m,&n);t=fact(n)/(fact(m)*fact(n-m));printf("result = %.lf",t);return 0;
}7-3 求算式的和[1]
定义函数main(),输入正整数n,计算并输出下列算式的值。要求调用函数f(n)计算n*(n+1)…(2n-1),函数返回值类型是double。
s=1+2∗31+3∗4∗51+......+n∗(n+1)∗...∗(2n−1)1
输入格式:
输入在一行中给出一个正整数n。
输出格式:
在一行中按照“sum = S”的格式输出部分和的值S,精确到小数点后六位,请注意等号的左右各有一个空格。题目保证计算结果不超过双精度范围。
输入样例:
3
输出样例:
sum = 1.183333#include<stdio.h>
double f(int n)
{int i;double m=1;for(i=n;i<=2*n-1;i++){m=m*i;}return m;
}
int main()
{int n,i;double sum=0;scanf("%d",&n);for(i=1;i<=n;i++){sum=sum+1.0/f(i);}printf("sum = %.6f",sum);return 0;
}7-4 计算圆柱体的体积
输入圆柱的高和半径,求圆柱体积,volume=π×r2×h 。要求定义和调用函数cylinder (r, h )计算圆柱体的体积。
输入格式:
输入在一行中给出2个实数,分别为半径r和高h。
输出格式:
在一行中以“Volume = 值”的形式输出圆柱体的体积,结果保留三位小数。
输入样例:
3.0 10
输出样例:
Volume = 282.743#include<stdio.h>
#define pl 3.1415926
double cylinder(double r,double h)
{double v;v=pl*r*r*h;return v;
}
int main()
{double r,h;double z;scanf("%lf %lf",&r,&h);z=cylinder(r,h);printf("Volume = %.3f",z);return 0;
}7-5 出生年
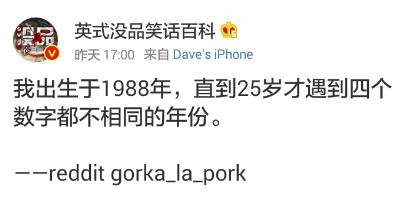
以上是新浪微博中一奇葩贴:“我出生于1988年,直到25岁才遇到4个数字都不相同的年份。”也就是说,直到2013年才达到“4个数字都不相同”的要求。本题请你根据要求,自动填充“我出生于y年,直到x岁才遇到n个数字都不相同的年份”这句话。
输入格式:
输入在一行中给出出生年份y和目标年份中不同数字的个数n,其中y在[1, 3000]之间,n可以是2、或3、或4。注意不足4位的年份要在前面补零,例如公元1年被认为是0001年,有2个不同的数字0和1。
输出格式:
根据输入,输出x和能达到要求的年份。数字间以1个空格分隔,行首尾不得有多余空格。年份要按4位输出。注意:所谓“n个数字都不相同”是指不同的数字正好是n个。如“2013”被视为满足“4位数字都不同”的条件,但不被视为满足2位或3位数字不同的条件。
输入样例1:
1988 4
输出样例1:
25 2013
输入样例2:
1 2
输出样例2:
0 0001# include<stdio.h>
int main()
{int m,n,i,j,k,l,ch[4];scanf("%d %d",&m,&n);for(i=m;i<10000;i++){j=1;l=i;for(k=0;k<4;k++,l/=10)ch[k]=l%10;if(ch[0]!=ch[1]&&ch[0]!=ch[2]&&ch[0]!=ch[3])j++;if(ch[1]!=ch[2]&&ch[1]!=ch[3])j++;if(ch[2]!=ch[3])j++;if(j==n)break;}printf("%d %04d",i-m,i);return 0;
}7-6 sdut-C语言实验-斐波那契数列
编写计算斐波那契(Fibonacci)数列的第n项函数fib(n)(n < 40)。
数列描述:
f1=f2==1;
fn=fn-1+fn-2(n>=3)。
输入格式:
输入整数 n 的值(0 < n < 40)。
输出格式:
输出fib(n)的值。
输入样例:
7
输出样例:
13#include<stdio.h>
int fib(int n)
{if(n==1)return 1;else if(n==2)return 1;elsereturn fib(n-1)+fib(n-2);
}
int main()
{int n;scanf("%d",&n);printf("%d",fib(n));return 0;
}7-7 sdut-C语言实验- 计算题
一个简单的计算,你需要计算f(m,n),其定义如下:
当m=1时,f(m,n)=n;
当n=1时,f(m,n)=m;
当m>1,n>1时,f(m,n)= f(m-1,n)+ f(m,n-1)
输入格式:
第一行包含一个整数T(1<=T<=100),表示下面的数据组数。
以下T行,其中每组数据有两个整数m,n(1<=m,n<=2000),中间用空格隔开。
输出格式:
对每组输入数据,你需要计算出f(m,n),并输出。每个结果占一行。
输入样例:
在这里给出一组输入。例如:
2
1 1
2 3
输出样例:
在这里给出相应的输出。例如:
1
7#include<stdio.h>
int f(int m,int n)
{if(m==1)return n;else if(n==1)return m;elsereturn f(m-1,n)+f(m,n-1);
}
int main()
{int t,m,n,i;scanf("%d",&t);for(i=0;i<t;i++){scanf("%d %d",&m,&n);printf("%d\n",f(m,n));}return 0;
}相关文章:

程序设计基础I-实验7 函数(编程题)
7-1 sdut- C语言实验—计算表达式 计算下列表达式值: 输入格式: 输入x和n的值,其中x为非负实数,n为正整数。 输出格式: 输出f(x,n),保留2位小数。 输入样例: 3 2输出样例: 在这里给出相应的输出。例如: 2.00 …...
使用3080ti配置安装blip2
使用3080ti运行blip2的案例 本机环境(大家主要看GPU,ubuntu版本和cuda版本即可):安装流程我最后安装的所有包的信息(python 3.9 )以供参考(environment.yml): 本机环境&a…...

vue3组件通信之defineEmits
一、defineEmits是什么? defineEmits 是vue3提供的方法,又称为自定义事件,不需要引入可以直接使用,用于子组件与父组件通信。 二、使用样例 1.父组件代码 代码如下(示例): <template>…...

rust gio-rs 挂载 samba 磁盘
linux 使用的 gio 管理工具 这个工具如下 这是 gio 的rust版本 https://crates.io/crates/gio 可以用 rust 语言实现下面所有操作 gio mout 挂载 samba 如下 //https://valadoc.org/gio-2.0/GLib.MountOperation.html pub async fn gio_mount(uri路径:&str, 用户名:Opti…...
)
幸存者游戏(类)
#include <iostream> #include <graphics.h> #include <stdio.h> #include <conio.h> #include <vector> #include <string> using namespace std; int idx_player_anim 0; const int player_anim_num 6;//这里要把动画帧数定位const i…...

SQL 中UPDATE 和 DELETE 语句的深入理解与应用
在 SQL 中,UPDATE和DELETE语句是用于操作表数据的重要工具,它们允许我们对已存在的数据进行修改和删除。 一、UPDATE 语句 (一)基本语法 UPDATE语句的基本语法如下: UPDATE table_name SET column1 value1, colum…...

在 Windows 上查找和结束占用特定端口占用程序,并杀死
在 Windows 上查找和结束占用特定端口(如 9003)的程序,你可以使用以下步骤: 步骤 1:找到占用端口的进程 ID (PID) 打开命令提示符(按 Win R,输入 cmd,然后按回车)。输…...

sql server尽量避免滥用影响性能的标量函数
相信很多新手学了 函数的用法就不可避免的想把学到的东西用起来,然而这个函数使用却有坑, 在实际用的时候我发现一个简单的计算封装 ,不用函数和用函数执行耗时差太多了。 能避免列上进行函数则尽量避免,这是在实际上遇到的坑 &am…...
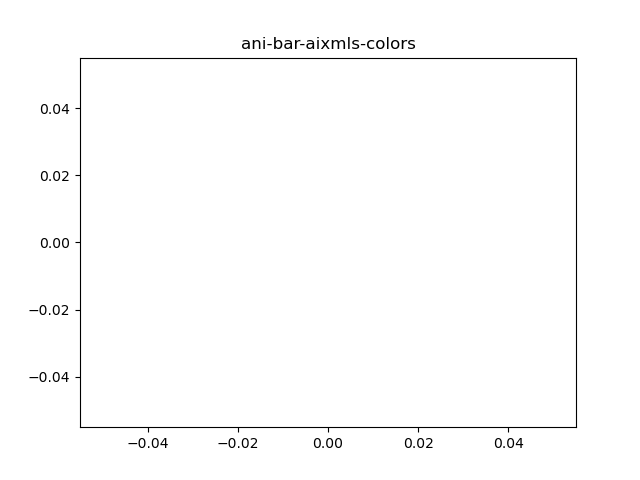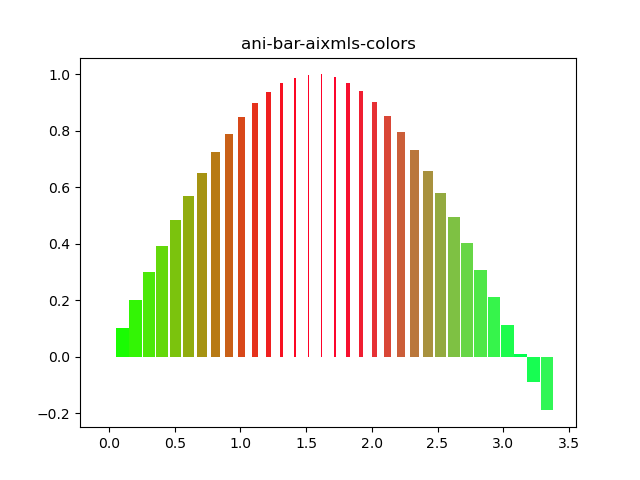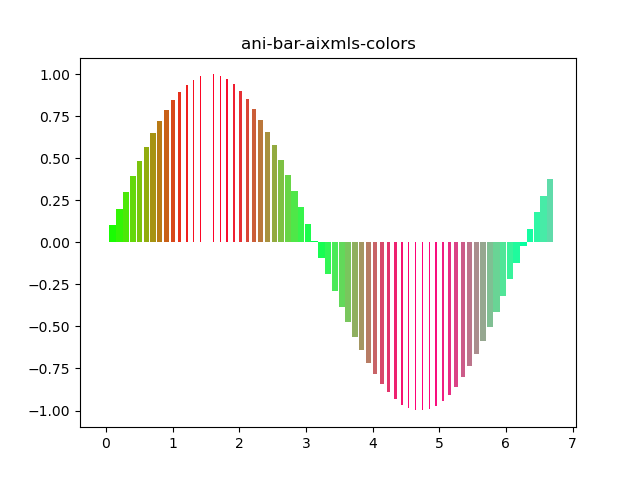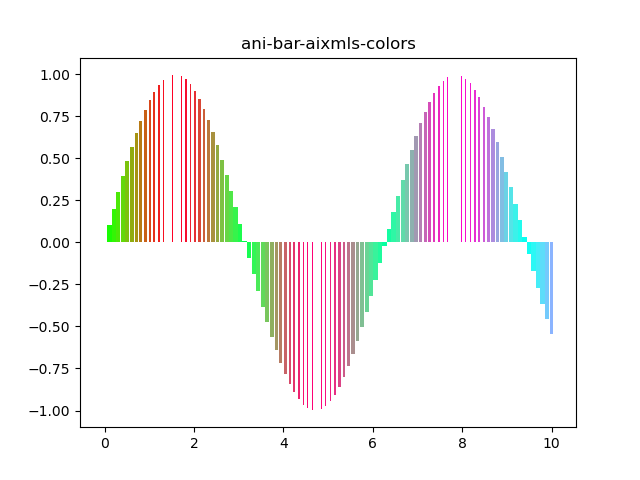
python画图|二维动态柱状图输出
【1】引言 在前面的学习过程中,已经探索过二维柱状图和三维柱状图的绘制教程,包括且不限于的文章链接有: python画图|水平直方图绘制_绘制水平直方图-CSDN博客 python画图|3D bar进阶探索_ax.bar3d-CSDN博客 此外也学习了动态的直线输出和…...

CocosCreator 快速部署 TON 游戏:Web2 游戏如何使用 Ton支付
在本篇文章中,我们将继续探讨如何使用 Cocos Creator 开发 Telegram 游戏,重点介绍如何集成 TON 支付功能。通过这一教程,开发者将学会如何在游戏中接入 TON Connect,实现钱包连接、支付以及支付后的校验流程,最终为 W…...
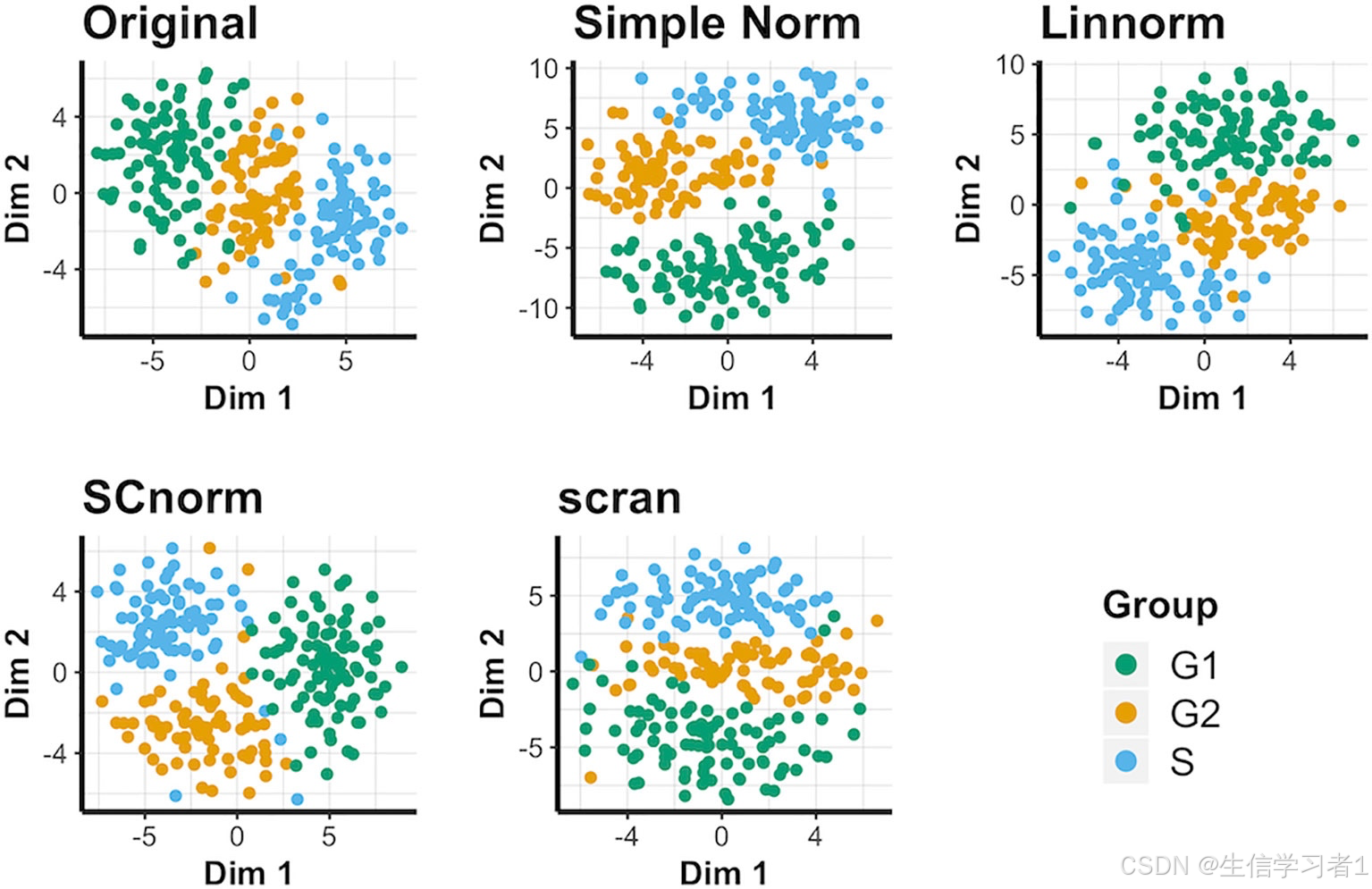
生信初学者教程(二十八):单细胞数据标准化
文章目录 介绍加载R包导入数据消除测序深度影响评估细胞周期的影响识别高度可变的特征缩放数据降维聚类输出结果总结介绍 scRNA-seq的标准化是一个重要的预处理步骤,目的是消除技术变异(比如比如测序深度和基因长度等因素),使基因表达和/或样本之间的比较更加可靠。标准化方…...

【OceanBase诊断调优】—— 错误码 5065 和 5066 的区别
适用版本:V2.1.x、V2.2.x、V3.1.x、V3.2.x 5065 与 5066 是两个近似的报错。 OB_ERR_QUERY_INTERRUPTED(-5065): Message: Query execution was interrupted。 含义为执行中断, 例如终端执行 SQL 过程中按 ctrlc 终止 SQL 执行会报 -5065。 OB_ERR_SESSION_INTER…...

Spring Boot RESTful API开发教程
一、RESTful API简介 RESTful API是一种基于HTTP协议的Web API,其设计原则是简单、可扩展、轻量级、可缓存、可靠、可读性强。RESTful API通常使用HTTP请求方法(GET、POST、PUT、DELETE等)来操作资源,使用HTTP状态码来表示操作结…...

<Rust>iced库(0.13.1)学习之番外:如何为窗口添加初始值?
前言 本专栏是学习Rust的GUI库iced的合集,将介绍iced涉及的各个小部件分别介绍,最后会汇总为一个总的程序。 iced是RustGUI中比较强大的一个,目前处于发展中(即版本可能会改变),本专栏基于版本0.12.1. 注:新版本已更新为0.13 概述 这是本专栏的番外篇,主要介绍一下新…...

Redis:list类型
Redis:list类型 list命令非阻塞LPUSHLRANGELPUSHXRPUSHRPUSHXLPOPRPOPLINDEXLINSERTLLENLREMLTRIMLSET 阻塞BLPOPBRPOP 内部编码ziplistlinkedlistquicklist 几乎每种语言都有顺序表、数组、链表这样的顺序结构,Redis也做出了相应的支持。 如图ÿ…...

政府采购方式有哪些,竞争性谈判和竞争性磋商的区别
政府采购的方式主要包括公开招标、邀请招标、竞争性谈判、竞争性磋商、询价、单一来源采购和框架协议采购等几种。以下是对这些方式的具体介绍: 公开招标 定义:公开招标是指采购单位依法以招标公告的方式邀请不特定的供应商参与投标的采购方式。适用情形…...
)
【JavaScript】移动色块案例 实现一个可以拖动并且在拖动过程中会自动改变颜色的色块(JS 事件监听器)
移动色块案例 实现一个可以拖动并且在拖动过程中会自动改变颜色的色块。 移动色块:用户可以通过鼠标按住并拖动页面上的红色方块(#blocks)。当用户按下鼠标左键时,色块开始跟随鼠标的移动而移动;当用户释放鼠标左键时…...
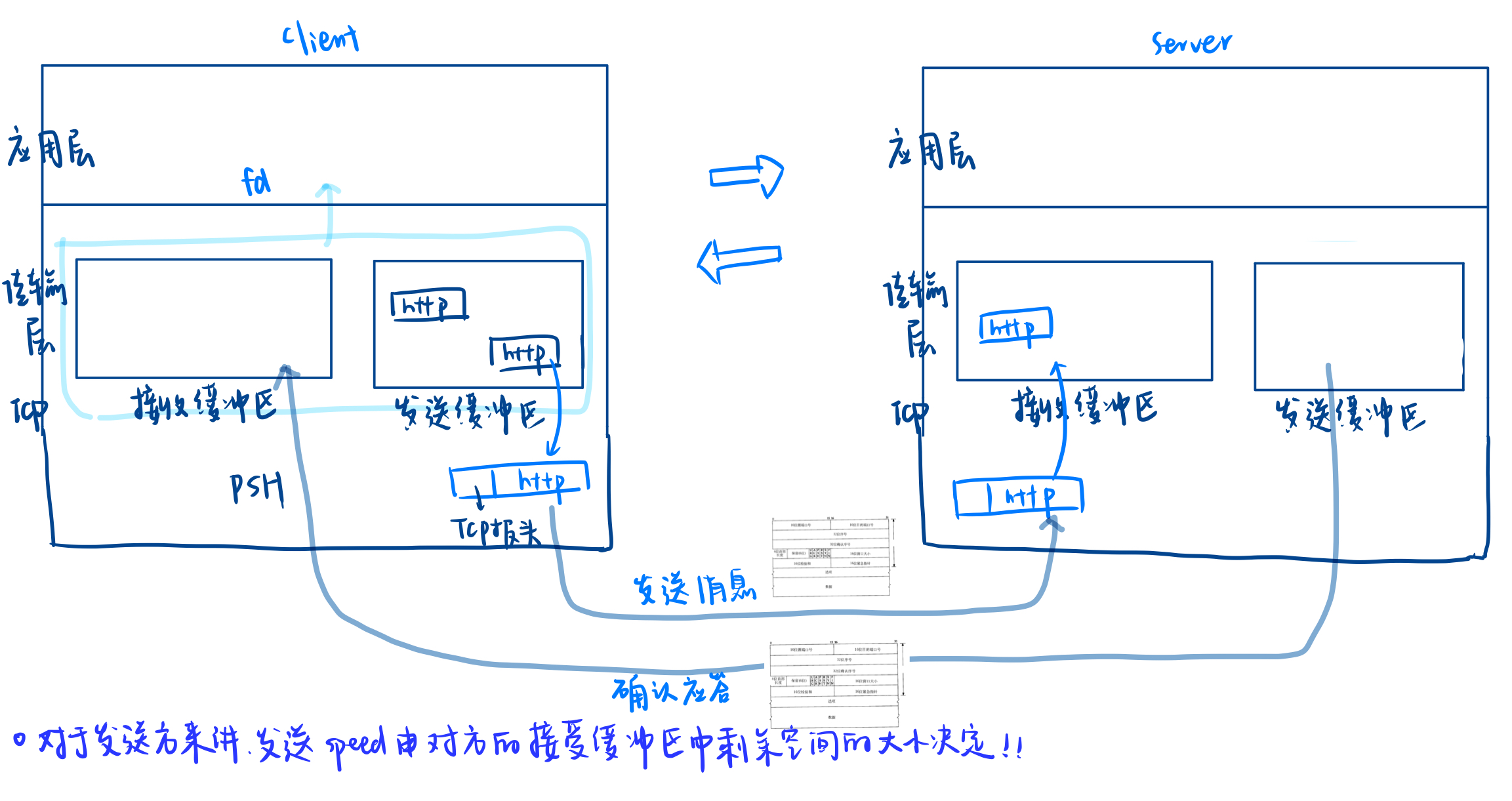
[Linux#62][TCP] 首位长度:封装与分用 | 序号:可靠性原理 | 滑动窗口:流量控制
目录 一. 认识TCP协议的报头 1.TCP头部格式 2. TCP协议的特点 二. TCP如何封装与分用 TCP 报文封装与解包 如何封装解包,如何分用 分离有效载荷 隐含问题:TCP 与 UDP 报头的区别 封装和解包的逆向过程 如何分用 TCP 报文 如何通过端口号找到绑…...

【中短文】区分神经网络中 表征特征、潜层特征、低秩 概念
1. 表征特征(Representational Feature): 表征特征通常指的是输入数据经过NN处理就得到的中间表示或输出表示。 这些特征由NN经学习过程自动提取,能更好捕捉输入数据的本质属性。 例如:在图像识别任务中&…...

MySQL8.0环境部署+Navicat17激活教程
安装MySQL 下载MySQL MySQL官网下载当前最新版本,当前是8.0.39。 选择No thanks, just start my download等待下载即可。 安装MySQL 下载完成后,双击安装进入安装引导页面。选择Custom自定义安装。 选择MySQL Server 8.0.39 - X64安装。 点击Execute执…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...
