Pandas处理时间序列之光谱分析与聚类
import matplotlib.pylab as plt
%matplotlib inline
import numpy as np
from numpy import fft
import pandas as pd一、光谱分析
• 将时间序列分解为许多正弦或余弦函数的总和
• 这些函数的系数应该具有不相关的值
• 对正弦函数进行回归
光谱分析应用场景

基于光谱的拟合
基于光谱的拟合是一种常见的分析方法,它通过将实际观测到的光谱数据与已知的光谱模型进行比较和匹配,来获得对未知样品的估计或预测。该方法可以用于光谱分析、化学定量分析、物质识别等领域

示例

#傅里叶外推算法
def fourierExtrapolation(x, n_predict):n = x.sizen_harm = 5 # 设置了模型中的谐波数量,即傅里叶级数中所包含的谐波数量t = np.arange(0, n)p = np.polyfit(t, x, 1) # 利用线性回归找到了序列 x 中的线性趋势x_notrend = x - p[0] * t # 通过减去线性趋势,将原始数据 x 去趋势化x_freqdom = fft.fft(x_notrend) # 对去趋势化后的数据进行傅里叶变换,将数据从时域转换到频域f = fft.fftfreq(n) # 生成频率数组,用于表示傅里叶变换结果中每个频率对应的频率值indexes = list(range(n))# 对频率数组进行排序,以便从低到高选择频率成分indexes.sort(key = lambda i: np.absolute(f[i]))t = np.arange(0, n + n_predict)restored_sig = np.zeros(t.size)for i in indexes[:1 + n_harm * 2]:ampli = np.absolute(x_freqdom[i]) / n # 振幅phase = np.angle(x_freqdom[i]) # 相位2restored_sig += ampli * np.cos(2 * np.pi * f[i] * t + phase)return restored_sig + p[0] * t# 利用傅立叶变换原理,通过拟合周期函数来预测时间序列的未来值
x = np.array([669, 592, 664, 1005, 699, 401, 646, 472, 598, 681, 1126, 1260, 562, 491, 714, 530, 521, 687, 776, 802, 499, 536, 871, 801, 965, 768, 381, 497, 458, 699, 549, 427, 358, 219, 635, 756, 775, 969, 598, 630, 649, 722, 835, 812, 724, 966, 778, 584, 697, 737, 777, 1059, 1218, 848, 713, 884, 879, 1056, 1273, 1848, 780, 1206, 1404, 1444, 1412, 1493, 1576, 1178, 836, 1087, 1101, 1082, 775, 698, 620, 651, 731, 906, 958, 1039, 1105, 620, 576, 707, 888, 1052, 1072, 1357, 768, 986, 816, 889, 973, 983, 1351, 1266, 1053, 1879, 2085, 2419, 1880, 2045, 2212, 1491, 1378, 1524, 1231, 1577, 2459, 1848, 1506, 1589, 1386, 1111, 1180, 1075, 1595, 1309, 2092, 1846, 2321, 2036, 3587, 1637, 1416, 1432, 1110, 1135, 1233, 1439, 894, 628, 967, 1176, 1069, 1193, 1771, 1199, 888, 1155, 1254, 1403, 1502, 1692, 1187, 1110, 1382, 1808, 2039, 1810, 1819, 1408, 803, 1568, 1227, 1270, 1268, 1535, 873, 1006, 1328, 1733, 1352, 1906, 2029, 1734, 1314, 1810, 1540, 1958, 1420, 1530, 1126, 721, 771, 874, 997, 1186, 1415, 973, 1146, 1147, 1079, 3854, 3407, 2257, 1200, 734, 1051, 1030, 1370, 2422, 1531, 1062, 530, 1030, 1061, 1249, 2080, 2251, 1190, 756, 1161, 1053, 1063, 932, 1604, 1130, 744, 930, 948, 1107, 1161, 1194, 1366, 1155, 785, 602, 903, 1142, 1410, 1256, 742, 985, 1037, 1067, 1196, 1412, 1127, 779, 911, 989, 946, 888, 1349, 1124, 761, 994, 1068, 971, 1157, 1558, 1223, 782, 2790, 1835, 1444, 1098, 1399, 1255, 950, 1110, 1345, 1224, 1092, 1446, 1210, 1122, 1259, 1181, 1035, 1325, 1481, 1278, 769, 911, 876, 877, 950, 1383, 980, 705, 888, 877, 638, 1065, 1142, 1090, 1316, 1270, 1048, 1256, 1009, 1175, 1176, 870, 856, 860])#原始时间序列数据
n_predict = 100 # 未来进行预测的数据点数目
extrapolation = fourierExtrapolation(x, n_predict) # 调用fourierExtrapolation函数,使用原始数据和预测数据点数目作为参数,得到外推的结果
# 使用Matplotlib库绘制了两条曲线,一条代表原始数据x,另一条代表外推的结果extrapolation
plt.plot(np.arange(0, x.size), x, 'b', label = 'x', linewidth = 3)
plt.plot(np.arange(0, extrapolation.size), extrapolation, 'r', label = 'extrapolation')
plt.legend()# 添加图例以便区分曲线
# 通过Fourier外推方法对航空乘客数量的时间序列数据进行预测,并将原始数据和预测结果可视化
air_passengers = pd.read_csv('/home/mw/input/demo2813/AirPassengers.csv') # 读取了包含航空乘客数量的时间序列数据的CSV文件
x = np.array(air_passengers['#Passengers'].values) # 将CSV文件中的乘客数量数据提取出来并转换为Numpy数组,存储在变量x中
n_predict = 300 # 定义外推预测的数据点数目
extrapolation = fourierExtrapolation(x, n_predict) # 调用fourierExtrapolation函数,使用变量x和n_predict作为参数,得到外推的结果
plt.plot(np.arange(0, x.size), x, 'b', label = 'x', linewidth = 3) # 绘制原始数据x的曲线,颜色为蓝色
plt.plot(np.arange(0, extrapolation.size), extrapolation, 'r', label = 'extrapolation') # 绘制外推结果extrapolation的曲线,颜色为红色
plt.legend() # 添加图例,用于区分原始数据和外推结果的曲线
!pip install pandas-datareader -i https://pypi.tuna.tsinghua.edu.cn/simple
!pip install tqdm -i https://pypi.tuna.tsinghua.edu.cn/simple
二、聚类和分类
距离度量
在机器学习和数据挖掘中,分类和聚类是两种常见的任务。虽然它们的目标和方法有所不同,但两者都经常涉及到数据点之间的距离度量。距离度量标准的选择对于分类和聚类的效果至关重要,因为它决定了数据点之间的相似性或差异性的计算方式

应用
基于DTW的聚类
基于DTW的最近邻分类法
import matplotlib.pylab as plt
%matplotlib inline
from matplotlib.pylab import rcParams
rcParams['figure.figsize'] = 15, 6
from pandas_datareader.data import DataReader
from datetime import datetime
from scipy.cluster.hierarchy import dendrogram, linkage
from pandas_datareader.data import DataReader
from datetime import datetime
import pandas as pd
import numpy as np
from sklearn.metrics.pairwise import pairwise_distances
from math import sqrt
from scipy.spatial.distance import squareform
from tqdm import tqdm#读取文件
words = pd.read_csv('/home/mw/input/demo2813/50words_TEST.csv')#从数据框 words 中提取除第一列之外的所有数据,将其转换为矩阵形式,存储在名为 test 的变量中
test = words.ix[:, 1:].as_matrix()'''
/opt/conda/lib/python3.6/site-packages/ipykernel_launcher.py:2: DeprecationWarning:
.ix is deprecated. Please use
.loc for label based indexing or
.iloc for positional indexingSee the documentation here:
http://pandas.pydata.org/pandas-docs/stable/indexing.html#ix-indexer-is-deprecated/opt/conda/lib/python3.6/site-packages/ipykernel_launcher.py:2: FutureWarning: Method .as_matrix will be removed in a future version. Use .values instead.
'''test.shape
# (454, 270)a = lambda x, y: x[0] + y[0]# 计算两个序列之间的动态时间规整(DTW)距离的函数
# DWT是用于衡量两个序列之间相似度的方法,它可以处理序列在时间轴上的扭曲和偏移
def DTWDistance(s1, s2):# 将输入序列转换为NumPy数组s1, s2 = np.array(s1), np.array(s2)n, m = len(s1), len(s2)# 初始化DTW矩阵DTW = np.full((n+1, m+1), float('inf'))DTW[0, 0] = 0# 计算DTW距离for i in range(1, n+1):for j in range(1, m+1):dist = (s1[i-1] - s2[j-1]) ** 2DTW[i, j] = dist + min(DTW[i-1, j], DTW[i, j-1], DTW[i-1, j-1])return np.sqrt(DTW[n, m])# 使用动态时间规整(DTW)距离来计算测试数据集中每对样本之间的距离
# size = test.shape[0]
# distance_matrix = np.zeros((size, size))# for i in tqdm(range(size), desc="计算DTW距离"):
# for j in range(i, size):
# distance_matrix[i, j] = DTWDistance(test[i], test[j])
# distance_matrix[j, i] = distance_matrix[i, j]# 返回distance_matrix的行列数
# distance_matrix.shape# 使用 linkage 函数来对距离矩阵 p 进行层次聚类,聚类方法是 Ward 方法
# z = linkage(distance_matrix, 'ward')# z# np.savetxt('linkage_matrix.txt', z)'''
--------------------------------------------------------------------------------------------------------------------------
注释到这
将下面读取已经在project目录里预存好的数据的代码取消注释
'''from scipy.cluster.hierarchy import dendrogram
# 加载链接矩阵
z = np.loadtxt('linkage_matrix.txt') #读取预存数据
dendrogram(z)
plt.title('层次聚类树状图')
plt.xlabel('样本索引')
plt.ylabel('聚类距离')
plt.show()
#显示前几行数据
words.head()| 4 | -0.89094 | -0.86099 | -0.82438 | -0.78214 | -0.73573 | -0.68691 | -0.63754 | -0.58937 | -0.54342 | ... | -0.86309 | -0.86791 | -0.87271 | -0.87846 | -0.88592 | -0.89619 | -0.90783 | -0.91942 | -0.93018 | -0.93939 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 12 | -0.78346 | -0.68562 | -0.58409 | -0.47946 | -0.37398 | -0.27008 | -0.17225 | -0.087463 | -0.019191 | ... | -0.88318 | -0.89189 | -0.90290 | -0.91427 | -0.92668 | -0.93966 | -0.95244 | -0.96623 | -0.9805 | -0.99178 |
| 1 | 13 | -1.32560 | -1.28430 | -1.21970 | -1.15670 | -1.09980 | -1.04960 | -1.01550 | -0.996720 | -0.985040 | ... | -0.83499 | -0.86204 | -0.88559 | -0.90454 | -0.93353 | -0.99135 | -1.06910 | -1.13680 | -1.1980 | -1.27000 |
| 2 | 23 | -1.09370 | -1.04200 | -0.99840 | -0.95997 | -0.93997 | -0.93764 | -0.92649 | -0.857090 | -0.693320 | ... | -0.72810 | -0.74512 | -0.76376 | -0.78068 | -0.80593 | -0.84350 | -0.89531 | -0.96052 | -1.0509 | -1.12830 |
| 3 | 4 | -0.90138 | -0.85228 | -0.80196 | -0.74932 | -0.69298 | -0.63316 | -0.57038 | -0.506920 | -0.446040 | ... | -0.95452 | -0.97322 | -0.98984 | -1.00520 | -1.01880 | -1.02960 | -1.03700 | -1.04110 | -1.0418 | -1.04030 |
| 4 | 13 | -1.24470 | -1.22000 | -1.16940 | -1.09130 | -0.98968 | -0.86828 | -0.73462 | -0.595370 | -0.457100 | ... | -0.59899 | -0.69078 | -0.78410 | -0.87322 | -0.95100 | -1.01550 | -1.07050 | -1.12200 | -1.1728 | -1.21670 |
# 创建名为 type 的新列,并将数据框 words 中第一列的数据复制到这个新列中
words['type'] = words.ix[:, 1]'''
/opt/conda/lib/python3.6/site-packages/ipykernel_launcher.py:2: DeprecationWarning:
.ix is deprecated. Please use
.loc for label based indexing or
.iloc for positional indexingSee the documentation here:
http://pandas.pydata.org/pandas-docs/stable/indexing.html#ix-indexer-is-deprecated
'''# 筛选出 words 数据框中 type 列的取值小于5的行,并将这些行存储在新的数据框 w 中
w = words[words['type'] < 5]#数据框的行列数
w.shape
# (454, 272)# 绘制数据框 w 中第一行从第二列开始的所有数据的图表
w.ix[0, 1:].plot()
# 绘制数据框 w 中第三行从第二列开始的所有数据的图表
w.ix[2, 1:].plot()
相关文章:

Pandas处理时间序列之光谱分析与聚类
import matplotlib.pylab as plt %matplotlib inline import numpy as np from numpy import fft import pandas as pd 一、光谱分析 • 将时间序列分解为许多正弦或余弦函数的总和 • 这些函数的系数应该具有不相关的值 • 对正弦函数进行回归 光谱分析应用场景 基于光谱的…...

【WebGIS】Cesium:GeoJSON加载
GeoJSON 是一种常用的地理空间数据格式,它用于表示简单的地理要素及其属性,并且被广泛应用于 Web 地图和 GIS 系统中。在 Cesium 中,GeoJSON 文件可以很方便地加载到三维场景中展示,并且可以添加样式和事件处理。本文将为你提供详…...

PageHelper实现分页查询
前端发送的请求参数 后端返回的对象类型 Controller类实现 /*** 员工分页查询* param employeePageQueryDTO* return*/GetMapping("/page")ApiOperation("员工分页查询")public Result<PageResult> page(EmployeePageQueryDTO employeePageQueryDTO)…...
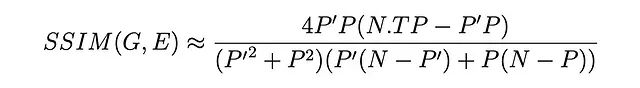
边缘检测评估方法:FOM、RMSE、PSNR和SSIM对比实验和理论研究
图像分割与边缘检测是密切相关的计算机视觉任务。以下图1展示了一个海岸线分割模型的输出示例: 图1: 分割掩码到边缘图的转换过程(数据集:LICS) 模型将每个像素分类为陆地或海洋(分割掩码)。随后,海岸线被定义为分类发生变化的像素位置(边缘图)。边缘检测可以通过提取图像分割…...

MySql 多表查询
多表查询:指从多张表中查询数据。 笛卡儿积:笛卡儿积是指在数学中,两个集合(A集合 和 B集合)的所有组合情况。 连接查询 内连接:相当于查询A、B交集部分数据外连接 左外连接:查询左表所有数据…...

数学建模算法与应用 第11章 偏最小二乘回归及其方法
目录 11.1 偏最小二乘回归概述 11.2 Matlab 偏最小二乘回归命令 Matlab代码示例:偏最小二乘回归 11.3 案例分析:化学反应中的偏最小二乘回归 Matlab代码示例:光谱数据的PLS回归 习题 11 总结 偏最小二乘回归(Partial Least …...

【MATLAB代码】TDOA定位,4个基站、3个时间差、三维定位(可直接复制粘贴到MATLAB上运行)
文章目录 程序结构源代码运行结果代码结构输入输出解析该MATLAB代码实现了基于时间差定位(TDOA, Time Difference of Arrival)的方法,使用最小二乘法在三维空间中估计一个未知点的位置。该算法利用一个主锚点和三个副锚点的已知位置,通过计算信号传播时间差来推算出目标位置…...

uniapp引入ThorUI的方法
1、下载文件 2、复制相应的文件除了pages 3、往项目中复制即可 4、引入即可实现 5、添加easycome自动引入...

面试官:手写一个New
在JavaScript中,new操作符主要用于创建一个对象示例。通过new操作符,可以创建一个新的对象,并将这个对象的原型链只想一个构造函数的原型对象,然后执行构造函数中的代码初始化这个新对象。 常见的new的使用为 new Array() new Set…...

merlion的dashboard打开方法
安装好merlion包后,在anaconda prompt中进行如下图操作: 先进入创建好的虚拟环境:conda activate merlion再执行命令:python -m merlion.dashboard在浏览器中手动打开图中的地址: http://127.0.0.1:8050 打开后的界面…...

自监督学习:引领机器学习的新革命
引言 自监督学习(Self-Supervised Learning)近年来在机器学习领域取得了显著进展,成为人工智能研究的热门话题。不同于传统的监督学习和无监督学习,自监督学习通过利用未标注数据生成标签,从而大幅降低对人工标注数据…...

Web安全常用工具 (持续更新)
前言 本文虽然是讲web相关工具,但在在安全领域,没有人是先精通工具,再上手做事的。鉴于web领域繁杂戎多的知识点(工具是学不完的,哭),如果你在本文的学习过程中遇到没有学过的知识点࿰…...

不踩坑,青龙面板小问题解决方案~
好久没写了,随手记录一下。 1. 新建目录 很多人跟我一样入坑的手机免root青龙面板,一般用的都是2.10.13版本。这个版本比较早,似乎没有新建目录的功能(也可能是我不会用哈哈),以下是对比图: 大家…...

2025秋招倒计时---招联金融
【投递方式】 直接扫下方二维码,或点击内推官网https://wecruit.hotjob.cn/SU61025e262f9d247b98e0a2c2/mc/position/campus,使用内推码 igcefb 投递) 【招聘岗位】 后台开发 前端开发 数据开发 数据运营 算法开发 技术运维 软件测试 产品策…...

基于yolov8、yolov5的果蔬检测系统(含UI界面、数据集、训练好的模型、Python代码)
项目介绍 项目中所用到的算法模型和数据集等信息如下: 算法模型: yolov8、yolov8 SE注意力机制 或 yolov5、yolov5 SE注意力机制 , 直接提供最少两个训练好的模型。模型十分重要,因为有些同学的电脑没有 GPU࿰…...

出海快报 | “三消+短剧”手游横空出世,黄油相机“出圈”日本市场,从Q1看日本手游市场趋势和机会
编者按:TopOn出海快报栏目为互联网出海从业者梳理出海热点,供大家了解行业最新发展态势。 1.“三消短剧”横空出世,融合创新手游表现亮眼 随着竞争的加剧,新产品想要突出重围,只能在游戏中加入额外的元素。第一次打开…...
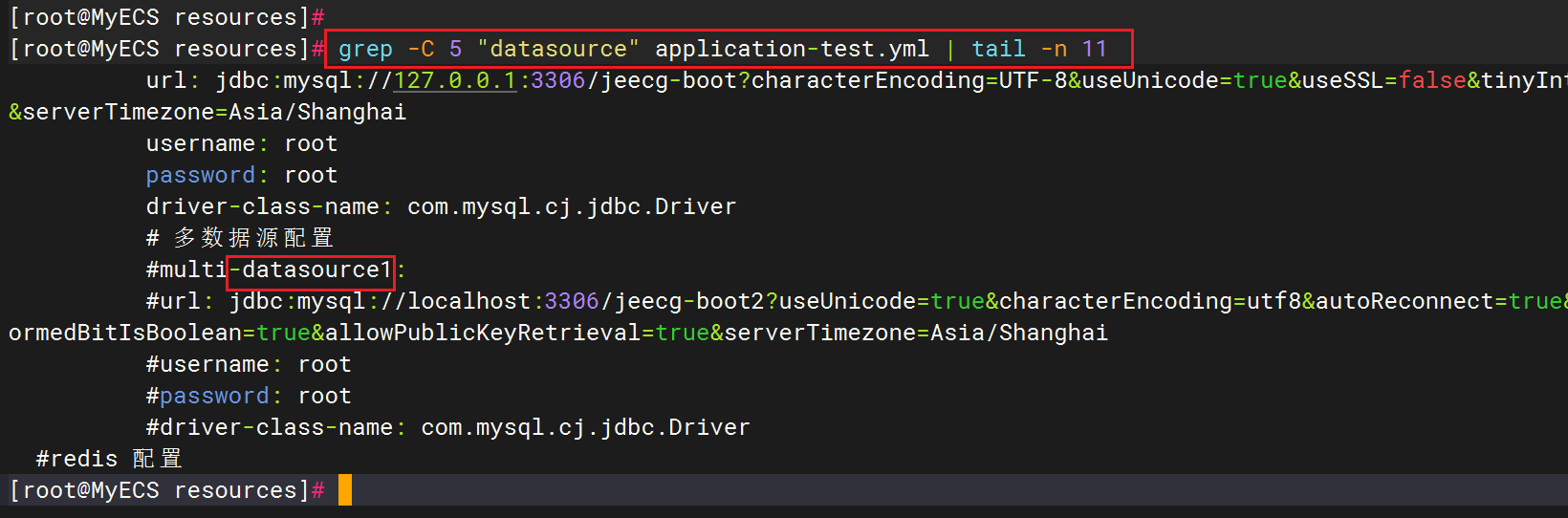
Linux高效查日志命令介绍
说明:之前介绍Linux补充命令时,有介绍使用tail、grep命令查日志; Linux命令补充 今天发现仅凭这两条命令不够,本文扩展介绍一下。 命令一:查看日志开头 head -n 行数 日志路径如下,可以查看程序启动是否…...

非线性关卡设计
【GDC】如何设计完全非线性的单人关卡_DOOM (bilibili.com) 本文章算是此视频的简单笔记,更详细还请看视频 设计完全非线性关卡强调自由移动和沙盒式玩法,鼓励玩家进行不可预测的移动和空间探索。讲解者分享了设计此类关卡的具体步骤,包括明…...

Qt-链接数据库可视化操作
1. 概述 Qt 能够支持对常见数据库的操作,例如: MySQL、Oracle、SqlServer 等等。 Qt SQL模块中的API分为三层:驱动层、SQL接口层、用户接口层。 驱动层为数据库和SQL接口层之间提供了底层的桥梁。 SQL接口层提供了对数据库的访问࿰…...

萤火php端: 查询数据的时候报错: “message“: “Undefined index: pay_status“,
代码:getGoodsFromHistory <?php // ---------------------------------------------------------------------- // | 萤火商城系统 [ 致力于通过产品和服务,帮助商家高效化开拓市场 ] // -----------------------------------------------------…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

【若依】框架项目部署笔记
参考【SpringBoot】【Vue】项目部署_no main manifest attribute, in springboot-0.0.1-sn-CSDN博客 多一个redis安装 准备工作: 压缩包下载:http://download.redis.io/releases 1. 上传压缩包,并进入压缩包所在目录,解压到目标…...

跨平台商品数据接口的标准化与规范化发展路径:淘宝京东拼多多的最新实践
在电商行业蓬勃发展的当下,多平台运营已成为众多商家的必然选择。然而,不同电商平台在商品数据接口方面存在差异,导致商家在跨平台运营时面临诸多挑战,如数据对接困难、运营效率低下、用户体验不一致等。跨平台商品数据接口的标准…...
