动态规划——多状态动态规划问题
目录
一、打家劫舍
二、打家劫舍 II
三、删除并获得点数
四、粉刷房子
五、买卖股票的最佳时机含冷冻期
六、买卖股票的最佳时机含手续费
七、买卖股票的最佳时机III
八、买卖股票的最佳时机IV
一、打家劫舍
打家劫舍

第一步:确定状态表示
当我们每次偷到第i间房子时,我们存在两种状态,即可以选择偷或者不偷该房子的金额。所以我们需要有两张dp表。
f[ i ] 表示偷到第 i 间房子时,小偷选择偷第 i 间房子的金额时,偷窃到的总金额最大。g[ i ]表示偷到第 i 间房子时,小偷选择不偷第 i 间房子的金额时,偷窃到的总金额最大。

第二步:推出状态转移方程

第三步:初始化dp表
我们在使用状态转移方程时,会用到 i-1位置的值,那么如果 i 为0的话,就会有越界访问的问题,所以我们需要初始化,f[0] = nums[0],g[i] = 0。
填表顺序:因为在填写 i 位置的值时,我们要用到 i-1位置的值,所以需要从左往右依次填写。
最后的返回值:我们要返回光顾完所有房子后,所能偷到的最大金额,所以需要返回f[n-1] 和 g[i-1]两者的最大值。
解题代码:
class Solution
{
public:int rob(vector<int>& nums) {int n = nums.size();vector<int> f(n);vector<int> g(n);f[0] = nums[0];for(int i = 1; i < n; i++){f[i] = g[i-1] + nums[i];g[i] = max(f[i-1], g[i-1]);}return max(f[n-1], g[n-1]);}
}; 
二、打家劫舍 II
打家劫舍II

打家劫舍II和打家劫舍问题唯一不同的是,这道题的房子是围成一个圈的。我们可以将它转换成打家劫舍问题去处理。

其他方法就和打家劫舍问题一样了。
返回值就是上面两种情况的最大值。
解题代码:
class Solution
{
public:int rob(vector<int>& nums) {int n = nums.size();return max(nums[0] + rob1(nums, 2, n-2), rob1(nums, 1, n-1));}int rob1(vector<int>& nums, int left, int right){int n = nums.size();if(left > right)return 0;vector<int> f(n);vector<int> g(n);f[left] = nums[left]; // 区间的起始位置是leftfor(int i = left; i <= right; i++){f[i] = g[i-1] + nums[i];g[i] = max(g[i-1], f[i-1]);}return max(g[right], f[right]); // 区间的最右是right}
};
三、删除并获得点数
删除并获得点数

预处理:我们需要注意题目说明中的这一句:选择任意一个 nums[i] ,删除它并获得 nums[i] 的点数。之后,你必须删除所有等于 nums[i] - 1 和 nums[i] + 1 的元素。
也就是说,你在拿到nums[i]的点数后,就不能选择它前一个和后一个元素了。比如,nums[i]为5,拿到5这个点数后,你就不能再拿3和4了。这个要求是不是又和打家劫舍很像了。所以我们最终还是将这个问题转换成了打家劫舍问题。
比如对于示例2:

解题代码:
class Solution
{
public:int deleteAndEarn(vector<int>& nums) {int arr[10001] = {0};for(auto x : nums)arr[x] += x;vector<int> f(10001);vector<int> g(10001);f[0] = arr[0];for(int i = 1; i < 10001; i++){f[i] = g[i-1] + arr[i];g[i] = max(g[i-1], f[i-1]);}return max(g[10000], f[10000]);}
};
四、粉刷房子
粉刷房子

第一步:确定状态表示
红:0,蓝:1,绿:2。
dp[i][j]:表示刷到第i个房子时,将其涂成第j种颜色时的最小花费。
第二步:推出状态转移方程

第三步:初始化dp表
在使用dp表时,要使用i-1,所以 i == 0时,就会发生越界访问的问题。所以初始化,
dp[0][0] = costs[0][0],dp[0][1] = costs[0][1],dp[0][2] = costs[0][2]。
填表顺序:从上向下,从左到右
最后的返回值是最后一行的最大值。
解题代码:
class Solution
{
public:int minCost(vector<vector<int>>& costs) {int m = costs.size(), n = costs[0].size();// 红:0,蓝:1,绿:2// dp[i][j]:表示刷到第i个房子时,将其涂成第j种颜色时的最小花费vector<vector<int>> dp(m, vector<int>(3));dp[0][0] = costs[0][0], dp[0][1] = costs[0][1], dp[0][2] = costs[0][2];for(int i = 1; i < m; i++){dp[i][0] = min(dp[i-1][1], dp[i-1][2]) + costs[i][0];dp[i][1] = min(dp[i-1][0], dp[i-1][2]) + costs[i][1];dp[i][2] = min(dp[i-1][0], dp[i-1][1]) + costs[i][2];}return min(dp[m-1][0], min(dp[m-1][1], dp[m-1][2]));}
};
五、买卖股票的最佳时机含冷冻期
买卖股票的最佳时机含冷冻期

第一步:确定状态表示
根据题意和示例,大的状态表示就是在第i天结束后,所获得的最大利润,而对于第i天来说,我们又有三种可能的状态:卖出,买入,冷冻期。
卖出状态:0,买入状态:1,冷冻期:2
所以说,dp[i][j]:表示第 i 天结束后,处于第 j 种状态时,所获的最大利润。
dp[i][0] 表示: 第 i 天结束之后,处于卖出状态,此时的最大利润。
dp[i][1] 表示: 第 i 天结束之后,处于买入状态,此时的最大利润。
dp[i][2] 表示: 第 i 天结束之后,处于冷冻期状态,此时的最大利润。
第二步:推出状态转移方程

对于上面的核心图,我们对卖出状态进行举例解释一下:
如果在第 i 天结束后处于卖出状态,需要看 i - 1 天是什么状态然后怎么做能够满足第 i 天结束处于卖出状态。
如果第 i - 1 天结束处于卖出状态,那第 i 天什么也不干,依旧处于卖出状态。
如果第 i - 1 天结束处于冷冻期,也就是说第 i 天不能进行任何操作,无法购买股票,当第 i 天结束后,就会结束冷冻期,进入卖出状态。
第三步:初始化dp表,dp[0][1] = -prices[0]。
从左往右,从上向下依次填表,最后返回最后一天的三种状态中的最大值。
解题代码:
class Solution
{
public:int maxProfit(vector<int>& prices) {int m = prices.size();vector<vector<int>> dp(m, vector<int>(3));dp[0][1] = -prices[0];// 卖:0,买:1,冷冻:2for(int i = 1; i < m; i++){dp[i][0] = max(dp[i-1][0], dp[i-1][2]);dp[i][1] = max(dp[i-1][1], dp[i-1][0]-prices[i]);dp[i][2] = dp[i-1][1]+prices[i];}return max(max(dp[m-1][0], dp[m-1][1]), dp[m-1][2]);}
}; 
六、买卖股票的最佳时机含手续费
买卖股票的最佳时机含手续费

第一步:确定状态表示
根据题意,每一天都可能存在两种状态,买入状态和卖出状态。
所以,f[i]:表示第 i 天结束后,处于买入状态时,所获的最大利润。g[i]:表示第 i 天结束后,处于卖出状态时,所获的最大利润。
需要注意的是,每次卖出股票,需要支付手续费。
第二步:推出状态转移方程

第三步:初始化dp表,f[0] = -prices[0]。
填表顺序为从左往右依次填写,g[i]和f[i]一起填写。最后的返回值是f[m-1]和f[m-1]中的最大值。
解题代码:
class Solution
{
public:int maxProfit(vector<int>& prices, int fee) {int m =prices.size();vector<int> f(m);vector<int> g(m);f[0] = -prices[0];for(int i = 1; i < m; i++){f[i] = max(f[i-1], g[i-1] - prices[i]);g[i] = max(g[i-1], f[i-1] + prices[i] - fee);}return max(f[m-1], g[m-1]);}
}; 
七、买卖股票的最佳时机III
买卖股票的最佳时机III

第一步:确定状态表示
首先,仍然是 dp[i] 表示第 i 天结束后所获得的最大利润。每一天有两种状态,卖出和买入状态。
而这道题和之前的题目不同的就是,它有交易次数的限制,只能够完成两笔交易。所以对于每一天来说,在卖出和买入状态之下,还有一种状态,那就是一直到第 i 天的交易次数。
所以,dp[i][j] :表示第 i 天结束后,完成了 j 次交易后,所获得的最大利润。0表示完成了0次交易,1表示完成了1次交易,2表示完成了2次交易。
f[i][j] :表示第 i 天结束后,处于买入状态时,完成了 j 次交易后,所获得的最大利润。
g[i][j] :表示第 i 天结束后,处于卖出状态时,完成了 j 次交易后,所获得的最大利润。
第二步:推出状态转移方程

第三步:初始化dp表

填表顺序为从左往右,从上往下依次填写,g[i]和f[i]一起填写。
解题代码:
class Solution
{const int n = -0x3f3f3f3f;
public:int maxProfit(vector<int>& prices) {int m = prices.size();vector<vector<int>> f(m, vector<int>(3, n)); // 买入vector<vector<int>> g(m, vector<int>(3, n)); // 卖出f[0][0] = -prices[0], g[0][0] = 0;for(int i = 1; i < m; i++){for(int j = 0; j < 3; j++){f[i][j] = max(f[i-1][j], g[i-1][j] - prices[i]);g[i][j] = g[i-1][j];if(j-1 >= 0)g[i][j] = max(g[i-1][j], f[i-1][j-1] + prices[i]);}}int ret = 0;for(int i = 0; i < 3; i++){if(g[m-1][i] > ret)ret = g[m-1][i];}return ret;}
}; 
八、买卖股票的最佳时机IV
买卖股票的最佳时机IV

这一道题的思路,和买卖股票的最佳时机III一模一样,只是把最多交易次数限定成了一个未知数。我们所有的解题方法都与他相同。
解题代码:
class Solution
{const int n = -0x3f3f3f3f;
public:int maxProfit(int k, vector<int>& prices) {int m = prices.size();vector<vector<int>> f(m, vector<int>(k+1, n)); // 买入vector<vector<int>> g(m, vector<int>(k+1, n)); // 卖出f[0][0] = -prices[0], g[0][0] = 0;for(int i = 1; i < m; i++){for(int j = 0; j <= k; j++){f[i][j] = max(f[i-1][j], g[i-1][j] - prices[i]);g[i][j] = g[i-1][j];if(j-1 >= 0)g[i][j] = max(g[i-1][j], f[i-1][j-1] + prices[i]);}}int ret = 0;for(int i = 0; i <= k; i++){if(g[m-1][i] > ret)ret = g[m-1][i];}return ret;}
}; 
相关文章:

动态规划——多状态动态规划问题
目录 一、打家劫舍 二、打家劫舍 II 三、删除并获得点数 四、粉刷房子 五、买卖股票的最佳时机含冷冻期 六、买卖股票的最佳时机含手续费 七、买卖股票的最佳时机III 八、买卖股票的最佳时机IV 一、打家劫舍 打家劫舍 第一步:确定状态表示 当我们每次…...

leetcode-10/9【堆相关】
1.数组中的第K个最大元素【215】 思路: 1.1.要使得时间复杂度为O(n),自己实现大顶堆,通过K次调整,顶部元素就是想要的第K个最大元素 1.2.实现大顶堆的过程中,先建堆,建堆是利用递归,本…...

自然语言处理问答系统:技术进展、应用与挑战
自然语言处理问答系统:技术进展、应用与挑战 自然语言处理(NLP)作为人工智能领域的一个重要分支,旨在使计算机能够理解和生成人类语言。问答系统(Q&A System),作为NLP的一个重要应用&#…...

向量数据库!AI 时代的变革者还是泡沫?
向量数据库!AI 时代的变革者还是泡沫? 前言一、向量数据库的基本概念和原理二、向量数据库在AI中的应用场景三、向量数据库的优势和挑战四、向量数据库的发展现状和未来趋势五、向量数据库对AI发展的影响 前言 数据是 AI 的核心,而向量则是数…...

vue中css作用域及深度作用选择器的用法
Vue中有作用域的CSS 当< style>标签有scoped属性时,它的css只作用于当前组建中的元素。vue2和vue3均有此用法; 当使用scoped后,父组件的样式将不会渗透到子组件中。不过一个子组件的根节点会同时受父组件有作用域的css和子组件有作用…...

LLM - 使用 ModelScope SWIFT 测试 Qwen2-VL 的 LoRA 指令微调 教程(2)
欢迎关注我的CSDN:https://spike.blog.csdn.net/ 本文地址:https://spike.blog.csdn.net/article/details/142827217 免责声明:本文来源于个人知识与公开资料,仅用于学术交流,欢迎讨论,不支持转载。 SWIFT …...

2024 年热门前端框架对比及选择指南
在前端开发的世界里,框架的选择对于项目的成功至关重要。不同的框架有着不同的设计理念、生态系统和适用场景,因此,开发者在选框架时需要权衡多个因素。本文将对当前最流行的前端框架——React、Vue、Angular、Svelte 和 Solid——进行详细对…...

map_server
地图格式 此软件包中的工具处理的地图以两个文件的形式存储。YAML 文件描述地图的元数据,并命名图像文件。图像文件编码了占用数据。 图像格式 图像文件描述世界中每个单元格的占用状态,并使用相应像素的颜色表示。在标准配置中,较白的像素…...

无人机航拍视频帧处理与图像拼接算法
无人机航拍视频帧处理与图像拼接算法 1. 视频帧截取与缩放 在图像预处理阶段,算法首先逐帧地从视频中提取出各个帧。 对于每一帧图像,算法会执行缩放操作,以确保所有帧都具有一致的尺寸,便于后续处理。 2. 图像配准 在图像配准阶段,算法采用SIFT(尺度不变特征变换)算…...

搬砖11、Python 文件和异常
文件和异常 实际开发中常常会遇到对数据进行持久化操作的场景,而实现数据持久化最直接简单的方式就是将数据保存到文件中。说到“文件”这个词,可能需要先科普一下关于文件系统的知识,但是这里我们并不浪费笔墨介绍这个概念,请大…...
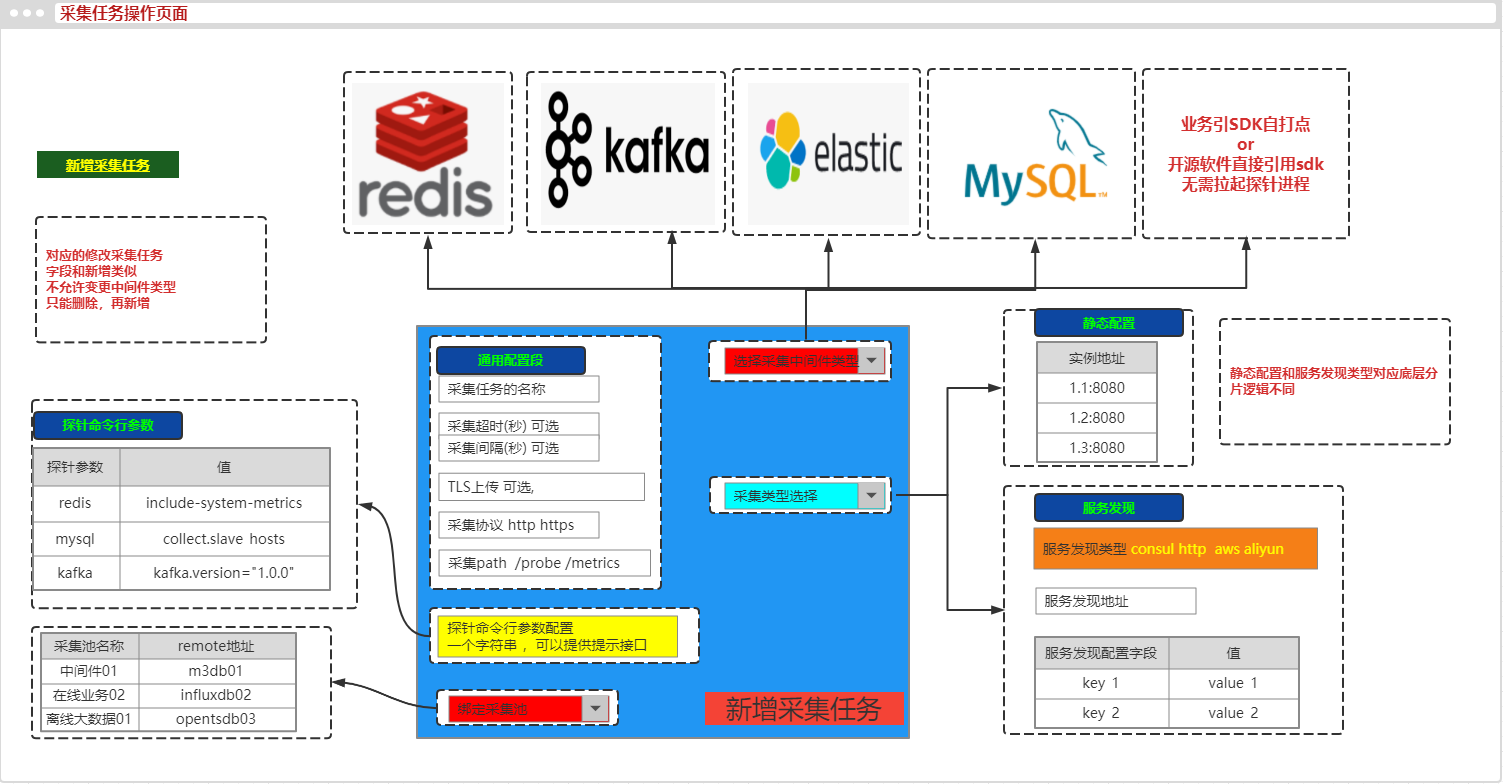
24.6 监控系统在采集侧对接运维平台
本节重点介绍 : 监控系统在采集侧对接运维平台 服务树充当监控系统的上游数据提供者在运维平台上 可以配置采集任务 exporter改造成探针型将给exporter传参和修改prometheus scrape配置等操作页面化 监控系统在采集侧对接运维平台 服务树充当监控系统的上游数据提供者在运…...

refresh-1
如果设置了刷新标志(refreshFlag): - 如果CAT(配置文件管理代理)未初始化,eUICC应返回一个错误代码commandError。 - 对于MEP-A2,eUICC可以返回一个错误代码commandError。 - 如果目标端口上正…...
如何写好一篇计算机应用的论文?
计算机应用是一个广泛的领域,涵盖了从软件开发到数据分析、人工智能、网络安全等多个方向。选择一个合适的毕业设计题目,不仅要考虑个人兴趣和专业技能,还要考虑项目的可行性、创新性以及对未来职业发展的帮助。以下是一些建议,帮…...

工业 5.0 时代的数字孪生:迈向高效和可持续的智能工厂
数字孪生(物理机器或流程的虚拟代表)正在彻底改变工业物联网和流程监控。这项新兴技术可实现实时模拟,提高效率、可持续性并降低成本。航空航天和汽车等行业已经从这些创新系统中获益匪浅 数字孪生是数字模拟器的演变,因此&#x…...

Python脚本之获取Splunk数据发送到第三方UDP端口
原文地址:https://www.program-park.top/2024/10/12/python_21/ 在 Linux 环境执行脚本,Python需要引入对应依赖: pip install splunk-sdk离线环境下,可手动执行python进入 Python 解释器的交互式界面,输入以下命令&a…...

Protobuf:复杂类型接口
Protobuf:复杂类型接口 package字段规则复杂类型enumAnyoneofmap 本博客基于proto3语法,讲解protobuf中的复杂类型。 package 在.proto文件中,支持导入其它.proto文件的内容,例如: test.proto: syntax …...

Git Push 深度解析:命令的区别与实践
目录 命令一:git push origin <branch-name>命令二:git push Factory_sound_detection_tool test工作流程:两者的主要区别实践中的应用总结 Git 是一种分布式版本控制系统,它允许用户对代码进行版本管理。在 Git 中…...
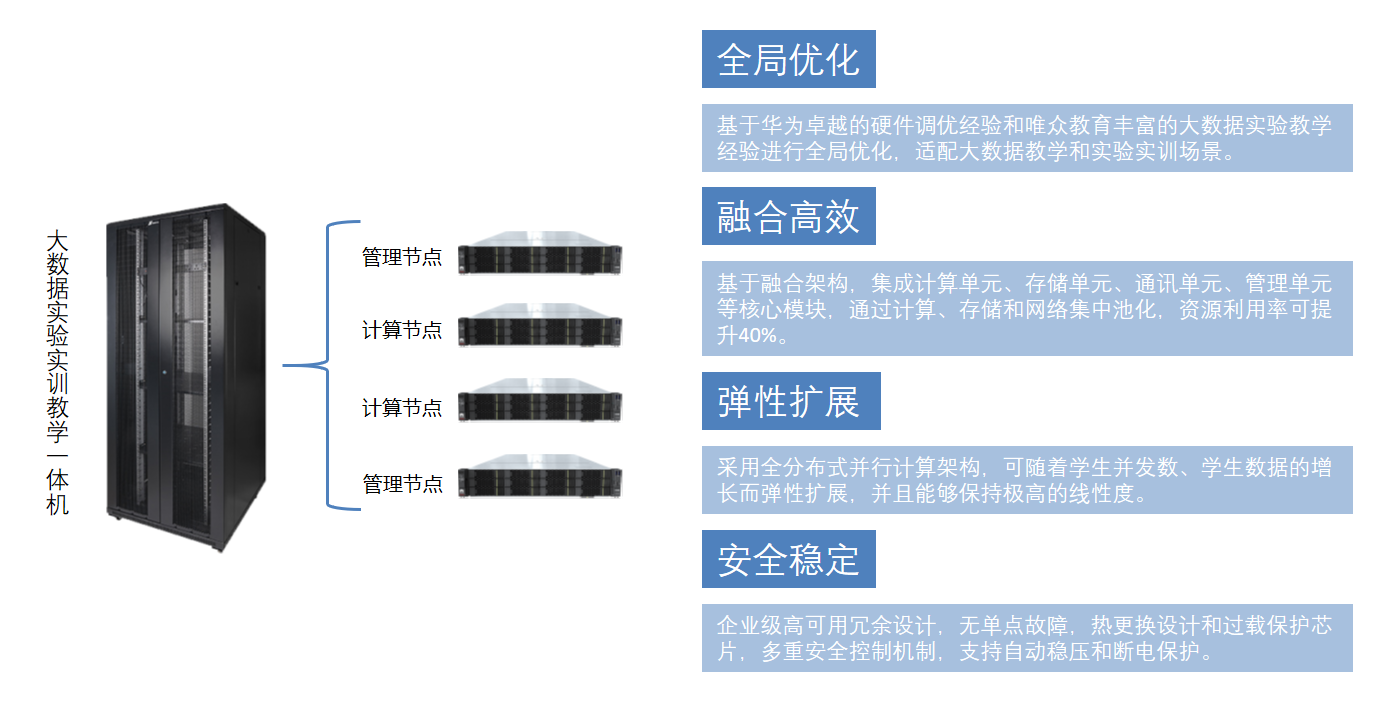
大数据开发基础实训室设备
大数据实验实训一体机 大数据实验教学一体机是一种专为大数据教育设计的软硬件融合产品,其基于华为机架服务器进行了调优设计,从而提供了卓越的性能和稳定性。这一产品将企业级虚拟化管理系统与实验实训教学信息化平台内置于一体,通过软硬件…...
)
【数据结构】string(C++模拟实现)
string构造 string::string(const char* str):_size(strlen(str)) {_str new char[_size 1];_capacity _size;strcpy(_str, str); }// s2(s1) string::string(const string& s) {_str new char[s._capacity 1];strcpy(_str, s._str);_size s._size;_capacity s._cap…...

【笔记】I/O总结王道强化视频笔记
文章目录 从中断控制器的角度来理解整个中断处理的过程复习 处理器的中断处理机制**中断驱动I/O方式** printf——从系统调用到I/O控制方式的具体实现1轮询方式下输出一个字符串(程序查询)中断驱动方式下输出一个字符串中断服务程序中断服务程序与设备驱动程序之间的关系 DMA方…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...
