【Java数据结构】二叉树
【本节目标】
一. 树型结构
1 概念★
- 有一个特殊的结点,称为根结点,根结点没有前驱结点
- 除根结点外,其余结点被分成M(M > 0)个互不相交的集合T1、T2、......、Tm,其中每一个集合Ti (1 <= i <=m) 又是一棵与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继
- 树是递归定义的

注意:树形结构中,子树之间不能有交集,否则就不是树形结构

2 概念★★★

- 结点的度:一个结点含有子树的个数称为该结点的度; 如上图:A的度为6
- 树的度:一棵树中,所有结点度的最大值称为树的度; 如上图:树的度为6
- 叶子结点或终端结点:度为0的结点称为叶结点; 如上图:B、C、H、I...等节点为叶结点
- 双亲结点或父结点:若一个结点含有子结点,则这个结点称为其子结点的父结点; 如上图:A是B的父结点
- 孩子结点或子结点:一个结点含有的子树的根结点称为该结点的子结点; 如上图:B是A的孩子结点
- 根结点:一棵树中,没有双亲结点的结点;如上图:A
- 结点的层次:从根开始定义起,根为第1层,根的子结点为第2层,以此类推
- 树的高度或深度:树中结点的最大层次; 如上图:树的高度为4
树的以下概念只需了解,在看书时只要知道是什么意思即可:
- 非终端结点或分支结点:度不为0的结点; 如上图:D、E、F、G...等节点为分支结点
- 兄弟结点:具有相同父结点的结点互称为兄弟结点; 如上图:B、C是兄弟结点
- 堂兄弟结点:双亲在同一层的结点互为堂兄弟;如上图:H、I互为兄弟结点
- 结点的祖先:从根到该结点所经分支上的所有结点;如上图:A是所有结点的祖先
- 子孙:以某结点为根的子树中任一结点都称为该结点的子孙。如上图:所有结点都是A的子孙
- 森林:由m(m>=0)棵互不相交的树组成的集合称为森林
3 树的表示形式★
class Node {
int value ; // 树中存储的数据Node firstChild ; // 第一个孩子引用Node nextBrother ; // 下一个兄弟引用}

4 树的应用

二. 二叉树★★★
1 概念



2 两种特殊的二叉树

3 二叉树的性质
一棵N个节点的树可以产生N-1条边n0:产生不了边n1:产生n1条边n2:产生2*n2条边n1+2*n2=N-1 ----对于边n0+n1+n2=N- ---对于点联合方程则 n0=n2+1
- 若i>0,双亲序号:(i-1)/2;i=0,i为根结点编号,无双亲结点
- 若2i+1<n,左孩子序号:2i+1,否则无左孩子
- 若2i+2<n,右孩子序号:2i+2,否则无右孩子
1. 某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为( )A 不存在这样的二叉树B 200C 198D 1992. 在具有 2n 个结点的完全二叉树中,叶子结点个数为( )A nB n+1C n-1D n/23. 一个具有 767 个节点的完全二叉树,其叶子节点个数为()A 383B 384C 385D 3864. 一棵完全二叉树的节点数为 531 个,那么这棵树的高度为( )A 11B 10C 8D 12
答案:1.B, n0=n2+1=199-1=1982.A,结点数为偶数个,则度为1的结点为1,结点数为奇数个,则度为1的结点为0,度为2的为x-1个,度为0的为x。本题为x+x-1+1=2n,x=n3.B4.B
4 二叉树的存储
static class TreeNode{public char val;public TreeNode left;public TreeNode right;public TreeNode(char val) {this.val = val;}}孩子双亲表示法后序在平衡树位置介绍,本文采用孩子表示法来构建二叉树。
5 二叉树的基本操作
(1) 前置说明
(2)二叉树的遍历
a. 前中后序遍历

- NLR:前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点--->根的左子树--->根的右子树。
- LNR:中序遍历(Inorder Traversal)——根的左子树--->根节点--->根的右子树。
- LRN:后序遍历(Postorder Traversal)——根的左子树--->根的右子树--->根节点。
// 前序遍历
void preOrder ( Node root );// 中序遍历void inOrder ( Node root );// 后序遍历void postOrder ( Node root );
void preOrder(TreeNode root) {if(root==null){return;}else {char ch = root.val;System.out.print(ch+" ");preOrder(root.left);preOrder(root.right);}}// 中序遍历void inOrder(TreeNode root) {if(root==null){return;}else {char ch = root.val;preOrder(root.left);System.out.print(ch+" ");preOrder(root.right);}}// 后序遍历void postOrder(TreeNode root) {if(root==null){return;}else {char ch = root.val;preOrder(root.left);preOrder(root.right);System.out.print(ch+" ");}}
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {List<Integer> list=new LinkedList<>();public List<Integer> preorderTraversal(TreeNode root) {List<Integer> list=new LinkedList<>();if(root==null){return list;}else{list.add(root.val);}List<Integer> list1= preorderTraversal(root.left);list.addAll(list1);List<Integer> list2= preorderTraversal(root.right);list.addAll(list2);return list;}
}以下为前序遍历的图解:

b. 层序遍历

【练习】根据以上二叉树的三种遍历方式,给出以下二叉树的:

1. 某完全二叉树按层次输出(同一层从左到右)的序列为 ABCDEFGH 。该完全二叉树的前序序列为 ( )A: ABDHECFG B: ABCDEFGH C: HDBEAFCG D: HDEBFGCA2. 二叉树的先序遍历和中序遍历如下:先序遍历: EFHIGJK; 中序遍历: HFIEJKG. 则二叉树根结点为 ( )A: E B: F C: G D: H3. 设一课二叉树的中序遍历序列: badce ,后序遍历序列: bdeca ,则二叉树前序遍历序列为 ( )A: adbce B: decab C: debac D: abcde4. 某二叉树的后序遍历序列与中序遍历序列相同,均为 ABCDEF ,则按层次输出 ( 同一层从左到右 ) 的序列为 ()A: FEDCBA B: CBAFED C: DEFCBA D: ABCDEF【参考答案】 1.A 2.A 3.D 4.A
(3) 二叉树的基本操作
// 获取树中节点的个数int size ( Node root );// 获取叶子节点的个数int getLeafNodeCount ( Node root );// 获取第 K 层节点的个数int getKLevelNodeCount ( Node root , int k );// 获取二叉树的高度int getHeight ( Node root );// 检测值为 value 的元素是否存在Node find ( Node root , int val );// 层序遍历void levelOrder ( Node root );// 判断一棵树是不是完全二叉树boolean isCompleteTree ( Node root );
1.节点个数
//只要节点不为空,那么就count++
//只要节点不为空,那么就count++public static int count=0;public void size(TreeNode root) {if(root==null){return ;}else{count++;size(root.left);size(root.right);}}//整棵树有多少个结点=左子树有多少个结点+右子树有多少个结点+1
public int size(TreeNode root) {if(root==null){return 0;}return size(root.left)+size(root.right)+1;
}2.叶子节点的个数
//只要是叶子结点,那么就count++
public static int count=0;public void getLeafNodeCount(TreeNode root){if(root==null){return ;}if(root.left==null&&root.right==null){count++;}getLeafNodeCount(root.left);getLeafNodeCount(root.right);}//整棵树有多少个叶子结点=左子树有多少个叶子结点+右子树有多少个叶子结点
public int getLeafNodeCount(TreeNode root){if(root==null){return 0;}if(root.left==null&&root.right==null){return 1;}return getLeafNodeCount(root.left)+getLeafNodeCount(root.right);}3.第K层节点的个数
public int getKLevelNodeCount(TreeNode root,int k){if(root==null){return 0;}if(k==1){return 1;}return getKLevelNodeCount(root.left,k-1)+getKLevelNodeCount(root.right,k-1);}4.二叉树的高度
- 时间复杂度:O(N)
- 空间复杂度:O(logN)
public int maxDepth(TreeNode root) {if(root==null){return 0;}int leftHeight=maxDepth(root.left);int rightHeight=maxDepth(root.right);return Math.max(leftHeight,rightHeight)+1;// return (leftHeight>rightHeight?leftHeight+1:rightHeight+1);
}5.value的元素是否存在
如果根节点是则返回根节点,不是则向左子树遍历,左子树不是则向右子树遍历,左右子树都不是则返回空
- 时间复杂度:O(N)
- 空间复杂度:O(logN)
public TreeNode find(TreeNode root, int val){if(root==null){return null;}if(root.val==val){return root;}TreeNode leftNode=find(root.left,val);if(leftNode!=null){return leftNode;}TreeNode rightNode=find(root.right,val);if(rightNode!=null){return rightNode;}return null;}6.层序遍历
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public List<List<Integer>> levelOrder(TreeNode root) {List<List<Integer>> list=new ArrayList<>();if(root==null){return list;}TreeNode cur=root;Queue<TreeNode> queue=new LinkedList<>();queue.offer(root);while(!queue.isEmpty()){List<Integer> list2=new ArrayList<>();int size=queue.size();while(size>0){ cur=queue.poll();list2.add(cur.val);if(cur.left!=null){queue.offer(cur.left);}if(cur.right!=null){queue.offer(cur.right);}size--;} list.add(list2) ;}return list; }
}7.完全二叉树判断
利用队列,如果在弹出值为null时,查看当前queue内的值,如果全部是null则是完全二叉树,否则不是完全二叉树
import java.util.*;/** public class TreeNode {* int val = 0;* TreeNode left = null;* TreeNode right = null;* public TreeNode(int val) {* this.val = val;* }* }*/public class Solution {/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可** * @param root TreeNode类 * @return bool布尔型*/public boolean isCompleteTree (TreeNode root) {if(root==null){return true;}Queue<TreeNode> queue=new LinkedList<>();TreeNode cur=root;queue.offer(root);while(!queue.isEmpty()){cur=queue.poll();if(cur!=null){queue.offer(cur.left);queue.offer(cur.right);}else{break;} }int size=queue.size();while(size>0){TreeNode now=queue.poll();if(now!=null){return false;}size--;} return true; }
}三、 二叉树相关oj题
1. 检查两颗树是否相同。
- 1.判断结构是否一样(左右子树要么同为空,要么同不为空)
- 2.左右子树同为null则正确
- 3.判断值是否一样
- 4.判断左子树,右子树是否一样
- 时间复杂度O(min(M,N))
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public boolean isSameTree(TreeNode p, TreeNode q) {//1.判断结构是否一样if((p!=null&&q==null)||(p==null&&q!=null)){return false;}//上述运行后通过的要么同为空,要么同不为空//同为空则正确if(p==null&&q==null){return true;}//2.判断值是否一样if(p.val!=q.val){return false;}//3.判断左子树,右子树是否一样return isSameTree(p.left, q.left)&&isSameTree(p.right, q.right);}
}2. 另一颗树的子树。
- 当前子树和根节点是否一样
- 当前子树和根节点左子树是否一样
- 当前子树和根节点右子树是否一样
- 时间复杂度O(M*N)
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public boolean isSubtree(TreeNode root, TreeNode subRoot) {if(root==null){return false;}if(isSameTree(root, subRoot)){return true;}if(isSubtree(root.left, subRoot)){return true;} if(isSubtree(root.right, subRoot)){ return true;} return false;}public boolean isSameTree(TreeNode p, TreeNode q) {//1.判断结构是否一样if((p!=null&&q==null)||(p==null&&q!=null)){return false;}//上述运行后通过的要么同为空,要么同不为空//同为空则正确if(p==null&&q==null){return true;}//2.判断值是否一样if(p.val!=q.val){return false;}//3.判断左子树,右子树是否一样return isSameTree(p.left, q.left)&&isSameTree(p.right, q.right);}
}3. 翻转二叉树。
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public TreeNode invertTree(TreeNode root) {if(root==null){return null;}TreeNode tmp=root.left;root.left=root.right;root.right=tmp;invertTree(root.left);invertTree(root.right);return root;}
}4. 判断一颗二叉树是否是平衡二叉树。
- 时间复杂度O(N^2)
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public boolean isBalanced(TreeNode root) {if(root==null){return true;}int leftheight=getheight(root.left);int rightheight=getheight(root.right);return Math.abs(leftheight-rightheight)<2&&isBalanced(root.left)&&isBalanced(root.right);/* if(Math.abs(leftheight-rightheight)>=2){return false;}if(isBalanced(root.left)&&isBalanced(root.right)){return true;}return false;*/}public int getheight(TreeNode root){if(root==null){return 0;}int leftheight=getheight(root.left);int rightheight=getheight(root.right);return Math.max(leftheight,rightheight)+1;}
}- 时间复杂度O(N)
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public boolean isBalanced(TreeNode root) {if(root==null){return true;}return getheight(root)>=0;}public int getheight(TreeNode root){if(root==null){return 0;}int leftheight=getheight(root.left);if(leftheight<0){return -1;}int rightheight=getheight(root.right);if(Math.abs(leftheight-rightheight)<=1&&rightheight>=0){return Math.max(leftheight,rightheight)+1;}else{return -1;}}
}5. 对称二叉树。
root的左子树和root的右子树是否对称
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public boolean isSymmetric(TreeNode root) {if(root==null){return true;}return isSymmetricChild(root.left,root.right);}public boolean isSymmetricChild(TreeNode leftTree,TreeNode rightTree){//判断结构一样if((leftTree==null&&rightTree!=null)||(leftTree!=null&&rightTree==null)){return false;}//左右同为空或者左右同不为空if(leftTree==null&&rightTree==null){return true;}if(leftTree.val!=rightTree.val){return false;}return isSymmetricChild(leftTree.left,rightTree.right)&&isSymmetricChild(leftTree.right,rightTree.left);}}6. 二叉搜索树和双向链表

import java.util.*;
/**
public class TreeNode {int val = 0;TreeNode left = null;TreeNode right = null;public TreeNode(int val) {this.val = val;}}
*/
public class Solution {TreeNode prev = null;public TreeNode Convert(TreeNode pRootOfTree) {if(pRootOfTree==null){return null;}ConvertChild(pRootOfTree);TreeNode head=pRootOfTree;while(head.left!=null){head=head.left;}return head;}public void ConvertChild(TreeNode root) {if (root == null) {return;}ConvertChild(root.left);root.left = prev;if (prev != null) {prev.right = root;}prev = root;ConvertChild(root.right);}
}
7.二叉树的构建及遍历。
import java.util.Scanner;// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {static class TreeNode{public char val;public TreeNode left;public TreeNode right;public TreeNode(char ch) {this.val=ch;}
}public static void main(String[] args) {Scanner in = new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseString str=in.nextLine();TreeNode root= createTree(str);Inorder(root);}}public static int i=0;public static TreeNode createTree(String str){TreeNode root=null;if(str.charAt(i)!='#'){root=new TreeNode(str.charAt(i));i++;root.left=createTree(str);root.right=createTree(str);}else{i++;}return root;}public static void Inorder(TreeNode root){if(root==null){return;}Inorder(root.left);System.out.print(root.val+" ");Inorder(root.right);}
}8. 二叉树的分层遍历 。
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public List<List<Integer>> levelOrder(TreeNode root) {List<List<Integer>> list=new ArrayList<>();if(root==null){return list;}TreeNode cur=root;Queue<TreeNode> queue=new LinkedList<>();queue.offer(root);while(!queue.isEmpty()){List<Integer> list2=new ArrayList<>();int size=queue.size();while(size>0){ cur=queue.poll();list2.add(cur.val);if(cur.left!=null){queue.offer(cur.left);}if(cur.right!=null){queue.offer(cur.right);}size--;} list.add(list2) ;}return list; }
}9. 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先 。
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode(int x) { val = x; }* }*/
class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {if(root==null){return null;}if(root==p||root==q){return root;}TreeNode leftnode=lowestCommonAncestor(root.left, p, q);TreeNode rightnode=lowestCommonAncestor(root.right, p, q);if(leftnode==null){return rightnode;}else if(rightnode==null){return leftnode;}else{return root;}}
}利用前面的把二叉树改成双向链表的思路可以把距离父节点远的向父节点靠近
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode(int x) { val = x; }* }*/
class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {if(root==null){return null;}Stack<TreeNode> stackp=new Stack<>();Stack<TreeNode> stackq=new Stack<>();getPath(root,p,stackp);getPath(root,q,stackq);int sizep=stackp.size();int sizeq=stackq.size();int size=0;if(sizep>sizeq){size=sizep-sizeq;while(size!=0){stackp.pop();size--;}}else{size=sizeq-sizep;while(size!=0){stackq.pop();size--;}}while(!stackp.isEmpty()&&!stackq.isEmpty()){if(stackp.peek()!=stackq.peek()){stackp.pop();stackq.pop();}else{return stackp.pop();}}return null;// if(root==null){// return null;// }// if(root==p||root==q){// return root;// }// TreeNode leftnode=lowestCommonAncestor(root.left, p, q);// TreeNode rightnode=lowestCommonAncestor(root.right, p, q);// if(leftnode==null){// return rightnode;// }else if(rightnode==null){// return leftnode;// }else{// return root;// }}public boolean getPath(TreeNode root,TreeNode p,Stack<TreeNode> stack){if(root==null){return false;}stack.push(root);if(root==p){return true;}boolean leftpath=getPath(root.left,p,stack);if(leftpath){return true;}boolean rightpath=getPath(root.right,p,stack);if(rightpath){return true;}stack.pop();return false;}
}10. 根据一棵树的前序遍历与中序遍历构造二叉树。
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public int preIndex;public TreeNode buildTree(int[] preorder, int[] inorder) {return buildTreeChild(preorder, inorder,0,inorder.length-1);}public TreeNode buildTreeChild(int[] preorder,int[] inorder,int inBegin, int inEnd) {//表示没有子树了if(inBegin>inEnd){return null;}TreeNode root=new TreeNode(preorder[preIndex]);//将首元素作为根节点int midindex=findVal(inorder,inBegin,inEnd,preorder[preIndex]);preIndex++;root.left=buildTreeChild(preorder,inorder,inBegin,midindex-1);root.right=buildTreeChild(preorder,inorder, midindex+1,inEnd);return root;}private int findVal(int[] inorder,int inBegin, int inEnd,int val){for(int i=inBegin;i<=inEnd;i++){if(inorder[i]==val){return i;}}return -1;}
}11. 根据一棵树的中序遍历与后序遍历构造二叉树。
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public int postIndex;public TreeNode buildTree(int[] inorder, int[] postorder) {postIndex=postorder.length-1;return buildTreeChild(inorder,postorder,0,inorder.length-1);}public TreeNode buildTreeChild(int[] inorder, int[] postorder,int inBegin,int inEnd) {if(inBegin>inEnd){return null;}TreeNode root=new TreeNode(postorder[postIndex]);int findindex=findVal(inorder,inBegin,inEnd,postorder[postIndex]);postIndex--;root.right=buildTreeChild(inorder,postorder,findindex+1,inEnd); root.left=buildTreeChild(inorder,postorder,inBegin,findindex-1); return root;}private int findVal(int[] inorder,int inBegin,int inEnd,int val){for(int i=inBegin;i<=inEnd;i++){if(inorder[i]==val){return i;} }return -1;}
}
12. 二叉树创建字符串。
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public String tree2str(TreeNode root) {StringBuilder stringBuilder =new StringBuilder();tree2strChild(root,stringBuilder);return stringBuilder.toString();}public void tree2strChild(TreeNode t,StringBuilder stringBuilder) {if(t==null){return;}stringBuilder.append(t.val);if(t.left!=null){stringBuilder.append('(');tree2strChild(t.left,stringBuilder); stringBuilder.append(')');}else{if(t.right==null){return;}else{stringBuilder.append('(');stringBuilder.append(')');}}if(t.right!=null){stringBuilder.append('(');tree2strChild(t.right,stringBuilder); stringBuilder.append(')');}else{return;}}
}13. 二叉树前序非递归遍历实现
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> list=new LinkedList<>();Stack<TreeNode> stack=new Stack<>();TreeNode cur=root;while(cur!=null||!stack.isEmpty()){while(cur!=null){stack.push(cur);list.add(cur.val);cur=cur.left;}TreeNode top=stack.pop();cur=top.right;}return list;}
}14. 二叉树中序非递归遍历实现。
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> list=new LinkedList<>();Stack<TreeNode> stack=new Stack<>();TreeNode cur=root;while(cur!=null||!stack.isEmpty()){while(cur!=null){stack.push(cur);cur=cur.left;}TreeNode top=stack.pop();list.add(top.val);cur=top.right;}return list;}
}15. 二叉树后序非递归遍历实现。
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public List<Integer> postorderTraversal(TreeNode root) {List<Integer> list=new LinkedList<>();Stack<TreeNode> stack=new Stack<>();TreeNode cur=root;while(cur!=null||!stack.isEmpty()){while(cur!=null){stack.push(cur);cur=cur.left;}TreeNode top=stack.peek();if(top.right==null||list.contains(top.right.val)){top=stack.pop();list.add(top.val);}else{cur=top.right;}}return list;}}/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public List<Integer> postorderTraversal(TreeNode root) {List<Integer> list=new LinkedList<>();Stack<TreeNode> stack=new Stack<>();TreeNode cur=root;TreeNode prev=null;while(cur!=null||!stack.isEmpty()){while(cur!=null){stack.push(cur);cur=cur.left;}TreeNode top=stack.peek();if(top.right==null||top.right==prev){list.add(top.val);top=stack.pop();prev=top;}else{cur=top.right;}}return list;}}if(top.right==null||top.right==prev){//防止不停的在右子树和根子树之间不停循环
list.add(top.val);
top=stack.pop();
prev=top;
}else{
cur=top.right;
}
相关文章:

【Java数据结构】二叉树
【本节目标】 1. 掌握树的基本概念 2. 掌握二叉树概念及特性 3. 掌握二叉树的基本操作 4. 完成二叉树相关的面试题练习 一. 树型结构 1 概念★ 树是一种 非线性 的数据结构,它是由 n ( n>0 )个有限结点组成一个具有层次关系的集…...

虎牙Android面试题及参考答案
给个数组,找出数组中第 k 大的数(利用快排思想 / 用小顶堆,他说可以用大顶堆?) 利用快排思想:快速排序的核心思想是分治和分区。在找数组中第 k 大的数时,每次选择一个基准元素,将数组分为两部分,左边部分小于基准元素,右边部分大于基准元素。如果基准元素最终的下标…...

C++:错误代码分析<2>
🌏主页:R6bandito_ 🚀所属专栏:C/C错误代码收集整理 源码 考虑以下代码: void do_some_work() {std::cout << "Do some work" << std::endl; }int main(int argc, const char* argv[]) {std::…...

怎么ping网络ip地址通不通
怎么Ping网络IP地址通不通?要检查网络中的IP地址是否连通,可以使用Ping命令。Ping命令通过发送ICMP(Internet Control Message Protocol,因特网控制消息协议)Echo请求报文并等待回应,来判断目标主机是否可…...

前端新机部署
编辑器:vscode 下载地址 vscode常用插件 显示代码修改历史、作者等信息 GitLens Nodejs版本 Node版本管理工具 Nvm下载地址 nvm常用命令: nvm ls // 查看安装的所有node.js的版本nvm list available //查看可以安装的所有node.js版本nvm install 版本…...

对比 Babel、SWC 和 Oxc:JavaScript 和 TypeScript 工具的未来
随着现代前端开发的快速演变,JavaScript 和 TypeScript 的工具链不断更新,以满足开发者对性能和效率的需求。我们将对比三款流行的工具:Babel、SWC 和 Oxc,重点分析它们的特点、性能、应用场景以及适用性。 1. Babel:…...

MySQL SELECT 查询(三):查询常用函数大全
MySQL SELECT 查询(三):查询常用函数大全 1. 单行函数 单行函数是 SQL 中一类重要的函数,它们可以对单行数据进行处理,并返回单个结果。单行函数可以嵌套使用,并提供灵活的数据处理能力。 1.1 定义 只对单…...

axios 的 get 请求传参数
在使用 Axios 发起 GET 请求时,参数通常是通过 URL 的查询字符串来传递的。Axios 提供了一个简洁的接口来构建这样的请求,并自动将参数附加到 URL 上。 以下是一个使用 Axios 发起 GET 请求并传递参数的示例: const axios require(axios);…...

用C++编写信息管理系统(歌单信息管理)
C语言是面向过程的编程语言,而C是面向对象的编程语言,在书写代码时风格有所不同(也存在很多共性)。 程序说明 本次系统程序使用的是C语言进行编写,主要考虑怎么实现面向对象的问题。 因为本次程序属于小型系统程序&…...
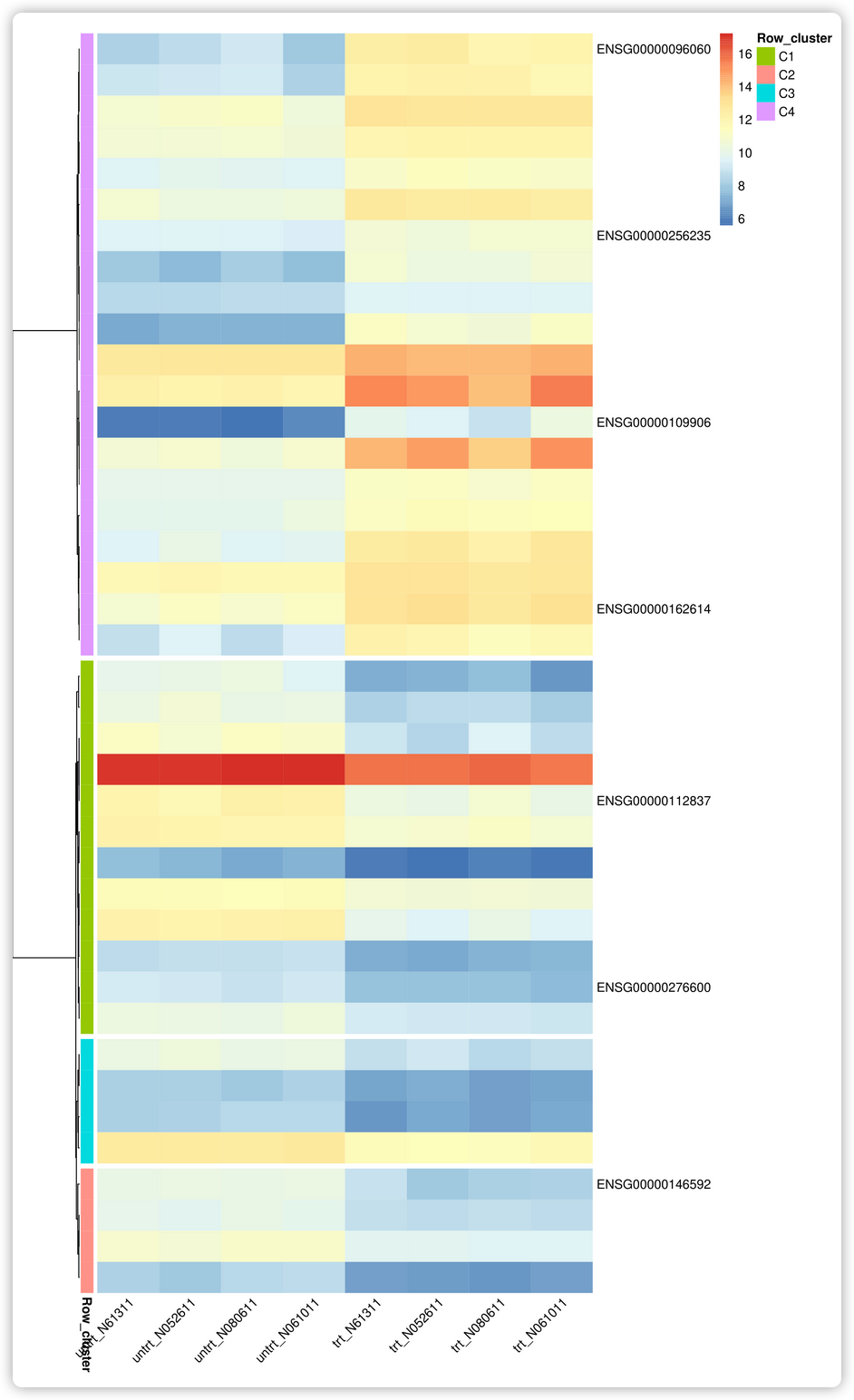
对层级聚类树进行模块分割,定位基因在哪个模块中
拷贝数据到 ImageGP (http://www.ehbio.com/Cloud_Platform/front/#/analysis?pageb%27Ng%3D%3D%27),并设置参数. ID untrt_N61311 untrt_N052611 untrt_N080611 untrt_N061011 trt_N61311 trt_N052611 trt_N080611 trt_N061011 ENSG000…...

机器学习【金融风险与风口评估及其应用】
机器学习【金融风险与风口评估及其应用】 一、机器学习在金融风险评估中的应用1.提升评估准确性2.实现自动化和智能化3.增强风险管理能力4.信用评估5.风险模型6.交易策略7.欺诈检测 二、机器学习在金融风口评估中的应用1.识别市场趋势2.评估创新潜力3.优化投资策略4. 自然语言处…...

【计算机网络 - 基础问题】每日 3 题(三十八)
✍个人博客:https://blog.csdn.net/Newin2020?typeblog 📣专栏地址:http://t.csdnimg.cn/fYaBd 📚专栏简介:在这个专栏中,我将会分享 C 面试中常见的面试题给大家~ ❤️如果有收获的话,欢迎点赞…...
)
深入浅出MongoDB(五)
深入浅出MongoDB(五) 文章目录 深入浅出MongoDB(五)可重试读取可重试写入读关注readConcern支持写关注 可重试读取 可重试读取允许mongodb驱动程序在遇到某些网络或服务器错误时,自动重试某些读取操作一次。只有连接到…...

【conda】创建、激活、删除虚拟环境
前言一、创建虚拟环境二、删除虚拟环境总结 前言 主要是记录一下步骤 一、创建虚拟环境 地址栏输入cmd,唤起命令符栏目,就可以在指定目录下创建虚拟环境了。 这样方便日后在pycharm直接配置虚拟环境。 conda create -n yolo5-lite python3.9 -y简单来说…...

关于int*的*号归属权问题
再根据函数指针定义:int (*int) (int a)。我们发现*和后面的标识符才是一体的 所以int *a,b;的写法更好,说明a是指针类型,b是int类型...

leetcode---素数,最小质因子,最大公约数
1 判断一个数是不是质数(素数) 方法1:依次判断能否被n整除即可,能够整除则不是质数,否则是质数 方法2:假如n是合数,必然存在非1的两个约数p1和p2,其中p1<sqrt(n),p2>sqrt(n)。 方法3&…...

基于stm32的蓝牙模块实验
蓝牙模块定长或不定长发送 头文件 #include "stdio.h" #include "sys.h"#define UART2_RX_BUF_SIZE 128 #define UART2_TX_BUF_SIZE 64UART_HandleTypeDef uart2_handle;uint8_t uart2_rx_buf[UART2_RX_BUF_SIZE]; uint16_t uart2_rx_len 0; void b…...

C语言解决TopK问题
前言: 本文TopK问题是在数据量很大的前提下进行解决,当数据量足够大时,内存中存不下,只能存到文件硬盘中。当存到硬盘中,我们无法用建堆,一个一个pop取出最值的方式解决,因为我们没法在硬盘中去…...
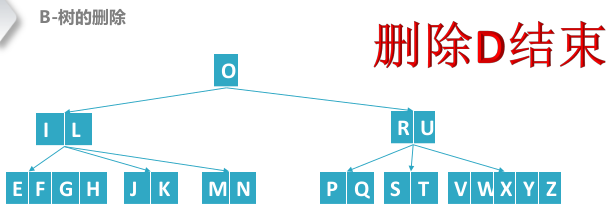
磁盘存储链式结构——B树与B+树
红黑树处理数据都是在内存中,考虑的都是内存中的运算时间复杂度。如果我们要操作的数据集非常大,大到内存已经没办法处理了该怎么办呢? 试想一下,为了要在一个拥有几十万个文件的磁盘中查找一个文本文件,设计的…...
如何批量从sql语句中提取表名
简介 使用的卢易表 的提取表名功能,可以从sql语句中批量提取表名。采用纯文本sql语法分析,无需连接数据库,支持从含非sql语句的文件文件中提取,支持各类数据库sql语法。 特点 快:从成百个文件中提取上千个表名只需1…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...
