C++进阶——二叉搜索树
目录
一、基本概念
二、性能分析
三、模拟实现
四、使用场景
1.key搜索场景
2.key/value搜索场景
一、基本概念
二叉搜索树(Binary Search Tree),看名字就知道,是可以用来搜索数据的一种二叉树。
它可以是空树(一个数据都没有的二叉搜索树),也可以只有一个根结点,这都是比较特殊的情况。但其实二叉搜索树都是从一个根节点开始构建的,然后一个结点一个结点的插入,就会形成一个比较大型的二叉搜索树。
像这样:

仔细观察就可以发现,对于每一个结点,它的左孩子结点数据比它小,右孩子结点数据比它大。
其实,对于每一个结点,它的左子树所有结点的数据都会比它小,右子树所有结点的数据都会比它大,它的左子树和右子树又分别也是一颗二叉搜索树。
另外,看一下它的中序遍历序列:[1,3,4,6,7,8,10,13,14],可以发现是升序的,这是因为:二叉搜索树的最小单元(一父+二子)的中序遍历是升序的,那么递归下来,自然整个二叉搜索树的中序遍历序列也是升序的了。
肯定有人会疑惑,左子树的结点数据也可能比根结点的数据大吧?!
这是不会的,因为在二叉搜索树构建的过程中,结点的插入是靠循环,如果比当前结点数据大,就往右走,小,就往左走。就像上面的图中,根结点的左子树中最大数字位7,如果是9,那么9必然会在插入的时候就插入到根结点的右子树上。
二叉搜索树可以实现出两个版本:支持插入相同数据/不支持插入相同数据,两者要看应用场景来看具体使用哪一种情况。
到后面,我们会学习map/set、multimap/multiset,它们的底层就是二叉搜索树,前一组不支持插入相等值,二后一组支持。
二、性能分析
二叉搜索树,听名字就知道是为查找而生。
以我们之前学习的经验,查找效率取决于该二叉搜素树的高度。(最坏情况下要进行最大高度次查找)
如果该二叉搜索树是满二叉树,那么就是比较理想的情况,查找效率为O(logN);
但是如果极端情况下,像下图这样,查找效率就会变成O(N)。

想要解决这种情况当然是有办法的,也就是建立平衡二叉搜索树,不过这个知识不是本博客的重点,到后面的博客会详细说。
三、模拟实现
先说明,我们的模拟实现对于增删查改只实现了增删查,不实现改的操作,很好理解,如果把二叉搜索树某个结点的数据修改了,那么这个二叉搜索树的结构也就可能被破坏掉了,在后续需要进行的搜索操作中很容易出现错误。
如果你非得想实现改,建议直接删除+插入。
先搭建出整体框架:
// BinarySearch.h
#pragma once
#include <iostream>
using namespace std;// K : key
template<class K>
struct BSTNode
{K _key;BSTNode<K>* _left;BSTNode<K>* _right;BSTNode(K key):_key(key),_left(nullptr),_right(nullptr){}
};template<class K>
class BSTree
{using Node = BSTNode<K>;public:private:Node* _root;
};下面这里是中序遍历以及增查(删除后面重点说):
// BinarySearch.h
#pragma once
#include <iostream>
using namespace std;// K : key
template<class K>
struct BSTNode
{K _key;BSTNode<K>* _left;BSTNode<K>* _right;BSTNode(K key):_key(key),_left(nullptr),_right(nullptr){}
};template<class K>
class BSTree
{using Node = BSTNode<K>;
public:// 查找bool Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key) cur = cur->_right;else if (cur->_key > key) cur = cur->_left;else return true;}return false;}// 插入bool Insert(const K& key){if (_root == nullptr){_root = new Node(key);return true;}// Node* newnode = new Node(key);// 在下面直接让cur变成新结点,就省去这一步了// 注意 *parentNode* cur = _root, *parent = _root;// 我们要实现的是不支持插入重复数据的元素的搜索二叉树,所以需要先查找while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else return false;}cur = new Node(key);if (parent->_key > key) parent->_left = cur;else parent->_right = cur;return true;}// 删除bool Erase(const K& key){}// 中序遍历void InOrder(){_InOrder(_root);cout << endl;}private:void _InOrder(Node* root){// 空指针不能->,判一下空if (root == nullptr) return;_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}private:Node* _root = nullptr;
};// Test.cpp
#include "BinarySearch.h"int main()
{BSTree<int> bst;int a[] = { 8, 3, 1, 10, 1, 6, 4, 7, 14, 13 };for (auto e : a){bst.Insert(e);}bst.InOrder();return 0;
}二叉搜索树的删除:
二叉搜索树的删除,所需要删除的结点类型有种:
1.叶子结点:直接删就行,父结点对应位置置空
2.只有一个孩子的父结点:把唯一一个孩子给该父结点的父结点,再删除该结点即可
3.有两个孩子的父结点:这就有点麻烦了......
之前学过堆,有可能能想出这种方法:
让需要删除的结点和某个结点交换数据,然后删除该结点,再把交换上来的结点向下调整,这种方法看起来确实可行,那么就不妨一试。
选择的结点为哪个?为了保证删除效率我们尽量减少交换后向下调整的次数,所以尽量就是让它不需要向下调整即可。那么我们就可以达到:交换+删除结点(搜索二叉树结构不被破坏),即可成功删除指定结点。

结合这张图,我们要删除3,关于交换结点的选取,我们可以这样想:
1. 3的父结点是8,以3为根结点的搜索二叉树(后面叫3树)的值都是小于8的,所以无论交换3树上面的哪个结点,都不会影响交换上来的结点与8的关系。
2. 3树中3把左右子树分成了小于和大于3的两部分值,如果我们把3删去,那么充当分界值的数字只能是紧挨3的数字,在这里是1或4(3树的中序遍历:13467,紧挨3的是1和4),所以用1或4与3交换都可以(不会破坏二叉搜索树的结构)。
3.紧接着2,我们仔细观察搜索二叉树不难发现,1是3左子树的最大数据,4是3右子树的最小数据,也就是说,我们可以使要删除的结点与它左子树的最大数据结点或者右子树的最小数据结点交换,然后再删除交换到左子树最大/右子树最小结点的待删除结点。
4.左子树的最大数据在左子树的最右侧,右子树的最大数据在右子树的最左侧,它们肯定至多只有一个孩子,所以可以按照只有一个孩子的情况删除。
综合这4点,有左右孩子的结点的删除就很简单了。
理解了原理,代码就简单了,不过还是有不少细节问题需要注意的,大家看我的注释就ok了
// BinarySearch.h
#pragma once
#include <iostream>
using namespace std;// K : key
template<class K>
struct BSTNode
{K _key;BSTNode<K>* _left;BSTNode<K>* _right;BSTNode(K key):_key(key),_left(nullptr),_right(nullptr){}
};template<class K>
class BSTree
{using Node = BSTNode<K>;
public:// 删除bool Erase(const K& key){// 这个判断其实无所谓,因为_root是空的话也进不去查找结点的循环,直接返回false了//if (_root == nullptr) return false;// 要删除结点,先查找这个结点,如果没有找到,cur最终会是nullptr,随后会跳出循环返回falseNode* cur = _root, * parent = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{// 找到了,删除// 没左孩子,左右孩子都没if (cur->_left == nullptr){// 根节点的情况if (cur == _root){_root = cur->_right;}// 非根节点else{// 链接parent和右孩子if (parent->_left == cur) parent->_left = cur->_right;else parent->_right = cur->_right;}// 两种情况都在最后删除结点delete cur;}// 没右孩子else if (cur->_right == nullptr){// 根节点if (cur == _root){_root = cur->_left;}//非根结点else{// 链接parent和左孩子,然后再delete掉curif (parent->_left == cur) parent->_left = cur->_left;else parent->_right = cur->_left;}// 删除结点delete cur;}// 左右孩子都有else{// 这里如果把replaceParent初始化为nullptr,那么就可能会出现没有进入循环,后面nullptr->_right的尴尬情况Node* replaceParent = cur;// 先右Node* replace = cur->_right;// 左左左左找右子树最小数据while (replace->_left){replaceParent = replace;replace = replace->_left;}// 把找到的结点数据给给curcur->_key = replace->_key;// 链接一下再删除// 这里的判断是必要的,因为看似我们向cur的右之后一直左左左左,那么应该一定是replaceParent->_left = replace->_right// 但其实如果刚开始replaceParent = cur,replace = cur->_right,压根就没进入循环,也就是cur的右孩子没有左孩子了,那么就应该replaceParent->_right = replace->_rightif (replaceParent->_right == replace) replaceParent->_right = replace->_right;else replaceParent->_left = replace->_right;// 删除“cur”delete replace;}return true;}}return false;}// 中序遍历void InOrder(){_InOrder(_root);cout << endl;}private:void _InOrder(Node* root){// 空指针不能->,判一下空if (root == nullptr) return;_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}private:Node* _root = nullptr;
};// Test.cpp
#include "BinarySearch.h"int main()
{BSTree<int> bst;int a[] = { 8, 3, 1, 10, 1, 6, 4, 7, 14, 13 };for (auto e : a){bst.Insert(e);}bst.InOrder();for (auto e : a){bst.Erase(e);bst.InOrder();}return 0;
}四、使用场景
1.key搜索场景
这个很好理解,就是在二叉搜索树中搜索有没有需要查找的K值,这里的K是指在二叉搜索树建立过程中比较大小用的key值。
比如小区的车库管理系统,系统识别出车的车牌号,并在存储此小区所有车主车牌号的二叉搜索树中搜索,如果找到了该车牌号,那么就抬杆,可以通过。如果没有找到,那么就不抬杆,不允许进入。这里的代表车牌号的字符串就是key,我们上面模拟实现的也是key搜索场景的二叉搜索树。

这是刚刚实现过的key搜索场景的整体代码,我把它用命名空间封装了一下,以便和key/value场景的区分:
// BinarySearch.h
#pragma once
#include <iostream>
using namespace std;namespace key
{// K : keytemplate<class K>struct BSTNode{K _key;BSTNode<K>* _left;BSTNode<K>* _right;BSTNode(K key):_key(key), _left(nullptr), _right(nullptr){}};template<class K>class BSTree{using Node = BSTNode<K>;public:// 查找bool Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key) cur = cur->_right;else if (cur->_key > key) cur = cur->_left;else return true;}return false;}// 插入bool Insert(const K& key){if (_root == nullptr){_root = new Node(key);return true;}// Node* newnode = new Node(key);// 在下面直接让cur变成新结点,就省去这一步了// 注意 *parentNode* cur = _root, * parent = _root;// 我们要实现的是不支持插入重复数据的元素的搜索二叉树,所以需要先查找while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else return false;}// 没有重复结点再插入cur = new Node(key);if (parent->_key > key) parent->_left = cur;else parent->_right = cur;return true;}// 删除bool Erase(const K& key){// 这个判断其实无所谓,因为_root是空的话也进不去查找结点的循环,直接返回false了//if (_root == nullptr) return false;// 要删除结点,先查找这个结点,如果没有找到,cur最终会是nullptr,随后会跳出循环返回falseNode* cur = _root, * parent = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{// 找到了,删除// 没左孩子,左右孩子都没if (cur->_left == nullptr){// 根节点的情况if (cur == _root){_root = cur->_right;}// 非根节点else{// 链接parent和右孩子if (parent->_left == cur) parent->_left = cur->_right;else parent->_right = cur->_right;}// 两种情况都在最后删除结点delete cur;}// 没右孩子else if (cur->_right == nullptr){// 根节点if (cur == _root){_root = cur->_left;}//非根结点else{// 链接parent和左孩子,然后再delete掉curif (parent->_left == cur) parent->_left = cur->_left;else parent->_right = cur->_left;}// 删除结点delete cur;}// 左右孩子都有else{// 这里如果把replaceParent初始化为nullptr,那么就可能会出现没有进入循环,后面nullptr->_right的尴尬情况Node* replaceParent = cur;// 先右Node* replace = cur->_right;// 左左左左找右子树最小数据while (replace->_left){replaceParent = replace;replace = replace->_left;}// 把找到的结点数据给给curcur->_key = replace->_key;// 链接一下再删除// 这里的判断是必要的,因为看似我们向cur的右之后一直左左左左,那么应该一定是replaceParent->_left = replace->_right// 但其实如果刚开始replaceParent = cur,replace = cur->_right,压根就没进入循环,也就是cur的右孩子没有左孩子了,那么就应该replaceParent->_right = replace->_rightif (replaceParent->_right == replace) replaceParent->_right = replace->_right;else replaceParent->_left = replace->_right;// 删除“cur”delete replace;}return true;}}return false;}// 中序遍历void InOrder(){_InOrder(_root);cout << endl;}private:void _InOrder(Node* root){// 空指针不能->,判一下空if (root == nullptr) return;_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}private:Node* _root = nullptr;};
}// Test.cpp
#include "BinarySearch.h"int main()
{key::BSTree<int> bst;int a[] = { 8, 3, 1, 10, 1, 6, 4, 7, 14, 13 };for (auto e : a){bst.Insert(e);}bst.InOrder();for (auto e : a){bst.Erase(e);bst.InOrder();}return 0;
}2.key/value搜索场景
这个也比较好理解,二叉搜索树建立过程中比较用的key值进行比较,而每一个结点中除了key值还有与key值相对应的value值,这个值可以是任何类型,一般来说都是表示和key相关联的属性。
就比如:
1.要统计一篇英语课文内出现的一些特定单词的出现次数,那么此时代表特定单词的字符串就是string,代表特定单词出现次数的就是value。建立一棵存储了这些特定单词的二叉搜索树,value都置为0,然后开始遍历这篇课文,把出现的每个单词都在该二叉搜索树中查找,如果找到了就value++,如果没有找到就不动。这样遍历下来,就会得到一个存储了特定单词在课文中出现次数的二叉搜索树,以后我们需要获取,只需要在这个二叉搜索树中搜索此单词,就能得到它在课文中出现的次数了。

2.商场地下停车场系统:key是车牌号,value是进入停车场的时间,车出停车场的时候,在树中搜索到该车牌号,然后用当前的时间减去value存的进入时间,计算得到需要支付的钱,然后付费成功后,再删除该车牌号的结点。
..............................
下面是key/value的代码,只需要在key的基础上略做修改即可,然后由于只有增删查的二叉搜索树还不是很完善,所以增添了拷贝构造和赋值重载以及析构函数。
// BinarySearch.h#pragma once
#include <iostream>
#include <algorithm>
using namespace std;namespace key_value
{// K : key, V:valuetemplate<class K, class V>struct BSTNode{K _key;V _value;BSTNode<K, V>* _left;BSTNode<K, V>* _right;BSTNode(K key, V value):_key(key),_value(value), _left(nullptr), _right(nullptr){}};template<class K, class V>class BSTree{using Node = BSTNode<K, V>;public:// 因为写拷贝构造了,这里强制生成一下其它构造BSTree() = default;// default,C++11,强制生成构造(所有)// 拷贝构造BSTree(const BSTree& bst){_root = Copy(bst._root);}// 析构~BSTree(){Destroy(_root);_root = nullptr;}// 赋值运算符重载// (现代写法)// 不能传const,传了就寄(bst._root)BSTree& operator=(BSTree bst){swap(_root, bst._root);return *this;}// 查找Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key) cur = cur->_right;else if (cur->_key > key) cur = cur->_left;else return cur;}return nullptr;}// 插入bool Insert(const K& key, const V& value){if (_root == nullptr){_root = new Node(key, value);return true;}Node* cur = _root, * parent = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else return false;}cur = new Node(key, value);if (parent->_key > key) parent->_left = cur;else parent->_right = cur;return true;}// 删除bool Erase(const K& key){Node* cur = _root, * parent = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{// 找到了,删除// 没左孩子,左右孩子都没if (cur->_left == nullptr){// 根节点的情况if (cur == _root){_root = cur->_right;}// 非根节点else{// 链接parent和右孩子if (parent->_left == cur) parent->_left = cur->_right;else parent->_right = cur->_right;}// 两种情况都在最后删除结点delete cur;}// 没右孩子else if (cur->_right == nullptr){// 根节点if (cur == _root){_root = cur->_left;}//非根结点else{// 链接parent和左孩子,然后再delete掉curif (parent->_left == cur) parent->_left = cur->_left;else parent->_right = cur->_left;}// 删除结点delete cur;}// 左右孩子都有else{// 这里如果把replaceParent初始化为nullptr,那么就可能会出现没有进入循环,后面nullptr->_right的尴尬情况Node* replaceParent = cur;// 先右Node* replace = cur->_right;// 左左左左找右子树最小数据while (replace->_left){replaceParent = replace;replace = replace->_left;}// 把找到的结点数据给给curcur->_key = replace->_key;// 链接一下再删除// 这里的判断是必要的,因为看似我们向cur的右之后一直左左左左,那么应该一定是replaceParent->_left = replace->_right// 但其实如果刚开始replaceParent = cur,replace = cur->_right,压根就没进入循环,也就是cur的右孩子没有左孩子了,那么就应该replaceParent->_right = replace->_rightif (replaceParent->_right == replace) replaceParent->_right = replace->_right;else replaceParent->_left = replace->_right;// 删除“cur”delete replace;}return true;}}return false;}// 中序遍历void InOrder(){_InOrder(_root);cout << endl;}private:// 要封装嘛所以返回新根节点给给public的拷贝构造Node* Copy(Node* root){// 后序拷贝(深)if (root == nullptr) return nullptr;// 要构造嘛肯定得链接一下Node* newRoot = new Node(root->_key, root->_value);newRoot->_left = Copy(root->_left);newRoot->_right = Copy(root->_right);return newRoot;}// 销毁void Destroy(Node* root){if (root == nullptr) return;// 先毁孩子再毁根,合理Destroy(root->_left);Destroy(root->_right);delete root;}void _InOrder(Node* root){// 空指针不能->,判一下空if (root == nullptr) return;_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}private:Node* _root = nullptr;};
}// Test.cpp
#include <string>
#include <vector>
using namespace std;#include "BinarySearch.h"int main()
{key_value::BSTree<string, int> kvbst;vector<string> v = { "apple","banana","wohaoshuai","youxiaxieyige","haha","haha","apple","banana","wohaoshuai","haha" };for (auto e : v){auto retNode = kvbst.Find(e);if (retNode) ++retNode->_value;else kvbst.Insert(e, 1);}string s;cin >> s;cout << s << "出现了" << kvbst.Find(s)->_value << "次" << endl;key_value::BSTree<string, int> copy(kvbst);key_value::BSTree<string, int> ass;ass = kvbst;copy.InOrder();ass.InOrder();copy.Erase("apple");ass.Erase("haha");kvbst.InOrder();copy.InOrder();ass.InOrder();return 0;
}完结撒花~~~~~~~
say顾拜~~~~~~~~~~~~~~~~~
“ψ(`∇´)ψ
相关文章:

C++进阶——二叉搜索树
目录 一、基本概念 二、性能分析 三、模拟实现 四、使用场景 1.key搜索场景 2.key/value搜索场景 一、基本概念 二叉搜索树(Binary Search Tree),看名字就知道,是可以用来搜索数据的一种二叉树。 它可以是空树(一个数据都…...

Require:业界优秀的HTTP管理方案。
方案异步JDK额外依赖特点HttpURLConnection 【优点】Java内置,简单易用。对于简单的HTTP请求和响应处理非常合适。 【缺点】功能相对较少,不支持现代特性(如异步请求、连接池等)。API相对繁琐,处理复杂请求时代码冗长。…...

装饰模式(Decorator Pattern)在 Go 语言中的应用
文章目录 引言什么是装饰模式?在Go语言中的应用定义接口实现具体逻辑创建装饰器使用装饰器 装饰模式 vs 中间件装饰模式中间件区别 总结 引言 在软件开发中,设计模式是解决常见问题的模板。装饰模式(Decorator Pattern)是一种结构…...

Windows系统部署redis自启动服务
文章目录 引言I redis以本地服务运行(Windows service)使用MSI安装包配置文件,配置端口和密码II redis服务以终端命令启动缺点运行redis-server并指定端口和密码III 知识扩展确认redis-server可用性Installing the Service引言 服务器是Windows系统,所以使用Windows不是re…...

34岁IT男的职场十字路口:是失业预警,还是转型契机?
在信息技术这片充满机遇与挑战的广袤领域,34岁,一个看似正值壮年却暗藏危机的年龄,成为了许多IT男性不得不面对的职场考验。当“34岁现象”逐渐凸显,我们不禁要问:在这个快速变化的时代,34岁的IT男…...

复试经验分享《三、计算机学科专业基础综合》- 数据结构篇
复试经验分享 三、计算机学科专业基础综合 3.1 数据结构 3.1.1 概念 时间复杂度 时间复杂度是指执行算法所需要的计算工作量一般情况下,按照基本操作次数最多的输入来计算时间复杂度,并且多数情况下我们去最深层循环内的语句所描述的操作作为基本操作…...

数学建模算法与应用 第16章 优化与模拟方法
目录 16.1 线性规划 Matlab代码示例:线性规划求解 16.2 整数规划 Matlab代码示例:整数规划求解 16.3 非线性规划 Matlab代码示例:非线性规划求解 16.4 蒙特卡洛模拟 Matlab代码示例:蒙特卡洛模拟计算圆周率 习题 16 总结…...
windows下安装、配置neo4j并服务化启动
第一步:下载Neo4j压缩包 官网下载地址:https://neo4j.com/download-center/ (官网下载真的非常慢,而且会自己中断,建议从以下链接下载) 百度网盘下载地址:链接:https://pan.baid…...

【JVM】—深入理解G1回收器—回收过程详解
深入理解G1回收器—回收过程详解 ⭐⭐⭐⭐⭐⭐ Github主页👉https://github.com/A-BigTree 笔记链接👉https://github.com/A-BigTree/Code_Learning ⭐⭐⭐⭐⭐⭐ 如果可以,麻烦各位看官顺手点个star~😊 文章目录 深入理解G1回收…...

2、CSS笔记
文章目录 二、CSS基础CSS简介CSS语法规范CSS代码风格CSS选择器CSS基础选择器标签选择器类选择器--最常用id选择器通配符选择器 CSS复合选择器交集选择器--重要并集选择器--重要后代选择器--最常用子代选择器--重要兄弟选择器相邻兄弟选择器通用兄弟选择器 属性选择器伪类选择器…...

使用XML实现MyBatis的基础操作
目录 前言 1.准备工作 1.1⽂件配置 1.2添加 mapper 接⼝ 2.增删改查操作 2.1增(Insert) 2.2删(Delete) 2.3改(Update) 2.4查(Select) 前言 接下来我们会使用的数据表如下: 对应的实体类为:UserInfo 所有的准备工作都在如下文章。 MyBatis 操作…...

智汇云舟亮相WAFI世界农业科技创新大会,并参编数字农业产业图谱
10月10日,2024WAFI世界农业科技创新大会农食行业创新与投资峰会在北京金海湖国际会展中心举行。中国农业大学MBA教育中心主任、教授付文阁、平谷区委常委、统战部部长刘堃、华为公共事业军团数字政府首席专家刘丹、荷兰瓦赫宁根大学前校长Aalt Dijkhuizen、牧原食品…...

昇思MindSpore进阶教程--数据处理性能优化(中)
大家好,我是刘明,明志科技创始人,华为昇思MindSpore布道师。 技术上主攻前端开发、鸿蒙开发和AI算法研究。 努力为大家带来持续的技术分享,如果你也喜欢我的文章,就点个关注吧 shuffle性能优化 shuffle操作主要是对有…...

Vivado - Aurora 8B/10B IP
目录 1. 简介 2. 设计调试 2.1 Physical Layer 2.2 Link Layer 2.3 Receiver 2.4 IP 接口 2.5 调试过程 2.5.1 Block Design 2.5.2 释放 gt_reset 2.5.3 观察数据 3. 实用技巧 3.1 GT 坐标与布局 3.1.1 选择器件并进行RTL分析 3.1.2 进入平面设计 3.1.3 收发器布…...

图(Java语言实现)
一、图的概念 顶点(Vertex):图中的数据元素,我们称之为顶点,图至少有一个顶点(非空有穷集合)。 边(Edge):顶点之间的关系用边表示。 1.图(Graph…...

GPT 生成绘画_Java语言例子_超详细
基于spring ai :简化Java AI开发,提升效率与维护性 过去在使用Java编写AI应用时,主要困境在于缺乏统一的标准化封装,开发者需要针对不同的AI服务提供商查阅各自独立的文档并进行接口对接,这不仅增加了开发的工作量&am…...

华为OD机试 - 小朋友分组最少调整次数 - 贪心算法(Python/JS/C/C++ 2024 E卷 100分)
华为OD机试 2024E卷题库疯狂收录中,刷题点这里 专栏导读 本专栏收录于《华为OD机试真题(Python/JS/C/C)》。 刷的越多,抽中的概率越大,私信哪吒,备注华为OD,加入华为OD刷题交流群,…...
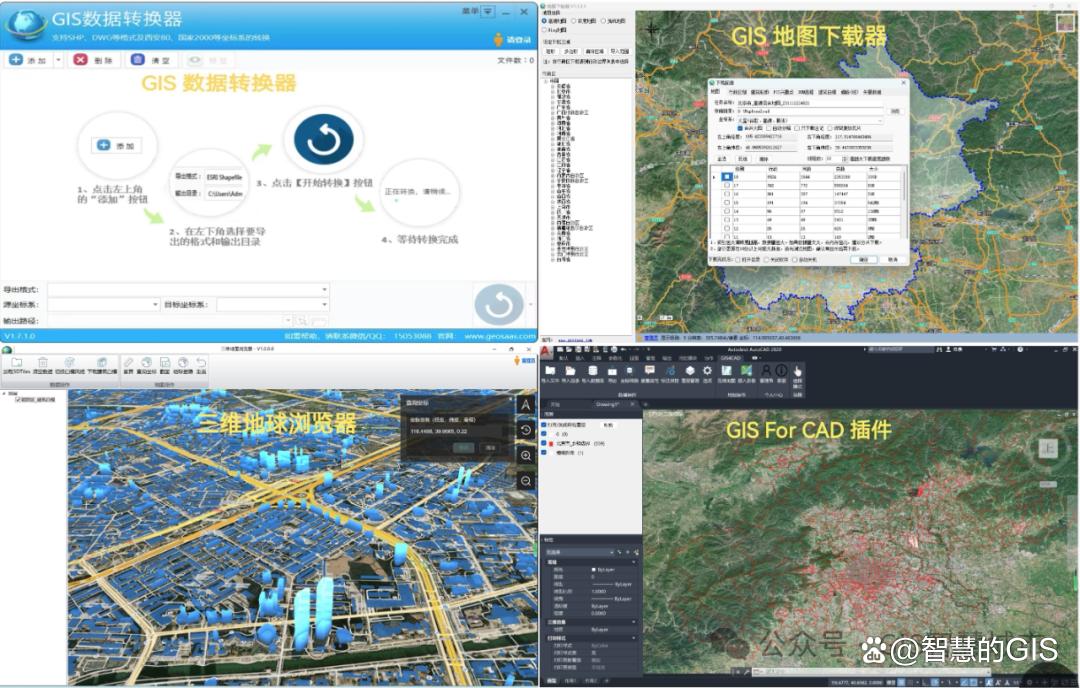
数字农业与遥感监测平台
随着全球人口的增长和气候变化的挑战,农业的可持续发展变得尤为重要。数字农业作为现代农业发展的重要方向,正逐渐成为提高农业生产效率、保障粮食安全的关键手段。遥感技术作为数字农业的重要组成部分,通过监测作物生长状况、土壤湿度、病虫…...

2023年12月中国电子学会青少年软件编程(Python)等级考试试卷(一级)答案 + 解析
一、单选题 1、下列程序运行的结果是?( ) print(hello) print(world) A.helloworld B.hello world C.hello world D.helloworld 正确答案:B 答案解析:本题考察的 Python 编程基础,print 在打印时…...

【优选算法】——双指针(下篇)!
🌈个人主页:秋风起,再归来~ 🔥系列专栏:C刷题算法总结 🔖克心守己,律己则安 目录 1、有效三角形的个数 2、查找总价值为目标值的两个商品 3、三数之和 4、四数之和 5、完结散花 1、有…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...
