【数据结构】栈和队列 + 经典算法题
目录
前言
一、栈
二、栈的实现
三、栈的循环遍历演示
四、栈的算法题
//
一、队列
二、队列的实现
三、使用演示
四、队列的算法题
总结

前言
本文完整实现了栈和队列的数据结构,以及栈和队列的一些经典算法题,让我们更加清楚了解这两种数据结构特点,并熟悉运用。
一、栈
栈:⼀种特殊的线性表,其只允许在固定的一端进行插⼊和删除元素操作。进行数据插入和删除操作的一端称为栈顶,另一端称为栈底。栈中的数据元素遵守后进先出LIFO(LastInFirstOut)的原则。
栈的特点:

压栈:栈的插入操作叫做进栈/压栈/入栈,入数据在栈顶。
出栈:栈的删除操作叫做出栈。出数据也在栈顶。


因为栈的特殊结构,所以对它的循环遍历也比较特殊。
栈 底层结构选型:
栈的实现一般可以使用数组或者链表实现,相对而言数组的结构实现更优一些。原因如下:
- 首先数组搭配栈顶下标top,可以很方便找到栈顶元素。当然使用链表也可以,链表采用带头单向不循环链表,采用头插和头删也能实现栈的基本操作,而且时间复杂度都是O(1)
- 不采用链表是因为栈的入栈和出栈操作频繁,链表需要不断开辟或者释放空间,而数组也采用动态开辟,使用2倍扩容能有效降低申请空间的频率。
- 其次链表结构每个节点都需要有一个指针变量,指针占用4/8字节,可能比储存的数据都大,会占用大量空间,而数组开辟的空间仅用于存储数据。
- 连续性空间比不连续空间访问速度快
二、栈的实现
1.栈的结构声明:
使用数组作为底层结构:
typedef int STDataType;
//定义栈结构
typedef struct Stack
{
STDataType* arr;
int capacity;//栈的空间大小
int top;//栈顶
}ST;
与顺序表基本相同,只有第三个成员变量含义不同。本质都是表示有效元素个数。
2.Stack.h头文件
#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <assert.h>typedef int STDataType;
//定义栈结构
typedef struct Stack
{STDataType* arr;int capacity;//栈的空间大小int top;//栈顶
}ST;//初始化
void STInit(ST* ps);//销毁
void STDesTroy(ST* ps);//入栈
void StackPush(ST* ps, STDataType x);//判空
bool StackEmpty(ST* ps);//出栈
void StackPop(ST* ps);//取栈顶元素
STDataType StackTop(ST* ps);//获取栈中有效元素个数
int STSize(ST* ps);栈的基本操作(函数)有:
- 栈的初始化
- 栈的销毁
- 入栈(增加元素)
- 出栈(删除元素)
- 判空(判断栈是否为空栈)
- 取栈顶元素(但不用出栈)
- 获取栈中的元素个数
3.Stack.c 定义文件
注意看注释,与顺序表很像
#include "Stack.h"//初始化
void STInit(ST* ps)
{assert(ps);//全初始化为空ps->arr = NULL;ps->capacity = ps->top = 0;
}//销毁
void STDesTroy(ST* ps)
{assert(ps);//判断arrif (ps->arr){free(ps->arr);}//销毁后置空ps->arr = NULL;ps->capacity = ps->top = 0;
}//入栈
void StackPush(ST* ps, STDataType x)
{assert(ps);//判断空间是否充足if (ps->top == ps->capacity){//使用三目操作符根据容量是否为0来选择如何给定新容量大小int newCapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;//1.如果容量为0,赋值4 2.如果容量不为零,进行二倍扩容//申请新空间STDataType* tmp = (STDataType*)realloc(ps->arr, newCapacity * sizeof(STDataType));if (tmp == NULL){perror("realloc fail!");exit(1);}//修改参数ps->arr = tmp;ps->capacity = newCapacity;}//空间充足ps->arr[ps->top++] = x;
}//判空
bool StackEmpty(ST* ps)
{assert(ps);return ps->top == 0;
}//出栈
void StackPop(ST* ps)
{assert(ps);//判断栈容量是否为空assert(!StackEmpty(ps));//直接让栈顶下移一位即可--ps->top;
}//取栈顶元素
STDataType StackTop(ST* ps)
{assert(ps);assert(!StackEmpty(ps));//判空//直接返回栈顶元素return ps->arr[ps->top - 1];
}//获取栈中有效元素个数
int STSize(ST* ps)
{assert(ps);return ps->top;
}函数解析:
- STInit函数:栈的初始化,需要传入栈的地址,将其 arr 初始化为空指针,capacity、top初始化为0。(assert是断言,一般的操作栈不能为空)
- STDesTroy函数:栈的销毁,传入栈的地址,栈的 arr 空间是由 realloc 申请的,因此需要free 释放,释放时应先判断 arr 是否申请了空间。释放后将栈的成员置空。
- StackPush函数:入栈,传入栈的地址和需要添加的元素。入栈之前需要先判断栈空间是否充足,通过栈结构的成员变量 capacity容量 和 top栈顶 是否相等来判断栈是否满了。因为我们初始化时并没有开辟空间,所以第一次入栈这里一定是需要开辟空间的,因此我们使用3目操作符对新容量大小进行赋值,如果容量为0那么就是第一次开辟空间,赋值4。如果不为0那么就进行2倍扩容。随后使用 realloc 开辟空间,判断成功开辟后,将新空间地址赋值给栈成员 arr,将新容量大小赋值给栈成员 capacity。
- StackEmpty函数:判空,传入栈的地址,如果栈顶下标都为0,那么栈就为空。
- StackPop函数:出栈,传入栈的地址,出栈需要判断栈是否为空,用写好的上一个函数判断即可,出栈操作只需要将栈顶下标减1,因为每次入栈也是在栈顶,下次入栈就会覆盖旧数据
- StackTop函数:取栈顶元素,传入栈的地址,先判断栈是否为空,然后直接返回栈顶元素即可。注意top的下标是下一个入栈的位置,因此栈顶元素需要-1。
- STSize函数:获取栈中有效元素个数,直接返回栈顶下标即可。
三、栈的循环遍历演示
#include "Stack.h"void StackTest1()
{//创建一个栈ST st;//初始化STInit(&st);//压入4个数据StackPush(&st, 1);StackPush(&st, 2);StackPush(&st, 3);StackPush(&st, 4);//循环遍历while (!StackEmpty(&st))//栈顶元素为空才停止{//取栈顶元素并打印printf("%d ", StackTop(&st));//出栈StackPop(&st);}//销毁STDesTroy(&st);
}int main()
{StackTest1();return 0;
}运行结果:

解析:
- 为什么只能这样遍历栈?
- 答:因为这样才符合栈的特性,栈是不支持随机访问的,它只能从栈顶开始访问。如果想访问下一个数据,那么上一个数据必须出栈才行。
四、栈的算法题
题目出处:
20. 有效的括号 - 力扣(LeetCode)


题目解析:
- 首先题目意思是判断一组括号是否符合语法规定,比如:{ [()] },当然题目中并没有规定括号优先级问题,所以小括号也能包住大括号
- 我们发现如果一开始是左括号,一旦遇到右括号,那么这个右括号如果是正确的,那么它一定和最近的左括号匹配
- 如何使用栈的特性来解决,栈是“先进后出”,如果我们让左括号先进栈,遇到右括号时,先取栈顶元素与右括号匹配,如果匹配,我们让左括号出栈。如此循环,左括号进栈,右括号判断,一旦匹配失败就说明括号字符串不符合规定。
- 如图:

题解:
bool isValid(char* s)
{//创建一个栈ST st;STInit(&st);//新建一个指针char* ps = s;//循环遍历while (*ps != '\0'){if (*ps == '(' || *ps == '[' || *ps == '{'){//入栈StackPush(&st, *ps);}else{//假如栈中无数据,一开始就是右括号if (StackEmpty(&st)){//直接销毁栈,并返回否STDesTroy(&st);return false;}//如果栈中有数据,先取栈顶元素,然后与右括号进行判断char ch = StackTop(&st);if (*ps == ')' && ch == '('|| *ps == ']' && ch == '['|| *ps == '}' && ch == '{'){//匹配正确,出栈StackPop(&st);}else{//匹配失败STDesTroy(&st);return false;}}++ps;}//如果栈中还有数据,证明左括号多了if (!StackEmpty(&st)){STDesTroy(&st);return false;}//一切正常STDesTroy(&st);return true;
}注意:答题时需要将栈的完整代码也加上去
///
一、队列
概念:只允许在⼀端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进先出FIFO(First In First Out)特性
特性:“先进先出” 或者 “后进后出”
入队列:进行插入操作的一端称为队尾
出队列:进行删除操作的一端称为队头

与栈的异同:
- 不同:栈是一端进行进出数据操作,队列是两端,一端进数据,一端出数据
- 相同:都是在端点操作
队列 底层结构选型:
队列也可以数组和链表的结构实现,使用链表的结构实现更优一些,因为如果使用数组的结构,出队列在数组头上出数据,效率会比较低。
二、队列的实现
1.队列的结构声明
typedef int QDatatype;//定义队列节点的类型结构
typedef struct QueueNode
{QDatatype data;struct QueueNode* next;
}QueueNode;//定义队列
typedef struct Queue
{QueueNode* phead;QueueNode* ptail;int size; //保存队列有效元素个数
}Queue;队列的结构比较特殊:
- 因为队列采用单链表作为底层结构,因此需要定义队列的存储数据类型,也就是定义每个数据的节点类型。
- 所以第一个结构体只是定义队列的元素类型,第二个结构体才是队列,队列仅需要两个指针,一个指针指向对头,一个指针指向队尾。因为这两指针类型都是元素节点的类型,所以要先定义元素类型
- 队列中的 size 成员是储存队列有效元素个数,因为如果想知道队列的元素个数,循环遍历队列效率低,因此队列多加一个成员变量储存元素个数。
2.Queue.h头文件
#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>typedef int QDatatype;//定义队列节点的类型结构
typedef struct QueueNode
{QDatatype data;struct QueueNode* next;
}QueueNode;//定义队列
typedef struct Queue
{QueueNode* phead;QueueNode* ptail;int size; //保存队列有效元素个数
}Queue;//初始化
void QueueInit(Queue* pq);//入队列
void QueuePush(Queue* pq, QDatatype x);//判空
bool QueueEmpty(Queue* pq);//出队列
void QueuePop(Queue* pq);//取队头数据
QDatatype QueueFront(Queue* pq);//取队尾数据
QDatatype QueueBack(Queue* pq);//队列有效元素个数
int QueueSize(Queue* pq);//销毁
void QueueDesTroy(Queue* pq);队列的常用操作:
- 队列的初始化
- 入队(插入元素)
- 出队(删除元素)
- 判空(判断队列是否为空)
- 取对头元素
- 取队尾元素
- 获取队列有效元素个数
- 队列的销毁
3.Queue.c定义文件
#include "Queue.h"//初始化
void QueueInit(Queue* pq)
{assert(pq);//初始化为空指针和0pq->phead = pq->ptail = NULL;pq->size = 0;
}//入队列
void QueuePush(Queue* pq, QDatatype x)
{assert(pq);//申请新节点QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));if (newnode == NULL){perror("malloc fail!");exit(1);}//赋值,初始化newnode->data = x;newnode->next = NULL;if (pq->phead == NULL){//如果队列为空pq->phead = pq->ptail = newnode;}else{//栈不为空pq->ptail->next = newnode;pq->ptail = pq->ptail->next;}//元素个数加一pq->size++;
}//判空
bool QueueEmpty(Queue* pq)
{assert(pq);return pq->phead == NULL && pq->ptail == NULL;
}//出队列
void QueuePop(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));//如果队列只有一个节点,要避免ptail成为野指针if (pq->phead == pq->ptail){free(pq->phead);pq->phead = pq->ptail = NULL;}else{//直接删除第一个节点QueueNode* next = pq->phead->next;free(pq->phead);pq->phead = next;}//元素个数减一pq->size--;
}//取队头数据
QDatatype QueueFront(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->phead->data;
}//取队尾数据
QDatatype QueueBack(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->ptail->data;
}//队列有效元素个数
int QueueSize(Queue* pq)
{assert(pq);return pq->size;
}//销毁
void QueueDesTroy(Queue* pq)
{assert(pq);//这一句判空可要可不要,写上的话在一些算法题中可能会报错//assert(!QueueEmpty(pq));QueueNode* pcur = pq->phead;while (pcur){QueueNode* next = pcur->next;free(pcur);pcur = next;}pq->phead = pq->ptail = NULL;pq->size = 0;
}函数解析:
- QueueInit函数:队列的初始化,传入队列的地址,将其头指针和尾指针都初始化为NULL,size 初始化为0。
- QueuePush函数:入队,传入队列的地址和需要插入的数据,首先申请新节点,将需要出入的数据赋值给新节点,并将其 next 指针初始化为空。然后从队尾插入队列,在插入队列之前需要先判断队列是否为空(可以将判空函数提前),因为如果队列为空,那么它的头尾指针都应是新节点,如果队列不为空,那么从队尾插入,先将队尾指针的 next 指针指向新节点,然后更新队尾指针为新节点,最后不要忘了让 size++。
- QueueEmpty函数:判空,直接返回头指针与空指针的判断结果,判不判断尾节点都行
- QueuePop函数:出队,出队列需要先判空,另外还需要注意,如果队列只有一个元素,那么尾指针和头指针都需要变为空指针。如果队列元素多于一个元素,那么只改变头指针即可,先保存头指针的 next 节点,然后释放头指针节点,再跟新头指针,最后记得让 size--。
- QueueFront函数:取对头元素,有头指针存在,判空后,直接返回头指针指向的节点数据
- QueueBack函数:取队尾元素,同理,返回尾指针指向的节点数据即可
- QueueSize函数:获取队列有效元素个数,返回队列结构成员 size 即可
- QueueDesTroy函数:队列的销毁,判空可不写,先保存头指针,然后循环遍历释放各节点,如果不判空这里不受影响,因为空队列那么头指针也为空,就不会进入循环,最后将指针和 size 都置空或置0。
三、使用演示
#include "Queue.h"void QueueTest1()
{//创建队列Queue q;//初始化QueueInit(&q);//入队QueuePush(&q, 1);QueuePush(&q, 2);QueuePush(&q, 3);QueuePush(&q, 4);//循环出队列并打印while (!QueueEmpty(&q)){//取队头元素printf("%d ", QueueFront(&q));//出队列QueuePop(&q);}//销毁QueueDesTroy(&q);
}int main()
{QueueTest1();return 0;
}运行结果:

注意:将销毁队列中的判空注释掉,不然会报错
四、队列的算法题
1.双队列实现栈
题目出处:225. 用队列实现栈 - 力扣(LeetCode)



题目解析:
- 题目是让我们使用两个队列来实现栈,满足栈的“先进后出”,实现6种基本操作

- 如何实现,队列的特性是“先进先出”,一端进数据,一端出数据,那么假如我们将数据 1、2、3 插入队列1,我们需要出栈,那么只能出数据3,而队列只能在对头出数据,因此我们先将数据 1、2 出队列并插入队列2,此时队列2中为数据 1、2,队列1中数据为 3。此时我们再将队列1中的3出队列,此时就完成了出栈的操作。
- 所以我们使用将数据在两个队列中来回导的方法,实现栈的操作方法。
- 那么这里面的关键就是,每一次操作后只有一个队列中有数据,另一个队列为空。
- 入栈操作:我们往不为空的队列中插入数据。
- 出栈操作:找到不为空的队列,把不为空队列中的 size-1 个数据导到空队列中,最后将不为空队列中的最后一个数据出队列
- 注意取栈顶元素操作不能模仿出栈操作,因为取栈顶元素不会出栈,来回导会造成两个队列都不为空的情况
题解:
注意:在答题时需将队列的完整代码写上去
typedef struct
{//栈结构使用两个队列Queue q1;Queue q2;
} MyStack;//初始化
MyStack* myStackCreate()
{动态开辟栈的空间MyStack* pst = (MyStack*)malloc(sizeof(MyStack));//两个队列使用队列初始化函数完成初始化QueueInit(&pst->q1);QueueInit(&pst->q2);return pst;
}//入栈
void myStackPush(MyStack* obj, int x)
{//往不为空的队列中入数据if (!QueueEmpty(&obj->q1)){QueuePush(&obj->q1, x);}else{QueuePush(&obj->q2, x);}
}//出栈
int myStackPop(MyStack* obj)
{//首先找不为空的队列Queue* empQ = &obj->q1;Queue* noneQ = &obj->q2;if (!QueueEmpty(&obj->q1)){empQ = &obj->q2;noneQ = &obj->q1;}//将不为空的队列中的size-1个数据导入到空队列while (QueueSize(noneQ) > 1){int Front = QueueFront(noneQ);QueuePush(empQ, Front);QueuePop(noneQ);}//非空队列剩下的一个数据就是需出栈的数据int pop = QueueFront(noneQ);QueuePop(noneQ);return pop;
}//取栈顶元素
int myStackTop(MyStack* obj)
{//找到不为空的队列,返回队尾元素即可if (!QueueEmpty(&obj->q1)){return QueueBack(&obj->q1);}else{return QueueBack(&obj->q2);}
}//判空
bool myStackEmpty(MyStack* obj)
{return QueueEmpty(&obj->q1) && QueueEmpty(&obj->q2);
}//销毁
void myStackFree(MyStack* obj)
{QueueDesTroy(&obj->q1);QueueDesTroy(&obj->q2);free(obj);obj = NULL;
}2.双栈实现队列
题目出处:232. 用栈实现队列 - 力扣(LeetCode)


题目解析:
- 与上一题相反,这题需要使用两个栈来实现队列结构

- 有了上一题的经验,这一题同样也是使用来回导数据的方式。
- 如我们现在需要入队数据 1、2、3,我们将其插入栈1中,栈是“先进后出”,当我们需要出队时,我们直接将栈1的数据出栈并插入栈2,此时栈2中的数据为 3、2、1,而栈顶元素 1 就是我们需要出队的数据,也就是对头元素。接下来如果我们还需要出队,那么直接让栈2元素出栈即可,如果需要入队元素,直接插入到栈1

- 因此,与上一题不同的是,这次我们不用保证有一个容器为空,我们让栈1专门存放入队元素,让栈2专门用来出对。这样也就符合了队列的“先进先出”特性
题解:
typedef struct
{ST pushST;//用于入队ST popST;//用于出队
} MyQueue;//初始化
MyQueue* myQueueCreate()
{MyQueue* pq = (MyQueue*)malloc(sizeof(MyQueue));//调用栈自己的初始化函数STInit(&pq->popST);STInit(&pq->pushST);return pq;
}//入队
void myQueuePush(MyQueue* obj, int x)
{//直接往push栈中插入元素StackPush(&obj->pushST, x);
}//出队
int myQueuePop(MyQueue* obj)
{//先判断pop栈是否为空if (StackEmpty(&obj->popST)){//为空,导数据while (!StackEmpty(&obj->pushST)){//将push栈中元素全导入pop栈StackPush(&obj->popST, StackTop(&obj->pushST));StackPop(&obj->pushST);}}//先储存出队元素,出栈后返回int pop = StackTop(&obj->popST);StackPop(&obj->popST);return pop;
}//取对头元素
int myQueuePeek(MyQueue* obj)
{//前面与出队操作一致if (StackEmpty(&obj->popST)){//导数据while (!StackEmpty(&obj->pushST)){StackPush(&obj->popST, StackTop(&obj->pushST));StackPop(&obj->pushST);}}//最后不用出栈,直接返回栈顶元素return StackTop(&obj->popST);
}//判空
bool myQueueEmpty(MyQueue* obj)
{return StackEmpty(&obj->popST) && StackEmpty(&obj->pushST);
}//销毁
void myQueueFree(MyQueue* obj)
{STDesTroy(&obj->popST);STDesTroy(&obj->pushST);free(obj);obj = NULL;
}
3.设计循环队列
题目出处:622. 设计循环队列 - 力扣(LeetCode)


题目解析·:
- 题目是让我们设计一个循环队列,那么什么是循环队列,根据题目我们了解循环队列依旧遵循“先进先出”特性,结构上是队列的尾指针与头指针相连,并且重要的是循环队列的空间的固定的。
- 如何设计呢,既然循环队列空间是一定的,那我们可以采取数组作为底层结构,当然链表也行,不过数组更为方便,能一次性开辟完空间。除了底层结构,我们知道队列是有两个指针指向队头和对尾的,那么我们就可以设置两个下标 front 和 rear 来分别指向循环队列的对头和队尾。
- 循环队列还有插入和删除操作,执行这两个操作时我们需要判断循环队列是否满了或者空了,那么我们怎么判断呢,假如我们将 front 和 rear 都初始化为0,那么当它俩相等时,我们可以确定队列为空,可是队列满了它们俩也相等。怎么解决这个问题呢
- 直接说结论吧,我们选择多开辟一个空间,也就是数组的最后一位,最后一个空间不存储数据,当 rear 走到这个位置时,那么此时循环队列就满了,而 front 和 rear 下标也就不相同。这样就可以通过下标来区分循环队列是空是满。满了的公式由 rear+1 等于 front 的下标推导,因为循环队列中下标走到头了后需要回到对头,所以使用取余来更新计算下标,推出以下公式

- 能够判断队列状态后,我们就可以进行入队和出队操作了。
- 入队操作:首先根据公式判断队列是否满了,满了直接返回 false,没满,在 rear 处插入数据,然后 rear++ 往后走一位,这时候就需要注意了,rear 不能越界,走到数组末尾了,如果队列还有空间,需要更新 rear 的下标,所以 rear = rear % (capacit+1),保证下标循环走动
- 出队操作:需要先判空,判空后如果队列不为空,直接让 front++,使原数据无效即可,这里front 的下标同样不能越界,需要通过取余来保证其在队列中循环走动,front %= capacity+1
- 获取对头和对尾元素中,对头元素获取简单,判空后直接返回 front 下标位置处的数据即可,而队尾就有所不同,判空后,不能直接返回 rear 下标处的数据,因为 rear 下标指向的是下一个元素插入的位置,取队尾元素时需减1,因此有一种特殊情况:

- 即当 rear 刚好处于下标为0处的位置,这时候返回队尾元素 3 时,不能直接返回 rear-1 处下标的元素,而是另外创建一个 prev 指针,让其指向 rear-1 处的下标,并判断如果 rear 刚好处于下标为0的位置时,让 prev 等于 capacity ,也就是下标为5的位置。
题解:
typedef struct
{int* arr;int front;int rear;int capacity;
} MyCircularQueue;//初始化
MyCircularQueue* myCircularQueueCreate(int k)
{MyCircularQueue* pst = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));pst->arr = (int*)malloc(sizeof(int) * (k + 1));pst->front = pst->rear = 0;pst->capacity = k;return pst;
}//判断队列是否满了
bool myCircularQueueIsFull(MyCircularQueue* obj)
{return (obj->rear + 1) % (obj->capacity + 1) == obj->front;
}//插入数据
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value)
{//如果队列满了if (myCircularQueueIsFull(obj)){return false;}//没满obj->arr[obj->rear++] = value;obj->rear %= obj->capacity + 1;return true;
}//判空
bool myCircularQueueIsEmpty(MyCircularQueue* obj)
{return obj->front == obj->rear;
}//删除数据
bool myCircularQueueDeQueue(MyCircularQueue* obj)
{//如果队列为空if (myCircularQueueIsEmpty(obj)){return false;}//不为空obj->front++;obj->front %= obj->capacity + 1;return true;
}//获取对头元素
int myCircularQueueFront(MyCircularQueue* obj)
{if (myCircularQueueIsEmpty(obj)){return -1;}return obj->arr[obj->front];
}//获取队尾元素
int myCircularQueueRear(MyCircularQueue* obj)
{if (myCircularQueueIsEmpty(obj)){return -1;}int prev = obj->rear - 1;if (obj->rear == 0){prev = obj->capacity;}return obj->arr[prev];
}//销毁
void myCircularQueueFree(MyCircularQueue* obj)
{free(obj->arr);free(obj);obj = NULL;
}扩展:计算循环队列有效元素个数
公式:循环队列有效元素个数 = ( rear - front + capacity +1 ) % ( capacity + 1 )
总结
以上就是本文的全部内容,感谢支持!
相关文章:

【数据结构】栈和队列 + 经典算法题
目录 前言 一、栈 二、栈的实现 三、栈的循环遍历演示 四、栈的算法题 // 一、队列 二、队列的实现 三、使用演示 四、队列的算法题 总结 前言 本文完整实现了栈和队列的数据结构,以及栈和队列的一些经典算法题,让我们更加清楚了解这两种数据…...

C# 基于winform 使用NI-VISA USB口远程控制电源 万用表
1.下载完整版本NI-VISA NI-VISA Download - NI *注意支持的操作系统,以便后期编译 安装完成之后,打开NI MAX,插上usb口,打开测试面板进行通信 2.编程示例 见本地文件夹C:\Users\Public\Documents\National Instruments\NI-VIS…...

Python设计方差分析实验
前言 方差分析(ANOVA)是一种用于检测多个样本均值之间差异的统计方法,广泛应用于实验设计与数据分析中。通过分析不同因素对实验结果的影响,方差分析能够帮助评估哪些因素显著影响了实验结果,并且可以提供各因素交互作用的深入理解。在多因子实验设计中,随机化、重复和平…...

【Oracle DB故障分享】分享一次由于SGA设置太小导致的DP备份失败
List item 今天给客户做Oracle例行数据库健康巡检,过程中检出一些备份异常,分享如下。 排查问题: 打开DP备份软件,随即弹出如下提示: 登录DP,查看备份情况:发现从10/6开始,DP备份…...

Yocto构建教程:在SDK中添加Qt5并生成带有Qt5的SDK
下载meta-qt5 复位环境 确认下版本是否匹配 添加meta-qt5进bblayers.bb 先编译起来 研究meta-qt5 构建带有Qt5的toolchain SDK meta-toolchain如何编译带Qt5的软件包? 文件系统中如何添加Qt5软件包 如何同时编译目标镜像和SDK Yocto Project是一个开源的嵌…...

操作系统——位示图
这里写目录标题 前言基础说明相关计算题目一题目二题目三 前言 基础说明 位示图是一种用来表示文件和目录在磁盘上存储位置的图形化表示方法。它通过使用一系列的位来表示文件或目录所占用的磁盘块,从而显示出磁盘上的存储情况。 位示图通常是一个位向量…...

【STM32 Blue Pill编程实例】-矩阵键盘
矩阵键盘 文章目录 矩阵键盘1、矩阵键盘介绍2、硬件准备与接线3、模块配置3.1 矩阵键盘列引脚配置3.2 矩阵键盘列引脚配置3.3 LED配置4、代码实现在本文中,我们将介绍如何把 43 键盘与 STM32 Blue Pill 连接,并使用 HAL 库在 STM32CubeIDE 中对其进行编程。 键盘是一种输入设…...

基于SSM的药品商城系统
作者:计算机学姐 开发技术:SpringBoot、SSM、Vue、MySQL、JSP、ElementUI、Python、小程序等,“文末源码”。 专栏推荐:前后端分离项目源码、SpringBoot项目源码、Vue项目源码、SSM项目源码、微信小程序源码 精品专栏:…...

南京邮电大学电工电子A实验十一(数据选择器及逻辑电路的动态测试)
文章目录 一、实验报告预览二、Word版本报告下载 一、实验报告预览 二、Word版本报告下载 点我...

算法.图论-BFS及其拓展
文章目录 广度优先搜索简介经典bfs习题地图分析贴纸拼词 01bfs解析基本过程相关习题 广度优先搜索简介 bfs的特点是逐层扩散, 从源头到目标点扩散了几层, 最短路就是多少 bfs的使用特征是任意两个节点的距离(权值)是相同的(无向图, 矩阵天然满足这一特点) bfs开始的时候可以是…...

mongodb的相关关键字说明
以下是MongoDB中一些数据库相关的关键字说明: 1. 数据库(Database) 概念 数据库是MongoDB中数据存储的最高层级容器,类似于关系型数据库中的数据库概念。一个MongoDB服务器实例可以包含多个数据库,每个数据库可以有自…...
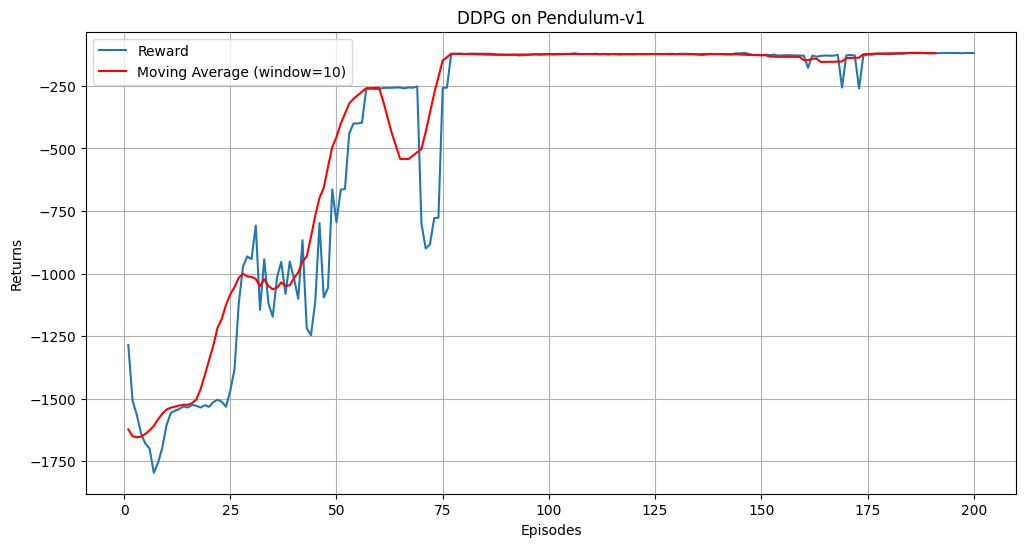
强化学习之DDPG算法
前言: 在正文开始之前,首先给大家介绍一个不错的人工智能学习教程:https://www.captainbed.cn/bbs。其中包含了机器学习、深度学习、强化学习等系列教程,感兴趣的读者可以自行查阅。 一、算法介绍 深度确定性策略梯度 ࿰…...

【进阶OpenCV】 (16)-- 人脸识别 -- FisherFaces算法
文章目录 FisherFaces算法一、算法原理二、算法优势与局限三、算法实现1. 图像预处理2. 创建FisherFace人脸特征识别器3. 训练模型4. 测试图像 总结 FisherFaces算法 PCA方法是EigenFaces人脸识别的核心,但是其具有明显的缺点,在操作过程中会损失许多人…...

电脑主机配置
显卡: 查看显卡:设备管理器--显示适配器 RTX4060 RTX和GTX区别: GTX是NVIDIA公司旧款显卡,RTX比GTX好但是贵 处理器CPU: Intel(R) Core(TM) i5-10400F CPU 2.90GHz 2.90 GHz 10400F:10指的是第几代…...
图书借阅小程序开源独立版
图书借阅微信小程序,多书馆切换模式,书馆一键同步图书信息,开通会员即可在线借书,一书一码书馆员工手机扫码出入库从会员到书馆每一步信息把控图书借阅小程序,让阅读触手可及在这个快节奏的时代,你是否渴望…...

flutter TextField限制中文,ios自带中文输入法变英文输入问题解决
由于业务需求,要限制TextField只能输入中文,但是测试在iOS测试机发现自带中文输入法会变英文输入问题,安卓没有问题,并且只有iOS自带输入法有问题,搜狗等输入法没问题。我们目前使用flutter2.5.3版本,高版本…...

ThreadLocal的应用场景
ThreadLocal介绍 ThreadLocal为每个线程都提供了变量的副本,使得每个线程访问各自独立的对象,这样就隔离了多个线程对数据的共享,使得线程安全。ThreadLocal有如下方法: 方法声明 描述public void set(T value)设置当前线程绑定的…...

Python--plt.errorbar学习笔记
plt.errorbar 是 Matplotlib 库中的一个函数,用于绘制带有误差条的图形。下面给出的代码行的详细解释: import numpy as np from scipy.special import kv, erfc from scipy.integrate import dblquad import matplotlib.pyplot as plt import scipy.in…...

文件信息类QFileInfo
常用方法: 构造函数 //参数:文件的绝对路径或相对路径 [explicit] QFileInfo::QFileInfo(const QString &path) 设置文件路径 可构造一个空的QFileInfo的对象,然后设置路径 //参数:文件的绝对路径或相对路径 void QFileI…...

堆排序(C++实现)
参考: 面试官:请写一个堆排序_哔哩哔哩_bilibiliC实现排序算法_c从小到大排序-CSDN博客 堆的基本概念 堆排实际上是利用堆的性质来进行排序。堆可以看做一颗完全二叉树。 堆分为两类: 最大堆(大顶堆):除根…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...
