【隐私计算】隐语HEU同态加密算法解读

HEU: 一个高性能的同态加密算法库,提供了多种 PHE 算法,
包括ZPaillier、FPaillier、IPCL、Damgard Jurik、DGK、OU、EC ElGamal 以及基于FPGA和GPU硬件加速版本的Paillier版本。
本文我们会基于GPU运行HEU Docker容器,编译打包GPaillier并测试其性能。
算法总览

算法分类
Paillier
Paillier 算法由 Pascal Paillier 在 1999 年提出,参见:算法详情(跳转维基百科)
| 算法类型 | 加法同态加密 |
| 安全性 | IND-CPA 安全,语义安全(Semantic Security) |
| 困难假设 | 判定性复合剩余假设 decisional composite residuosity assumption (DCRA) |
| 安全强度(Security Strength) | 2048 位密钥长度等于或略低于 112 bits 安全强度 3072 位密钥长度等于或略低于 128 bits 安全强度 |
关于安全强度
目前未有直接的文献表明 DCRA 密钥长度与安全比特位数之间的关联,一般认为的难度 DCRA <= FACTORING(因数分解)<= DLP in
[1],在 DLP(离散对数难题)中,2048 group size 对应 112 bits,3072 group size 对应 128 bits [2],因此 Paillier 的安全强度等效或略低于这个数值。
- ZPaillier 中的 Z 与数学中表示整数的
含义相同,即实现了一套支持整数运算的 Paillier 算法。
- 实现基于的 Paper:
- FPaillier 中的 F 表示浮点数
,Paillier 算法本身只支持整数,FPaillier 对Paillier 做了扩展,使其可以支持浮点数。
- FPaillier 的算法原理与 Python-Paillier 库类似。
-
IPCL 全称 Intel Paillier Cryptosystem Library,是 Intel 贡献的一种 Paillier 算法实现,其特点是支持 AVX512-IFMA 指令集和 Intel QAT 硬件加速器加速。
-
实现基于的代码库:pailliercryptolib 。
-
| SchemaType 参数名称 | phe.SchemaType.ZPaillier | phe.SchemaType.FPaillier | phe.SchemaType.IPCL |
| 实现算法 | Paillier | Paillier | Paillier |
| 稳定性 | 稳定 | 稳定 | 实验性质,仅供测试和评估目的,还在持续完善中 |
| 支持的平台 | Linux,macOS(Intel & Arm) | Linux,macOS(Intel & Arm) | Linux,macOS(Intel) |
| 是否依赖特定硬件 | 不依赖 | 不依赖 | 不依赖 |
| 是否支持硬件加速 | 不支持 | 不支持 | 支持 AVX512-IFMA 指令集和/或 Intel QAT 加速器 |
| 相对性能 | 高 | 低 | 高 |
Okamoto-Uchiyama
Okamoto-Uchiyama 算法由 Tatsuaki Okamoto 和 Shigenori Uchiyama 在 1998 年提出,参见:算法详情(跳转维基百科)
| 算法类型 | 加法同态加密 |
| 安全性 | IND-CPA 安全,语义安全(Semantic Security) |
| 困难假设 | p-subgroup assumption |
| 安全强度(Security Strength) | 存在争议,相同的密钥长度下 OU 的强度比特与 Paillier 相同或略低,见下文解释 |
关于安全强度
Paillier 的
,而 OU 的
,当 n 长度相同时两者安全强度是否相同,存在不同的观点。OU 的原始论文 [3] 认为目前最快的因式分解算法是 Field sieve method,这种算法的复杂度只和 n 相关,因此只要对齐 n 就可以得到相同的安全强度。
但也有一些 Paper 认为 OU 的 n 需要比 Paillier 多 500~600 比特两者安全性才相等 [4],甚至还有文章 [5] 说 n 的分解只与 p 相关。因此如果特别在意安全性,请适当加大 OU 密钥长度。
| SchemaType 参数名称 | phe.SchemaType.OU |
| 实现算法 | Okamoto-Uchiyama |
| 稳定性 | 稳定 |
| 支持的平台 | Linux,macOS(Intel & Arm) |
| 是否依赖特定硬件 | 不依赖 |
| 是否支持硬件加速 | 不支持 |
| 相对性能 | 高 |
OU 与 Paillier 比较
- 选择明文攻击 Chosen-Plaintext Attack (CPA)
- 选择密文攻击 Chosen-Ciphertext Attack (CCA)
OU 的优点:
- 相同的使用场景下,OU 的计算性能远高于 Paillier。
- 相同的使用场景下,OU 的密文大小只有 Paillier 的一半。假设密钥长度为 N,则 Paillier 的密文大小为 2N 比特,而 OU 密文为 N 比特。
- OU 的安全性与 Paillier 相同,两者都达到了 IND-CPA 安全,且都不满足 IND-CCA 安全。
OU 的缺点:
- OU 在学术上的知名度不如 Paillier。
- OU 的明文值域空间不明确。假设密钥长度为 N,则 Paillier 的明文值域空间为
,而 OU 的明文值域空间为
,其中 p 是 private key 中的参数,因此 OU 的值域空间不是公开的。
- 虽然理论上两者都不满足 IND-CCA 安全定义,但在实际 IND-CCA 场景下 OU 存在已知攻击,而 Paillier 暂未发现有效攻击。
风险提示
虽然 OU 与 Paillier 在学术上的安全级别相同,两者都满足 IND-CPA 安全,且都达不到 IND-CCA 安全,但实际情况是 OU 已经被发现有高效的攻击手段,而 Paillier 尚未发现有效攻击。
OU 明文空间溢出攻击
OU 的明文空间为
,即 OU 的密文解密以后存在 mod p 的效果。如果允许攻击者加密一个大于 p 的明文,则容易反推出 p,导致私钥泄漏,具体原理如下:
- 攻击者选择一个比 p 大的明文:
,进行加密,并且能够得到解密结果
。
- 显然:
,并且:
。
- 通过计算最大公约数
即可得到 p。
OU 在实现时一般做了限制,不允许直接加密大于 p 的明文,但是由于 OU 支持密态加法和明密文乘法,上述溢出攻击仍旧是可能的:
- 攻击者选择一个接近但是小于 p 的明文 m 加密得到 c。
- 对该密文 c 执行 t 次密文加法(或一次明密文乘法)满足
,然后解密得到
。
- 攻击者获取
,利用同余关系即可获取私钥 p。
攻击防御
上述攻击成立的关键有两点,一是攻击者需要能构造出一个大于 p 的密文,二是攻击者需要能获取解密的结果,两者缺一不可,这是一个典型的选择密文攻击(CCA)场景,实际使用 OU 时,应当 避免在 CCA 成立的场景下使用 OU。
(1) 安全使用Case1
对于一些简单的场景,比如 Alice、Bob 两方计算,假设 Alice 有私钥,Bob 为恶意参与方,计算的过程为 Alice 将数据加密后发给 Bob 计算,Bob 把计算结果返回给 Alice,此时,即使 Bob 构造了恶意的密文 c,但是 Bob 拿不到 c 对应的解密结果,Bob 的攻击会造成计算错误,但是密钥不会泄露。
(2) 安全使用Case2
在一些复杂的隐私计算场景中,下一轮的交互取决于上一轮交互的结果,CCA 场景成立也许是不可避免的,但并非说明 OU 就一定无法使用,如果 Alice 有有效的手段阻断攻击,OU 仍旧可以选用。让我们再来回顾一下攻击的过程:Bob 构造的密文 c 对应明文 m,Alice 解密后得到 m′=m mod p,实际的问题是,m′有可能非常大,远超一般业务中使用的 int64 所能表达的范围,因为 Bob 想要构造一个略大于 p 的密文是非常困难的,p 一般非常大,key size 为 2048 时 p 大约为 682bits,Bob 盲猜一个数 m 满足
,其概率小于
,即盲猜的 m 的高618bits 与 p 完全一样,这个概率是可以忽略不计的,因此可以认为 m′ 仍旧是一个大数,当 Alice 解密发现明文不在合理值域范围时,可以拒绝 Bob 的结果,从而阻止 Bob 的攻击。
所以对于联邦逻辑回归中,一般是在梯度计算的时候,涉及到密文计算,但梯度的值一般是有范围限制的,比如标准化后的特征值取值范围通常是在-3到3之间;归一化后的特征值去值范围在0到1之间;梯度因子
的大小,由于
需要进行sigmoid转化,因此
通常在(0, 1)之间,而标签
通常为[0,1],所以梯度因子的范围(-1, 1), 另外,host方加入的随机噪声通常可控,如果恶意设置过大,Guest方解密后可以直接拒绝。从而阻止Host方的攻击。
ElGamal
ElGamal 是一个基于 Diffie–Hellman 密钥交换的非对称加密算法,由 Taher Elgamal 在 1985 年提出[6]。原始的 ElGamal 具有乘法同态性质,其同态性来自于密文块 。
在之后的 Generalized ElGamal 算法中,整个密码体制被定义在循环群 G 上,其加密的安全性也取决于 G 上离散对数问题的困难性,为此,用于构建 Generalized ElGamal 的循环群 G 必须满足以下两项要求:
- 高效性:G 上的计算必须非常快速
- 安全性:求解 G 上的离散对数问题(DLP)非常困难
以下是一些满足上述要求的具体的 G 的例子:

| 算法类型 | 同态特性取决于底层循环群 G 的定义,根据 G 的不同 Elgamal 可能为加法同态、乘法同态或没有同态特性。 |
| 安全性 | 如果定义在 G 上的 Decisional Diffie–Hellman assumption (DDH) 是困难的,则算法是语义安全(Semantic Security)的,不可区分性满足 IND-CPA |
| 困难假设 | CDH & DDH |
| 安全强度(Security Strength) | 取决于 G |
为了获得加法同态特性,以及兼顾计算上的高效性,HEU将循环群选定为椭圆曲线点群(EC Group)作为 ElGamal 底层的 G,因此 HEU 中的 ElGamal 也称为 EC ElGamal。取决于明文到 EC Group 的映射方式,如果映射妥当,则 EC ElGamal 满足加法同态特性。
HEU 实现了 EC ElGamal 算法,这是一种定义在椭圆曲线点群(EC Group)上的 ElGamal 算法,相比其他循环群 G,EC Group 的计算效率更高,使得 EC ElGamal 最终性能表现非常优秀。
另一方面,为了维持加法同态特性,EC ElGamal 将明文映射到 EC Group 的方式为:m′=mG,其中 mm 是明文,m′是映射后的明文,即椭圆曲线上的一个点,G 是 EC Group 的生成元。这是一个典型的单向函数(one-way function),EC ElGamal 解密之后得到 m′ 想要反向计算出真正的明文 mm 是非常困难的,没有直接求解算法,以至于 EC ElGamal 解密非常慢,这是 EC ElGamal 的缺点。
| SchemaType 参数名称 | phe.SchemaType.ElGamal |
| 实现算法 | ElGamal |
| 同态特性 | 加法同态加密 |
| 稳定性 | 仅供非生产环境使用 |
| 支持的平台 | Linux,macOS |
| 是否依赖特定硬件 | 不依赖 |
| 是否支持硬件加速 | 取决于曲线种类的选择。(注:目前所有曲线都不支持硬件加速) |
| 相对性能 | 高 |
算法性能
HEU 提供了一个 Benchmark 用以测试每个算法的性能,若要运行 Benchmark 请先 clone HEU 代码库,然后在项目根目录下执行:
# 测试算法在 scalar 运算场景下的性能
# Test the performance of algorithms in scalar computing scenarios
bazel run -c opt heu/library/benchmark:phe -- --schema=zpaillier# 测试算法在矩阵运算场景下的性能
# Test the performance of algorithms in matrix operation scenarios
bazel run -c opt heu/library/benchmark:np -- --schema=zpaillier- Key size = 2048
表格的项表示单线程1万次计算的总时间,单位 ms。
| SchemaType | 加密 | 密文+密文 | 密文+明文 | 密文*明文 | 解密 |
| OU | 278 | 18.1 | 52.5 | 529 | 2458 |
| ZPaillier | 8141 | 70.9 | 192 | 1960 | 86984 |
| FPaillier | 151187 | 230 | 150529 | 1692 | 150580 |
验证GPaillier性能
https://github.com/secretflow/heu/tree/main/heu/library/algorithms/paillier_gpu
使用须知
- 该算法为 Paillier 算法的实验性实现,请勿用于生产环境
- 该算法的性能不佳,请改进此算法
- 该算法底层依赖 Nvidia CGBN 第三方库,CGBN 属于 NVlabs 的产品,目前已经停止维护,请慎用
Key size = 2048,schema = gpaillier,矩阵(10000,1)的各项性能,单位ms。
| SchemaType | 加密 | 密文+密文 | 密文+明文 | 密文*明文 | 解密 |
| GPaillier | 2647 | 75 | 124 | 124 | 2504 |
GPaillier和ZPaillier性能对比

可修改 heu/library/benchmark/np_bench.cc,调整测试数据大小和秘钥长度。
GPU Docker环境
docker pull 镜像
# https://hub.docker.com/r/secretflow/heu-ci/tags
docker pull dockerpull.com/secretflow/heu-ci:latest启动docker镜像-gpu
docker run --gpus all --runtime=nvidia -e NVIDIA_VISIBLE_DEVICES=all -itd secretflow/heu-ci /bin/bash安装对应版本cuda
# https://developer.nvidia.com/cuda-12-4-0-download-archive?target_os=Linux&target_arch=x86_64&Distribution=Ubuntu&target_version=22.04&target_type=runfile_local
wget https://developer.download.nvidia.com/compute/cuda/12.4.0/local_installers/cuda_12.4.0_550.54.14_linux.run
sudo sh cuda_12.4.0_550.54.14_linux.run
获取heu代码
wget https://github.com/secretflow/heu/archive/refs/tags/v0.5.1b0.tar.gz代码编译打包
ENABLE_GPU= python setup.py bdist_wheel编译打包失败:
eigen拉取超时失败,手动下载并配置本地http服务,配置下载地址。vim /home/admin/heu-0.5.1b0/third_party/bazel_cpp/repositories.bzldef _com_github_eigenteam_eigen():EIGEN_COMMIT = "66e8f38891841bf88ee976a316c0c78a52f0cee5"EIGEN_SHA256 = "01fcd68409c038bbcfd16394274c2bf71e2bb6dda89a2319e23fc59a2da17210"maybe(http_archive,name = "com_github_eigenteam_eigen",sha256 = EIGEN_SHA256,build_file = "@com_alipay_sf_heu//third_party/bazel_cpp:eigen.BUILD",strip_prefix = "eigen-{commit}".format(commit = EIGEN_COMMIT),urls = ["http://localhost:8080/eigen-66e8f38891841bf88ee976a316c0c78a52f0cee5.tar.gz,#"https://gitlab.com/libeigen/eigen/-/archive/{commit}/eigen-{commit}.tar.gz".format(# commit = EIGEN_COMMIT,#),],)修改后编译成功:
sf_heu-0.5.1b0-cp310-cp310-manylinux2014_x86_64.whl
GPaillier仅支持2048
>> YACL_ENFORCE(key_size == 2048, "GPU Paillier only supports 2048 key_size now");

GPaillier 运行性能测试
bazel run -c opt heu/library/benchmark:np --config=gpu -- --schema=gpaillier

相关文章:

【隐私计算】隐语HEU同态加密算法解读
HEU: 一个高性能的同态加密算法库,提供了多种 PHE 算法, 包括ZPaillier、FPaillier、IPCL、Damgard Jurik、DGK、OU、EC ElGamal 以及基于FPGA和GPU硬件加速版本的Paillier版本。 本文我们会基于GPU运行HEU Docker容器,编译打包GPaillier并测…...

用C#实现互斥操作
1、传统的lock lock简单易用,适合大多数场景,但在高竞争用情况下可能会导致线程阻塞; Object obj new object(); void method1(){lock (obj){// 进行互斥操作}}2、SpinLock SpinLock在低延迟情况下更有效,因为SpinLock会在忙等…...

【黑马点评优化】之使用Caffeine+Redis实现应用级二层缓存
【黑马点评优化】之使用CaffeineRedis实现应用级二层缓存 1 缓存雪崩定义及解决方案2 为什么要使用多级缓存3 RedisCaffeine实现应用层二级缓存原理4 利用CaffeineRedis解决Redis突然宕机导致的缓存雪崩问题4.1 pom.xml文件引入相关依赖4.2 本地缓存配置类4.3 修改ShopServiceI…...

CEEMDAN +组合预测模型(BiLSTM-Attention + ARIMA)
往期精彩内容: 时序预测:LSTM、ARIMA、Holt-Winters、SARIMA模型的分析与比较 全是干货 | 数据集、学习资料、建模资源分享! EMD、EEMD、FEEMD、CEEMD、CEEMDAN的区别、原理和Python实现(一)EMD-CSDN博客 EMD、EEM…...

2.1.ReactOS系统中断描述符的格式KIDTENTRY结构体
2.1.ReactOS系统中断描述符的格式KIDTENTRY结构体 2.1.ReactOS系统中断描述符的格式KIDTENTRY结构体 文章目录 2.1.ReactOS系统中断描述符的格式KIDTENTRY结构体KIDTENTRY KIDTENTRY 数据结构KIDTENTRY定义了CPU对中断描述符的格式 // // …...

三、ElementPlus下拉搜索加弹窗组件的封装
近期产品提出了一个需求,要求一个form的表单里面的一个组件既可以下拉模糊搜索,又可以弹窗搜索,我就为这个封装了一个组件,下面看效果图。 效果大家看到了,下面就看组件封装和实现方法 第一步,组件封装&…...

androidStudio编译导致的同名.so文件冲突问题解决
files found with path lib/arm64-v8a/libserial_port.so from inputs: ...\build\intermediates\library_jni\debug\jni\arm64-v8a\libserial_port.so C:\Users\...\.gradle\caches\transforms-3\...\jni\arm64-v8a\XXX.so 解决方式如下: 1.将gradle缓存文件删…...

大学新生编程入门指南:如何选择编程语言与制定学习计划
大学新生编程入门指南:如何选择编程语言与制定学习计划 编程已成为当代大学生的必备技能,尤其是在信息技术高速发展的今天,编程能力不仅能帮助你在课堂学习中脱颖而出,更能为未来职业生涯打下坚实的基础。然而,面对如…...

SpringAI快速上手
一、导入依赖 镜像(导入maven依赖) <repositories><repository><id>spring-snapshots</id><name>Spring Snapshots</name><url>https://repo.spring.io/snapshot</url><releases><enabled>…...

07 django管理系统 - 部门管理 - 搜索部门
在dept_list.html中,添加搜索框 <div class"container-fluid"><div style"margin-bottom: 10px" class"clearfix"><div class"panel panel-default"><!-- Default panel contents --><div clas…...

数据操作学习
1.导入torch。虽然被称为PyTorch,但应导入torch而不是pytorch import torch 2.张量表示一个数值组成的数组,这个数组可能有多个维度 xtorch.arange(12)x 3.通过张量的shape属性来访问张量的形状和张量中元素的总数 x.shape x.numel() 4.要改变张量的形…...

什么是网络代理
了解网络代理 网络代理是一种特殊的网络服务,它允许一个网络终端(通常指客户端)通过这个服务与另一个网络终端(通常指服务器)进行非直接的连接。网络代理服务器位于发送主机和接收主机之间,接收网络请求&a…...

安防监控摄像头图传模组,1公里WiFi无线传输方案,监控新科技
在数字化浪潮汹涌的今天,安防监控领域也迎来了技术革新的春风。今天,我们就来聊聊这一领域的产品——摄像头图传模组,以及它如何借助飞睿智能1公里WiFi无线传输技术,为安防监控带来未有的便利与高效。 一、安防监控的新篇章 随着…...

问:JVM中GC类型有哪些?触发条件有哪些?区别是啥?
在Java虚拟机(JVM)中,垃圾收集(GC)是自动管理内存的关键机制。GC负责识别并回收那些不再被程序使用的对象,以释放内存空间。根据回收的区域和策略的不同,JVM中的GC可以分为多种类型。 一、GC的…...

【操作系统的使用】Linux 输入输出重定向:掌握控制台的高级用法
文章目录 Linux 输入输出重定向:掌握控制台的高级用法输出重定向将命令输出保存到文件将命令输出追加到文件 输入重定向从文件读取输入 管道操作将多个命令的输出链接起来 错误重定向将错误信息保存到文件同时重定向输出和错误信息 Linux 输入输出重定向:…...

无线通信中的四个关键概念:OFDM、多径效应、CSI和信道均衡
无线通信中的四个关键概念:OFDM、多径效应、CSI和信道均衡 无线通信技术在现代通信系统中发挥着至关重要的作用。无论是日常的手机通信,还是复杂的物联网应用,理解无线信道的特性和优化信号传输的技术是关键。在本文中,我们将介绍…...
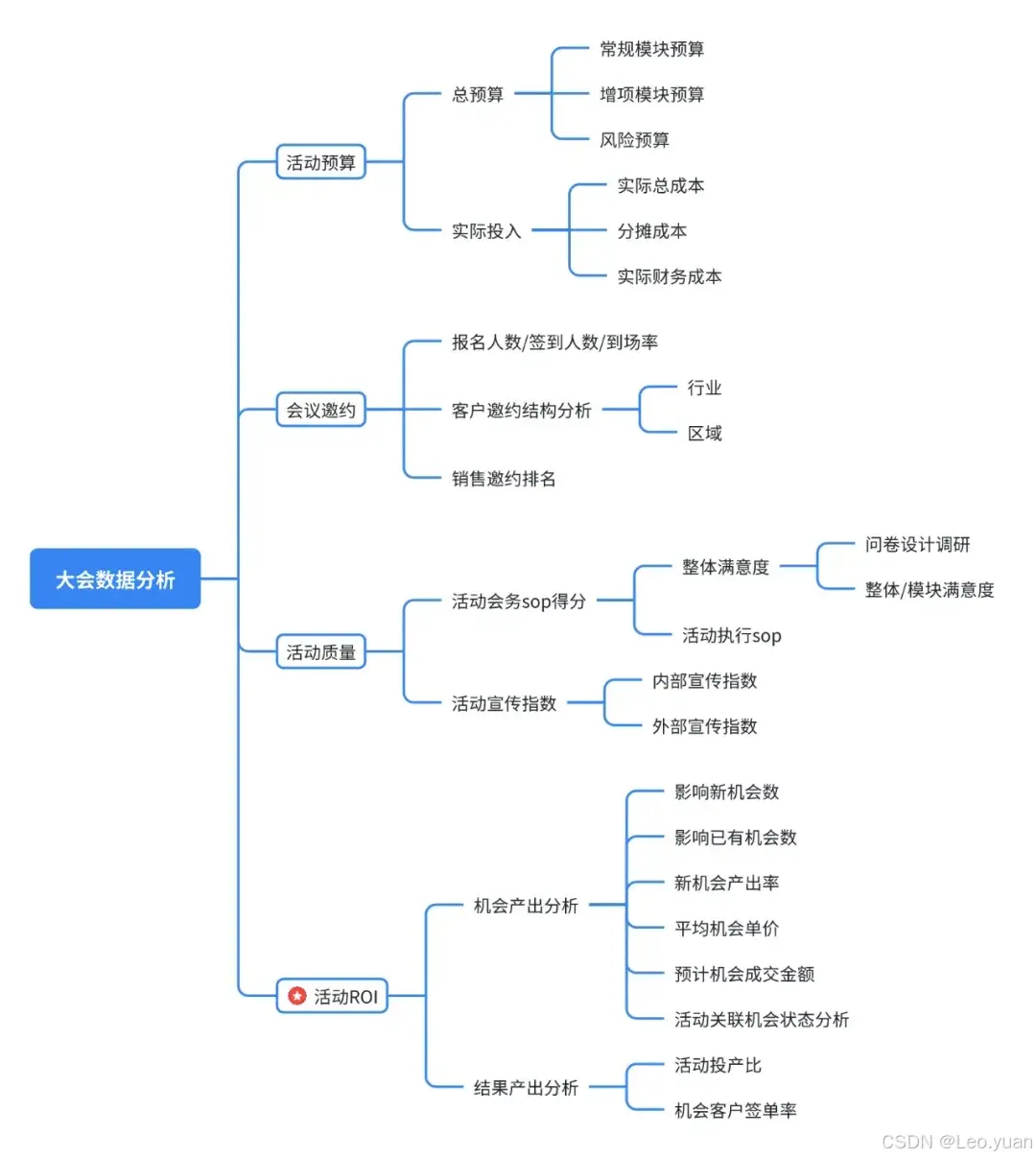
如何高效规划千人大会?数字化会议管理的实战经验分享!建议收藏!
在当今快节奏的商业环境中,大型会议不仅是企业展示自身实力、促进交流合作的重要平台,更是推动行业发展、分享创新思维的关键活动。然而,随着参会人数的增加,如何高效规划并管理一场千人大会,成为了组织者面临的巨大挑…...
)
mysql指令笔记(基本)
一、数据库操作 创建数据库:CREATE DATABASE database_name;选择数据库:USE database_name;删除数据库:DROP DATABASE database_name; 二、表操作 创建表:CREATE TABLE table_name (column1 datatype constraint, column2 datat…...

web前端-----html5----用户注册
以改图为例 <!DOCTYPE html> <html lang"en"> <head> <meta charset"UTF-8"> <meta name"viewport" content"widthdevice-width, initial-scale1.0"> <title>用户注册</title> </hea…...

bug的定义和测试
一、软件测试的生命周期 软件测试的⽣命周期是指测试流程,这个流程是按照⼀定顺序执⾏的⼀系列特定的步骤,去保证产品 质量符合需求。在软件测试⽣命周期流程中,每个活动都按照计划的系统的执⾏。每个阶段有不同的 ⽬标和交付产物 需求分析…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...
