动态规划17:123. 买卖股票的最佳时机 III
动态规划解题步骤:
1.确定状态表示:dp[i]是什么
2.确定状态转移方程:dp[i]等于什么
3.初始化:确保状态转移方程不越界
4.确定填表顺序:根据状态转移方程即可确定填表顺序
5.确定返回值
题目链接:123. 买卖股票的最佳时机 III - 力扣(LeetCode)

题解:
1.状态表示:
f[k][i]表示截止第i天,第i天为可买入状态的最大利润,且当前已交易k次
g[k][i]表示截止第i天,第i天为可卖出状态的最大利润,且当前已交易k次
2.状态转移方程:
f[k][i]=max(f[k][i-1],g[k-1][i-1]+prices[i])
g[k][i]=max(g[k][i-1],f[k][i-1]-prices[i])
3.初始化:初始化第一列为负无穷(-0x3f3f3f3f),另外 f[0][0]=0 g[0][0]=-prices[0];
注意:对于f表,其本应该初始化第一行和第一列,但是为了优化代码和g表保持一致,可以只初始化第一列,对于第一行的数据只需对其状态转移方程添加位置判断即可,对于不合法的位置其状态转移方程为f[k][i-1],合法位置的状态转移方程为max(f[k][i-1],g[k-1][i-1]+prices[i])
4.填表顺序:从上往下,从左往右,两个表一起填
5.返回值:返回第n-1天为可买入状态的最大利润(交易次数可能为0、1、2)

class Solution {
public:const int INF=0x3f3f3f3f;int maxProfit(vector<int>& prices) {//f[k][i]表示截止第i天,第i天为可买入状态的最大利润,且当前已交易k次//g[k][i]表示截止第i天,第i天为可卖出状态的最大利润,且当前已交易k次//第i天为可买入状态,则前一天有两种情况:前一天为可买入状态,交易次数相同,今天什么也没做;// 前一天为可卖出状态,交易次数少1,今天卖出了股票//f[k][i]=max(f[k][i-1],g[k-1][i-1]+prices[i])//第i天为可卖出状态,则前一天有两种情况:前一天为可卖出状态,交易次数相同,今天什么也没做// 前一天为可买入状态,交易次数相同,今天买了股票//g[k][i]=max(g[k][i-1],f[k][i-1]-prices[i])size_t n=prices.size();//处理边界条件if(n==1) return 0;//创建dp表vector<vector<int>> f(3,vector<int>(n,-INF));vector<vector<int>> g(3,vector<int>(n,-INF));//初始化(创建dp表时已初始化一部分,相当于初始化了第一列)f[0][0]=0;g[0][0]=-prices[0];//填表for(int k=0;k<=2;++k){for(int i=1;i<n;++i){if(k-1>=0) f[k][i]=max(f[k][i-1],g[k-1][i-1]+prices[i]);else f[k][i]=f[k][i-1];g[k][i]=max(g[k][i-1],f[k][i-1]-prices[i]);}}//返回值return max(f[0][n-1],max(f[1][n-1],f[2][n-1]));}
};相关文章:

动态规划17:123. 买卖股票的最佳时机 III
动态规划解题步骤: 1.确定状态表示:dp[i]是什么 2.确定状态转移方程:dp[i]等于什么 3.初始化:确保状态转移方程不越界 4.确定填表顺序:根据状态转移方程即可确定填表顺序 5.确定返回值 题目链接:123.…...

华为OD机试真题---预定酒店
华为OD机试真题中的“预定酒店”题目是一道典型的算法题,主要考察的是如何在给定的酒店价格数组中找到最接近心理价位的k个酒店,并按价格从低到高输出。以下是对该题目的详细解析: 一、题目描述 放暑假了,小明决定到某旅游景点游…...

力扣242.有效的字母异位词
题目链接:242. 有效的字母异位词 - 力扣(LeetCode) 给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的 字母异位词。 示例 1: 输入: s "anagram", t "nagaram"输出: true 示例 2: 输入: s &q…...

Android IP路由策略和防火墙
Android IP路由策略和防火墙 Platform: RK3368 OS: Android 6.0 Kernel: 3.10.0 文章目录 Android IP路由策略和防火墙ip route, ip rule, iptables简介ip routeip ruleiptables Android路由策略Android路由策略优先级命令查看当前路由策略 Android路由表命令查看路由表命令…...

MySQL insert ... select 语句锁表导致数据写不进去
问题现象 调用后台接口向表 t1 insert 写入数据时一直等待直到超时,猜测表 t1 被其它事务加锁了没有释放。 问题分析 在发生死锁时,通过执行下面命令查看事务和锁信息: select * from information_schema.INNODB_TRX 用来查看正在运行的事…...

Android摄像头Camera2和Camera1的一些总结
Android 系统对摄像头的同时使用有限制,不能同时使用摄像头进行预览或者录制音视频。 例如:界面上有两个SurfaceView, 这两个SurfaceView不能同时预览或者录制音视频,只能有一个正常工作(一个SurfaceView预览前置摄像头ÿ…...

【Linux 从基础到进阶】Linux中的用户认证与授权
Linux中的用户认证与授权 1. 引言 在Linux系统中,**用户认证(authentication)和授权(authorization)**是两个核心的安全机制,用来控制系统资源的访问和管理用户操作权限。用户认证确保登录的用户是合法的…...

用户界面设计:视觉美学与交互逻辑的融合
1、什么是用户界面 用户界面(UI)是人与机器之间沟通的桥梁,同时也是用户体验(UX)的重要组成部分。用户界面设计包括两个核心要素:视觉设计(即产品的外观和感觉)和交互设计ÿ…...

ZK集群搭建:详细步骤与注意事项
在大数据和分布式系统日益重要的今天,ZooKeeper(简称ZK)作为一种分布式协调服务,扮演着举足轻重的角色。它主要用于管理大型分布式系统中的配置信息、命名、同步等。下面将详细介绍如何搭建一个ZooKeeper集群,帮助大家…...

如何将csdn文章导出为pdf
前言 在csdn上浏览文章的时候我发现有的文章支持pdf导出,但是有的文章不支持pdf导出,为了解决能将csdn上所有文章都能以pdf格式导出遂作此文。 正文 先上代码: (function(){use strict;var contentBox $("div.article_content")…...

【艾思科蓝】Imagen:重塑图像生成领域的革命性突破
【连续七届已快稳ei检索】第八届电子信息技术与计算机工程国际学术会议(EITCE 2024)_艾思科蓝_学术一站式服务平台 更多学术会议请看 学术会议-学术交流征稿-学术会议在线-艾思科蓝 目录 引言 一、Imagen模型的技术原理 1. 模型概述 2. 工作流程 …...

java类和对象(下): 封装 static成员 内部类
前言: 在前期的知识点中,我们学习了java中this函数的使用和相关的概念。这期我们将介绍封装的概念,以及常见内部类的使用,让我们开车吧!!!! 本期目录: 6. 封装 7. st…...

外包干了3周,技术退步太明显了。。。。。
先说一下自己的情况,大专生,21年通过校招进入武汉某软件公司,干了差不多3个星期的功能测试,那年国庆,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落!而我才在一个外包企业干了3周的功…...

VIVO算法题——数位之积
记录算法究极无敌菜菜菜鸟的垃圾思维 题目: 现给定任意正整数 n,请寻找并输出最小的正整数 m(m>9),使得 m 的各位(个位、十位、百位 … …)之乘积等于n,若不存在则输出 -1。 菜鸟…...
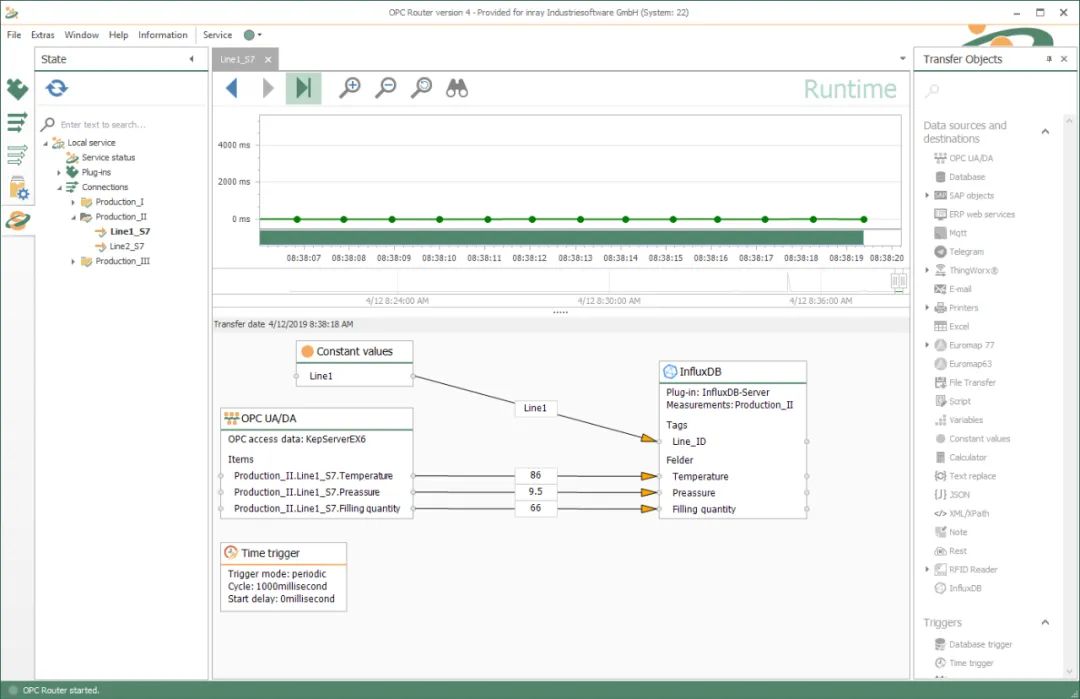
OPC Router快速打通设备层与influxDB数据通讯
随着时代演化,数据量呈几何倍数增加的情况下出现了时序数据库。时序数据库是基于时间进行存储的数据库,每一条数据中都有一个时间戳,这种数据库特别适合存储那些随着时间变化的数据,通过一些工具处理后,能够分析出数据…...

鸿蒙开发 四十四 ArkTs BuilderParam传递UI(二)
子组件多个BuilderParam,必须通过参数的方式传入,如果界面中有多个界面需要传递,可以定义多个尾随闭包,如图: 在自定义组件中调用: 在使用时候调用是作为参数传递给自定义的组件,参数是界面&…...

同期数分析-留存率
目录 同期数分析 加载数据 单月实现 统计每个月的订单量 求2月份的订单量和用户数量 求2月之前的历史订单量 筛选出2023年2月的新增的用户数 计算2023年2月在后面的留存情况 完整的2023年2月份同期群结果 遍历合并和分析 引入月份列表 遍历 调整成留存率的形式 回…...

Java前后端交互:构建现代Web应用
在现代Web应用开发中,前后端分离是一种常见的架构模式。后端通常负责数据处理和业务逻辑,而前端则负责用户界面和用户体验。Java作为后端开发的强大语言,提供了多种方式与前端进行交互。本文将探讨Java后端与前端交互的几种主要方式ÿ…...

vue3中用axios请求怎么添加cookie
在 Vue 3 中使用 axios 发起请求时,可以通过配置 axios 的请求选项来携带 Cookies。具体来说,确保跨域请求时,设置 withCredentials: true,以便发送和接收 Cookies。 1. Axios 配置携带 Cookie 首先确保你在 axios 请求中设置了…...

informer学习笔记
一、informer讲解 infomer 要解决的三大问题: Attention计算的更快Decoder要一次性输出所有预测堆叠encoder也要更快 1. Attention 在长序列中,并非每一个位置的Attention都重要,对于每一个Q来说,只有一小部分的K与其有较强的…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...
