Python解力扣算法题4(基础)
# 1.求斐波那契数列下标为n的数 (从零开始)
# def fib(n):
# if n < 2:
# return n
#
# p, q, r = 0, 0, 1
# for i in range(2, n + 1):
# p, q = q, r
# r = p + q
#
# return r#2. 和谐数组是指一个数组里元素的最大值和最小值之间的差别 正好是 1 。
# 现在,给你一个整数数组 nums ,请你在所有可能的子序列中找到最长的和谐子序列的长度。
# 在这段代码中,Counter(nums)会返回一个字典,其中的键是数组中的数,值是这个数在数组中出现的次数。
# 然后,对于字典中的每个数,我们检查x + 1是否在字典中,如果在,那么就更新最长的和谐子序列的长度。
# def findLHS(nums):
# from collections import Counter
# count = Counter(nums)
# # print(count) Counter({2: 3, 3: 2, 1: 1, 5: 1, 7: 1})
# ans = 0
# for x in count:
# if x + 1 in count:
# ans = max(ans, count[x] + count[x+1])
# return ans
# print(findLHS([1,3,2,2,5,2,3,7]))# 3.假设有一个很长的花坛,一部分地块种植了花,另一部分却没有。可是,花不能种植在相邻的地块上,它们会争夺水源,两者都会死去。
# 给你一个整数数组 flowerbed 表示花坛,由若干 0 和 1 组成,其中 0 表示没种植花,1 表示种植了花。另有一个数 n ,能否在不打破种植规则的情况下种入 n 朵花?
# 能则返回 true ,不能则返回 false 。
# def canPlaceFlowers(flowerbed, n):
# # count用来检测当前种了几朵花
# count = 0
# flowerbed = [0] + flowerbed + [0]
# # len(flowerbed) - 1是为了后面遍历flowerbed[i + 1]防止越界
# for i in range(1, len(flowerbed) - 1):
# if flowerbed[i - 1] == 0 and flowerbed[i] == 0 and flowerbed[i + 1] == 0:
# flowerbed[i] = 1
# count += 1
# if count >= n:
# return True
# return False
# print(canPlaceFlowers([1,0,0,0,1],1))# 4.给你一个整型数组 nums ,在数组中找出由三个数组成的最大乘积,并输出这个乘积。
# 法1 超时
# def maximumProduct(nums):
# max=nums[0]*nums[1]*nums[2]
# for i in range(0,len(nums)):
# for j in range(i+1,len(nums)):
# for k in range(j+1,len(nums)):
# if nums[i]*nums[j]*nums[k]>max:
# max=nums[i]*nums[j]*nums[k]
# return max# 法2
# def maximumProduct(nums):
# nums.sort()
# # 两个最小的数和最大的数的乘积
# min_product = nums[0] * nums[1] * nums[-1]
# # 三个最大的数的乘积
# max_product = nums[-1] * nums[-2] * nums[-3]
# return max(min_product, max_product)
# print(maximumProduct([-1,-2,-3]))# 5.给你一个由 n 个元素组成的整数数组 nums 和一个整数 k 。
# 请你找出平均数最大且 长度为 k 的连续子数组,并输出该最大平均数。
# 任何误差小于 10-5 的答案都将被视为正确答案。
# def findMaxAverage(nums, k):
# maxtotal = total = sum(nums[:k])
# n = len(nums)
# for i in range(k, n):
# total = total - nums[i - k] + nums[i]
# maxtotal = max(total, maxtotal)
# return maxtotal / k
# print(findMaxAverage([1,12,-5,-6,50,3],4))# 6.集合 s 包含从 1 到 n 的整数。不幸的是,因为数据错误,导致集合里面某一个数字复制了成了集合里面的另外一个数字的值,导致集合 丢失了一个数字 并且 有一个数字重复 。
# 给定一个数组 nums 代表了集合 S 发生错误后的结果。
# 请你找出重复出现的整数,再找到丢失的整数,将它们以数组的形式返回。
# def findErrorNums(nums):
# total = sum(range(1, len(nums) + 1))
# num = total - sum(set(nums))
# diff = total - sum(nums)
# 我(错误的)离正确的(3)少了一个,所以我(错误的)是2
# return [num - diff, num]# 7.给定一个字符串 s ,你需要反转字符串中每个单词的字符顺序,同时仍保留空格和单词的初始顺序。
# def reverseWords(s):
# s=s.split(" ")
# for i in range(len(s)):
# s[i]=s[i][::-1]
# # 用空格连接s中的每个元素并返回连接后的字符串
# return " ".join(s)
#
# print(reverseWords("Let's take LeetCode contest"))# 8.给定长度为 2n 的整数数组 nums ,你的任务是将这些数分成 n 对, 例如 (a1, b1), (a2, b2), ..., (an, bn) ,使得从 1 到 n 的 min(ai, bi) 总和最大。
# 返回该 最大总和 。
# 容易想到答案就是将列表排序后,每隔一个取一个数,这些数相加就是满足题意的最大总和
# def arrayPairSum(nums):
# nums.sort()
# return sum(nums[::2])
# print(arrayPairSum([6,2,6,5,1,2]))# 9.在二维平面上,有一个机器人从原点 (0, 0) 开始。给出它的移动顺序,判断这个机器人在完成移动后是否在 (0, 0) 处结束。
# 移动顺序由字符串 moves 表示。字符 move[i] 表示其第 i 次移动。机器人的有效动作有 R(右),L(左),U(上)和 D(下)。
# 如果机器人在完成所有动作后返回原点,则返回 true。否则,返回 false。
# def judgeCircle(moves):
# num = 0
# num1 = 0
# for i in moves:
# if i == "U":
# num += 1
# if i == "D":
# num -= 1
# if i == "R":
# num1 += 2
# if i == "L":
# num1 -= 2
# return num == 0 and num1 == 0#print(judgeCircle("UDDUURLRLLRRUDUDLLRLURLRLRLUUDLULRULRLDDDUDDDDLRRDDRDRLRLURRLLRUDURULULRDRDLURLUDRRLRLDDLUUULUDUUUUL"))# 10.给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度
# def findLengthOfLCIS(nums):
# count=1
# max=0
# if len(nums)==1:
# return 1
# for i in range(len(nums)-1):
# if nums[i+1]>nums[i]:
# count+=1
# else:
# count=1
# if count>max:
# max=count
# return max
#
# print(findLengthOfLCIS([1,3,5,4,7]))# 11.给你一个字符串 s,最多 可以从中删除一个字符。
# def validPalindrome(self, s):
# isPalindrome = lambda x : x == x[::-1]
# left, right = 0, len(s) - 1
# while left <= right:
# if s[left] == s[right]:
# left += 1
# right -= 1
# else:
# return isPalindrome(s[left + 1 : right + 1]) or isPalindrome(s[left: right])
# return True
# print(validPalindrome("abca"))# 12.你现在是一场采用特殊赛制棒球比赛的记录员。这场比赛由若干回合组成,过去几回合的得分可能会影响以后几回合的得分。
# 比赛开始时,记录是空白的。你会得到一个记录操作的字符串列表 ops,其中 ops[i] 是你需要记录的第 i 项操作,ops 遵循下述规则:
# 整数 x - 表示本回合新获得分数 x
# "+" - 表示本回合新获得的得分是前两次得分的总和。题目数据保证记录此操作时前面总是存在两个有效的分数。
# "D" - 表示本回合新获得的得分是前一次得分的两倍。题目数据保证记录此操作时前面总是存在一个有效的分数。
# "C" - 表示前一次得分无效,将其从记录中移除。题目数据保证记录此操作时前面总是存在一个有效的分数。
# 请你返回记录中所有得分的总和。
# def calPoints(ops):
# ans = 0
# points = []
# for op in ops:
# if op == '+':
# pt = points[-1] + points[-2]
# elif op == 'D':
# pt = points[-1] * 2
# elif op == 'C':
# ans -= points.pop()
# continue
# else:
# pt = int(op)
# ans += pt
# points.append(pt)
# return ans
# print(calPoints(["5","2","C","D","+"]))# 13.给你一个整数数组 nums ,请计算数组的 中心下标 。
# 数组 中心下标 是数组的一个下标,其左侧所有元素相加的和等于右侧所有元素相加的和。
# 如果中心下标位于数组最左端,那么左侧数之和视为 0 ,因为在下标的左侧不存在元素。这一点对于中心下标位于数组最右端同样适用。
# 如果数组有多个中心下标,应该返回 最靠近左边 的那一个。如果数组不存在中心下标,返回 -1 。# 这题要求某个区间的元素之和,立马想到 preSum 这个方法。
# 它的计算方法是从左向右遍历数组,当遍历到数组的 i 位置时,preSum表示 i 位置左边的元素之和。
# 我们提前计算出所有元素之和 sums_,那么 sums_ - preSum - nums[i] 就是 i 位置右边元素之和。
# 如果 preSum == sums_ - preSum - nums[i],那么 i 就是满足题目含义的「中心索引」位置。
# 如果遍历完数组,都没有发现满足题意的「中心索引」,那么返回 -1 .# def pivotIndex(nums):
# N = len(nums)
# sums_ = sum(nums)
# preSum = 0
# for i in range(N):
# if preSum == sums_ - preSum - nums[i]:
# return i
# preSum += nums[i]
# return -1
#
# print(pivotIndex([1, 7, 3, 6, 5, 6]))# 14.自除数 是指可以被它包含的每一位数整除的数。
# 例如,128 是一个 自除数 ,因为 128 % 1 == 0,128 % 2 == 0,128 % 8 == 0。
# 自除数 不允许包含 0 。
# 给定两个整数 left 和 right ,返回一个列表,列表的元素是范围 [left, right](包括两个端点)内所有的 自除数 。
# def selfDividingNumbers(left, right):
# list1=[]
# for i in range(left,right+1):
# if i==0:
# continue
# digits = []
# list2=[int(j) for j in str(i)]
# n=len(list2)
# count=0
# for j in list2:
# if j==0:
# continue
# if i % j==0:
# count+=1
# if count==n:
# list1.append(i)
# return list1
#
# print(selfDividingNumbers(1,22))# 15.Alice 有 n 枚糖,其中第 i 枚糖的类型为 candyType[i] 。Alice 注意到她的体重正在增长,所以前去拜访了一位医生。
# 医生建议 Alice 要少摄入糖分,只吃掉她所有糖的 n / 2 即可(n 是一个偶数)。Alice 非常喜欢这些糖,她想要在遵循医生建议的情况下,尽可能吃到最多不同种类的糖。
# 给你一个长度为 n 的整数数组 candyType ,返回: Alice 在仅吃掉 n / 2 枚糖的情况下,可以吃到糖的 最多 种类数。
# def distributeCandies(candyType):
# num=len(candyType)
# num=num//2
# candy=set(candyType)
# if len(candy)==num:
# return num
# elif len(candy)>num:
# return num
# else:
# return len(candy)
#
#
# print(distributeCandies([6,6,6,6]))
相关文章:
)
Python解力扣算法题4(基础)
# 1.求斐波那契数列下标为n的数 (从零开始) # def fib(n): # if n < 2: # return n # # p, q, r 0, 0, 1 # for i in range(2, n 1): # p, q q, r # r p q # # return r#2. 和谐数组是指一个数组里元素…...

鸿蒙NEXT开发-网络管理(基于最新api12稳定版)
注意:博主有个鸿蒙专栏,里面从上到下有关于鸿蒙next的教学文档,大家感兴趣可以学习下 如果大家觉得博主文章写的好的话,可以点下关注,博主会一直更新鸿蒙next相关知识 专栏地址: https://blog.csdn.net/qq_56760790/…...

【LeetCode每日一题】——1413.逐步求和得到正数的最小值
文章目录 一【题目类别】二【题目难度】三【题目编号】四【题目描述】五【题目示例】六【题目提示】七【解题思路】八【时间频度】九【代码实现】十【提交结果】 一【题目类别】 前缀和 二【题目难度】 简单 三【题目编号】 1413.逐步求和得到正数的最小值 四【题目描述】…...

音频分割:长语音音频 分割为 短语音音频 - python 实现
在做语音任务时,有是会用到的语音音频是长音频,这就需要我们将长音频分割为短音频。 该示例将声音的音量和静默时间结合作为语音的分割条件。 使用音量和静默时间结合的分割条件,能够比较好的进行自然断句,不会话语没有说完就切断…...

【Echarts动态排序图,series使用背景色更新动画,背景底色不同步跟随柱子动画】大家有没有解决方案
echarts动态排序图背景色动画不同步 echarts试一试 series下面添加了showBackground属性,动画时底色背景不同步跟随柱图 showBackground: true, backgroundStyle: {borderRadius: 9,color: RGB(255,199,91, 0.2) }const data []; for (let i 0; i < 5; i) {d…...

FLINK SQL 元数据持久化扩展
Flink SQL元数据持久化扩展是一个复杂但重要的过程,它允许Flink作业在重启或失败后能够恢复状态,从而确保数据处理的连续性和准确性。以下是对Flink SQL元数据持久化扩展的详细分析: 一、元数据持久化的重要性 在Flink中,元数据…...

MySQL【知识改变命运】04
复习: 1:CURD 1.1Create (创建) 语法: insert [into] 表名 [column[,column]] valuse(value_list)[,vaule_list]... value_list:value,[value]...创建一个实例表: 1.1.1单⾏数据全列插⼊ values_l…...

AD9680(adc直采芯片)使用说明
写这篇文章之前我是没有使用过AD9680的芯片,但是使用过GMS011芯片(是国内24S)下的公司出来的芯片,寄存器和管脚全对标。 在这里我就大概说一下芯片的说用方法 一、硬件设计 该芯片支持双通道射频直采 支持协议JESD204B 14位 采样…...

无人机之位置信息计算篇
一、主要导航技术 卫星导航 全球定位系统(GPS):无人机上装有专门的接收器,用于捕获GPS系统发射的无线电信号。当无人机接收到来自至少四颗卫星的信号时,通过计算信号抵达时间的微小差异,即可运用三角定位…...

安卓cpu知识
背景 目前的cpu都是多核的,为了有更好的能效,每个核的频率从低往高不等。市面上,大家根据频率不同,都叫大小核。既然分了大小核,那么多核心,就要有不同的cpu调度策略。所以cpu上的所有核,又会根…...

图书管理新纪元:Spring Boot进销存系统
1系统概述 1.1 研究背景 随着计算机技术的发展以及计算机网络的逐渐普及,互联网成为人们查找信息的重要场所,二十一世纪是信息的时代,所以信息的管理显得特别重要。因此,使用计算机来管理图书进销存管理系统的相关信息成为必然。开…...

Application protocol
5 应用协议 在 TS 31.101 [11] 的对应条款中所述的要求适用于 USIM 应用。 在执行后续章节“USIM 安全相关程序”和“订阅相关程序”中的程序之前,必须执行“USIM 管理程序”中列出的程序。“USIM 安全相关程序”中列出的程序是强制性的。“订阅相关程序”中列出的程…...
金融信用评分卡建模项目:AI辅助
最近我一直忙着开发一个信用评分卡建模工具,所以没有时间更新示例或动态。今天,我很高兴地跟大家分享,这个工具的基本框架已经完成了,并且探索性的将大语言模型(AI)整合了进去。目前ai在工具中扮演智能助手…...

java对接GPT 快速入门
统一对接GPT服务的Java说明 当前,OpenAI等GPT服务厂商主要提供HTTP接口,这使得大部分Java开发者在接入GPT时缺乏标准化的方法。 为解决这一问题,Spring团队推出了Spring AI ,它提供了统一且标准化的接口来对接不同的AI服务提供商…...
微信小程序引入组件教程
1、安装 node.js 下载网址:https://nodejs.org 2.通过 npm 安装 npm init -y npm i vant/weapp -S --production 3、修改 app.json 将 app.json 中的 “style”: “v2” 去除 4、修改 project.config.json 关于修改 project.config.json 的详细内容&#x…...

STM32—SPI通信外设
1.SPI外设简介 STM32内部集成了硬件SPI收发电路,可以由硬件自动执行时钟生成、数据收发等功能,减轻CPU的负担可配置8位/16位数据帧、高位先行/低位先行时钟频率:fpclk/(2,4,8,16,32,64,128,256)支持多主机模型、主或从操作可精简为半双工/单…...

Ubuntu:用户不在sudoers文件中
1、问题 执行sudo xxx命令时,显示: user 不在sudoers文件中 需要查看系统版本进入恢复模式修复。 2、重启进入恢复模式 查看系统命令:uname -r 可能显示为:6.8.0-45-generic 重启Ubuntu系统,在开机时按ESC进入模…...
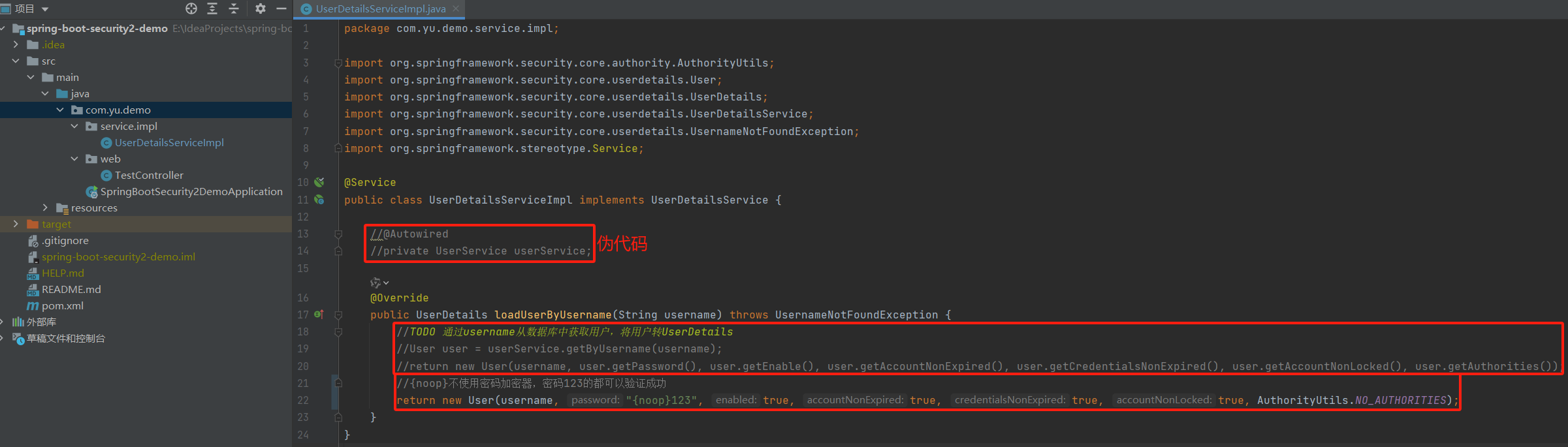
五、Spring Boot集成Spring Security之认证流程2
一、Spring Boot集成Spring Security专栏 一、Spring Boot集成Spring Security之自动装配 二、Spring Boot集成Spring Security之实现原理 三、Spring Boot集成Spring Security之过滤器链详解 四、Spring Boot集成Spring Security之认证流程 五、Spring Boot集成Spring Se…...
接口测试(全)
🍅 点击文末小卡片,免费获取软件测试全套资料,资料在手,涨薪更快 1、什么是接口测试 顾名思义,接口测试是对系统或组件之间的接口进行测试,主要是校验数据的交换,传递和控制管理过程࿰…...

【学习】word保存图片
word中有想保存的照片 直接右键另存为的话,文件总是不清晰,截屏的话,好像也欠妥。 怎么办? 可以另存为 网页 .html 可以得到: 原图就放到了文件夹里面...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

Python常用模块:time、os、shutil与flask初探
一、Flask初探 & PyCharm终端配置 目的: 快速搭建小型Web服务器以提供数据。 工具: 第三方Web框架 Flask (需 pip install flask 安装)。 安装 Flask: 建议: 使用 PyCharm 内置的 Terminal (模拟命令行) 进行安装,避免频繁切换。 PyCharm Terminal 配置建议: 打开 Py…...
