字节青训营入营考核部分题解
题库链接:https://juejin.cn/problemset?utm_source=school&utm_medium=youthcamp&utm_campaign=examine
1. 计算从x到y的最小步数
问题描述
AB 实验同学每天都很苦恼如何可以更好地进行 AB 实验,每一步的流程很重要,我们目标为了缩短所需的步数。
我们假设每一步对应到每一个位置。从一个整数位置 x 走到另外一个整数位置 y,每一步的长度是正整数,每步的值等于上一步的值 -1, +0,+1。求 x 到 y 最少走几步。并且第一步必须是 1,最后一步必须是 1,从 x 到 y 最少需要多少步。
样例说明
- 整数位置
x为12,另外一个整数位置y为6,我们需要从x走到y,最小的步数为:1,2,2,1,所以我们需要走4步。 - 整数位置
x为34,另外一个整数位置y为45,我们需要从x走到y,最小的步数为:1,2,3,2,2,1,所以我们需要走6步。 - 整数位置
x为50,另外一个整数位置y为30,我们需要从x走到y,最小的步数为:1,2,3,4,4,3,2,1,所以我们需要走8步。
输入格式
输入包含 2 个整数 x,y。(0<=x<=y<2^31)
输出格式
对于每一组数据,输出一行,仅包含一个整数,从 x 到 y 所需最小步数。
输入样例
12 6
34 45
50 30
输出样例
4
6
8
解题思路
- 从x到y的距离为
s := abs(x-y) - 由于每次的步数只能是上次基础上的+1、-1或0。所以,步数的过程由三部分组成:
- 1~n项和:
n*(n+1)/2 - 前1~n-1项和:
n*(n-1)/2 i个n- 0个或1个1~n之间的数
x
- 1~n项和:
- 整理为公式:
n^2 = s - i*n - x ans = 2*n-1+i+(0|1)
代码
func solution1(xPosition int, yPosition int) int {s := int(math.Abs(float64(yPosition - xPosition)))n := math.Sqrt(float64(s))ans := 2*int(n) - 1// 如果s不为完全平方数if n > float64(int(n)) {res := s - int(n)*int(n)if res%int(n) == 0 {ans += res / int(n)} else {ans += res/int(n) + 1}return ans} else {return ans}
}
2. 找出单独的数
问题描述
有一堆数字,除了一个数字,其它的数字都是成对出现。班上的每个同学拿一个数字,正好将这些数字全部拿完,问如何快速找到拿了单独数字的同学?
输入格式
- 空格分隔输入所有的数字
输出格式
- 单独的那个数字
输入样例(1)
1 1 2 2 3 3 4 5 5
输出样例(1)
4
输入样例(2)
0 1 0 1 2
输出样例(2)
2
解题思路
- 序列中只有一个数是单独的,其余两两配对。
- 考虑异或运算的恒等律和归零率。任何数与自身异或,结果为0;任何书与0异或,结果为其本身。
代码
func solution4(inp []int) int {// Edit your code hereans := 0for _, v := range inp {ans ^= v}return ans
}
3. 字符串最短循环子串
问题描述
- 输入一个字符串,判断其是否完全循环,若是循环的,输出最短的循环子串,否则输出空
"" - 如输入
abababab,输出ab;输入ab则输出""
输入格式
- 合法字符串 如
abcabcabcabcaaa
输出格式
- 最短的循环子串
"abc""a"
输入样例
"abcabcabcabc"
输出样例
"abc"
数据范围
测试数据集
解题思路
- tag为
简单题,应该不是考kmp算法吧,直接双for暴力。 - 外层循环遍历模板串,若原
len(inp)%len(s) != 0则跳过此串。 - 内层循环遍历原串,对模板串进行匹配,若匹配失败则退出循环,考虑下一个模板串。
代码
func solution2(inp string) string {if len(inp) < 2 {return ""}for i := 0; i < len(inp); i++ {s := inp[:i+1]if len(inp)%len(s) != 0 {continue}flag := falsefor j := 0; j < len(inp)-len(s); j += len(s) {if s != inp[j:j+len(s)] {flag = truebreak}}if flag {continue}return s}return ""
}
4. 找出最长神奇序列
问题描述
小明是一个中学生,今天他刚刚学习了数列。他在纸上写了一个长度为 n 的正整数序列, a 0 , a 1 , … , a n − 1 a_0,a_1,\ldots,a_{n-1} a0,a1,…,an−1。这个数列里面只有 1 和 0,我们将 1 和 0 没有重复跟随并且至少由 3 个数组成的数列的数列称之为「神奇数列」。比如 10101 是一个神奇数列,1011 不是一个神奇数列。他想知道这个序列里面最长的「神奇数列」是哪个,你可以帮帮他吗?
输入格式
- 一行连续的数
s,只有0和1
输出格式
- 一行数
输入样例
0101011101
输出样例
010101
数据范围
- 1 < s . l e n g t h ≤ 5 × 1 0 4 1 < s.length \leq 5 \times 10^4 1<s.length≤5×104
解题思路
- 若
len(inp) < 3,则return ""。 - 遍历该串,使用
count来计数,若出现重复则将count = 0。 - 最终求得
count的最大值就是ans。
代码
func solution3(inp string) string {if len(inp) < 3 {return ""}// Edit your code heremaxn := 0count := 0var ans stringfor i := 1; i < len(inp); i++ {if inp[i] != inp[i-1] {count++} else {if count > maxn {maxn = countans = inp[i-count-1 : i]count = 0}}}return ans
}
总结
目前,此网站OJ还无法进行提交代码,题解样例是过了的。如有问题,可以在评论区提问哦~
相关文章:

字节青训营入营考核部分题解
题库链接:https://juejin.cn/problemset?utm_sourceschool&utm_mediumyouthcamp&utm_campaignexamine 1. 计算从x到y的最小步数 问题描述 AB 实验同学每天都很苦恼如何可以更好地进行 AB 实验,每一步的流程很重要,我们目标为了…...

Android调用系统打印图片
拍摄和分享照片是移动设备最受欢迎的用途之一。如果您的应用 拍摄照片、展示照片或允许用户分享图片,则应考虑启用打印功能 和图片。Android 支持库提供了一个便捷的功能,支持使用 只需编写极少的代码和一组简单的打印版式选项。 本节课介绍如何使用 v4…...

网络最快的速度光速,因此‘‘光网络‘‘由此产生
世界上有一种最快的速度又是光,以前传统以太网络规划满足不了现在的需求。 一 有线网规划 二 无线网规划...
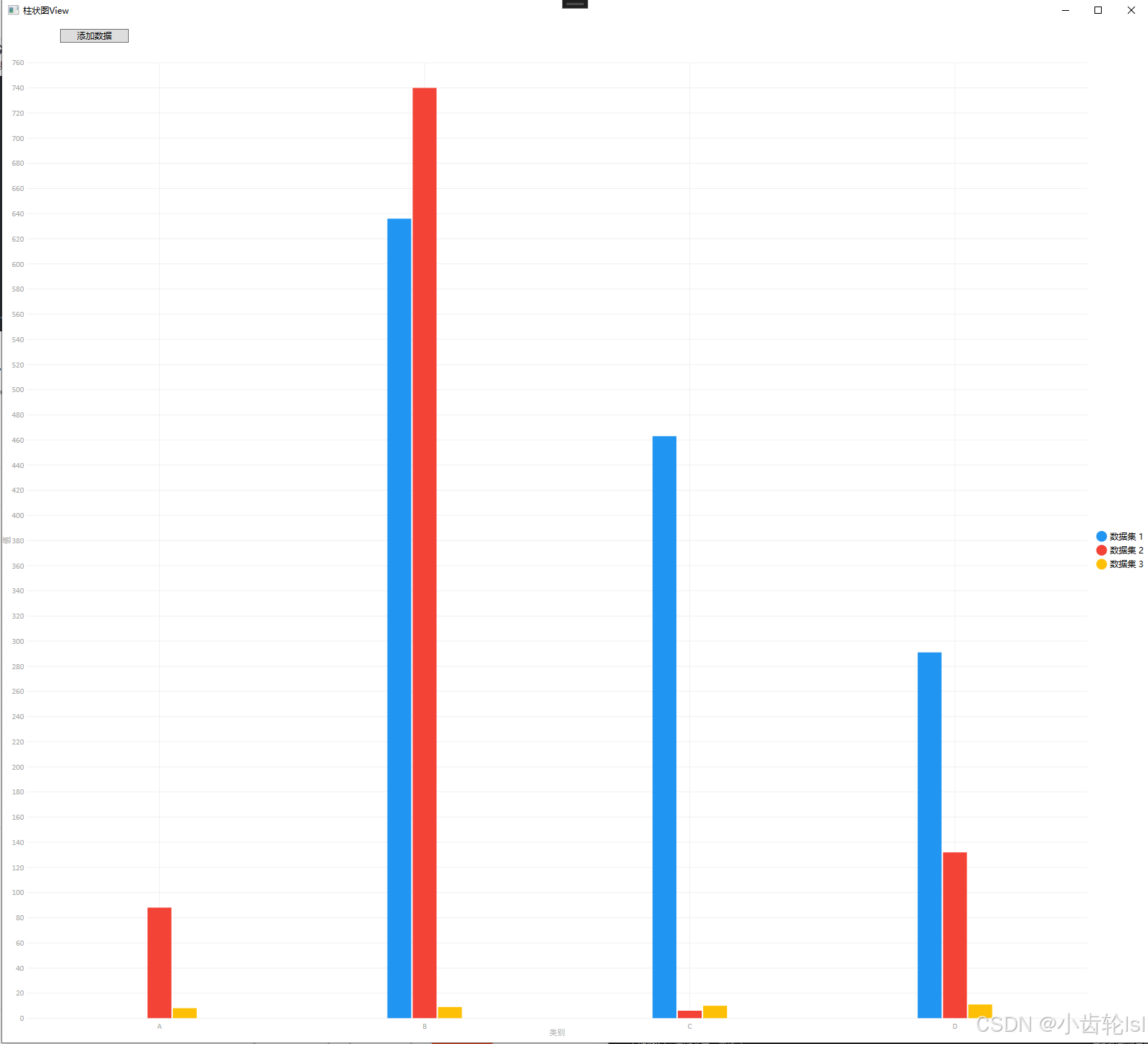
WPF -- LiveCharts的使用和源码
LiveCharts 是一个开源的 .NET 图表库,特别适用于 WPF、WinForms 和其他 .NET 平台。它提供了丰富的图表类型和功能,使开发者能够轻松地在应用程序中创建动态和交互式图表。下面我将使用WPF平台创建一个测试实例。 一、LiveCharts的安装和使用 1.安装N…...

spring 如何将mutipartFile转存到本地磁盘
两者的区别和联系 MutipartFile是spring的一部分,File则是java的标准类MutipartFile用于接收web传递的文件,File操作本地系统的文件 MutipartFile 转换File的三种方式 使用MutipartFile 自带的transferTo方法使用java自带的FileOutPutStream流使用java自…...

【学术会议-6】激发灵感-计算机科学与技术学术会议邀您参与,共享学术盛宴,塑造明天的科技梦想!
【学术会议-6】激发灵感-计算机科学与技术学术会议邀您参与,共享学术盛宴,塑造明天的科技梦想! 【学术会议-6】激发灵感-计算机科学与技术学术会议邀您参与,共享学术盛宴,塑造明天的科技梦想! 文章目录 【…...
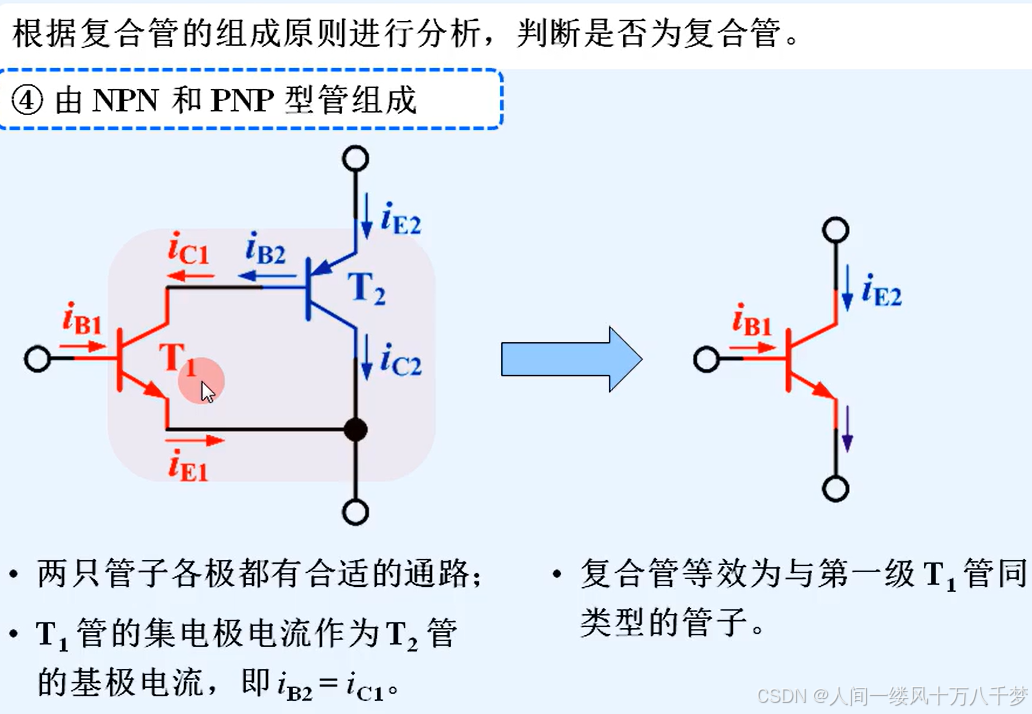
模电基础(晶体管放大电路)
1.放大电路 1.1基本共射放大电路工作原理 1.1.1电路的组成和作用 各器件的作用 (1)(交流电源):输入电路的有用信号,也就是我们需要去放大的信号 (2)(反馈…...
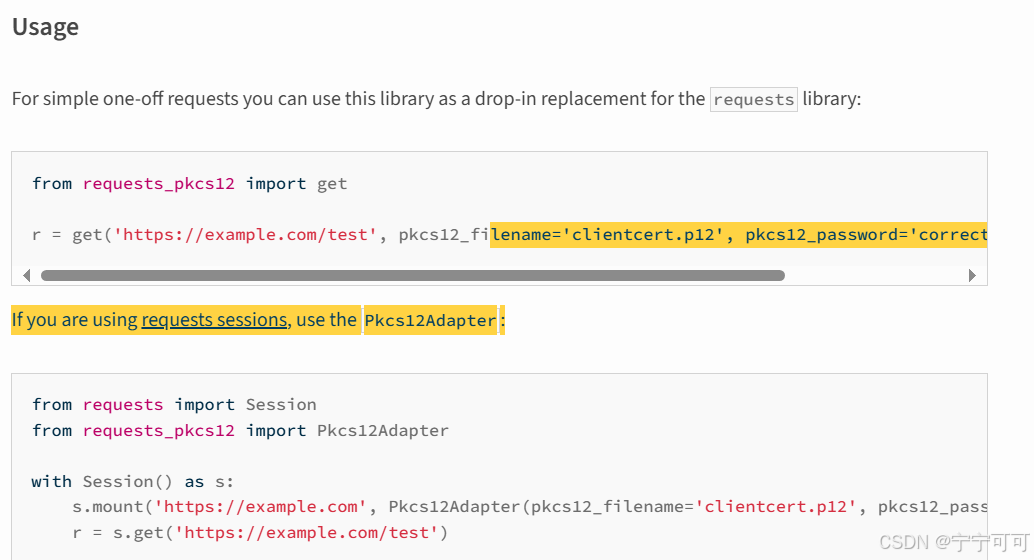
Python3 接口自动化测试,HTTPS下载文件(GET方法和POST方法)
Python3 接口自动化测试,HTTPS下载文件(GET方法和POST方法) requests-pkcs12 PyPI python中如何使用requests模块下载文件并获取进度提示 1、GET方法 1.1、调用 # 下载客户端(GET)def download_client_get(self, header_all):try:url = self.host + "/xxx/v1/xxx-mod…...
rhce:列行性(at和cron)
配置 at练习 设置时间提醒 定义一分钟后显示命令,使用atq查看 cron练习 配置 systemctl status crond 查看文件所在位置 ll /var/spool/cron/ 主要功能 开始操作 进入界面操作每天早上9点说hello crontab -e 五个星号分别代表分时日月周,其次是执…...

kubernetes给service动态增加服务端口
根据kubernetes官方文档的说明,service的ports规则支持merge操作: portsServicePort arraypatch strategy: mergepatch merge key: portThe list of ports that are exposed by this service. More info: https://kubernetes.io/docs/concepts/services-…...
如何将 html 渲染后的节点传递给后端?
问题 现在我有一个动态的 html 节点,我想用 vue 渲染后,传递给后端保存 思路 本来想给html的,发现样式是个问题 在一个是打印成pdf,然后上传,这个操作就变多了 最后的思路是通过 html2canvas 转化成 canvas 然后变成…...
ubuntu24 finalshell 无法连接ubuntu服务器, 客户端无法连接ubuntu, 无法远程连接ubuntu。
场景: 虚拟机新创建一个最小化的ubuntu服务器,使用finalshell连接服务,发现连接不上。 1. 查看防火墙ufw 是否开启,22端口是否放行 2. 查看是否安装openssh server, 并配置 我的问题是安装了openssh server 但是没有配置root可…...

牛客编程初学者入门训练——BC19 牛牛的对齐
BC19 牛牛的对齐 描述 读入 3 个整数,牛牛尝试以后两个数字占 8 个空格的宽度靠右对齐输出。 输入描述: 输入三个整数,用空格隔开。 输出描述: 输出 3 个整数以第二三个数字占 8 个空格靠右对齐输出 示例1 输入:…...

log file sync 内部执行过程
通常oracle的log file sync执行大致印象是等待cpu、log file parallel write、等待cpu,遇到问题主要考虑lgwr自适应模式参数要关闭、io性能、cpu瓶颈、归档数量和大小等,但是内部执行内容其实很多,尤其是有ADG了以后。 log file sync主要执行…...
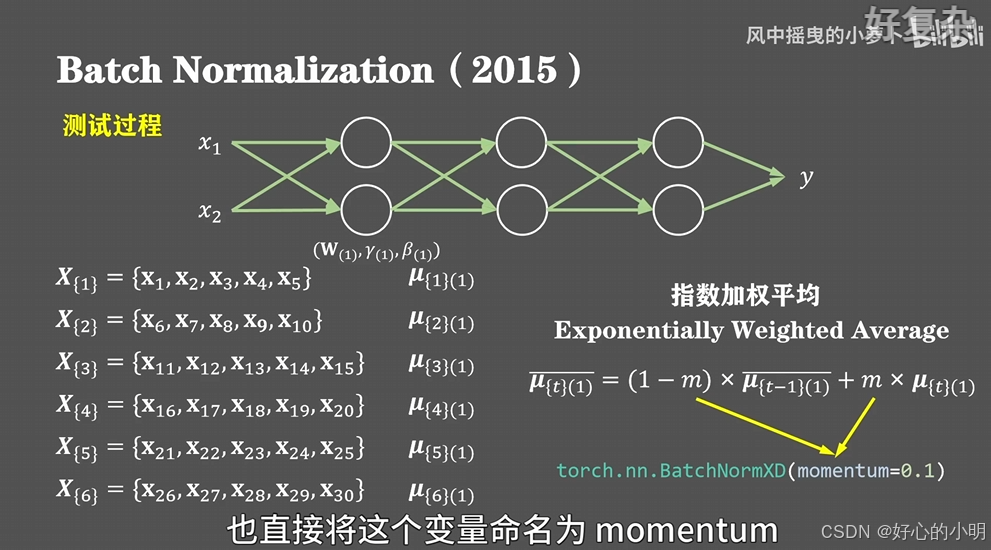
【动手学深度学习】7.5 批量规范化(个人向笔记)
训练深层神经网络是十分困难的,特别是在较短的时间内使它们收敛更加棘手。而本节的批量规范化(batch normalization) 可以持续加速深层网络的收敛速度结合下节会介绍道德残差块,批量规范化使得研究人员能够训练100层以上的网络 1.…...

111 - exercise 5
一 public class Dummy {private static int a 3;private static int b 5;private static int c 7;public static void main(String... arguments) {int a 1, b 2;System.out.println("" a (a - b) c);} }这个Java程序中有两个a和b变量,一个是类…...
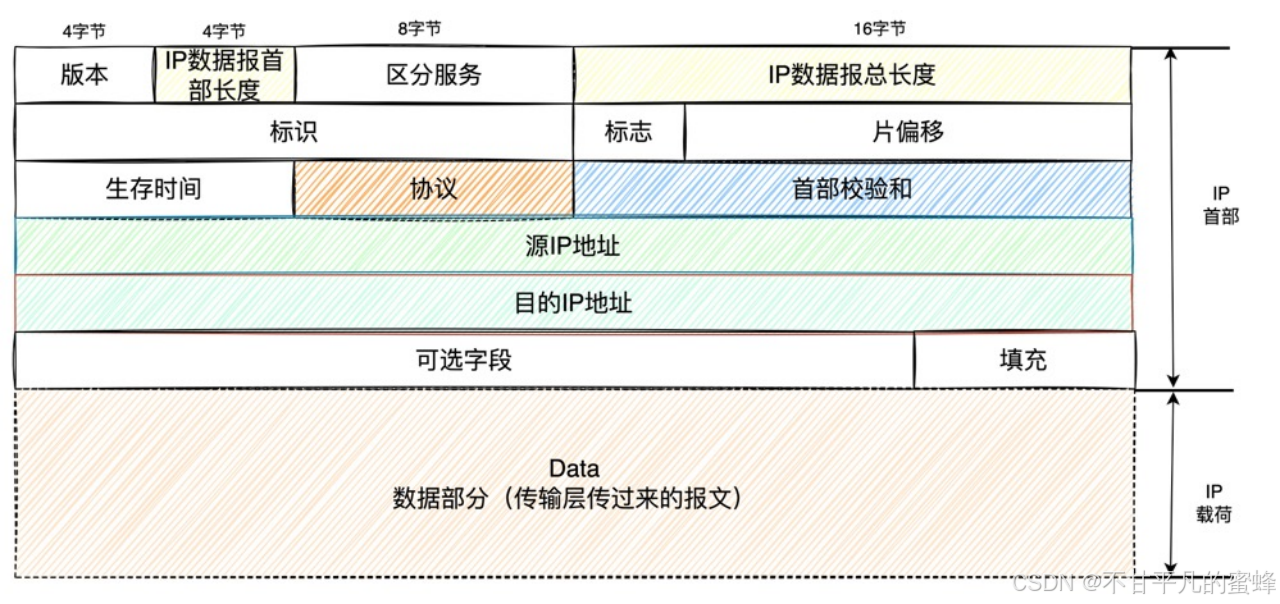
第二十五:IP网络层的数据,IP数据报
在数据链路层传输的数据叫帧,帧是数据链路层的传输单元。 那么在IP网络层的数据也有一个叫法IP数据报。 IP数据报 IP数据报首部 数据。 数据是传输层传递过来的报文;IP数据报首部格式如下: IP 报头的最小长度为 20 字节,上图…...

三菱FX3UPLC机械原点回归- DSZR/ZRN指令
机械原点回归用指令的种类 产生正转脉冲或者反转脉冲后,增减当前值寄存器的内容。可编程控制器的定位指令,可编程控制器的电源0FF后,当前值寄存器清零,因此上电后,请务必使机械位置和当前值寄存器的位置相吻合…...
粘包现象解决方案、socketserver实现并发)
网络通信与并发编程(三)粘包现象解决方案、socketserver实现并发
粘包现象解决方案、socketserver实现并发 文章目录 粘包现象解决方案、socketserver实现并发一、粘包现象解决方案1.发送数据大小2.发送数据信息 二、socketserver实现并发1.tcp版的socketserver并发2.udp版的socketserver并发 一、粘包现象解决方案 1.发送数据大小 有了上一…...

使用Uniapp开发微信小程序实现一个自定义的首页顶部轮播图效果?
在Uniapp中开发微信小程序,并实现自定义首页顶部轮播图的效果,可以通过使用Uniapp的组件如swiper和swiper-item来完成。这是一个常见的需求,下面是一个完整的示例代码,展示如何实现一个简单的自定义轮播图效果。 创建页面结构 首…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程(6.3)
目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 编辑编辑 UDP的特征 socke函数 bind函数 recvfrom函数(接收函数) sendto函数(发送函数) 五、网络编程之 UDP 用…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...
