C语言笔记(数据的存储篇)
目录
1.数据类型的详细介绍
2.整型在内存中的存储:原码、反码、补码
3.大小端字节序介绍及判断
4.浮点型的内存中的存储解析
1.数据类型的详细介绍
下述是内置类型:
char // 字符数据类型
short // 短整型
int // 整型
long // 长整型
long long // 更长的整型
float // 单精度浮点型
double //双精度浮点型在这里就不说不同数据类型在内存中所占数据类型大小了。注意的是C语言中的没有字符串的数据类型
数据类型的意义
1.使用数据类型开辟内存空间的大小;
2.如何看待内存空间的视角。
整形家族:
char
unsigned char //字符在存储的时候存储的是ASCLL码值A,ASCLL是整数,
signed char //所以在归类的时候,字符属于整型家族short
unsigned short [int]
signed short [int]int
unsigned int
signed intlong
unsigned long [int]
signed long [int] //[]中的数据类型是可以省略的注意, char是signed char还是unsigned char 是取决于编译器的。常见的编译器上char的类型就是signed char。
数据元素个数和数组的名字发生变化,数组的类型也会发生变化。
浮点数家族:
float
double构造类型
> 数组类型
> 结构体类型 struct
> 枚举类型 enum
> 联合类型 union指针类型
int *pi;
char *pc;
float* pf;
void* pv;void 表示空类型以为就是没有什么类型,可以用于函数的返回类型、函数的参数、指针类型。
2.整型在内存中的存储:原码、反码、补码
正整型的原反补码都是相同的,但负整型数据的反码要符号位不变其他位置取反,加上1就会变成补码,如下 : 补码也可以先取反再+1得到原码。负整型补码转变成原码有两种方式。
-1//32位机器
原码 10000000 00000000 00000000 00000001
反码 11111111 11111111 11111111 11111110
补码 11111111 11111111 11111111 11111111补码转原码
//方式1
补码 11111111 11111111 11111111 11111111
反码 11111111 11111111 11111111 11111110 -1
原码 10000000 00000000 00000000 00000001 取反//方式2
补码 11111111 11111111 11111111 11111111
中间 10000000 00000000 00000000 00000000 取反
原码 10000000 00000000 00000000 00000001 +1整形数据在内存中是以二进制补码的形式来存放的。本例子列举的是32位机器中的存储。
int a = 20;// 20
// 00000000 00000000 00000000 00010100--原码
// 00000000 00000000 00000000 00010100--反码
// 00000000 00000000 00000000 00010100--补码
// 0x00 00 00 14 转换成16进制 在看看存储int b= -10;
// -10
// 10000000 00000000 00000000 00001010--原码
// 11111111 11111111 11111111 11110101--反码
// 11111111 11111111 11111111 11110110--补码
// 0xff ff ff f6 转换成16进制int a = 20;在VS2017下的存储方式

int b = -10;在VS2017下的存储方式

例题,下属例题都是判断输出什么的
1.
#include <stdio.h>
int main()
{char a = -1;//10000000 00000000 00000000 00000001 原码//11111111 11111111 11111111 11111110 反码//11111111 11111111 11111111 11111111 补码//11111111 截断,将一个整型数值赋予一个字符变量的时候要截断//11111111 11111111 11111111 11111111 补码// 因为要输出的是整型,应该整型提升,有符号位置应该按照符号位来提升 1 补1 0补0//10000000 00000000 00000000 00000000 取反//10000000 00000000 00000000 00000001 原码signed char b = -1;//和上面相同//10000001 unsigned char c = -1;//10000000 00000000 00000000 00000001 原码//11111111 11111111 11111111 11111110 反码//11111111 11111111 11111111 11111111 补码//11111111 截断//00000000 00000000 00000000 11111111 //整型提升 无符号为整型提升 补0//存储方式是一样的,但输出的方式是不一样的 printf("a=%d,b=%d,c=%d", a, b, c); // -1 ,-1,255return 0;
}2.
#include <stdio.h>
int main()
{char a = -128;
//10000000 00000000 00000000 10000000 原码
//11111111 11111111 11111111 01111111 反码
//11111111 11111111 11111111 10000000 补码
//截取 10000000
//整型提升 看char是有符号的char 整型提升是看原来的数据类型来提升的
//11111111 11111111 11111111 10000000 //输出的是无符号数,可以直接输出,无符号数只有正的printf("%u\n", a);// 4294967168return 0;
}3.
int main()
{char a = 128;// 00000000 00000000 00000000 10000000// 10000000 截断// 11111111 11111111 11111111 10000000 整型提升printf("%u\n", a);return 0;
}4.
int main()
{int i = -20;//10000000 00000000 00000000 00010100 原码//11111111 11111111 11111111 11101011 反码//11111111 11111111 11111111 11101100 补码unsigned int j = 10;//00000000 00000000 00000000 00001010 原码 补码//11111111 11111111 11111111 11110110//10000000 00000000 00000000 00001001//10000000 00000000 00000000 00001010 //-10printf("%d\n", i + j);//-10 //输出的形式有符号数 相加之后本来是无符号数的return 0;
}5.
#include <stdio.h>
#include <windows.h>
int main()
{unsigned int i;for (i = 9; i >= 0; i--) //会无限制的循环,i不可能是负数的,因此会一直大于0{printf("%u\n", i);Sleep(100);} return 0;
} //可以执行一下 从零之后就是一个更大的数字了
6
#include <stdio.h>
int main()
{char a[1000];int i;for (i = 0; i < 1000; i++){a[i] = -1 - i; }//-1 -2 .......-128 127 126 3 2 1 0 128+127=255printf("%d", strlen(a)); //找到'\0' 其ASCLL码值为 0 找到0 return 0;
}7.
#include <stdio.h>
unsigned char i = 0;
int main()
{for (i = 0; i <= 255; i++){printf("hello world\n");//死循环}return 0;
}循环限制条件是无符号数,是一定要注意,设置的限制条件一定要大于0。
3.大小端字节序介绍及判断
大端(存储)模式,是指数据的低位保存在内存的高地址中,而数据的高位,保存在内存的低地址中;
小端(存储)模式,是指数据的低位保存在内存的低地址中,而数据的高位,,保存在内存的高地址中。
为什么会存在大端存储和小端存储呢?
其思想源于格列夫游记,两个国家由于鸡蛋应该是先从大头剥还是从小头处开始剥皮的问题开始了战争。
小端存储,举一个例子,下面是一个数
int a = 0x11223344;下面就是数据在VS2017的存储方式。

数据的低位应该是这样理解的,123 3就是这个数据的低位。看数据的低位放在了低地址上,数据的高位放在了高地址上。
做个表格详细了解一下
| 地址 | 0x007EFBFC | 0x007EFBFD | 0x007EFBFE | 0x007EFBFE |
| 小端存储 | 44 | 33 | 22 | 11 |
| 大端存储 | 11 | 22 | 33 | 44 |
| 低地址 | 高地址 | |||
我们再写一个小程序来判断一个编辑器是大端存储还是小端存储。
#include <stdio.h>
int main()
{int a = 1;//存储方式是 0x00 00 00 01 如果只取一个字节就比较好判断了char *pa = (char *)&a;//()括号中的强制类型转化if (*pa == 1){printf("小端存储\n");}else{printf("大端存储\n");}return 0;
}还可以将这个逻辑封装到一个函数中,大家可以练习一下,在以后的时候中好的函数是经常调用的。
封装函数
void check_byte()
{int a = 1;if ((char *)&a)printf("小端存储\n");elseprintf("大端存储\n");
}4.浮点型的内存中的存储解析
大家想一下 3.14159, 1E10.在内存中是如何存储的?当然和整型是不一样的。先看下面的例子。
int main()
{
int n = 9;
//00000000 00000000 00000000 00001001
float *pFloat = (float *)&n;
printf("n的值为:%d\n",n);
printf("*pFloat的值为:%f\n",*pFloat);
//以浮点数的存储方式取出是不正常值,两者存储的方式是不一样的,*pFloat = 9.0;
printf("num的值为:%d\n",n);
printf("*pFloat的值为:%f\n",*pFloat);
return 0;
}以下是上述代码的值,可以往后看看浮点型是如何存储的就理解了,在文章的最后会有解析的。

浮点数的存储规则
根据国际标准IEEE(电气和电子工程协会) 754,任意一个二进制浮点数V可以表示成下面的形式:
>. (-1)^S * M * 2^E
>. (-1)^s表示符号位,当s=0,V为正数;当s=1,V为负数。
>. M表示有效数字,大于等于1,小于2。
>. 2^E表示指数位
举个例子就明白了,
将十进制的 5.0 1> 转换成二级制101.1,相当都1.01×2^2
按上述的格式就是 S=0,表示正数;M=1.01,E=2。如果是-5的话那就是S=-1了。
再来一个 5.5= 101.1二进制 , 转换成科学计数法 1.011*2^2 (-1)^0*1.011*2^2
S=0, M=1.011, E=2。 0.5 大家思考一下 注意一下(浮点数中没有原反补的概念)

单精度浮点数存储模型(4byte)

双精度浮点型(8byte)
特殊规定
1. M值的存储方式
前面说过, 1≤M<2 ,也就是说,M可以写成 1.xxxxxx 的形式,其中xxxxxx表示小数部分。IEEE 754规定,在计算机内部保存M时,默认这个数的第一位总是1,因此可以被舍去,只保存后面的xxxxxx部分。 (此种方式可以提升精度)
比如保存1.01的时候,只保存01,等到读取的时候,再把第一位的1加上去。这样做的目的,是节省1位有效数字。以32位浮点数为例,留给M只有23位,将第一位的1舍去以后,等于可以保存24位有效数字。
2. E的存储方式
E为一个无符号整数是无法判读E是正负的。如果E为8位,它的取值范围为0~255;如果E为11位,它的取值范围为0~2047。但是科学计数法中的E是可以出现负数的,所以IEEE 754规定,存入内存时E的真实值必须再加上一个中间数,对于8位的E,这个中间数是127;对于11位的E,这个中间数是1023。比如,2^10的E是10,所以保存成32位浮点数时,必须保存成10+127=137,即10001001。
指数E从内存中中取出还可以再分为三种情况
1.E不全为0或者不全为1
这时,浮点数就采用下面的规则表示,即指数E的计算值减去127(或1023),得到真实值,再有效数字M前加上第一位的1。 比如: 0.5(1/2)的二进制形式为0.1,由于规定正数部分必须为1,即将小数点右移1位,则为1.0*2^(-1),其阶码为-1+127=126,表示为01111110,而尾数1.0去掉整数部分为0,补齐0到23位00000000000000000000000,则其二进制表示形式为:
0 01111110 000000000000000000000002.E全为0
这时,浮点数的指数E等于1-127(或者1-1023)即为真实值, 有效数字M不再加上第一位的1,而是还原为0.xxxxxx的小数。这样做是为了表示±0,以及接近于0的很小的数字。
3.E全为1
这时,如果有效数字M全为0,表示±无穷大(正负取决于符号位s).
实际的例子
5.5
float f = 5.5f;// 转换成SME的形式 (-1)^0 * 1.011 * 2^2//S = 0;M = 1.011; E = 2; 2+127=129//0 10000001 01100000000000000000000//0100 0000 1011 0000 0000 0000 0000 0000// 4 0 b 0 0 0 0 04.小节开始的例题
#include <stdio.h>
int main()
{int n = 9;float *pFloat = (float *)&n;//00000000 00000000 00000000 00001001//0 00000000 0000000 00000000 00001001//(-1)^0 * 0.00000000000000000001001 * 2^-126 相当于0了printf("n的值为:%d\n", n);printf("*pFloat的值为:%f\n", *pFloat);*pFloat = 9.0;//9.0的存储方式//1001二级制 1.001^3 3+127=130//0 1000 0010 00100000000000000000000//01000001000100000000000000000000 存储方式printf("num的值为:%d\n", n);printf("*pFloat的值为:%f\n", *pFloat);//1,091,567,616return 0;
}由于存储方式的不同和访问方式的不同,会造成数据错误。
相关文章:

C语言笔记(数据的存储篇)
目录 1.数据类型的详细介绍 2.整型在内存中的存储:原码、反码、补码 3.大小端字节序介绍及判断 4.浮点型的内存中的存储解析 1.数据类型的详细介绍 下述是内置类型: char // 字符数据类型 short // 短整型 int // 整型 long …...

wsl: 检测到 localhost 代理配置,但未镜像到 WSL。NAT 模式下的 WSL 不支持 localhost 代理的解决方法
前言 开头先讲讲wsl2启用代理的必要性,一般来说,会用wsl的都是开发者,那么就避免不了从网络上下载软件和应用,但是由于众所周知的原因,你使用apt,wget等工具下载国外网站的东西时,下载速度就会…...

CSS 居中那些事
一、父子元素高度确定 简单粗暴, 直接通过设置合适的 padding 或 margin 实现居中 <style>.p {padding: 20px 0;background: rgba(255, 0, 0, 0.1);}.c {width: 40px;height: 20px;background: blue;} </style> <div class"p"><div class"…...

Java项目-基于springboot框架的智能热度分析和自媒体推送平台项目实战(附源码+文档)
作者:计算机学长阿伟 开发技术:SpringBoot、SSM、Vue、MySQL、ElementUI等,“文末源码”。 开发运行环境 开发语言:Java数据库:MySQL技术:SpringBoot、Vue、Mybaits Plus、ELementUI工具:IDEA/…...

跨平台进程池背后的思想
背景是基于业务需求,需要实现一个跨平台的项目。项目中由于有部分功能存在大量计算,所以打算单独分配一个进程去进行计算。 进程池的实现与线程池的实现逻辑上如出一辙。但是实现上进程池的实现会比线程池实现复杂的多,主要比较复杂的点的就在于并发安全的任务队列。…...

前端性能优化之加载篇
前端页面加载的过程其实跟我们常常提起的浏览器页面渲染流程几乎一致: 网络请求,服务端返回 HTML 内容。 浏览器一边解析 HTML,一边进行页面渲染。 解析到外部资源,会发起 HTTP 请求获取,加载 Javascript 代码时会暂停页面渲染。 根据业务代码加载过程,会分别进入页面开始…...
数据结构(栈)
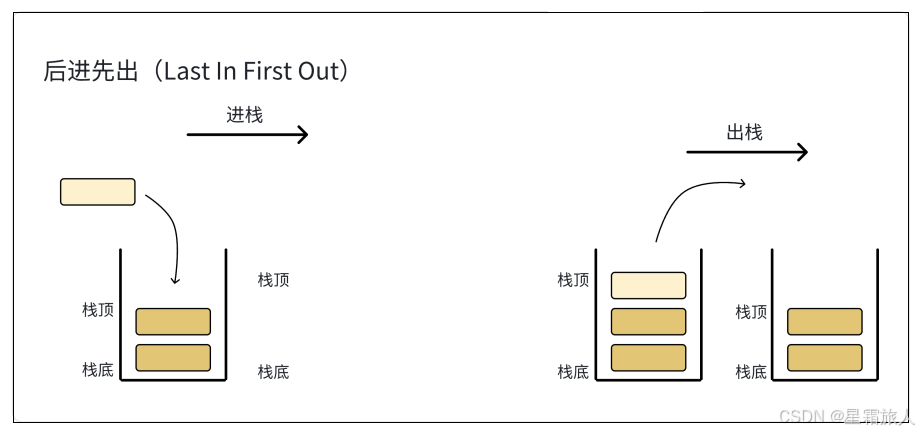
每当误会消除冰释前嫌的时候,故事就距离结尾不远了。 栈 概念与结构 1. 栈⼀种特殊的线性表,其只允许在固定的⼀端进行插入和删除元素操作。 2. 进行数据插入和删除操作的⼀端称为栈顶,另⼀端称为栈底。 3. 栈中的数据元素遵守后进先出的原则…...
Aspose.PDF功能演示:使用 JavaScript 从 PDF 中提取文本
在数据提取、业务文档自动化和文本挖掘方面,使用 JavaScript 从PDF中提取文本非常有用。它允许开发人员自动执行从 PDF 收集信息的过程,从而显著提高处理大量文档的生产力和效率。在这篇博文中,我们将学习如何使用 JavaScript 从 PDF 中提取文…...

计算机系统简介
一、计算机的软硬件概念 1.硬件:计算机的实体,如主机、外设、硬盘、显卡等。 2.软件:由具有各类特殊功能的信息(程序)组成。 系统软件:用来管理整个计算机系统,如语言处理程序、操作系统、服…...

学习文档10/18
MySQL高性能优化规范: 数据库命名规范 所有数据库对象名称必须使用小写字母并用下划线分割所有数据库对象名称禁止使用 MySQL 保留关键字(如果表名中包含关键字查询时,需要将其用单引号括起来)数据库对象的命名要能做到见名识意…...

Redis入门到精通(二):入门Redis看这一篇就够了
文章目录 一、Redis的双写一致性1.延迟双删2.添加分布式锁3.异步监听可靠消息基于MQ消息队列的异步监听基于Canal的异步通知 二、Redis的持久化持久化流程1.RDB机制1.1save1.2bgsave1.3自动触发 2.AOF机制三种触发机制3.RDB和AOF的对比 三、Redis的数据删除策略1.惰性删除2.定期…...

荒岛逃生游戏
题目描述 一个荒岛上有若干人,岛上只有一条路通往岛屿两端的港口,大家需要逃往两端的港口才可逃生。 假定每个人移动的速度一样,且只可选择向左或向右逃生。 若两个人相遇,则进行决斗,战斗力强的能够活下来ÿ…...

玫瑰花HTML源码
HTML源码 <pre id"tiresult" style"font-size: 9px; background-color: #000000; font-weight: bold; padding: 4px 5px; --fs: 9px;"><b style"color:#000000">0010000100000111101110110111100010000100000100001010111111100110…...

【wpf】07 后端验证及令牌码获取步骤
由于在用wpf开发应用程序时,从后端获取数据需要用到 Authorization 授权的Bearer令牌,而这个令牌的获取需要登录后台进行获取,这里登录时还涉及到的验证码的操作,所以在获取过程中,需要对后台系统进行登录并拿到这个Be…...

学习中,师傅b站泷羽sec——xss挖掘过程
某职业技术学院网站xss挖掘: 资产归纳 例如:先把功能点都看一遍,大部分都是文章 根据信息搜集第一课学习到一般主站的防御力是比较强的,出现漏洞的点不是对新手不友好。 在资产验证过程中还是把主站看了一遍 没有发现有攻击的机会…...

什么是双因素身份验证?双因素身份验证的凭据类型有哪些?
w微服务在数字化的时代,保护个人和企业的敏感信息至关重要。双因素身份验证(Two-Factor Authentication,简称 2FA)作为一种增强安全性的方法,越来越受到广泛关注。那么,什么是双因素身份验证呢?…...

【MR开发】在Pico设备上接入MRTK3(一)——在Unity工程中导入MRTK3依赖
写在前面的话 在Pico上接入MRTK3,目前已有大佬开源。 https://github.com/Phantomxm2021/PicoMRTK3 也有值得推荐的文章。 MRTK3在PICO4上的使用小结 但由于在MacOS上使用MRTK3,无法通过Mixed Reality Feature Tool工具管理MRTK3安装包。 故记录一下…...

利用移动式三维扫描技术创建考古文物的彩色纹理网格【上海沪敖3D】
文章来源于蔡司工业质量解决方案,作者蔡司工业质量 在考古环境中,三维扫描技术应用广泛,如存档、保存、复制和分享(包括实体和虚拟形式)。 文中,通过真实的扫描案例,您将了解到三维光学解决方案…...
)
Spring AI Java程序员的AI之Spring AI(四)
Spring AI之Java经典面试题智能小助手 前言一、准备面试题二、搭建工程三、文件读取与解析四、Markdown文件解析五、问题搜索六、自定义EmbeddingClient七、定义请求Controller 前言 通过Ollama在本地部署了Llama3大模型,这篇来基于Llama3和Spring AI,以…...

精选20个爆火的Python实战项目(含源码),直接拿走不谢!
今天给大家介绍20个非常实用的Python项目,帮助大家更好的学习Python。 完整版Python项目源码,【点击这里】领取! ① 猜字游戏 import random def guess_word_game(): words ["apple", "banana", "cherry&quo…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...
