【C++ 算法进阶】算法提升四
数组查询问题 (数组优化)
题目
数组为 {3 , 2, 2 ,3 ,1} 查询为(0 ,3 ,2)
这个查询的意义是 在数组下标0~3这个范围上 有多少个2 (答案为2)
假设现在给你一个数组arr 假设我们对于这个数组的查询十分频繁
现在要求你返回所有的查询结果
题目分析
我们可以看到题目中有 对于这个数组的查询十分频繁 这句描述
看到之后我们自然就可以想到我们要做一个预处理数组来让查询的代价尽可能的低 (现在的代价是O(M)) M为查询数组的长度
这里提供两个预处理数组的思路
- 因为每次给的范围是随机的 所以说我们从数字入手 对于每个数字建立一张下标表 以后每次查询的时候只需要通过二分法找到范围内数字的下标即可 这样我们的时间复杂度就成为了二分法的时间复杂度
- 我们可以从数字的范围开始入手 对于每个数字统计它在0~N范围上出现的次数 以后假设我们需要求从 J到K上某个数字出现的次数就只需要让这个数组的K位置的数字减去J位置的数字即可 这样的时间复杂度就是O(1)了
我们这里提供方法二的解
代码解析
这里需要注意的是
for (auto& it : map)
上面这一行代码 如果我们没有写& 那么他就是值遍历 导致我们下面的修改没有事实上修改map数组内的数据
int main() {vector<int> arr = {3 ,2 ,2 , 3, 1};// 这里建立N个数组 每个数组和arr一样长 代表从0开始到当前位置有多少个当前数unordered_map<int, vector<int>> map;for (auto x : arr){if (map.count(x) == 0){map[x] = vector<int>(arr.size(), 0);}}// 开始填表 for (auto& it : map){int count = 0;for (int i = 0; i < arr.size(); i++){if (it.first == arr[i]){count++;}it.second[i] = count;}}cout << map[2][3] - map[2][1] << endl;return 0;
}
子数组的最大累加和 (经典动态规划)
题目
本题为LC原题 题目如下

题目分析
这是一道最经典的动态规划问题 是一个以i为结尾位置的模型
我们只需要使用一个dp数组 记录下从0开始的每个位置为结尾时 能够获取的最大值是多少即可
因为子数组的结尾肯定是在原数组中的 所以说我们计算每个位置作为结尾的最大和肯定能算出最终答案
代码解析
本题没有什么难点
class Solution {
public:int maxSubArray(vector<int>& nums) {if (nums.size() == 1) {return nums[0];}// 首先创建一个dp数组vector<int> dp(nums.size() , 0);dp[0] = nums[0];for (int i = 1 ; i < nums.size(); i++) {dp[i] = dp[i-1] < 0 ? nums[i] : dp[i-1] + nums[i];}int max = dp[0];for (auto x : dp) {if (x >max) {max = x;}}return max;}
};
二维数组 子矩阵的最大累加和 (数组压缩 + 动态规划)
题目
返回一个二维数组中 子矩阵的最大累加和 此题为LC原题 题目如下

题目分析
这道题其实就是我们第二题的变种
思路相同 : 如果我们要求一个子矩阵和的最大值 那么我们可以将问题转化成
求以每一行作为矩阵的头 往下扩展时 矩阵的最大值
因为矩阵肯定在二维数组内 所以说只要我们求出以每一行作为起始的最大值 就能求出最终的答案
数组压缩技巧
当我们求第一行时 我们可以直接照搬上一题的代码
当我们求第一行到第N行时 因为我们求的是和 所以说我们可以将各列的代码相加 组成一个新的数组 再使用第一行的技巧
代码详解
class Solution {
public:vector<int> getMaxMatrix(vector<vector<int>>& matrix) {int N = matrix.size();int M = matrix[0].size(); int a = 0;int begin = 0;int c = 0;int d = 0;int max = INT_MIN;for (int i = 0; i < N; i++) {vector<int> arr(M , 0);for (int j = i; j < N;j++) {int cur = 0;int b = 0; // 这个值要变化for (int k = 0; k < M; k++) {arr[k] += matrix[j][k];cur += arr[k];if (cur > max) {max = cur;a = i;begin = b;c = j;d = k;}if (cur < 0) {cur = 0;b = k + 1;}}}}return {a , begin, c, d};}
};
子序列的最大累加和 (动态规划)
题目
返回一个数组中 选择的数字不能相邻的情况下 最大子序列的累加和
题目分析
这里提供给大家一个思路 只要我们看到 子序列 这几个字 我们就要想到这是一种从左到右的尝试模型
我们可以定义一个函数 int process(vector<int>& arr, int index, vector<int>& memo) 该函数能否返回在index位置的时候子序列的最大累加和
那么接下来我们就只需要列出边界和各种的可能性即可
代码详解
#include<iostream>
using namespace std;
#include<vector>int process(vector<int>& arr, int index, vector<int>& memo) {if (index >= arr.size()) {return 0;}// 如果已经计算过,直接返回if (memo[index] != -1) {return memo[index];}// 选择当前数字并跳过下一个数字int p1 = arr[index] + process(arr, index + 2, memo);// 不选择当前数字int p2 = process(arr, index + 1, memo);// 记录结果memo[index] = max(p1, p2);return memo[index];
}int getMaxSumNonAdjacent(vector<int>& arr) {if (arr.empty()) {return 0;}vector<int> memo(arr.size(), -1); // 用于记忆化的数组return process(arr, 0, memo);
}
糖果问题 (贪心)
题目
本题为LC原题 题目如下

题目分析
这个问题是一种贪心问题
相邻的两个孩子评分更高的孩子会获得更多的糖果
- 左规则:当 ratings[i−1]<ratings[i] 时 i 号学生的糖果数量将比 i−1 号孩子的糖果数量多
- 右规则:当 ratings[i]>ratings[i+1] 时 i 号学生的糖果数量将比 i+1 号孩子的糖果数量多
所以说我们可以将这个数组遍历两次
- 从左到右遍历 遇到比前一个位置大的糖果就++ 否则糖果归1
- 从右到左遍历 遇到比前一个位置大的糖果就++ 否则糖果归1
之后我们将这两次遍历的结果取较大值即可 (因为要同时满足这两个条件)
代码详解
class Solution {
public:int candy(vector<int>& ratings) {int M = ratings.size();vector<int> left(M , 0);vector<int> right(M , 0);left[0] = 1;for (int i = 1 ; i < M; i++) {if (ratings[i] > ratings[i-1]) {left[i] = left[i-1] + 1;} else {left[i] = 1;}}right[M - 1] = 1;for (int i = M - 2; i >=0 ; i--) {if (ratings[i] > ratings[i+1]) {right[i] = right[i+1] + 1;} else {right[i] = 1;}}for (int i = 0; i < M; i++) {left[i] = left[i] > right[i] ? left[i] :right[i];}int max = 0;for (auto x : left) {max += x;}return max;}
};
生成数组(分治)
题目
给定一个正数为size 生成长度为size的达标数组
达标: 对于任意的 i < k < j 满足 [I] + [J] != 2*[K]
题目分析
这是一道典型的分治问题 想到这种思路的过程挺难的 这里直接提供思路
假设一个数组达标 那么这个数组的两倍肯定也达标 这个数组的两倍+1肯定也达标 (自己使用公式验证下就能明白)
那么数组的两倍 再加上这个数组的两倍+1 组成的一个新数组 肯定也达标
这是为什么呢?
因为我们如果从这个数组的左边或者右边任意选一个数相加 那么他们相加肯定是奇数 而最后要达标则要是偶数2*[K]
所以说我们可以从一个数开始 二倍二倍的往上扩 自然就能求出最终答案
如果不是2的n次方怎么办呢?
只需要舍弃掉后面多余的数字即可
代码详解
vector<int> process(int size) {if (size == 1) {return { 1 };}int halfsize = (size + 1) / 2;vector<int> half = process(halfsize);// 构造出一个完成的数组// 一半是奇数 一半是偶数vector<int> ans;for (int i = 0; i < halfsize; i++) {ans.push_back(half[i] * 2 + 1);}for (int i = halfsize; i < size; i++) {ans.push_back(half[i - halfsize] * 2);}return ans;
}int main() {vector<int> ans = process(9);for (auto x : ans) {cout << x << endl;}return 0;
}字符串交错组成 (动态规划 – 样本对应模型)
题目
此题为LC原题目 题目如下

题目分析
遇到这种多个字符串问题 我们第一时间想到的就是要用动态规划的样本对应模型去解决
首先设置一个process函数
bool process(string& s , string& s1 , string&s2 , int index1 , int index2)
这个函数的含义是 从s1的第index1个位置 s2的第index2个位置开始 能否组成字符串s
之后我们只需要考虑三种情况
- 终止条件
- 越界情况
- 有几种可能性
代码详解
class Solution {
public:// 带有记忆化搜索的递归函数bool process(string& s1, string& s2, string& s3, int index1, int index2, vector<vector<int>>& dp) {// 如果 s1 和 s2 的字符都处理完了,且正好匹配了 s3 的长度if (index1 == s1.size() && index2 == s2.size()) {return true;}// 检查越界情况if (index1 > s1.size() || index2 > s2.size()) {return false;}// 如果 dp 中已经计算过该状态,直接返回存储的结果if (dp[index1][index2] != -1) {return dp[index1][index2];}// 当前字符在 s3 中的位置int sIndex = index1 + index2;// 尝试从 s1 中取字符bool p1 = false;if (index1 < s1.size() && s1[index1] == s3[sIndex]) {p1 = process(s1, s2, s3, index1 + 1, index2, dp);}// 尝试从 s2 中取字符bool p2 = false;if (index2 < s2.size() && s2[index2] == s3[sIndex]) {p2 = process(s1, s2, s3, index1, index2 + 1, dp);}// 存储结果:如果 p1 或 p2 为 true,存储 1;否则存储 0dp[index1][index2] = (p1 || p2);return dp[index1][index2];}// 主函数入口bool isInterleave(string s1, string s2, string s3) {// 边界条件检查:如果 s3 的长度不等于 s1 和 s2 长度之和,返回 falseif (s3.size() != s1.size() + s2.size()) {return false;}// 初始化 dp 数组,值全为 -1,表示尚未计算vector<vector<int>> dp(s1.size() + 1, vector<int>(s2.size() + 1, -1));// 从 index1 = 0, index2 = 0 开始return process(s1, s2, s3, 0, 0, dp);}
};
大楼轮廓线问题 ()
相关文章:

【C++ 算法进阶】算法提升四
数组查询问题 (数组优化) 题目 数组为 {3 , 2, 2 ,3 ,1} 查询为(0 ,3 ,2) 这个查询的意义是 在数组下标0~3这个范围上 有多少个2 (答案为2&…...

多种方式实现安全帽佩戴检测
为什么要佩戴安全帽 在探讨安全帽佩戴检测之前,我们先来了解下安全帽佩戴的必要性: 保护头部免受外力伤害 防止物体打击 在建筑施工、矿山开采、工厂车间等场所,经常会有高空坠物的风险。例如在建筑工地上,可能会有工具、材料、…...

基于PHP+MySQL+Vue的网上订餐系统
摘要 本文介绍了一个基于PHPMySQLVue技术的网上订餐系统。该系统旨在为用户提供便捷的在线订餐服务,同时提高餐厅的运营效率。系统后端采用PHP语言开发,利用MySQL数据库进行数据存储与管理,实现了用户注册登录、菜品浏览、购物车管理、订单提…...

Vue学习笔记 Class绑定 Style绑定 侦听器 表单输入绑定 模板引用 组件组成 组件嵌套关系
文章目录 Class绑定绑定对象绑定数组注意事项 style绑定绑定对象代码效果展示 绑定数组 侦听器注意的点代码效果 表单输入绑定示例代码效果展示 修饰符.lazy.number.trim 模板引用组件组成组件组成结构引入组件步骤style中的scoped作用 组件嵌套关系 Class绑定 绑定对象 绑定数…...

【AIGC】ChatGPT与人类理解力的共鸣:人机交互中的心智理论(ToM)探索
博客主页: [小ᶻZ࿆] 本文专栏: AIGC | ChatGPT 文章目录 💯前言💯心智理论(Theory of Mind,ToM)心智理论在心理学与神经科学中的重要性心智理论对理解同理心、道德判断和社交技能的重要性结论 💯乌得勒支大学研究对ChatGPT-4…...

代码训练营 day39|0-1背包问题,LeetCode 416
前言 这里记录一下陈菜菜的刷题记录,主要应对25秋招、春招 个人背景 211CS本CUHK计算机相关硕,一年车企软件开发经验 代码能力:有待提高 常用语言:C 系列文章目录 第九章 动态规划part03 文章目录 前言系列文章目录第九章 动态…...

LeetCode 203 - 移除链表元素
题目描述 给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val val 的节点,并返回 新的头节点 。 解题思路 创建一个虚拟头节点dummyHead,并将其next指向给定的头节点head,这样可以避免处理头节点的特…...

【海图界面上一些常见术语UTC、HDG、COG、SOG、LAT、LON的基本解释】
当然,以下是关于海图界面上一些常见术语UTC、HDG、COG、SOG、LAT、LON的基本解释: UTC (Coordinated Universal Time) 定义:UTC 是协调世界时(Coordinated Universal Time)的缩写,是一种与地球自转无关的…...

HL7协议简介及其在STM32上的解析实现
近期完成一个医疗相关的项目,其中包括了体征监测设备,该设备使用的通信协议便是HL7 V2.4 协议,在医疗信息化领域,HL7(Health Level Seven)协议扮演着至关重要的角色。它是一种国际标准,用于定义医疗机构间以及医疗设备与信息系统之间的数据交换格式和通信协议。HL7标准旨…...

TensorRT推理端到端
TensorRT推理端到端 1.参考链接2.宿主机上安装CUDA 12.4.13.安装nvidia-container-toolkit4.创建ghcr.io/intel/llvm/ubuntu2204_base容器5.容器内安装CUDA 12.4.1 + TensorRT10.1.06.安装依赖7.准备resnet50模型8.准备bert模型9.准备yolov5m模型10.编译TensorRT推理程序11.onn…...

获取历史的天气预报数据的网站
要获取从2019年到现在某个中国城市的天气数据,您可以通过以下方法实现: 1. 使用第三方天气数据API 许多天气服务提供商提供了历史天气数据的API接口,您可以通过这些API获取所需的数据。以下是一些常用的天气数据API提供商: 1.1…...

【VUE】Vue中常用的修饰符
事件修饰符 .stop:阻止事件冒泡。.prevent:阻止默认事件。.capture:使用事件捕获模式。.self:只当事件在该元素本身(比如不是子元素)触发时触发回调。.once:只触发一次事件。 按键修饰符 .en…...

数据分箱:如何确定分箱的最优数量?
选择最优分箱可以考虑以下几种方法: 一、基于业务理解 分析业务背景:从业务角度出发,某些特征可能有自然的分组或区间划分。例如,年龄可以根据不同的人生阶段进行分箱,收入可以根据常见的收入等级划分。 优点&#x…...

机器学习核心功能:分类、回归、聚类与降维
机器学习核心功能:分类、回归、聚类与降维 机器学习领域的基本功能类型通常按照学习模式、预测目标和算法适用性来分类。这些类型包括监督学习、无监督学习、半监督学习和强化学习,它们可以进一步细化为特定的任务,如分类、回归、聚类和降维…...

Python爬虫-eBay商品排名数据
前言 本文是该专栏的第39篇,后面会持续分享python爬虫干货知识,记得关注。 本文以eBay为例,通过搜索目标”关键词“,获取相关搜索”关键词“的商品排名数据。废话不多说,具体实现思路和详细逻辑,笔者将在正文结合完整代码进行详细介绍。接下来,跟着笔者直接往下看正文详…...
LabVIEW提高开发效率技巧----图像处理加速
在现代工业和科研中,图像处理技术被广泛应用于质量检测、自动化控制、机器人导航等领域。然而,随着图像数据量的增加,传统的CPU处理方式可能难以满足实时性和高效处理的需求。LabVIEW通过结合NI Vision模块和FPGA硬件平台,可以显著…...
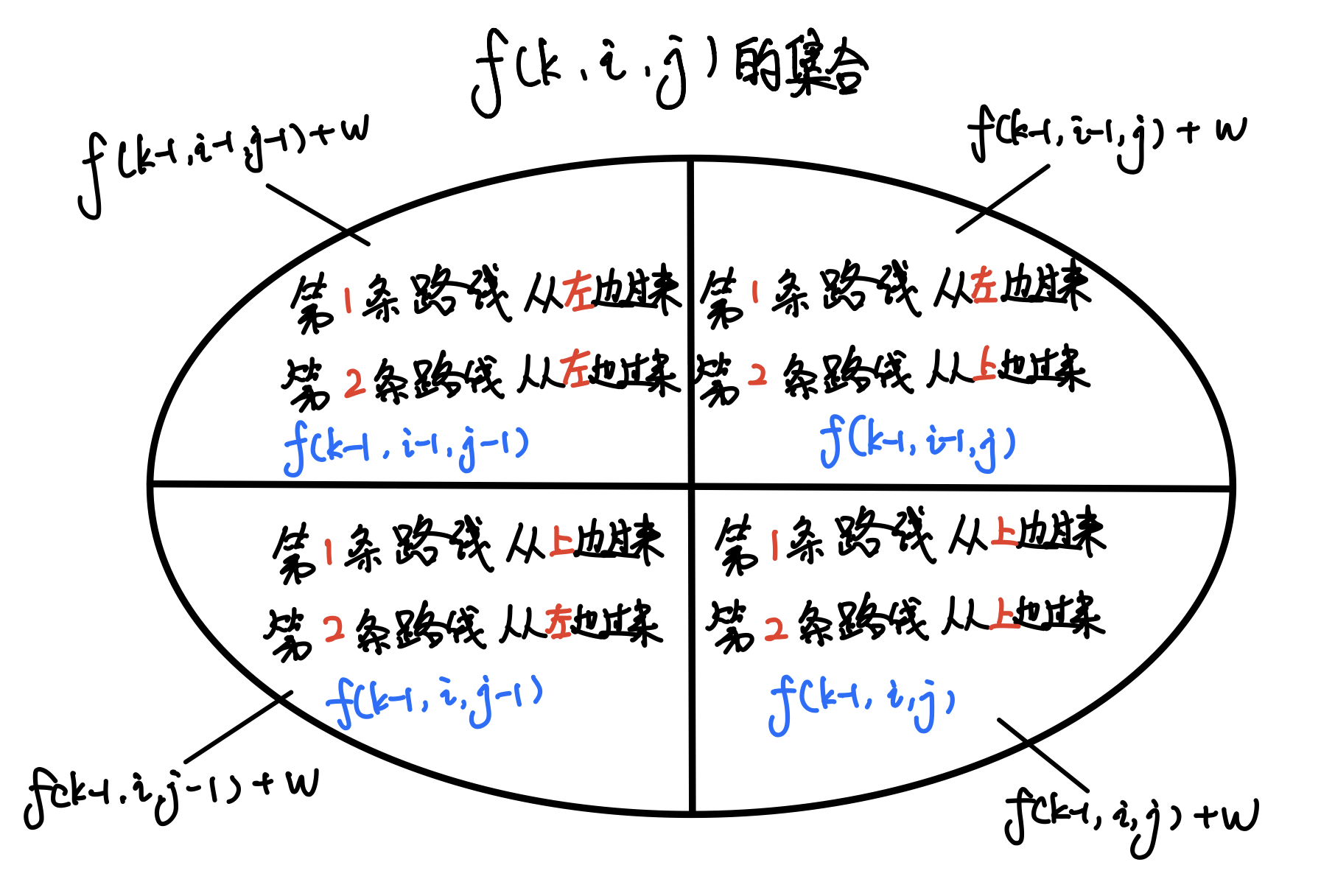
AcWing1027
题目重述: 题目的核心是找到一条路径的最大权值总和,但路径要从起点 (1, 1) 走到终点 (n, n)。由于两条路径分别经过不同的格子,我们可以巧妙地将问题简化为两次同时出发的路径问题。这种映射的设计让我们能够更方便地处理两条路径重叠在同一…...

23 Shell Script服务脚本
Linux 服务脚本 一、Linux 开机自动启动服务 linux开机服务原理: ①linux系统启动首先加载kernel ②初始操作系统 ③login验证程序等待用户登陆 初始化操作系统 kernel加载/sbin/init创建用户空间的第一个程序 该程序完成操作系统的初…...

三周精通FastAPI:3 查询参数
查询参数 FastAPI官网手册:https://fastapi.tiangolo.com/zh/tutorial/query-params/ 上节内容:https://skywalk.blog.csdn.net/article/details/143046422 声明的参数不是路径参数时,路径操作函数会把该参数自动解释为**查询**参数。 from…...

大语言模型学习指南:入门、应用与深入
0x00 学习路径概述 本文将学习路径划分为三个部分:入门篇、应用篇、深入篇。每个章节针对不同的学习需求,帮助你从基础知识入手,逐步掌握大语言模型(LLM)的使用、应用开发以及技术原理等内容。 学习目标 入门篇&…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...
