高中数学:立体几何-外接球的外心法
文章目录
- 一、外心法定义
- 二、习题
- 1、例题一
- 2、例题二
- 3、例题三
- 4、例题四
一、外心法定义
依然以三棱锥为例
即,找到三棱锥的外接球的球心,从而可以确定出外接球的半径R。
而三棱锥有四个顶点,这四个顶点必然都在外接球的球面上。
寻找思路:
找到底面外接圆的圆心,然后,过该圆心做垂线,那么,这个线上的点,到三个顶点的距离相等。
再找顶点到该垂线上的某个点的距离,使得该距离等于该点到底面顶点的距离。
此时,该点即为外接球的球心。
因为它到三棱锥的四个顶点的距离相等。
一般,我们把其中一个直角三角形作为底面,找它的外心。因为,直角三角形的外心必然在斜边上。

这种解法适合的题目,一般有个前提条件
1、可以找到一条线垂直某个面,那么,将该面作为底面。
可能用到的公式:
正弦定理

余弦定理

这两个定理,用于球三角形外接圆的半径。
二、习题
1、例题一

解析
我们发现,底面△ABC是一个直角三角形,所以,它的外心在斜边BC的中点。
然后,经过BC中点做垂线。
又发现面PBC⊥面ABC,所以,垂线必然在PBC平面内。
从而,变成找△PBC的外心。
由于,知道△PBC的三边长,于是,利用正弦定理和余弦定理,直接求出外接圆半径,即为三棱锥外接球的半径。

2、例题二

解析
从题目信息,可以发现△ABC是直角三角形,AC为斜边。取AC中点D。
在根据勾股定理,可以证明,PD⊥底面ABC
进而,三棱锥的外接球半径即为△PAC的外接圆半径

3、例题三

解析
发现△ACP是直角三角形,△ABP为等边三角形
在根据勾股定理,发现,△ACD也是直角三角形。
所以,AC⊥面ABP,于是,将△ABP作为底面求解。
注意,不要用Rt△ACP为底面,要用等边△ABP为底面找球心。

4、例题四

解析
以等边△BCD为底面,取BD中点T,则△ATC也是等边三角形。
所以,先找△BCD的外心,这个外心必然在CT直线上。
从而得解
为 2 13 3 \frac{2\sqrt{13}}{3} 3213
相关文章:

高中数学:立体几何-外接球的外心法
文章目录 一、外心法定义二、习题1、例题一2、例题二3、例题三4、例题四 一、外心法定义 依然以三棱锥为例 即,找到三棱锥的外接球的球心,从而可以确定出外接球的半径R。 而三棱锥有四个顶点,这四个顶点必然都在外接球的球面上。 寻找思路…...

【Python-AI篇】人工智能python基础-计算机组成原理
1. 计算机组成原理 2. python基础(查漏补缺) 2.1 字符串 2.1.1 字符串查找方法 find(): 检测某个字符串是否包含在这个字符串中,在的话返回下标,不在的话返回-1index(): 检测某个字符串是否包含在这个字…...

Java Exercise
3194. 最小元素和最大元素的最小平均值 Solution类 class Solution {public double minimumAverage(int[] nums){int n nums.length / 2;Arrays.sort(nums);int average 0;ArrayList<Double> arrayList new ArrayList<>();int i;int j;for (i 0, j nums.leng…...

滚雪球学Redis[9.1讲]:Redis的常见问题与最佳实践
全文目录: 前言1. Redis的常见问题排查常见错误信息与解决方案性能瓶颈的识别与处理数据一致性问题的排查 2. Redis的最佳实践Redis使用中的通用原则典型业务场景中的最佳实践如何避免Redis中的反模式 小结下期预告 前言 在上一章【第八章:Redis的扩展与…...

python获取当前鼠标位置的RGB值
效果 依赖 pip install Pillow pyautoguisudo apt install gnome-screenshot代码 import pyautogui import timedef get_rgb_at_mouse():try:while True:# 获取当前鼠标的位置x, y pyautogui.position()# 截取当前屏幕图像screenshot pyautogui.screenshot()# 获取鼠标位置…...

Ubuntu20.04运行深蓝运动规划hw_5
前言 环境: ubuntu 20.04 ; ROS版本: noetic; 问题 运行 roslaunch waypoint_trajectory_generator test.launch 出现如下错误 Invalid argument "/map" passed to canTransform argument source_frame in tf2 fra…...

删除node_modules文件夹
前言 当安装了较多模块后,node_modules目录下的文件会很多,直接删除整个目录会很慢,下面介绍些快速删除node_modules目录的方法。 方法一:使用rimraf模块的命令 在全局安装rimraf模块,然后通过其命令来快速删除node…...

基于Springboot+Vue的民宿管理系统(含源码数据库)
1.开发环境 开发系统:Windows10/11 架构模式:MVC/前后端分离 JDK版本: Java JDK1.8 开发工具:IDEA 数据库版本: mysql5.7或8.0 数据库可视化工具: navicat 服务器: SpringBoot自带 apache tomcat 主要技术: Java,Springboot,mybatis,mysql,vue 2.视频演示地址 3.功能 在这个…...
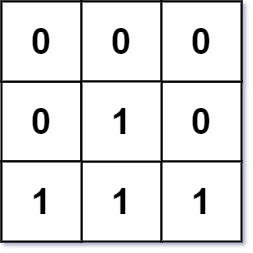
[LeetCode] 542. 01矩阵
题目描述: 给定一个由 0 和 1 组成的矩阵 mat ,请输出一个大小相同的矩阵,其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。 两个相邻元素间的距离为 1 。 示例 1: 输入:mat [[0,0,0],[0,1,0],[0,0,0]] 输出…...

国产AI模型“Yi-Lightning”逆袭超越GPT-4!
近日,全球千万用户盲测投票产生的AI模型排行榜公布,令人惊喜的是,国产AI模型“Yi-Lightning”成功逆袭,一举超越了此前长期占据榜首的GPT-4。 Ai 智能办公利器 - Ai-321.com 人工智能 - Ai工具集 - 全球热门人工智能软件ai工具集…...

安卓設備上怎麼設置HTTP代理?
HTTP代理是一種仲介伺服器,它在用戶的設備和互聯網之間傳遞請求。通過HTTP代理,請求會先發送到代理伺服器,然後由代理伺服器轉發到目標網站。這樣,目標網站只會看到代理伺服器的IP地址,而不是真實IP地址。這種機制可以…...

学习Redisson实现分布式锁
官网:https://redisson.org/ 官方文档:https://redisson.org/docs/getting-started/ 官方中文文档:https://github.com/redisson/redisson/wiki/%E7%9B%AE%E5%BD%95 1、引入依赖 <!--redisson--> <dependency><groupId>or…...

2024CSP-J模拟赛9————S12678
一,赛中得分 T1100T2100T350T440总分290 二,赛中概括 T1T2较快过,T3T4骗了90分(意料之中,这么好骗分!!!)。 三,题目解析 涂格子(paint) 问题描述 现在有…...

HarmonyOS中ArkUi框架中常用的装饰器
目录 1.装饰器 1)Component 1--装饰内容 2)Entry 1--装饰内容 2--使用说明 3)Preview 1--装饰内容 2--使用说明 4)CustomDialog 1--装饰内容 2--使用说明 5)Observed 1--装饰内容 2--使用说明 6)ObjectLin…...

服务攻防之Redis数据库安全
最近我将会把一些服务攻防方面的姿势在这里做一个简单总结。欢迎大家留言讨论。 首先我们先对这类安全问题做一个总体的概括! 一、总概 1.服务判断: 端口扫描:利用服务开启后的目标端口开放判断 组合判断:利用搭建常见组合分析可能开放服务…...

随机森林算法的原理与实现
随机森林(Random Forest)是一种集成学习算法,它通过构建多个决策树并结合这些树的结果来进行分类或回归。与单一的决策树相比,随机森林通过集成多个树的结果,能够显著提高预测的准确性和稳定性,减少模型的过…...

模仿百度-基础版
<!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>百度案例</title><style>*{margin: 0;p…...

c++贴瓷砖
题目描述 有一块大小是 2 * n 的墙面,现在需要用2种规格的瓷砖铺满,瓷砖规格分别是 2 * 1 和 2 * 2,请计算一共有多少种铺设的方法。 输入 输入的第一行包含一个正整数T(T<20),表示一共有T组数据&…...
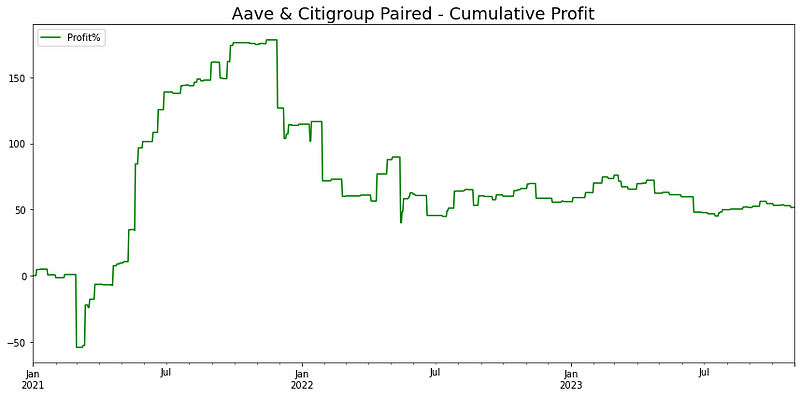
用 Python 构建高级配对交易策略
作者:老余捞鱼 原创不易,转载请标明出处及原作者。 写在前面的话: 本文阐述通过分析加密货币和传统金融工具之间的相关性和协整性,以及实施 Z-score 方法来生成交易信号,然后介绍如何使用 Python 构建配对交易策…...

Java 引用数据类型详解、字符串的不可变性、如何处理字符串的内存管理、String Pool 及其优化
文章目录 1. 引用数据类型1.1 常见引用数据类型 2. 字符串的不可变性2.1 不可变性的优点2.2 不可变性示例 3. 如何处理字符串的内存管理3.1 String Pool3.2 String 内存优化 4. String Pool 及其优化4.1 String Pool的工作原理4.2 String Pool的优化4.3 使用 intern() 进一步优…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...

UE5 音效系统
一.音效管理 音乐一般都是WAV,创建一个背景音乐类SoudClass,一个音效类SoundClass。所有的音乐都分为这两个类。再创建一个总音乐类,将上述两个作为它的子类。 接着我们创建一个音乐混合类SoundMix,将上述三个类翻入其中,通过它管理每个音乐…...

CSS 工具对比:UnoCSS vs Tailwind CSS,谁是你的菜?
在现代前端开发中,Utility-First (功能优先) CSS 框架已经成为主流。其中,Tailwind CSS 无疑是市场的领导者和标杆。然而,一个名为 UnoCSS 的新星正以其惊人的性能和极致的灵活性迅速崛起。 这篇文章将深入探讨这两款工具的核心理念、技术差…...
