c++ 散列表
散列表(Hash Table)是一种高效的数据结构,广泛用于实现快速的键值对存储。
基本概念
散列表使用哈希函数将键映射到数组的索引。其主要优点在于平均情况下提供常数时间复杂度的查找、插入和删除操作。
- 哈希函数: 将键映射到一个固定大小的数组索引。一个好的哈希函数应该具备:
- 散列均匀性:不同的键应该尽量映射到不同的索引。
- 计算简单:哈希值的计算应该高效。
冲突处理
由于多个键可能映射到同一个索引,必须采取措施处理冲突。常见的冲突解决方法包括:
- 链地址法: 在每个数组索引处使用链表存储所有映射到该索引的键值对。
- 开放寻址法: 在数组中查找下一个可用位置,例如线性探测、二次探测和双重散列等方法。
性能分析
时间复杂度:
- 查找:O(1)(平均情况),O(n)(最坏情况,发生冲突时)
- 插入:O(1)(平均情况),O(n)(最坏情况)
- 删除:O(1)(平均情况),O(n)(最坏情况)
空间复杂度: O(n),即存储元素的数量。
负载因子(Load Factor): 定义为元素数量与表大小的比率。一般在负载因子超过一定阈值(如0.7)时进行扩容,以保持性能。
代码实现
链地址法
#include <iostream>
#include <vector>
#include <list>
#include <utility> // for std::pair
#include <functional> // for std::hashtemplate <typename Key, typename Value>
class HashTable {
public:HashTable(size_t size = 10) : table(size), current_size(0) {}void Insert(const Key& key, const Value& value) {size_t index = Hash_(key) % table.size();for (auto& pair : table[index]) {if (pair.first == key) {pair.second = value; // 更新值return;}}table[index].emplace_back(key, value); // 插入新键值对current_size++;if (current_size > table.size() * load_factor) {Resize_();}}bool Get(const Key& key, Value& value) const {size_t index = Hash_(key) % table.size();for (const auto& pair : table[index]) {if (pair.first == key) {value = pair.second;return true;}}return false; // 未找到}bool Remove(const Key& key) {size_t index = Hash_(key) % table.size();auto& cell = table[index];for (auto it = cell.begin(); it != cell.end(); ++it) {if (it->first == key) {cell.erase(it); // 删除current_size--;return true;}}return false; // 未找到}private:std::vector<std::list<std::pair<Key, Value>>> table; // 哈希表的数组size_t current_size; // 当前存储的元素数量const float load_factor = 0.7; // 负载因子size_t Hash_(const Key& key) const {return std::hash<Key>()(key); // 使用标准哈希函数}void Resize_() {std::vector<std::list<std::pair<Key, Value>>> old_table = table;table.resize(old_table.size() * 2); // 扩容current_size = 0;for (const auto& cell : old_table) {for (const auto& pair : cell) {Insert(pair.first, pair.second); // 重新插入}}}
};int main() {HashTable<std::string, int> hash_table;hash_table.Insert("apple", 1);hash_table.Insert("banana", 2);int value;if (hash_table.Get("apple", value)) {std::cout << "apple: " << value << std::endl; // 输出: apple: 1}hash_table.Remove("apple");if (!hash_table.Get("apple", value)) {std::cout << "apple not found" << std::endl; // 输出: apple not found}return 0;
}
代码解析
- 数据结构:
- 使用
std::vector存储链表,链表用于处理冲突。 - 每个链表中的元素是
std::pair<Key, Value>,用于存储键值对。
- 使用
- 插入操作:
- 计算哈希值并确定索引。
- 检查索引处是否存在相同的键,如果存在则更新值,否则插入新键值对。
- 如果当前元素个数超过负载因子,则调用
Resize扩容。
- 查找操作:
- 计算索引,遍历链表查找对应的键。
- 删除操作:
- 计算索引并在链表中查找键,找到后删除。
- 扩容:
- 创建新的、更大的表,重新插入旧表中的元素以保证均匀分布。
开放寻址法
#include <iostream>
#include <vector>
#include <utility> // for std::pair
#include <stdexcept> // for std::out_of_rangetemplate <typename Key, typename Value>
class HashTable {
public:HashTable(size_t size = 10) : table(size), current_size(0), load_factor(0.7) {}void Insert(const Key& key, const Value& value) {if (current_size >= table.size() * load_factor) {Resize_();}size_t index = Hash_(key) % table.size();while (table[index].first != Key() && table[index].first != key) {index = (index + 1) % table.size(); // 线性探测}table[index] = { key, value };current_size++;}bool Get(const Key& key, Value& value) const {size_t index = Hash_(key) % table.size();while (table[index].first != Key()) {if (table[index].first == key) {value = table[index].second;return true;}index = (index + 1) % table.size(); // 线性探测}return false; // 未找到}bool Remove(const Key& key) {size_t index = Hash_(key) % table.size();while (table[index].first != Key()) {if (table[index].first == key) {table[index] = { Key(), Value() }; // 标记为删除current_size--;return true;}index = (index + 1) % table.size(); // 线性探测}return false; // 未找到}private:std::vector<std::pair<Key, Value>> table; // 散列表的数组size_t current_size; // 当前存储的元素数量const float load_factor; // 负载因子size_t Hash_(const Key& key) const {return std::hash<Key>()(key); // 使用标准哈希函数}void Resize_() {std::vector<std::pair<Key, Value>> old_table = table;table.resize(old_table.size() * 2, { Key(), Value() }); // 扩容current_size = 0;for (const auto& pair : old_table) {if (pair.first != Key()) {Insert(pair.first, pair.second); // 重新插入}}}
};int main() {HashTable<std::string, int> hash_table;hash_table.Insert("apple", 1);hash_table.Insert("banana", 2);int value;if (hash_table.Get("apple", value)) {std::cout << "apple: " << value << std::endl; // 输出: apple: 1}hash_table.Remove("apple");if (!hash_table.Get("apple", value)) {std::cout << "apple not found" << std::endl; // 输出: apple not found}return 0;
}
代码解析
- 数据结构:
- 使用
std::vector<std::pair<Key, Value>>存储键值对。未使用的槽位初始化为Key()和Value(),用于标记空槽。
- 使用
- 插入操作:
- 计算哈希值并确定初始索引。
- 如果发生冲突,使用线性探测法查找下一个可用的索引。
- 如果当前元素数量超过负载因子,则调用
Resize方法进行扩容。
- 查找操作:
- 计算索引并线性探测,直到找到对应的键或到达空槽。
- 删除操作:
- 在查找过程中,如果找到目标键,则标记该位置为已删除。
- 扩容:
- 创建一个更大的数组并重新插入旧表中的元素,以保持均匀分布。
总结
散列表是一种高效且灵活的数据结构,适合用于需要快速查找和存储的场景。通过合理设计哈希函数和冲突处理策略,可以实现良好的性能。
相关文章:

c++ 散列表
散列表(Hash Table)是一种高效的数据结构,广泛用于实现快速的键值对存储。 基本概念 散列表使用哈希函数将键映射到数组的索引。其主要优点在于平均情况下提供常数时间复杂度的查找、插入和删除操作。 哈希函数: 将键映射到一个固定大小的…...

Windows通过netsh控制安全中心防火墙和网络保护策略
Windows通过netsh控制安全中心防火墙和网络保护策略 1. 工具简介 【1】. Windows安全中心 【2】. netsh工具 netsh(Network Shell) 是一个Windows系统本身提供的功能强大的网络配置命令行工具。 2. 开启/关闭防火墙策略 在设置端口(禁用/启用)前&am…...
)
UML(Unified Modeling Language,统一建模语言)
UML(Unified Modeling Language,统一建模语言)是一种标准化的图形化语言,用于软件工程中的可视化建模。UML由Grady Booch、James Rumbaugh和Ivar Jacobson共同开发,他们各自的工作(Booch方法、OMT方法和OOS…...

深⼊理解指针(2)
目录 1. 数组名的理解 2. 使⽤指针访问数组 3. ⼀维数组传参的本质 4. ⼆级指针 5. 指针数组 6. 指针数组模拟⼆维数组 1. 数组名的理解 我们在使⽤指针访问数组的内容时,有这样的代码: int arr[10] {1,2,3,4,5,6,7,8,9,10}; int *p &arr[…...

Ubuntu中MySQL远程登录设置
mysql单独放在一台Ubuntu服务器上,我远程连接不上。可能是安装的时候忘记设置远程登录了。事后补救措施如下: MySQL 绑定地址配置问题 MySQL 可能只绑定了 localhost,无法接受来自外部主机的连接。你需要检查 MySQL 的配置文件 /etc/mysql/…...

typescript 中封装一个 class 来解析接口响应数据
在TypeScript中,封装一个类来解析接口响应数据是一个常见的做法,它允许你将与接口响应相关的逻辑封装在一个可复用的单元中。下面是一个示例,展示了如何定义一个TypeScript类来解析一个假设的API接口响应数据。 首先,我们定义一个…...
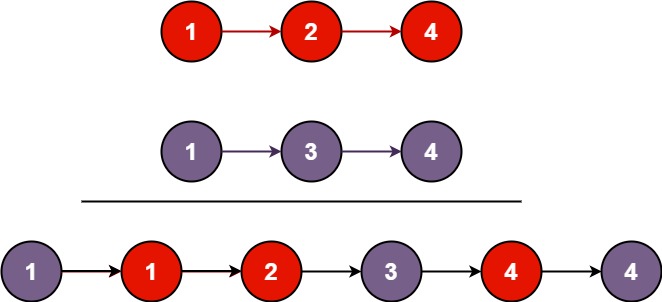
[LeetCode] 21. 合并两个有序链表
题目描述: 将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。 示例 1: 输入:l1 [1,2,4], l2 [1,3,4] 输出:[1,1,2,3,4,4]示例 2: 输入:l1 [], l2 […...
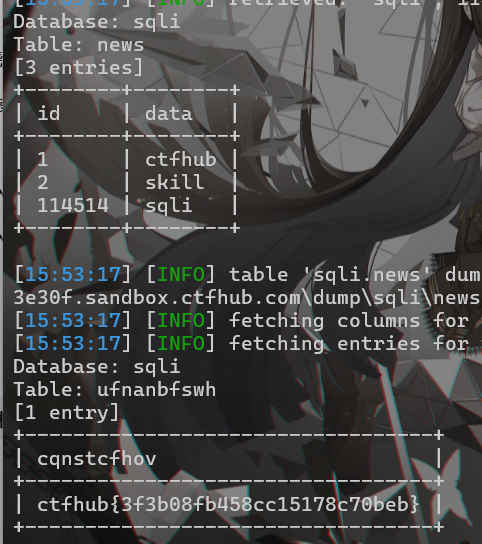
CTFHUB技能树之SQL——MySQL结构
开启靶场,打开链接: 先判断一下是哪种类型的SQL注入: 1 and 11# 正常回显 1 and 12# 回显错误,说明是整数型注入 判断一下字段数: 1 order by 2# 正常回显 1 order by 3# 回显错误,说明字段数是2列 知道…...

Git小知识:合理的分支命名约定
前言:创建新分支时,对 Git 分支进行合理的命名非常重要,应选择有描述性的名称,因为它可以帮助团队成员更好地理解分支的目的和内容,以便将来回顾时能立即明白分支的目的。以下是一些常见的分支命名约定: 功…...

Ubuntu如何显示pcl版本
终端输入: apt-cache show libpcl-dev可以看到,Ubuntu20.04,下载的pcl,应该都是1.10版本的...

wordcloud 字体报错
wordcloud 字体报错 词云库报错:Only supported for TrueType fonts字体文件问题pillow版本的问题wordcloud版本问题(我的最终解决方案) 词云库报错:Only supported for TrueType fonts 字体文件问题 解决方法 写绝对路径 &…...

使用Matplotlib绘制极轴散点图
散点图对于理解数据可视化中变量之间的相互作用至关重要。虽然散点图经常在笛卡尔坐标中创建,但我们也可以使用Matplotlib在极轴上创建散点图。有了这个功能,人们可以以创新的方式查看圆形或角形数据,例如周期性趋势或定向模式。在本文中&…...

Elasticsearch入门:增删改查详解与实用场景
引言 在我之前做社交架构设计的时候,我们有一项关键且必要的需求:需要存储并记录用户的所有聊天记录。这些记录不仅用于业务需求,也承担了风控审查的职责。因此,在架构设计中,我们需要考虑每天海量的聊天消息量&#…...

【AI论文精读6】SELF-RAG(23.10)附录
【AI论文解读】【AI知识点】【AI小项目】【AI战略思考】 P1,P2,P3 附录 A SELF-RAG 细节 A.1 反思标记(reflection tokens) 反思标记的定义 下面我们提供了反思标记类型和输出标记的详细定义。前三个方面将在每个片段…...

sql-labs靶场第十七关测试报告
目录 一、测试环境 1、系统环境 2、使用工具/软件 二、测试目的 三、操作过程 1、寻找注入点 2、注入数据库 ①寻找注入方法 ②爆库,查看数据库名称 ③爆表,查看security库的所有表 ④爆列,查看users表的所有列 ⑤成功获取用户名…...

面试官:MySQL一次到底插入多少条数据合适啊?
前言 大家好!在互联网时代,我们的每一个动作,无论是浏览网页、分享动态、点赞、购物或者搜索信息,都会在背后产生数据。这些数据,根据其用途和重要性,可能会被储存到不同的地方,其中最常见的存…...
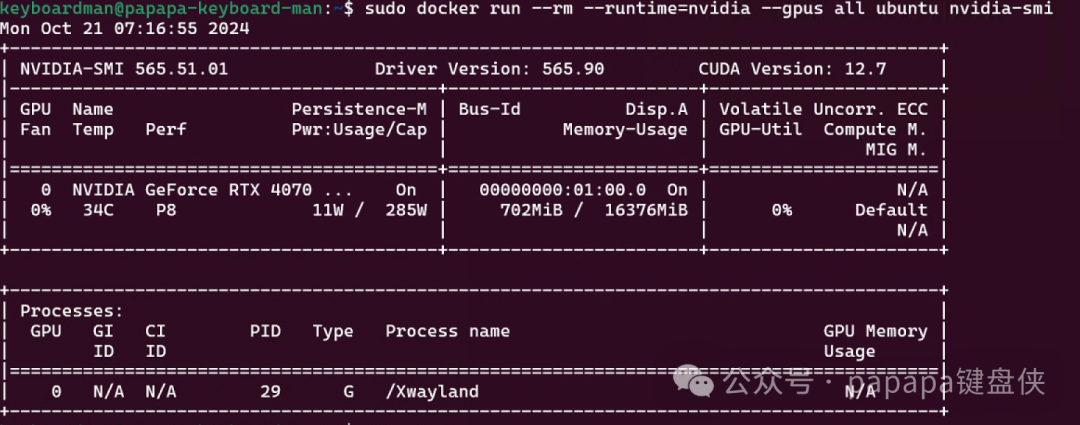
WSL2 构建Ubuntu系统-轻量级AI运行环境
环境:Win11 软件:WSL2 安装环境:Ubuntu 22.04 检查电脑是否开启虚拟化 打开:任务管理器->性能->CPU CPU 开启虚拟化(通常默认是开启的,如果没有开启需要BIOS开启) 虚拟化设置࿰…...

什么是凸二次规划问题
我们从凸二次规划的基本概念出发,然后解释它与支持向量机的关系。 一、凸二次规划问题的详细介绍 凸二次规划问题是优化问题的一类,目标是最小化一个凸的二次函数,受一组线性约束的限制。凸二次规划是一类特殊的二次规划问题,其…...

解决 Elasticsearch cluster_block_exception 错误的终极指南
Elasticsearch 是一个功能强大的分布式搜索引擎,广泛应用于全文检索、实时分析等场景。 尽管如此,像任何复杂系统一样,它也会遇到一些运行问题,其中较为常见且影响较大的就是 cluster_block_exception 错误。 本文将深入解析这种错…...

QT sql驱动错误QMYSQL driver not loaded
引用文章QMYSQL driver not loaded 根据引用文章,到在编译QT mysql.pro的源码步骤时,构建没有报错,但是在对应的文件夹内没有找到编译好的dll文件,经过全电脑搜寻,找到在此文件夹内。 遇到同样错误的朋友可以找找QT安…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...
