【Petri网导论学习笔记】Petri网导论入门学习(七) —— 1.5 并发与冲突
导航
- 1.5 并发与冲突
- 1.5.1 并发
- 定义 1.14
- 定义 1.15
- 1.5.2 冲突
- 定义 1.17
- 1.5.3 一般Petri网系统中的并发与冲突
- 定义 1.18
- 一般网系统中无冲撞概念
- 阻塞(有容量函数K的P/T系统,类似于冲撞)
- 一般Petri网中并发与冲突共存情况
1.5 并发与冲突
Petri网的一大突出优点就是便于描述并发与冲突,其中同步与并发的概念紧密相连
以下从基本网系统入手进行讨论
1.5.1 并发
考察图 1.15 的基本网系统 Σ 1 = ( B , E ; F , c 0 ) \Sigma_1=(B,E;F,c_0) Σ1=(B,E;F,c0) ,其中 c 0 = { b 1 , b 2 } c_0=\{b_1,b_2\} c0={b1,b2}。在情态 c 0 c_0 c0下事件 e 2 e_2 e2和 e 3 e_3 e3都有权发生。这是因为
∙ e 2 = { b 1 } ⊆ c 0 且 e 2 ∙ ∩ c 0 = { b 3 } ∩ { b 1 , b 2 } = ∅ ∙ e 3 = { b 2 } ⊆ c 0 且 e 3 ∙ ∩ c 0 = { b 4 } ∩ { b 1 , b 2 } = ∅ ^\bullet e_2=\{b_1\}\subseteq c_0\:\text{且}\quad e_2^\bullet\cap c_0=\{b_3\}\cap\{\:b_1,b_2\:\}=\emptyset\\^\bullet e_3=\{b_2\}\subseteq c_0\:\text{且}\quad e_3^\bullet\cap c_0=\{b_4\}\cap\{\:b_1,b_2\:\}=\emptyset ∙e2={b1}⊆c0且e2∙∩c0={b3}∩{b1,b2}=∅∙e3={b2}⊆c0且e3∙∩c0={b4}∩{b1,b2}=∅
e 2 e_2 e2前集 b 1 b_1 b1是 c 0 c_0 c0且 e 2 e_2 e2后集与 c 0 c_0 c0有交集 b 3 b_3 b3且不是 b 1 b_1 b1与 b 2 b_2 b2
下面同理
假设 e 2 e_2 e2在情态 c 0 c_0 c0发生,变成新的情态 c 1 = { b 2 , b 3 } c_1=\{b_2,b_3\} c1={b2,b3},易知 e 3 e_3 e3在情态 c 1 c_1 c1仍有发生权。反之,如果 e 3 e_3 e3在情态 c 0 c_0 c0发生,得到新的情态 c 2 = { b 1 , b 4 } c_2=\{b_1,b_4\} c2={b1,b4},则 e 2 e_2 e2在情态 c 2 c_2 c2也仍有发生权。我们说 e 2 e_2 e2和 e 3 e_3 e3在情态 c 0 c_0 c0处于并发关系。
一般地说,如果两个事件在某情态下都有发生权,而且其中任何一个的发生都不会使另一个失去发生权,则称这两个事件在该情态下处于并发。

定义 1.14
设 Σ = ( B , E ; F , c 0 ) \Sigma=(B,E;F,c_0) Σ=(B,E;F,c0) 为一个EN 系统, e 1 , e 2 ∈ E , c e_1,e_2\in E,c e1,e2∈E,c 是 Σ \Sigma Σ 的一个情态。
如果
1 ) c [ e 1 > ∧ c [ e 2 > 2 ) c [ e 1 > c 1 → c 1 [ e 2 > ∧ c [ e 2 > c 2 → c 2 [ e 1 > \begin{aligned}&1)c[e_{1}>\wedge c[e_{2}>\\&2)c[e_{1}>c_{1}\to c_{1}[e_{2}>\wedge c[e_{2}>c_{2}\to c_{2}[e_{1}>\\\end{aligned} 1)c[e1>∧c[e2>2)c[e1>c1→c1[e2>∧c[e2>c2→c2[e1>
e 1 e_1 e1与 e 2 e_2 e2在情态 c c c上有发生权
e 1 e_1 e1发生后的情态可以继续发生 e 2 e_2 e2且 e 2 e_2 e2发生后的情态可以继续发生 e 1 e_1 e1
则称 e 1 e_1 e1和 e 2 e_2 e2在情态 c c c并发 , 或者说 e 1 e_1 e1和 e 2 e_2 e2在情态 c c c有一步发生权,记作 c [ { e 1 , e 2 } > 。 c[\{e_1,e_2\}>。 c[{e1,e2}>。
并发不能简单地理解为“同时发生”,而是指事件之间因果上的无依赖性。按网论的观点 , 事件(变迁)的发生只依赖于它们的外延 , 而与全局情况无关。在图1.15 的基本网系统中,事件 e 2 e_2 e2的外延是
∙ e 2 ∪ e 2 ∙ = { b 1 , b 3 } ^\bullet e_2\cup e_2^\bullet=\{\:b_1,b_3\:\} ∙e2∪e2∙={b1,b3}
事件 e 3 e_3 e3的外延是
∙ e 3 ∪ e 3 ∙ = { b 2 , b 4 } ^\bullet {e_3\cup e_3^\bullet}=\{\:b_2,b_4\:\} ∙e3∪e3∙={b2,b4}
由于 e 2 e_2 e2和 e 3 e_3 e3的外延之间没有公共部分,所以它们是两个互相独立的事件。这是基本网系统中两个事件处于并发的必要条件。
现在考察一下 e 2 e_{2} e2和 e 4 e_{4} e4两个事件之间的关系。前面已指出,在情态 c 0 = { b 1 , b 2 } c_0=\{b_1,b_2\} c0={b1,b2}下 e 2 e_{2} e2有发生权,但 e 4 e_4 e4在 c 0 c_0 c0没有发生权。如果 e 2 e_2 e2在 c 0 c_0 c0发生,得到情态 c 1 = { b 2 , b 3 } c_1=\{b_2,b_3\} c1={b2,b3},易知 e 4 e_{4} e4在 c 1 c_1 c1有发生权。也就是说, e 4 e_4 e4的发生权是通过 e 2 e_2 e2 (在 c 0 c_0 c0)发生获得的。我们说 e 2 e_2 e2和 e 4 e_4 e4的发生是一种顺序关系。
定义 1.15
设 ( B , E ; F , c 0 ) (B,E;F,c_0) (B,E;F,c0)为一个EN系统, e i , e j ∈ E e_i,e_j\in E ei,ej∈E, c c c是 Σ \Sigma Σ 的一个情态。如果
1 ) c [ e i > 但 ¬ c [ e j > 2 ) c [ e i > c ′ → c ′ [ e j > \begin{aligned}&1)c[e_{i}>\text{ 但 }\neg c[e_{j}>\\&2)c[e_{i}>c^{\prime}\to c^{\prime}[e_{j}>\\&\end{aligned} 1)c[ei> 但 ¬c[ej>2)c[ei>c′→c′[ej>
则称事件 e i e_i ei 和 e j e_j ej有顺序关系(sequential relation)。
在情态 c c c当中, e i e_i ei可以发生但是 e j e_j ej不能发生,
但是 e i e_i ei发生之后 e j e_j ej可以发生,所以称为有顺序关系。
下面继续考察并发关系的一些性质。前面已经指出,在图1.15 的 EN 系统中,事件 e 2 e_2 e2和 e 3 e_3 e3在 c 0 = { b 1 , b 3 } c_0=\{b_1,b_3\} c0={b1,b3}并发。如果这时 e 2 e_2 e2发生,得到情态 c 1 = { b 2 , b 3 } c_1=\{b_2,b_3\} c1={b2,b3}。分析一下易知,事件 e 3 e_{3} e3和 e 4 e_4 e4在 c 1 c_1 c1处于并发关系。这就是说,在该 EN 系统中,既存在情态 c 0 c_0 c0使 e 2 e_2 e2和 e 3 e_3 e3处于并发关系,也存在情态 c 1 c_1 c1使 e 3 e_3 e3和 e 4 e_4 e4处于并发关系。然而,在该系统的任意情态下, e 2 e_{2} e2和 e 4 e_{4} e4都不可能处于并发关系。这说明,并发关系没有传递性。
如果在情态 c 0 c_0 c0发生事件 e 3 e_3 e3,得到情态 c 2 = { b 1 , b 4 } c_2=\{b_1,b_4\} c2={b1,b4},易知事件 e 2 e_2 e2和 e 5 e_5 e5在 c 2 c_2 c2也处于并发关系。不难看出,这个EN 系统还存在情态 c 3 = { b 3 , b 4 } c_3=\{b_3,b_4\} c3={b3,b4}使得 e 4 e_{4} e4和 e 5 e_{5} e5在 c 3 c_{3} c3并发。也就是说,在这个系统中,事件对 e 2 e_2 e2 和 e 3 , e 3 e_3,e_3 e3,e3 和 e 4 , e 2 e_4,e_2 e4,e2 和 e 5 e_5 e5 以及 e 4 e_4 e4 和 e 5 e_5 e5,都有可能处于并发关系。然而,在事件 e 2 e_{2} e2和 e 4 e_{4} e4之间以及 e 3 e_{3} e3和 e 5 e_{5} e5之间,都是一种顺序关系。在这种情况下,我们也可以说,事件串(序列) e 2 e 4 e_2e_4 e2e4和事件串 e 3 e 5 e_3e_5 e3e5在情态 c 0 c_0 c0处于并发。
假如从情态 c 0 c_0 c0 发生事件串 e 2 e 4 e_2e_4 e2e4,得到的情态为 { b 2 , b 5 } \{b_2,b_5\} {b2,b5}。这时只有等待事件串 e 3 e 5 e_3e_5 e3e5 发生后,事件 e 6 e_{6} e6才有发生权。反之,如果从 c 0 c_0 c0发生事件串 e 3 e 5 e_3e_5 e3e5,得到情态 { b 1 , b 6 } \{b_1,b_6\} {b1,b6}。这时也要等待另一事件串 e 2 e 4 e_2e_4 e2e4 发生后,事件 e 6 e_6 e6才有发生权。可见,事件 e 6 e_6 e6起到了使两个并发的事件串 e 2 e 4 e_2e_4 e2e4和 e 3 e 5 e_3e_5 e3e5同步的作用。同步(synchronous)的概念是同并发关系紧密相联的。它也是并发系统中的一个重要概念。
1.5.2 冲突
考察图 1.16 的基本网系统 Σ 2 = ( B , E ; F , c 0 ) \Sigma_2=(B,E;F,c_0) Σ2=(B,E;F,c0) ,其中 c 0 = { b 2 } c_0=\{b_2\} c0={b2}。事件 e 1 e_1 e1和 e 3 e_3 e3在情态 c 0 c_0 c0都可能发生。但如果 e 1 e_1 e1发生,产生新的情态 c 1 = { b 1 } c_1=\{b_1\} c1={b1}, e 3 e_3 e3在 c 1 c_1 c1失去了发生权。反过来也是这样,如果在情态 c 0 c_0 c0下 e 3 e_3 e3发生,得到新的情态 c 2 = { b 3 } c_2=\{b_3\} c2={b3}, e 1 e_1 e1在情态 c 2 c_2 c2失去了发生权。这种情况称为冲突。
因为只能选一个变迁发生,所以 e 1 e_1 e1与 e 3 e_3 e3不能同时发生。

e 2 和 e 4 的发生是一种顺序关系。 定义 1.15 设 ( B , E ; F , c 0 ) 为一个 EN 系统, e i , e j ∈ E , c 是 Σ 的一个情态。如果 1) c [ e i > 但 ¬ c [ e j > ( 1.38 ) 2) c [ e i > c ′ → c ′ [ e j > ( 1.39 ) \begin{aligned}&e_{2}\text{ 和 }e_{4}\text{ 的发生是一种顺序关系。}\\&\text{定义 1.15 设 }(B,E;F,c_0)\text{ 为一个 EN 系统,}e_i,e_j\in E\text{,}c\text{ 是 }\Sigma\text{ 的一个情态。如果}\\&\text{1)}c[e_{i}>\text{ 但 }\neg c[e_{j}>&&(1.38)\\&\text{2)}c[e_{i}>c^{\prime}\to c^{\prime}[e_{j}>&&(1.39)\end{aligned} e2 和 e4 的发生是一种顺序关系。定义 1.15 设 (B,E;F,c0) 为一个 EN 系统,ei,ej∈E,c 是 Σ 的一个情态。如果1)c[ei> 但 ¬c[ej>2)c[ei>c′→c′[ej>(1.38)(1.39)
则称事件 e 1 e_1 e1和 e 2 e_2 e2在情态 c c c处于冲突关系。
e 1 e_1 e1与 e 2 e_2 e2在情态 c c c上有发生权
e 1 e_1 e1发生后的情态可以继续发生 e 2 e_2 e2且 e 2 e_2 e2发生后的情态可以继续发生 e 1 e_1 e1
在图 1.16 的这种 EN 系统中, e 1 e_1 e1 和 e 3 e_3 e3在 c 0 c_0 c0 冲突,是因为 c 0 ⊇ ∙ e 1 ∪ ∙ e 3 c_0\supseteq^\bullet e_1\cup^\bullet e_3 c0⊇∙e1∪∙e3 而且 ∙ e 1 ∩ ^\bullet e_1\cap ∙e1∩ ∙ e 3 ≠ ∅ ^{\bullet}e_3\neq\emptyset ∙e3=∅。下面考察另一种类型的例子。在图 1.17a)的基本网系统 Σ 3 \Sigma_{3} Σ3中,在情态 c = c= c= { b 1 , b 2 } \{b_1,b_2\} {b1,b2}下,事件 e 1 e_1 e1和 e 2 e_2 e2都是可以发生的。然而它们当中只能有一个发生,同时,其中的任一事件发生,都会使另一个失去发生权。因此 e 1 e_1 e1 和 e 2 e_2 e2 在情态 { b 1 , b 2 } \{b_1,b_2\} {b1,b2} 也处于冲突。然而,这种冲突同图 1.16 的 EN 系统 Σ 2 \Sigma_{2} Σ2中的冲突又有不同之处。在 Σ 3 \Sigma_3 Σ3中,“ e 1 ∩ e_1\cap e1∩ ∙ e 2 = ∅ ^{\bullet}e_2=\emptyset ∙e2=∅,但 e 1 ∙ ∩ e 2 ∙ ≠ ∅ e_1^\bullet\cap e_2^\bullet\neq\emptyset e1∙∩e2∙=∅,所以当其中一个事件如 e 1 e_1 e1发生后, e 2 e_2 e2失去发生权的原因不是 ∙ e 2 ^{\bullet}e_2 ∙e2不满足条件,而在于 e 2 ∙ e_2^\bullet e2∙不满足条件。即 c [ e 1 > c 1 → c 1 ∩ e 2 ∙ ≠ ∅ , 如图 1.17b)所 ] c\left[e_1>c_1\to c_1\cap e_2^\bullet\neq\emptyset,如图\text{ 1.17b)所}\right] c[e1>c1→c1∩e2∙=∅,如图 1.17b)所]
示。这种情况称为冲撞(contact)。

定义 1.17
在基本网系统 ( B , E ; F , c 0 ) (B,E;F,c_0) (B,E;F,c0)中, c c c是 Σ \Sigma Σ的一个情态。若存在 b ∈ B b\in B b∈B和 e ∈ E e\in E e∈E,使得
∙ e ⊆ c 且 b ∈ e ∙ ∩ c ^\bullet e\subseteq c\text{ 且 }b\in e^\bullet\cap c ∙e⊆c 且 b∈e∙∩c
则称该系统在情态 c c c下条件 b b b处有冲撞。
多个事件都可以导致一个条件满足,但是其中一个事件发生后后置条件被填满所以不能发生了(因为基本网系统中库所容量上限为1),即为冲撞。
冲突是一个条件能发生多个事件,但是只能发生一个。
冲撞是多个事件能满足一个条件,但是只能发生一个事件后其他不能发生了。
在任何情态下,任一个条件都不存在冲撞的基本网系统称为无冲撞系统(contact-free system)。
冲突关系也可以这样给出定义:在 EN 系统 ( B , E ; F , c ) (B,E;F,c) (B,E;F,c)中,若 e 1 , e 2 ∈ E e_1,e_2\in E e1,e2∈E满足
c [ e 1 > 且 c [ e 2 > 但 ¬ c [ e 1 , e 2 } > c\left[\begin{matrix}{e_{1}>}&{\text{且}c}\\\end{matrix}\right[\begin{matrix}{e_{2}>}&{\text{但}\neg c\left[\begin{matrix}{e_{1},e_{2}}\\\end{matrix}\right\}>}\\\end{matrix} c[e1>且c[e2>但¬c[e1,e2}>
则称 e 1 e_1 e1和 e 2 e_2 e2在 c c c处于冲突。
冲突关系描述了系统的非确定性:在某情况下有两个(或多个)事件都有权发生,但在实际运行过程中,只有一个能真正发生。系统存在冲突之处,正是外界环境可以对其施加控制(加以选择)。
有时候,一个网系统,在某个情态下同时存在并发和冲突,但由于并发事件中的某些事件的发生,会使冲突自动消失。另外还有一种情况,系统在某个情态下存在并发, 而并发事件中不同的事件发生,使得系统可能出现冲突,也可能不出现冲突。上面两种现象称为混惑(confusion)。
混惑:
在某个情态下同时存在并发和冲突,但由于并发事件中的某些事件的发生,会使冲突自动消失。
系统在某个情态下存在并发, 而并发事件中不同的事件发生,使得系统可能出现冲突,也可能不出现冲突。
冲突的出现无法确定!尽量避免ta!
第一种混惑的例子如图 1.18 所示。在这个系统中,既有 e 1 e_1 e1和 e 2 e_2 e2的冲突以及 e 2 e_2 e2和 e 3 e_{3} e3的冲突,又有 e 1 e_1 e1和 e 3 e_3 e3的并发。在 e 1 e_1 e1和 e 2 e_2 e2冲突中,如果选择 e 1 e_1 e1发生,则 e 2 e_2 e2和 e 3 e_3 e3的冲突也就自动消失。

第二种混惑的例子如图 1.19 所示。在该系统中,在当前状态下事件 e 1 e_{1} e1和 e 2 e_{2} e2处于并发。如果事件 e 2 e_2 e2先于 e 1 e_1 e1发生,那么就会产生 e 1 e_1 e1和 e 3 e_3 e3的冲突。反之,若 e 1 e_1 e1先于 e 2 e_2 e2发生,这种冲突就不会出现。
存在混惑的网系统不是好的系统模型,因为在这种网系统的运行中,冲突是否出现无法确定,不便于对系统施加外部控制。在建立实际系统的 Petri 网模型时,应尽量避免出现混惑。
1.5.3 一般Petri网系统中的并发与冲突
之前的讨论在基本网系统,现在引入到一般Petri网当中
从基本网系统引入的并发与冲突等概念,在一般 Petri 网中也存在,而且含义基本相同。但由于不同的网系统的变迁发生规则有所不同,因此有些概念在不同的网系统中表现也略有区别。下面先给出在一般 Petri 网中的并发和冲突的定义。
定义 1.18
设 Σ \Sigma Σ 为一个网系统, t 1 t_1 t1 和 t 2 t_2 t2 是 Σ \Sigma Σ 中的两个变迁。如果 Σ \Sigma Σ 的一个标识 M M M 使得 M [ t 1 ⟩ M[t_1\rangle M[t1⟩ 且 M [ t 2 ⟩ M[t_2\rangle M[t2⟩,那么:
- 若 M [ t 1 ⟩ M 1 → M 1 [ t 2 ⟩ M 2 M[t_1\rangle M_1 \rightarrow M_1[t_2\rangle M_2 M[t1⟩M1→M1[t2⟩M2 且 M [ t 2 ⟩ M 1 → M 2 [ t 1 ⟩ M[t_2\rangle M_1 \rightarrow M_2[t_1\rangle M[t2⟩M1→M2[t1⟩,则称 t 1 t_1 t1 和 t 2 t_2 t2 在 M M M 并发,记为 M { t 1 , t 2 ⟩ M\{t_1, t_2\rangle M{t1,t2⟩。
- 若 M [ t 1 ⟩ M 1 → ¬ M 1 [ t 2 ⟩ M[t_1\rangle M_1 \rightarrow \neg M_1[t_2\rangle M[t1⟩M1→¬M1[t2⟩ 且 M [ t 2 ⟩ M 2 → ¬ M 2 [ t 1 ⟩ M[t_2\rangle M_2 \rightarrow \neg M_2[t_1\rangle M[t2⟩M2→¬M2[t1⟩,则称 t 1 t_1 t1 和 t 2 t_2 t2 在 M M M 冲突(或说在 M M M 处于有效冲突)。
t 1 t_1 t1发生后的新标识 M 1 M_1 M1可以发生 t 2 t_2 t2,对偶亦然。
t 1 t_1 t1发生后的新标识 M 1 M_1 M1可以不发生 t 2 t_2 t2,对偶亦然。
就是把情态 c c c换成了标识 M M M。
从定义上看,一般网系统的并发和冲突概念同基本网系统中的定义是一致的,但在实际表现上,却有一些区别。
一般网系统中无冲撞概念
首先,一般 Petri 网中没有冲撞的概念。这是因为 Petri 网中的库所容量为无限大, 因此,在 Petri 网中,只要一个变迁的前集各库所有足够的标志,该变迁就可以发生。即使该变迁的后集中某些库所含有标志,也不影响变迁的发生。
阻塞(有容量函数K的P/T系统,类似于冲撞)
对于有容量函数 K K K的 P/T 系统,由于对库所容量有一定的容量限制,有时也会出现类似于冲撞的情况,但情况又不完全相同。考察图 1.20 的 P/T 系统,为便于观察,我们把各库所的容量函数值标在表示该库所的小圆圈旁。在这个PT 系统中,变迁 t 1 t_1 t1的前集只有一个元素 s 1 s_1 s1。在当前标识下, s 1 s_1 s1中含有 3 个标志,等于弧 ( s 1 , t 1 ) (s_1,t_1) (s1,t1)上的权。但由于 t 1 t_1 t1的后集库所 s 2 s_2 s2中已有 3 个标记,如果 t 1 t_{1} t1发生将向 s 2 s_{2} s2送入 2 个标记,标记总数(5) 将超过 s 2 s_2 s2的容量( K ( s 2 ) = 4 K(s_2)=4 K(s2)=4),因此在当前标识下, t 1 t_1 t1不能发生。然而,如果在当前状态下, t 2 t_2 t2先发生, t 2 t_2 t2发生后, s 2 s_2 s2中只剩余一个标志。这时,虽然作为 t 1 t_1 t1的后集库所 s 2 s_2 s2中非空,但其容量足以容纳 t 1 t_1 t1发生后送到 s 2 s_2 s2的标志,所以在这种情况下 t 1 t_1 t1就可能发生。这种情况反映了实际系统中的阻塞现象。因此,有人直接把这种情况称之为阻塞。

在 Petri 网中, ∙ t 1 ∩ ∙ t 2 ≠ ∅ ^\bullet t_1\cap^\bullet t_2\neq\emptyset ∙t1∩∙t2=∅是变迁 t 1 t_1 t1和 t 2 t_2 t2可能发生冲突的一个必要条件,但不是充分条件。考察图 1.21 的 Petri 网系统。在该网系统中,“ t 1 ∩ ∙ t 2 = { s 2 } ≠ ∅ t_1\cap^{\bullet}t_2=\{s_2\}\neq\emptyset t1∩∙t2={s2}=∅,然而在当前标识下, t 1 t_1 t1和 t 2 t_2 t2非但不处于有效冲突,而且地地道道处于并发。

总之,对各种网系统中的并发和冲突的分析,其根本依据是定义 1.18 和各类网系统的变迁发生规则,切不可只看到一点局部结构就轻易下结论。
一般Petri网中并发与冲突共存情况
在一般 Petri 网中,也存在并发与冲突共存的情况,除了图 1.17 和图 1.18 那样的混惑的情况外,图 1.22a)的网系统是一个有趣的例子。

在当前标识下,变迁 t 1 t_1 t1和 t 2 t_2 t2处于并发。但如果 t 1 t_1 t1或 t 2 t_2 t2有一个先发生,在新的标识下 t 1 t_1 t1和 t 2 t_2 t2便处于有效冲突。不过,对于这种情况,可以施加外部控制。图 1.22b) 便是对其施加控制后的一个例子。在这里,我们在网系统中加入库所 s 4 s_{4} s4和 s 5 s_5 s5使 s 4 t 1 s 5 t 2 s_4t_1s_5t_2 s4t1s5t2形成一个控制回路。加上这样的控制装置后, t 1 t_1 t1和 t 2 t_2 t2的有效冲突已经消失。这个控制装置起到了使变迁 t 1 t_1 t1和 t 2 t_2 t2轮流分享它们的公共资源(库所 s 1 s_{1} s1的标志)的作用。
加了一个控制回流,让他们轮流发生,共同分享 s 1 s_1 s1
相关文章:

【Petri网导论学习笔记】Petri网导论入门学习(七) —— 1.5 并发与冲突
导航 1.5 并发与冲突1.5.1 并发定义 1.14定义 1.15 1.5.2 冲突定义 1.17 1.5.3 一般Petri网系统中的并发与冲突定义 1.18一般网系统中无冲撞概念阻塞(有容量函数K的P/T系统,类似于冲撞)一般Petri网中并发与冲突共存情况 1.5 并发与冲突 Petr…...

MongoDB常用语句
1.只统计记录总数: let result await CorrectionRecordModel.countDocuments(db);2.数组遍历,循环体中可以有调用异步函数: for(let item of result2){if(item && Tool.checkNotEmptString(item.auth_id) && (item.status …...

自动创作PPT 利用提示词和大模型自动创建ppt
背景 ppt创作可以分为3个步骤:1.大纲撰写;2.内容填充;3.ppt实现。我前几天用十分钟的时间做了一个ppt,主讲大模型测评。这里给大家分享一下我的创作过程。 关于步骤1和步骤2,最近发现一个非常好的提示词,…...

二分类评价指标AUROC和AUPR
文章目录 一、AUROC(Area Under the Receiver Operating Characteristic Curve)二、AUPR(Area Under the Precision-Recall Curve)三、区别3.1 案例3.2 如何选择? 在分类任务中, AUROC(受试者工…...

雅迪控股营收、净利润和毛利下滑:销量大幅减少,屡屡抽查不合格
《港湾商业观察》廖紫雯 日前,雅迪集团控股有限公司(以下简称:雅迪控股,01585.HK)发布业绩报告,披露2024年上半年营收净利双下滑等情况,在业绩承压的情况下,雅迪控股遭多家券商下调…...

【网络安全】记一次漏洞挖掘
Spring Cloud Data Flow 热点漏洞详细分析 环境搭建 2.10.0 - 2.11.2版本都可以,这里下的2.11.2 源码下载https://github.com/spring-cloud/spring-cloud-dataflow/tree/v2.11.2 在src/docker-compose里面是有docker文件的,使用docker即可 最近是爆出…...
Redis遇到Hash冲突怎么办?
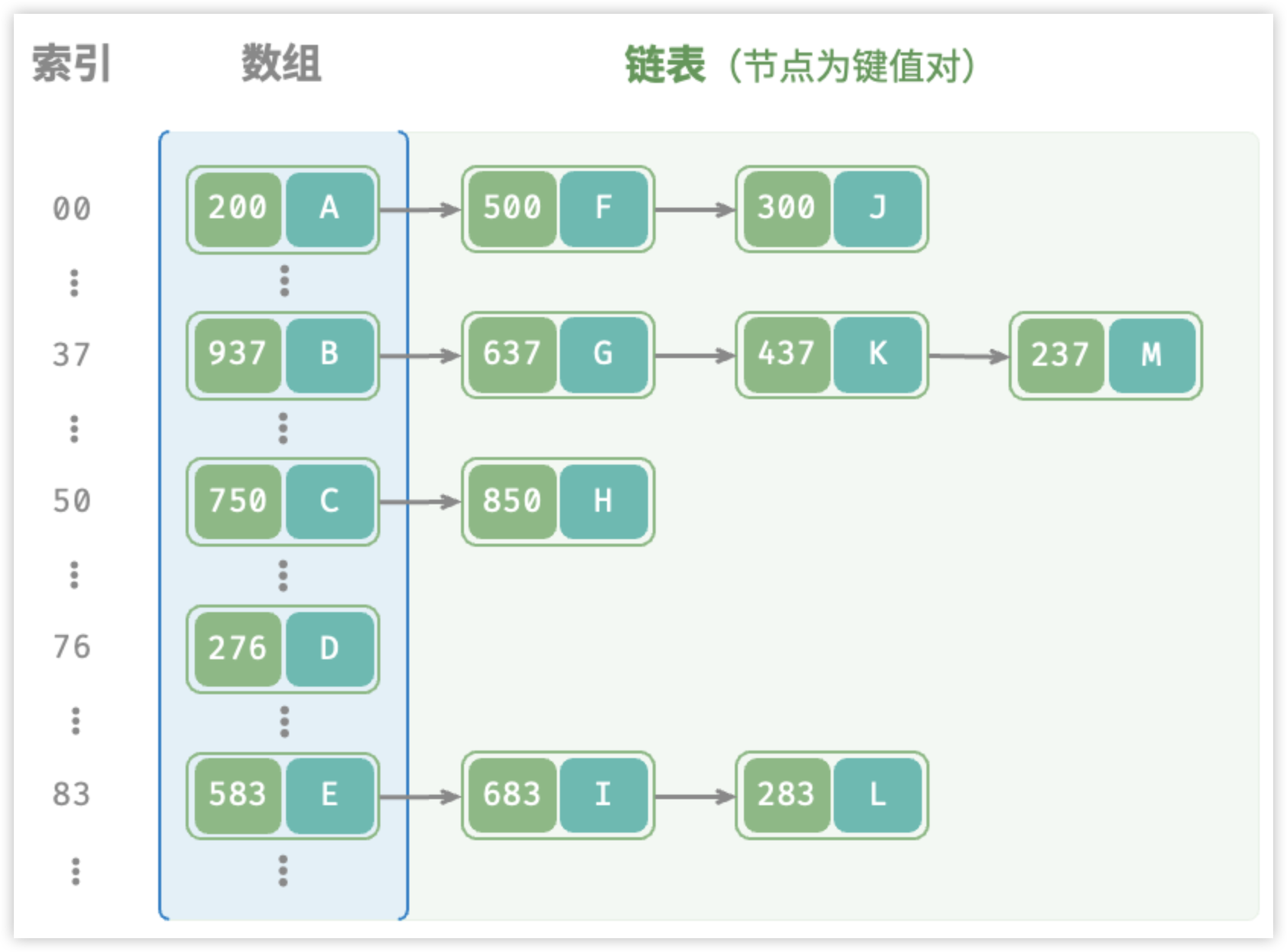
这是小伙伴之前遇到的一个面试题,感觉也是一个经典八股,和大伙分享下。 一 什么是 Hash 冲突 Hash 冲突,也称为 Hash 碰撞,是指不同的关键字通过 Hash 函数计算得到了相同的 Hash 地址。 Hash 冲突在 Hash 表中是不可避免的&am…...

React综合指南(四)
61、描述React事件处理。 为了解决跨浏览器兼容性问题,React中的事件处理程序将传递SyntheticEvent实例,该实例是React跨浏览器本机事件的跨浏览器包装器。这些综合事件具有与您惯用的本机事件相同的界面,除了它们在所有浏览器中的工作方式相…...

Spring集成Redisson及存取几种基本类型数据
目录 一.什么是Redisson 二.为什么要使用Redisson 三.Spring集成Redisson 1.添加依赖 2.添加配置信息 3.添加redisson配置类 四.Redisson存取各种类型数据 1.字符串(String类型) 存储 获取 2.object对象类型 1.实体类信息 2.存储 3.获取 3.List集合类型 第一种…...

Maplibre-gl\Mapbox-gl改造支持对矢量瓦片加密
Maplibre-gl是Mapbox-gl剔除自带地图服务之后的一个分支,代码很相似。Maplibre-gl\Mapbox-gl使用的pbf格式的矢量瓦片,数据量小,渲染效果好。但也存在着信息泄露的风险。但如果想使用这个开发框架的前端渲染效果,还必须要使用这个格式。最近研究了一下如何对矢量瓦片进行加…...
【功能安全】技术安全概念TSC
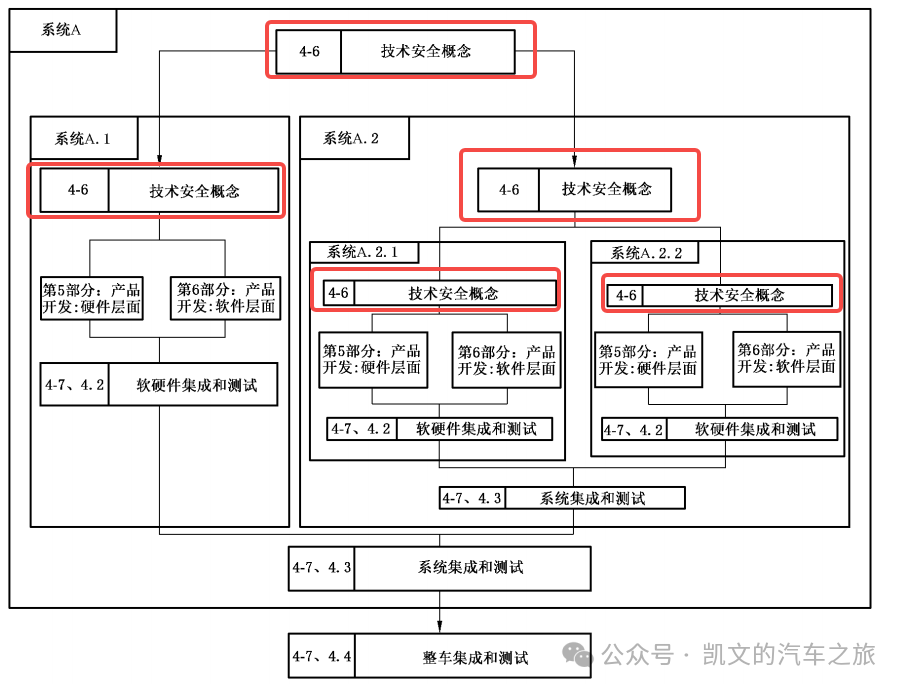
目录 01 TSC定义 02 TSC注意事项 03 TSC案例 📖 推荐阅读 01 TSC定义 所处位置 TSC:Technical safety concept技术安全概念 TSR:Technical safety requirement技术安全需求 在系统开发阶段属于安全活动4-6 系统层产品开发示例 TSC目的...

Spark数据源的读取与写入、自定义函数
1. 数据源的读取与写入 1.1 数据读取 读文件 read.jsonread.csv csv文件由两个部分组成:头部数据(也就是字段数据)、行数据。 read.orc 读数据库 read.jdbc(jdbc连接地址,table‘表名’,properties{‘user’用户名,‘password’密码,‘driv…...

LeetCode 每日一题 2024/10/14-2024/10/20
记录了初步解题思路 以及本地实现代码;并不一定为最优 也希望大家能一起探讨 一起进步 目录 10/14 887. 鸡蛋掉落10/15 3200. 三角形的最大高度10/16 3194. 最小元素和最大元素的最小平均值10/17 3193. 统计逆序对的数目10/18 3191. 使二进制数组全部等于 1 的最少操…...

接口测试(六)jmeter——参数化(配置元件 --> 用户定义的变量)
一、jmeter——参数化(配置元件 --> 用户定义的变量) 注:示例仅供参考 1. 参数化格式:${变量名} 2. 配置元件:用户定义的变量 3. 添加【用户定义的变量】,【线程组】–>【添加】–>【配置元件】–…...

【学习笔记】网络流
背景 马上ICPC了,很惊奇的发现自己没整理网络流的板子。 最大流 dinic 这里选用的是二分图最大匹配的板子:飞行员配对方案问题 #include<bits/stdc.h> #define int long long using namespace std; const int N1e67,inf1e18; struct E {int to…...
【鸡翅Club】项目启动
一、项目背景 这是一个 C端的社区项目,有博客、交流,面试学习,练题等模块。 项目的背景主要是我们想要通过面试题的分类,难度,打标,来评估员工的技术能力。同时在我们公司招聘季的时候,极大的…...

python+大数据+基于热门视频的数据分析研究【内含源码+文档+部署教程】
博主介绍:✌全网粉丝10W,前互联网大厂软件研发、集结硕博英豪成立工作室。专注于计算机相关专业毕业设计项目实战6年之久,选择我们就是选择放心、选择安心毕业✌ 🍅由于篇幅限制,想要获取完整文章或者源码,或者代做&am…...

【电子电力】基于PMU相量测量单元的电力系统状态评估
摘要 相量测量单元(PMU)作为一种精确且快速的实时监控设备,在电力系统状态评估中发挥了重要作用。本文研究了在没有PMU和部署PMU情况下,电力系统的电压角度和电压幅值估计误差的差异。通过比较实验结果,发现PMU的应用…...
)
ubuntu修改默认开机模式(图形/终端)
将 Ubuntu 16 系统设置为开机进入终端模式: 打开终端。编辑 Grub 配置文件:sudo nano /etc/default/grub。找到 GRUB_CMDLINE_LINUX_DEFAULT 行,将其修改为 GRUB_CMDLINE_LINUX_DEFAULT"text"。保存并退出编辑器(Ctrl …...

LaMI-DETR:基于GPT丰富优化的开放词汇目标检测 | ECCV‘24
现有的方法通过利用视觉-语言模型(VLMs)(如CLIP)强大的开放词汇识别能力来增强开放词汇目标检测,然而出现了两个主要挑战:(1)概念表示不足,CLIP文本空间中的类别名称缺乏…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...
