【日志】力扣刷题 -- 轮转数组
2024.10.06
【力扣刷题】
经典面试150—转轮数组—中等
189. 轮转数组 - 力扣(LeetCode)
第一次做,暴力循环
// 超出时间限制
void rotate(int* nums, int numsSize, int k) {for(int i = 0; i < k; i++){int right = numsSize - 1;int temp = nums[numsSize - 1];for(int j = numsSize - 2; j >= 0; j--){nums[j + 1] = nums[j];}nums[0] = temp;}
}官方答案一:
使用额外数组
创建新的数组就可以拿到原数组的数据,又可以对新数组进行排序。
用 % numsSize 就会得到一个从 k 开始的数组索引,
就是说 newArray[ k ] = nums[0]
当 (i + k) 等于 numsSize 时,结果为0,newArray的下标索引为零
也就是 newArray[ 0 ] = nums[i];
此时,要移动到前面的数就开始从 0 赋值到 k-1
void rotate(int* nums, int numsSize, int k) {int newArray[numsSize];for(int i = 0; i < numsSize; i++){newArray[(i + k) % numsSize] = nums[i];}for(int i = 0; i < numsSize; i++){nums[i] = newArray[i];}
}【数据结构】
暂无
//相关代码【Unity】
UI框架搭建学习,暂无更多
【奇思妙想】
《末日狂花钱》
光看名字与《末路狂花钱》很像,实际灵感来源于《瑞克与莫迪》(忘记第几季第几集),爷孙二人来到一个即将因太阳爆炸而毁灭的星球上狂欢,这里正举办一个末日派对,一直到毁灭为止。我想让贯穿整个游戏的核心四象是:The End Day is coming 尽情狂欢吧。
游戏类型的话可以是自由探索世界,也可以是剧情体验。
如果说GTA5是自由的,那这个就是释放天性,放纵的。标签的话恐怕得打上涉及学新,保利以及瑟琴。
剧情:大概上是一开始所有人都取出钱来花,印钞厂开始疯狂印钱,商品到最后都是免费的?想和爱的人共度最后的时光?想做以前根本不敢做的事情(反抗?强迫?紫砂?还是彻底疯狂)?秩序、混乱、提前消亡(新三体)?
这让我想起了《猪猪侠之囧囧危机》。
——每天努力十五分钟,一年就努力了5475分钟,也就是91.25小时。(记得乘上0.7,这是扣去双休和法定的节假日的时间的)
相关文章:

【日志】力扣刷题 -- 轮转数组
2024.10.06 【力扣刷题】 经典面试150—转轮数组—中等 189. 轮转数组 - 力扣(LeetCode) 第一次做,暴力循环 // 超出时间限制 void rotate(int* nums, int numsSize, int k) {for(int i 0; i < k; i){int right numsSize - 1;int temp…...

Java 项目 Dockerfile 示例:从基础镜像选择到环境变量配置的详细指南
Java 项目 Dockerfile 示例:从基础镜像选择到环境变量配置的详细指南 本文提供了一个 Java 项目的 Dockerfile 示例,展示了如何为 Java 应用创建高效的 Docker 镜像。Dockerfile 从 OpenJDK 8 的 Java 运行环境开始,配置了工作目录和 JVM 启…...

WebGL编程指南 - 高级变换与动画基础
学习使用一个矩阵变换库,该库封装了矩阵运算的数学细节。快速上手使用该矩阵库,对图形进行复合变换。在该矩阵库的帮助下,实现简单的动画效果。 矩阵变换库:cuon-matrix.js OpenGL中的函数: 书中 cuon-matrix.js 函数…...

银行客户贷款行为数据挖掘与分析
#1024程序员节 | 征文# 在新时代下,消费者的需求结构、内容与方式发生巨大改变,企业要想获取更多竞争优势,需要借助大数据技术持续创新。本文分析了传统商业银行面临的挑战,并基于knn、逻辑回归、人工神经网络三种算法࿰…...

制程质量管理方案设计
质量管理系统框架——QMS 涵盖产生产制造体系的全生命周期的质量管理过程 与SAP、WMS、MES、OA等业务系统进行集成,整合各业务系统中的质量信息 利用整合的全价值链质量信息,寻找质量改进点和质量创新点 系统功能模块管理 系统管理:用户管理…...

uniapp移动端优惠券! 附源码!!!!
本文为常见的移动端uniapp优惠券,共有6种优惠券样式(参考了常见的优惠券),文本内容仅为示例,您可在此基础上调整为你想要的文本 预览效果 通过模拟数据,实现点击使用优惠券让其变为灰色的效果(模…...

【分布式技术】中间件-zookeeper安装配置
文章目录 安装部署1. 安装ZooKeeper2. 配置ZooKeeper3. 启动ZooKeeper服务器4. 使用ZooKeeper命令行客户端5. 使用ZooKeeper的四个基本操作6. ZooKeeper集群模式7. 安全和权限8. 监控和日志 相关文献 安装部署 在Linux环境中操作ZooKeeper通常涉及以下几个方面: 1…...

高等数学 7.6高阶线性微分方程
文章目录 一、线性微分方程的解的结构*二、常数变易法 方程 d 2 y d x 2 P ( x ) d y d x Q ( x ) f ( x ) (1) \cfrac{\mathrm{d}^2 y}{\mathrm{d}x^2} P(x) \cfrac{\mathrm{d}y}{\mathrm{d}x} Q(x) f(x) \tag{1} dx2d2yP(x)dxdyQ(x)f(x)(1) 叫做二阶线性微分方程。…...

LSP的建立
MPLS需要为报文事先分配好标签,建立一条LSP,才能进行报文转发。LSP分为静态LSP和动态LSP两种。 静态LSP的建立 静态LSP是用户通过手工为各个转发等价类分配标签而建立的。由于静态LSP各节点上不能相互感知到整个LSP的情况,因此静态LSP是一个…...

huggingface的数据集下载(linux下clone)
1. 安装lfs sudo apt-get install git-lfs 或者 apt-get install git-lfs 2. git lfs install git lfs install 3. git clone dataset包 第2,3步骤的截图如下:...

Java使用dom4j生成kml(xml)文件遇到No such namespace prefix: xxx is in scope on:问题解决
介绍addAttribute和addNamepsace: addAttribute 方法 addAttribute 方法用于给XML元素添加属性。属性(Attributes)是元素的修饰符,提供了关于元素的额外信息,并且位于元素的开始标签中。属性通常用于指定元素的行为或样式&#…...

深入探讨Java中的LongAdder:使用技巧与避坑指南
文章目录 一、什么是LongAdder?二、LongAdder的简单使用示例代码: 三、LongAdder的工作原理四、LongAdder的常见使用场景五、使用LongAdder时的注意事项(避坑指南)1. 不要滥用LongAdder2. sum()方法与精度问题3. 避免过度使用rese…...

【本科毕业设计】基于单片机的智能家居防火防盗报警系统
基于单片机的智能家居防火防盗报警系统 相关资料链接下载摘要Abstract第1章 绪论1.1课题的背景1.2 研究的目的和意义 第2章 系统总体方案设计2.1 设计要求2.2 方案选择和论证2.2.1 单片机的选择2.2.2 显示方案的选择 第3章 系统硬件设计3.1 整体方案设计3.1.1 系统概述3.1.2 系…...

C语言 动态数据结构的C语言实现单向链表-2
建立一个单向链表 在单向链表中查找节点---查找尾节点 在单向链表中查找节点 --- 查找第 n 个节点 向单向链表中插入一个节点 向单向链表的尾部插入一个节点 向单向链表中某节点后插入一个节点 向单向链表中插入一个节点 删除单向链表中的某一节点 链表 vs 数组 动态数据结构...

Github 2024-10-23C开源项目日报 Top10
根据Github Trendings的统计,今日(2024-10-23统计)共有10个项目上榜。根据开发语言中项目的数量,汇总情况如下: 开发语言项目数量C项目10PLpgSQL项目1Redis - 内存数据库和数据结构服务器 创建周期:5411 天开发语言:C协议类型:BSD 3-Clause “New” or “Revised” Licen…...
: relocation报错解决)
ubuntu20.04 opencv4.0 /usr/local/lib/libgflags.a(gflags.cc.o): relocation报错解决
在一个只有ubuntu20.04的docker环境中配置opencv4.0.0, 什么库都没有,都要重新安装, 其他的问题在网上都找到了解决方案,唯独这个问题比较棘手: [ 86%] Linking CXX executable …/…/bin/opencv_annotation /usr/bin/ld: /usr/lo…...
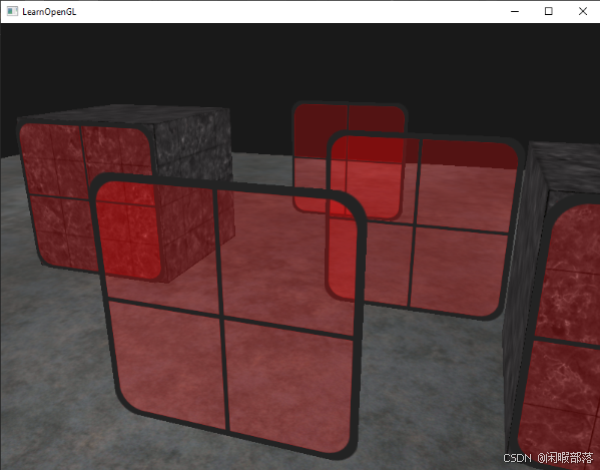
android openGL ES详解——混合
一、混合概念 混合是一种常用的技巧,通常可以用来实现半透明。但其实它也是十分灵活的,你可以通过不同的设置得到不同的混合结果,产生一些有趣或者奇怪的图象。混合是什么呢?混合就是把两种颜色混在一起。具体一点,就…...

计网--物理层
目录 物理层的任务 1、常见概念 2、信道极限容量 3、传输介质 (1)导引型传输介质 (2)非导引型传输介质 4、信道复用技术 (1)频分 / 时分 复用 (2)波分复用WDM (…...

算法的学习笔记—数组中的逆序对(牛客JZ51)
😀前言 在算法和数据结构领域,"逆序对"是一个经典问题。它在数组中两个数字之间定义,若前面的数字大于后面的数字,则这两个数字组成一个逆序对。我们要做的就是,给定一个数组,找出数组中所有的逆…...

Golang | Leetcode Golang题解之第498题对角线遍历
题目: 题解: func findDiagonalOrder(mat [][]int) []int {m, n : len(mat), len(mat[0])ans : make([]int, 0, m*n)for i : 0; i < mn-1; i {if i%2 1 {x : max(i-n1, 0)y : min(i, n-1)for x < m && y > 0 {ans append(ans, mat[x…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

spring Security对RBAC及其ABAC的支持使用
RBAC (基于角色的访问控制) RBAC (Role-Based Access Control) 是 Spring Security 中最常用的权限模型,它将权限分配给角色,再将角色分配给用户。 RBAC 核心实现 1. 数据库设计 users roles permissions ------- ------…...

C++_哈希表
本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说,直接开始吧! 一、基础概念 1. 哈希核心思想: 哈希函数的作用:通过此函数建立一个Key与存储位置之间的映射关系。理想目标:实现…...
