第8次CCF CSP认证真题解
1、最大波动
题目链接:https://sim.csp.thusaac.com/contest/8/problem/0
100分代码:
#include <iostream>
#include <algorithm>
using namespace std;
int main(int argc, char *argv[])
{int n;cin >> n;int a[1010];for(int i = 0; i < n; i++){cin >> a[i];}int max_value = 0;for(int i = 1; i < n; i++){max_value = max(max_value , abs(a[i] - a[i-1]));}cout << max_value << endl;return 0;
}评测结果:

2、火车购票
题目链接:https://sim.csp.thusaac.com/contest/8/problem/1
本题需要注意一个边界条件:20排座位中每排都有被安排了,且剩下的人购买的车票无法安排在同一排,只能安排在编号最小的几个空座位中。如果边界条件考虑少了,可能就只有90分。
未考虑边界条件的90分代码:
#include <iostream>
using namespace std;
int main(int argc, char *argv[])
{int n;cin >> n;int p[110];for(int i = 1; i <= n; i++){cin >> p[i]; }int a[30][15] = {0};for(int i = 1; i <= n; i++){int count2 = 0;for(int j = 1; j <= 20; j++){int count1 = 0; for(int k = 1; k <= 5; k++){if(a[j][k] == 0)count1++;}if(count1 >= p[i]){int count3 = 0;for(int t = 1; t <= 5; t++){if(a[j][t] == 0){a[j][t] = (j-1)*5+t;cout << a[j][t] << " "; count3++;}if(count3 == p[i])break; }cout << endl;break;}else if(count1 < p[i]){count2++;continue;}}}return 0;
}评测结果:

100分代码:
#include <iostream>
using namespace std;
int main(int argc, char *argv[])
{int n;cin >> n;int p[110];for(int i = 1; i <= n; i++){cin >> p[i]; }int a[30][15] = {0};for(int i = 1; i <= n; i++){int count2 = 0;for(int j = 1; j <= 20; j++){int count1 = 0; for(int k = 1; k <= 5; k++){if(a[j][k] == 0)count1++;}if(count1 >= p[i]){int count3 = 0;for(int t = 1; t <= 5; t++){if(a[j][t] == 0){a[j][t] = (j-1)*5+t;cout << a[j][t] << " "; count3++;}if(count3 == p[i])break; }cout << endl;break;}else if(count1 < p[i]){count2++;continue;}}if(count2 == 20){ //边界条件 for(int x = 1; x <= 20; x++){for(int y = 1; y <= 5; y++){if(a[x][y] == 0){a[x][y] = (x-1)*5+y;cout << a[x][y] << " ";}} }}}return 0;
}评测结果:

相关文章:

第8次CCF CSP认证真题解
1、最大波动 题目链接:https://sim.csp.thusaac.com/contest/8/problem/0 100分代码: #include <iostream> #include <algorithm> using namespace std; int main(int argc, char *argv[]) {int n;cin >> n;int a[1010];for(int i …...
)
2024昆明ICPC A. Two-star Contest(直观命名+详细注释)
Problem - A - Codeforces 思路: 按照等级排序,维护同等级最大评分,每个等级的总评分至少比其第前一个等级的最大评分大1分 吐槽: 思路不难,但坑好多,感觉全踩了一遍 坑:(按解决…...

【算法刷题指南】双指针
🌈个人主页: 南桥几晴秋 🌈C专栏: 南桥谈C 🌈C语言专栏: C语言学习系列 🌈Linux学习专栏: 南桥谈Linux 🌈数据结构学习专栏: 数据结构杂谈 🌈数据…...
HTML,CSS,JavaScript三件套
前言 1.HTML 就是用来写网页的 就是超文本标记语言 1.1快速入门 标签是根标签,就是开始的地方 head就是头,加载一些资源信息,和展示title标题的地方,比如html快速入门那几个字就是title标题标签 body是身体,就是正…...
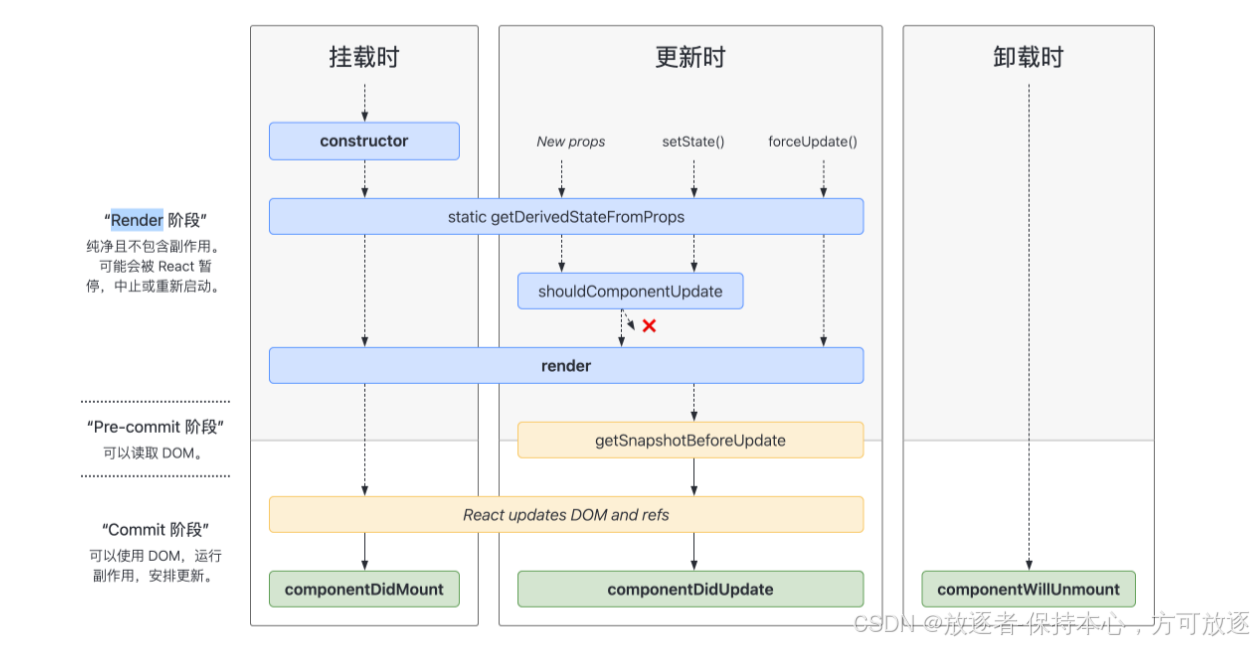
react 总结+复习+应用加深
文章目录 一、React生命周期1. 挂载阶段(Mounting)补充2. 更新阶段(Updating)补充 static getDerivedStateFromProps 更新阶段应用补充 getSnapshotBeforeUpdate3. 卸载阶段(Unmounting) 二、React组件间的…...

关于 API
关于 API $set 问法:有没有遇到过数据更新了但视图没有更新的情况? <template><div>{{arr}}<button click"btn"></button></div> </template><script> export default {name:"Home"da…...

第15次CCF CSP真题解
1、小明上学 题目链接:https://sim.csp.thusaac.com/contest/15/problem/0 本题是模拟红绿灯计时的题,根据红绿灯转换规则可知,红灯后面通常是绿灯,绿灯后面是黄灯,黄灯过后又是红灯。根据题意,当k 0时&…...
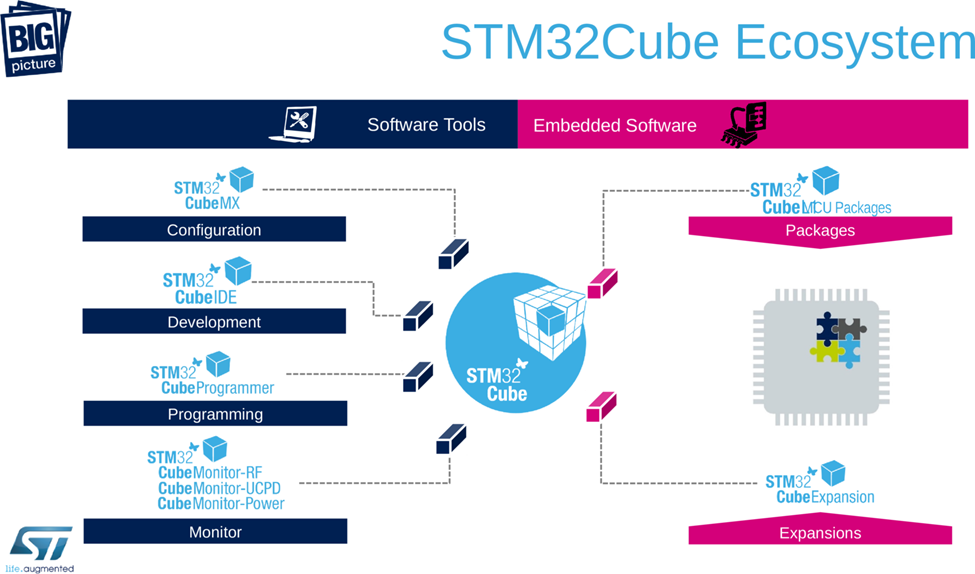
STM32硬件平台
STM32 系列是 STMicroelectronics 设计的高度灵活、广泛应用的微控制器(MCU)系列,支持从低功耗应用到高性能处理的需求,适用于工业、汽车、消费电子和物联网等广泛领域。STM32 系列具有广泛的硬件种类和丰富的功能,以下…...

一文讲明白大模型分布式逻辑(从GPU通信原语到Megatron、Deepspeed)
1. 背景介绍 如果你拿到了两台8卡A100的机器(做梦),你的导师让你学习部署并且训练不同尺寸的大模型,并且写一个说明文档。你意识到,你最需要学习的就是关于分布式训练的知识,因为你可是第一次接触这么多卡…...

【人工智能-初级】第6章 决策树和随机森林:浅显易懂的介绍及Python实践
文章目录 一、决策树简介二、决策树的构建原理2.1 决策树的优缺点优点缺点 三、随机森林简介3.1 随机森林的构建过程3.2 随机森林的优缺点优点缺点 四、Python实现决策树和随机森林4.1 导入必要的库4.2 加载数据集并进行预处理4.3 创建决策树模型并进行训练4.4 可视化决策树4.5…...
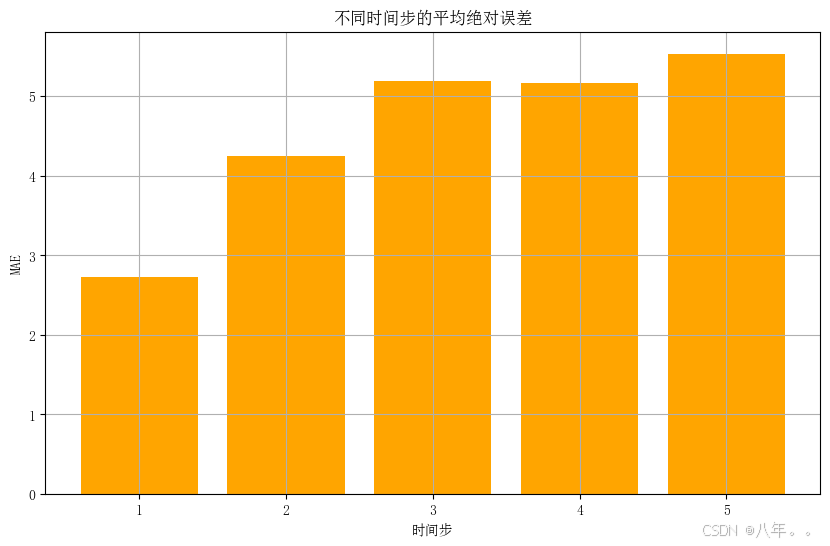
时间序列预测(九)——门控循环单元网络(GRU)
目录 一、GRU结构 二、GRU核心思想 1、更新门(Update Gate):决定了当前时刻隐藏状态中旧状态和新候选状态的混合比例。 2、重置门(Reset Gate):用于控制前一时刻隐藏状态对当前候选隐藏状态的影响程度。…...

李东生牵手通力股份IPO注册卡关,三年近10亿“清仓式分红”引关注
《港湾商业观察》施子夫 9月27日,通力科技股份有限公司(以下简称,通力股份)再度提交了注册申请,实际上早在去年11月6日公司已经提交过注册,看起来公司注册环节面临卡关。公开信息显示,通力股份…...

Android13、14特殊权限-应用安装权限适配
Android13、14特殊权限-应用安装权限适配 文章目录 Android13、14特殊权限-应用安装权限适配一、前言二、权限适配三、其他1、特殊权限-应用安装权限适配小结2、dumpsys package查看获取到了应用安装权限3、Android权限系统:应用操作管理类AppOpsManager(…...
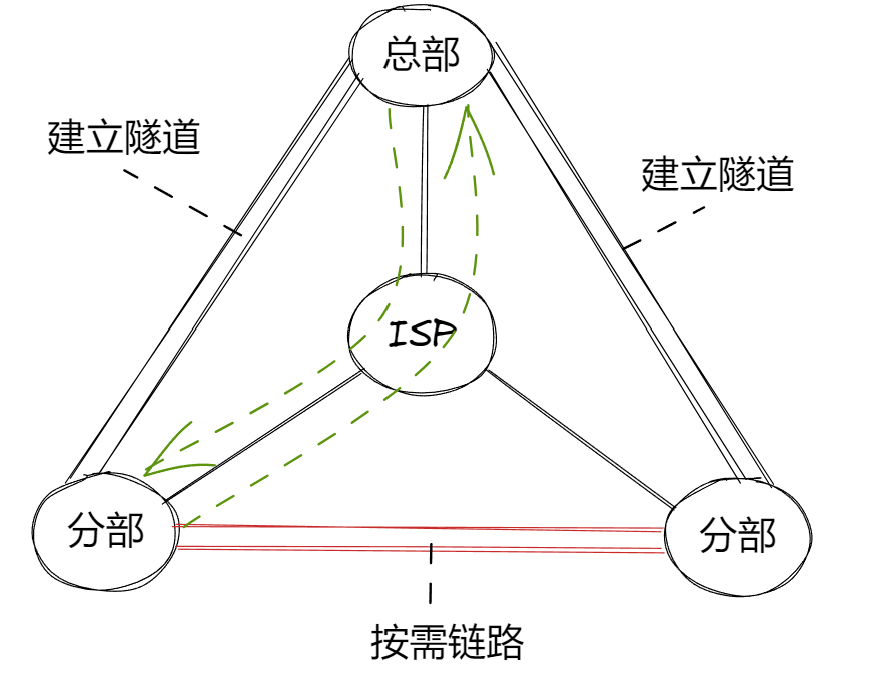
DMVPN协议
DMVPN(Dynamic Multipoint VPN)动态多点VPN 对于分公司和分总公司内网实现通信环境下,分公司是很多的。我们不可能每个分公司和总公司都挨个建立ipsec隧道 ,而且如果是分公司和分公司建立隧道,就会很麻烦。此时我们需…...
-零钱兑换II)
leetcode动态规划(十八)-零钱兑换II
题目 322.零钱兑换II 给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。 计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。 你可以认为每种硬…...

2024 CSP-J 题解
2024 CSP-J题解 扑克牌 题目给出了一整套牌的定义,但是纯粹在扯淡,完全没有必要去判断给出的牌的花色和点数,我们用一个循环来依次读入每一张牌,如果这个牌在之前出现过,我们就让答案减一。这里建议用map、unorde…...

GPU 服务器厂家:中国加速计算服务器市场的前瞻洞察
科技的飞速发展,让 GPU 服务器在加速计算服务器领域的地位愈发凸显。中国加速计算服务器市场正展现出蓬勃的生机,而 GPU 服务器厂家则是这场科技盛宴中的关键角色。 从市场预测的趋势来看,2023 年起,中国加速计算服务器市场便已展…...

Hadoop集群修改yarn队列
1.修改默认的default队列参数 注意: yarn.scheduler.capacity.root.队列名.capacity总和不能超过100 <property><name>yarn.scheduler.capacity.root.queues</name><value>default,hive,spark,flink</value><description>The…...

【GPIO】2.ADC配置错误,还是能得到电压数据
配置ADC功能时,GPIO引脚弄错了,P1写成P2,但还是配置成功,能得到电压数据。 首先一步步排查: 既然引脚弄错了,那引脚改为正确的引脚,能得到数据通过第一步判断,GPIO配置似乎是不起作…...

css-元素居中方式
<section class"wrapper"><div class"content">Content goes here</div> </section>1. 使用 Flexbox Flexbox 是一种现代的布局方法,可以轻松实现居中。 .wrapper {display: flex; /* 使用 Flexbox …...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

数据库正常,但后端收不到数据原因及解决
从代码和日志来看,后端SQL查询确实返回了数据,但最终user对象却为null。这表明查询结果没有正确映射到User对象上。 在前后端分离,并且ai辅助开发的时候,很容易出现前后端变量名不一致情况,还不报错,只是单…...

【版本控制】GitHub Desktop 入门教程与开源协作全流程解析
目录 0 引言1 GitHub Desktop 入门教程1.1 安装与基础配置1.2 核心功能使用指南仓库管理日常开发流程分支管理 2 GitHub 开源协作流程详解2.1 Fork & Pull Request 模型2.2 完整协作流程步骤步骤 1: Fork(创建个人副本)步骤 2: Clone(克隆…...
