【深入浅出】深入浅出transformer(附面试题)
本文的目的是为了帮助大家面试transformer,会结合我的面试经历以及看法去讲解transformer,并非完整的技术细致讲解,介意请移步。
结构
提到transformer网络模型,大家脑海中是否有这张图呢?

这是网络结构中经典的编解码网络结构。
编码器:由𝑁层编码层组成,每层对输入序列进行编码。
解码器:也由𝑁层解码层组成,并结合编码器输出生成最终输出序列。
编码器
位置编码
可以看到,输入到编码其中,首先经过了一个位置编码,这个位置编码是怎么设计的?有什么用?
看公式

- 有什么用?
众所周知,transformer结构依赖于自注意力机制,可以并行的计算整个序列的关系,但是他没有固有的顺序意识,这时候就需要位置编码了。 - 怎么设计的?
位置编码是一组具有固定模式的向量,其计算方式主要是基于正弦和余弦函数。句子长度为n,维度索引为i,总维度为d,通过这种方法确保不同位置的编码值是唯一的,并且在维度上保留平滑的变化。 - 作用?
周期性变化:正弦和余弦的周期性确保了相邻词的编码差异较小,随着位置增大变化逐渐减缓,适应长距离依赖。
平滑的位置信息:正弦和余弦的值随着位置的变化以非线性的方式增加,使模型能够学习词的相对位置信息和词序关系。
距离敏感性:较近的词之间的编码相似度较高,而远距离的词编码差异较大,便于捕捉长短期依赖。
注意力机制(attention)

输入内容经过位置编码后,ctrl +c,v复制成了三份完全一样的,作为QKV。如何理解QKV呢,通俗易懂的讲,Q为搜索关键字,K为搜索相关的分类,V为搜索出的结果,通过QK计算得到权重,然后V得到注意力的结果。
注意力机制的公式是这样的:

是不是向上面讲的QK*V的一个逻辑?那么又聪明的小朋友可能要问了,下面的这个dk是做什么的(高频考点)?
请参考我的这篇文章
【每日一问】transformer中的self-attention中为什么要除以dk?
讲完了注意力机制,那么多头是什么?
多头注意力机制
它将输入的注意力计算拆分为多个“头”,每个头分别计算一组不同的 Q、K、V 向量,并在每个头上并行计算注意力。然后将所有头的输出拼接在一起,再通过线性变换层生成最终的注意力输出。
太官方了?
别急,通俗易懂的讲:
同一份内容,经过不同的处理,能够得到不同的结果。多头注意力中,每个头是一注意力机制,独立的计算词与词之间的相似度,每个头关注不同的细节信息,帮助模型更全面地理解句子中的含义
举例我们有三个头:
- 第一个头可能关注词之间的空间关系,比如“猫”在哪里坐。
- 第二个头可能关注词之间的时间顺序,比如“先有猫再有沙发”。
- 第三个头可能关注词的动作关系,比如“猫是在沙发上‘坐’的”
多头注意力机制就像给模型多副“眼镜”,每副眼镜看到的角度不一样,最终合成的结果让模型能从多方位理解句子。
这样,我们讲完了编码器,接下来讲解解码器
解码器
可以从网络结构图中看出,解码器结构与编码器结构几乎是相同的。但是有两点不同。
-
masked是什么?
masked是transformer中的蒙版。对于解码器来说,不同于以往的时序模型RNN中的解码器,它能够阅读到句子的整个上下文内容,所以在解码器中,需要一些特殊的操作对句子进行处理。
例如在生成句子 “我要吃饭”,生成 “要 时,只能基于 “我” 来生成,而不能提前知道 “吃饭”,如果模型知道了后面的内容,不就相当于透题了吗?这样模型的损失函数无法计算,自然结果会很烂。 -
masked是如何做的?
在解码器的 masked self-attention 中,使用了一个“掩码矩阵”来阻止模型访问未来的信息。

在这个矩阵中,1 表示可以看到对应位置的词,0 表示不能看到。因此,在生成第三个词时,模型只能关注到第一个和第二个词,而不能看到第四个词。
他的效果如下所示:

通过masked机制,强制保证解码器不偷看未来的答案,确保结果每次都是基于已经生成的词语。
底层实现:其实这里masked的底层实现是给不是1的地方给了个很大的负数。还记得attention是怎么计算的吗?是不是有个softmax函数?在softmax函数中,x为很大的负数的时候,经过softmax处理后结果为0。这就是处理方式。 -
编码器对解码器的连线是什么?
其实就是多头注意力中的K和V啦。解码器传递过来的是Q,然后通过这种方式计算注意力机制。

这样来看是不是就好很多了呢?
讲解完啦,接下来看看这些面试题能不能答上来吧!
面试题
- 编码器中距离编码是什么?
- 讲解一下注意力机制。
- 多头注意力是什么?作用是什么?有什么优点?
- 编码器和解码器有什么不同?
- masked是什么机制?如何实现?
- 简单讲一下Transformer中的残差结构以及意义。
- Encoder端和Decoder端是如何进行交互的?
- 你还了解哪些关于位置编码的技术,各自的优缺点是什么?
相关文章:

【深入浅出】深入浅出transformer(附面试题)
本文的目的是为了帮助大家面试transformer,会结合我的面试经历以及看法去讲解transformer,并非完整的技术细致讲解,介意请移步。 结构 提到transformer网络模型,大家脑海中是否有这张图呢? 这是网络结构中经典的编解…...
苹果重大更新,macOS与iOS同时推出更新!功能真好用
前言 这几天,苹果更新了macOS和iOS的系统版本!macOS Sequoia 版本号15.1 iOS版本号18.1 小白更新设备系统的时间已经算比较晚的了,但好在更新得很及时!因为这次更新的功能很合小白的胃口啊!咱们先来看看本次更新了什么…...

刘艳兵-DBA016-在您的数据库中,SALES表存在于SH用户中,并且启用了统一审计。作为DBA,您成功执行了以下指令:
在您的数据库中,SALES表存在于SH用户中,并且启用了统一审计。作为DBA,您成功执行了以下指令: SQL> CREATE AUDIT POLICY sales_pol ACTIONS select on sh.sales; SQL> AUDIT POLICY sales_pol; 关于SALES_POL审计策略,哪个陈…...

力扣题目解析--整数反转
题目 给你一个 32 位的有符号整数 x ,返回将 x 中的数字部分反转后的结果。 如果反转后整数超过 32 位的有符号整数的范围 [−231, 231 − 1] ,就返回 0。 假设环境不允许存储 64 位整数(有符号或无符号)。 示例 1:…...

净水前置需要安装吗?
业主问净水前置需不需要安装?是必须安装吗?这个问题其实很难回答,如果说非要安装,有可能客户会感觉我们在这上面要挣钱, 有很多业主没有安装家里用水也没有问题,如果说不需要安装,现在…...

在深度学习研究方向有哪些创新点
以下是深度学习研究方向的一些创新点: 一、模型架构创新 Transformer架构及其扩展 自注意力机制 Transformer架构摒弃了传统的卷积神经网络(CNN)和循环神经网络(RNN)中的卷积和循环结构,引入了自注意力机…...

YOLOv11改进策略【卷积层】| 2024最新轻量级自适应提取模块 LAE 即插即用 保留局部信息和全局信息
一、本文介绍 本文记录的是利用轻量级自适应提取模块(LAE)模块优化YOLOv11的目标检测网络模型。LAE (Lightweight Adaptive Extraction) 在减少参数和计算成本的同时,能够提取更丰富语义信息的特征,克服了传统卷积方法难以捕捉全局信息的问题,并能更好地提取ROI特征。本文将…...

工作转型与个人突破提升:如何在社会浪潮中激流勇进
文章目录 一、写在前面二、技术人的迷茫三、做好项目经理其实很难四、从纯技术者转型为管理者面临的事五、最重要的技能【重磅推荐!免费简单内网穿透神器!支持linuxwindows】 一、写在前面 近期工作变动,虽然说对于开发者而言,工…...

mongodb:增删改查和特殊查询符号手册
前言 最近考虑开发游戏,网上推荐使用非关系数据库mongodb,因此浅尝了一番,并将一些语句和符号记录在这里。 相对于mysql、oracle这些关系型数据库,基于json文档的mongodb在很多地方都与之大不相同(可以类比为TCP握手连…...

你的Mac book多久没有清洁键盘屏幕了,Mac清洁好帮手来了
你的Mac book键盘使用时间长了不会打油吗,你的屏幕使用久了不会沾灰吗,那你还不清洁一下 你不清洁的原因,是怕清洁键盘误触发吗,还是怕屏幕擦不干净白擦,还是觉得每次都要睡眠或关机再清洁很麻烦 Cleaner是Mac的清洁…...

ANA基因组数据库(ANAgdb)
ANA进化阶由早期发育的被子植物谱系组成,包括无油樟目(Amborellales)、睡莲目(Nymphaeales)和木兰藤目(Austrobaileyales),在进化上具有重要地位。 ANA基因组数据库(ANA…...

leetcode 704 二分查找
704. 二分查找 已解答 简单 相关标签 相关企业 给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。 示例 1: 输入: nu…...
)
Vue学习笔记(十一)
一. Promise 1. 异步 异步:则是将耗时很长的A交付的工作交给系统之后,就去继续做B交付的工作,等到系统完成了前面的工作之后,再通过回调或者事件,继续做A剩下的工作。AB工作的完成顺序,和交付他们的时间顺…...

ABAP进阶学习1:动态内表1-通过系统表LVC_T_FCAT类型定义内表
动态内表1-通过系统表LVC_T_FCAT类型定义内表 如果对你有帮助,点个关注收藏吧~ 做BW做久了,突然对abap有了探索欲,开始进一步学习abap了,以后这个系列会逐步更新,欢迎小伙伴点个关注一起学习,我学习的方法…...

【Vispy库】一个用于高性能交互式2D/3D数据可视化库 Python库
Vispy库 1、你好,Vispy!2、安装Vispy,轻松上手3、案例一:绘制简单的2D图形4、案例二:3D图形的绘制5、案例三:大规模数据的可视化6、结语 1、你好,Vispy! Vispy是一个用于Python的高…...

为什么 C 语言数组是从 0 开始计数的?
C 语言等大多数编程语言的数组从 0 开始而不从 1 开始,有两个原因: 第一:地址计算更方便 C 语言从 0 开始的话,array[i] 的地址就正好是: (array i) 如果是从 1 开始的话,就是 (array i - 1) 多一次计…...

matlab线性度计算程序
matlab线性度计算程序 环境 matlab2023a ads2020 原理 其中f(v)是曲线,fmax是f(v)的最大值,fmin是f(v)的最小值,vmax为fmax对应v值,vmin为fmin对应v值。 L∆fmax/(fmax-fmin) (1) ∆fmaxmax[f(v)-[fmin-K*(v-vmin)]] (2) K(…...
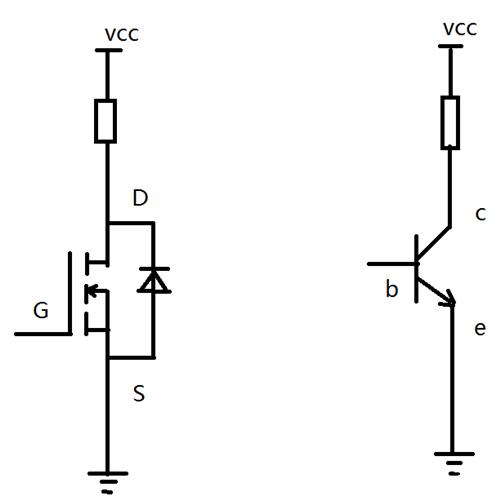
为什么NMOS管比PMOS管更受欢迎?
NMOS在实际应用中为何比PMOS要更受欢迎。本文将从导电沟道、电子迁移率和器件速度等多个方面来展开讲解。 首先是在性能方面考虑: 与NMOS管驱动能力相同的一个PMOS管,其器件面积可能是NMOS管的2~3倍,然而器件面积会影响导通电阻…...

【论文复现】短期电力负荷
作者主页: 七七的个人主页 文章收录专栏: 论文复现 欢迎大家点赞 👍 收藏 ⭐ 加关注哦!💖💖 短期电力负荷 论文发表问题背景一. 基本问题二. 本论文发现的问题 对于论文发现问题的解决方案:复现…...

pytest脚本常用的执行命令
pytest脚本常用的执行命令 一、一般执行的脚本,执行.py文件整个脚本二、执行.py文件脚本中的一个模块三、执行脚本,执行.py文件整个脚本,或则一个模块,查看对应的日志信息3.1.py文件执行allure的脚本3.2去dos框下去执行对应的脚本…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...

土建施工员考试:建筑施工技术重点知识有哪些?
《管理实务》是土建施工员考试中侧重实操应用与管理能力的科目,核心考查施工组织、质量安全、进度成本等现场管理要点。以下是结合考试大纲与高频考点整理的重点内容,附学习方向和应试技巧: 一、施工组织与进度管理 核心目标: 规…...

TJCTF 2025
还以为是天津的。这个比较容易,虽然绕了点弯,可还是把CP AK了,不过我会的别人也会,还是没啥名次。记录一下吧。 Crypto bacon-bits with open(flag.txt) as f: flag f.read().strip() with open(text.txt) as t: text t.read…...

js 设置3秒后执行
如何在JavaScript中延迟3秒执行操作 在JavaScript中,要设置一个操作在指定延迟后(例如3秒)执行,可以使用 setTimeout 函数。setTimeout 是JavaScript的核心计时器方法,它接受两个参数: 要执行的函数&…...

从0开始学习R语言--Day17--Cox回归
Cox回归 在用医疗数据作分析时,最常见的是去预测某类病的患者的死亡率或预测他们的结局。但是我们得到的病人数据,往往会有很多的协变量,即使我们通过计算来减少指标对结果的影响,我们的数据中依然会有很多的协变量,且…...
