企业SRC挖掘选择与信息收集指南
内容预览 ≧∀≦ゞ
- 企业SRC挖掘选择与信息收集指南
- 导语
- 1. 企业SRC的选择
- 2. 信息收集
- 2.1 集团与子公司
- 2.2 小程序与APP
- 2.3 Web端信息收集
- 3. 信息收集常用模板
- 总结
企业SRC挖掘选择与信息收集指南
导语
近年来,企业的安全响应中心(SRC)已逐渐成为白帽子与安全研究人员的关注重点,选择合适的企业SRC可以提高挖掘效率和收获回报。本文将详细介绍如何选择企业SRC、常见信息收集方法以及具体操作技巧。
1. 企业SRC的选择
选择企业SRC时,可以从以下几个方面进行考量:
- 英雄榜:查看企业SRC平台的英雄榜,关注总排行分数高且近三个月有白帽挖的SRC平台。通常,英雄榜上得分高、更新频繁的平台,往往意味着白帽提交漏洞活跃,奖励往往更为丰厚,适合优先选择。有时候,选择挖一些新上线的、小众的SRC可能更容易上榜,但同时需要权衡其漏洞评估机制和奖励体系的成熟度,因为这些SRC的评估和奖励机制往往不如大厂那么成熟。
- 礼品与奖励:不同SRC平台的奖励机制有所不同,且奖励水平与漏洞的严重程度挂钩。一些平台提供现金奖励或等值购物卡兑换,而一些平台只提供礼品兑换。可以先了解平台的奖励规则,合理评估时间与投入产出。建议优先选择奖励透明度和价值较高的SRC平台。
- 公告:企业SRC通常会发布公告,包括收录范围、奖励情况和最新政策更新。及时查看公告,了解当前支持挖掘的范围和漏洞奖励制度,以免因超出范围而不被采纳。同时,公告中的收录范围调整和漏洞奖励细节,能帮助白帽子精准定位当前可挖掘目标,提高挖掘效率。
- 活动:许多SRC平台定期开展漏洞挖掘活动,例如双倍积分或特定漏洞类别的额外奖励活动。这类活动能有效提升白帽子的参与兴趣,同时通过额外激励带来更丰厚的回报。因此,在选择SRC时,建议关注活动多、激励措施明确的平台,这类SRC更易于激励并回馈挖掘者,通常能帮助白帽子在短期内获得更多成就和收益。
2. 信息收集
信息收集是SRC挖掘的第一步,也是至关重要的环节。在选择好目标企业SRC后,深入信息收集将为后续漏洞挖掘提供扎实的基础。信息收集的范围可以分为以下几类:
2.1 集团与子公司
- 集团:许多大型企业会成立多个分支公司或子公司,因此集团下的子公司往往也纳入SRC的收录范围。可以通过官方渠道、财务报告或新闻稿了解该集团旗下的子公司信息。
- 子公司:子公司的安全性可能不如母公司,成为常见的攻击入口。在收集子公司信息时,需重点关注其主域、子域和产品应用。
2.2 小程序与APP
- 小程序:许多企业推出微信、支付宝等平台上的小程序,为用户提供便利服务。小程序通常和企业系统进行交互,但因其开发周期短,安全性相对较弱。可以通过分析接口、流量等方式收集小程序相关信息。
- APP:企业APP应用往往覆盖广泛,包含核心业务逻辑,成为白帽子的主要关注点。可以通过应用商店下载APP,使用静态、动态分析工具分析APP的通信数据、接口和资源文件。
2.3 Web端信息收集
Web端信息是最为直观的挖掘入口。Web端信息收集主要包括主域名、子域名、备案信息和图标等。以下是常用信息收集项:
- 主域:获取企业的主域名,并作为基础进行延展性的子域名挖掘。
- ICP备案:通过ICP备案信息可查询公司其他关联域名,有助于进一步扩展攻击面。
- 子域名:利用DNS查询和子域名扫描工具,查找企业的各类子域名,如内部管理系统、测试系统等。
- 域名:收集企业注册的各类域名,并筛选有价值的业务域名。可以通过Whois信息查询、企业官网及公开数据源获取。
- Icon:利用网站图标(icon)的hash值,能有效发现目标企业的隐藏服务和子域名。
3. 信息收集常用模板
信息收集可以根据预设模板,结构化地收集目标企业的各类信息。以下为常见信息收集模板:
- 集团/子公司:集团的安全政策和子公司之间可能存在安全差距,白帽子可以从母公司扩展至子公司进行挖掘。
- 小程序:分析小程序接口和数据交互点,发现业务逻辑漏洞或安全隐患。
- APP:下载并逆向分析APP应用,抓取API请求数据,排查不安全的通信或接口。
- 主域/子域名:以主域为基础,通过子域名扫描扩展更多入口,利用资产扫描工具可大幅提升效率。
- ICP备案:通过备案信息获取关联域名,有助于收集到更多潜在的业务系统。
- Icon:通过图标hash值反查,进一步扩大信息收集面。
总结
选择合适的企业SRC并进行有效的信息收集,将大幅提升漏洞挖掘的效率和准确性。在实际操作中,建议根据企业特点调整挖掘方法,结合模板收集不同系统信息,最终提升挖掘质量和收获。
最后,再次感谢您阅读本篇文章,如果您对文中内容有任何疑问或建议,欢迎在评论区与我交流!您的点赞和分享将是我继续创作的动力。
相关文章:

企业SRC挖掘选择与信息收集指南
内容预览 ≧∀≦ゞ 企业SRC挖掘选择与信息收集指南导语1. 企业SRC的选择2. 信息收集2.1 集团与子公司2.2 小程序与APP2.3 Web端信息收集 3. 信息收集常用模板总结 企业SRC挖掘选择与信息收集指南 导语 近年来,企业的安全响应中心(SRC)已逐渐…...

Golang | Leetcode Golang题解之第524题通过删除字母匹配到字典里最长单词
题目: 题解: func findLongestWord(s string, dictionary []string) (ans string) {m : len(s)f : make([][26]int, m1)for i : range f[m] {f[m][i] m}for i : m - 1; i > 0; i-- {f[i] f[i1]f[i][s[i]-a] i}outer:for _, t : range dictionary …...
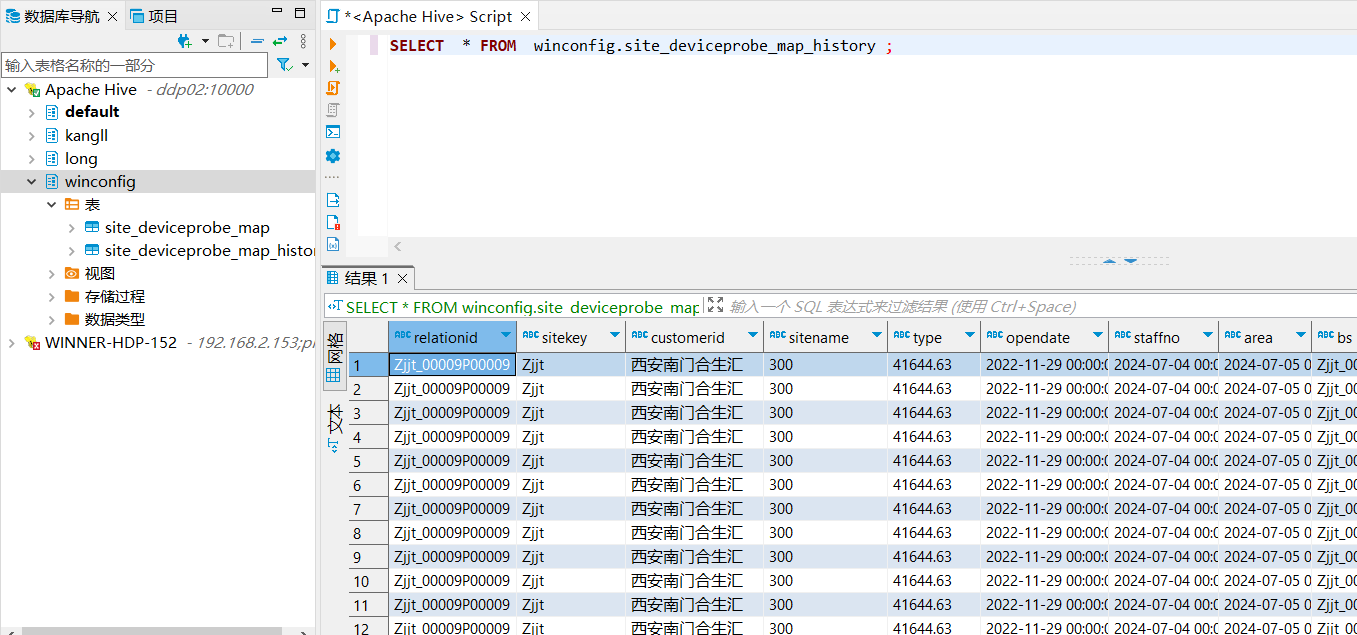
【DBeaver】连接带kerberos的hive[Apache|HDP]
目录 一、安装配置Kerberos客户端环境 1.1 安装Kerberos客户端 1.2 环境配置 二、基于Cloudera驱动创建连接 三、基于Hive原生驱动创建连接 一、安装配置Kerberos客户端环境 1.1 安装Kerberos客户端 在Kerberos官网下载,地址如下:https://web.mit.edu/kerberos…...
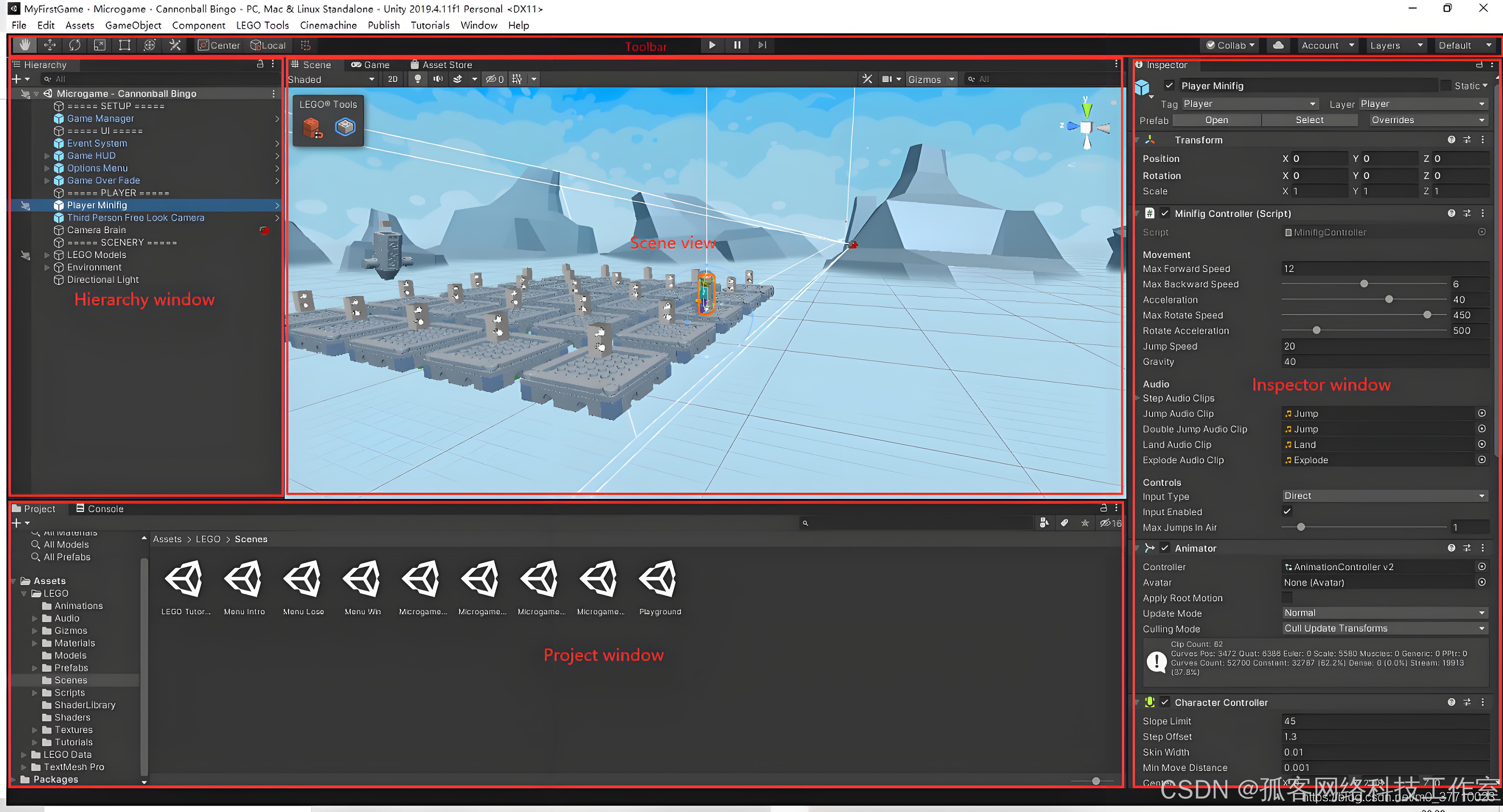
Unity3D 开发教程:从入门到精通
Unity3D 开发教程:从入门到精通 Unity3D 是一款强大的跨平台游戏引擎,广泛应用于游戏开发、虚拟现实、增强现实等领域。本文将详细介绍 Unity3D 的基本概念、开发流程以及一些高级技巧,帮助你从零基础到掌握 Unity3D 开发。 目录 Unity3D…...
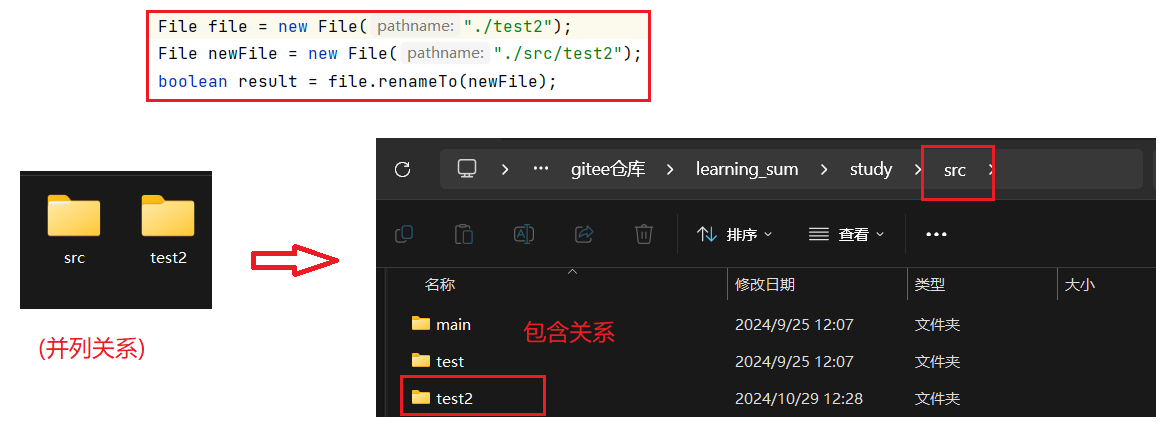
文件操作和 IO(一):文件基础知识 文件系统操作 => File类
目录 1. 什么是文件 1.1 概念 1.2 硬盘, 内存, 寄存器之间的区别 1.3 机械硬盘和固态硬盘 2. 文件路径 2.1 绝对路径 2.2 相对路径 3. 文件分类 4. File 类 4.1 属性 4.2 构造方法 4.3 方法 1. 什么是文件 1.1 概念 狭义上的文件: 保存在硬盘上的文件广义的上的文…...

用Pyhon写一款简单的益智类小游戏——2048
文字版——代码及讲解 代码—— import random# 初始化游戏棋盘 def init_board():return [[0] * 4 for _ in range(4)]# 在棋盘上随机生成一个2或4 def add_new_tile(board):empty_cells [(i, j) for i in range(4) for j in range(4) if board[i][j] 0]if empty_cells:i,…...
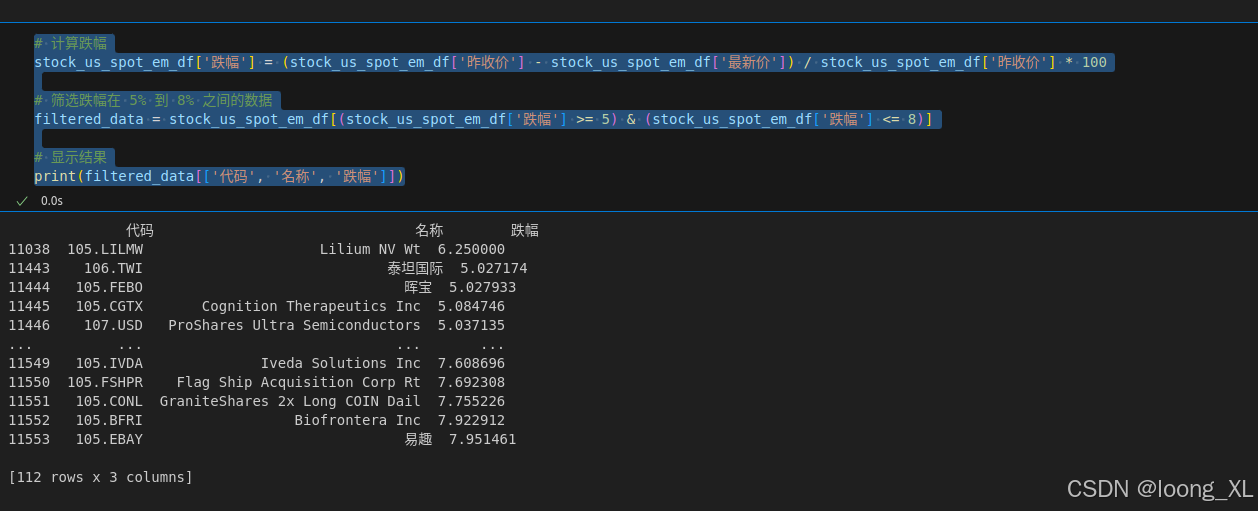
akshare股票涨跌幅自定义范围查询:A股、港股、美股
参看:https://stock.hexun.com/2024-10-31/215251914.html 涨幅计算公式:(当前价格 - 上一个交易日收盘价) 上一个交易日收盘价 100% 。 跌幅计算公式:(上一个交易日收盘价 - 当前价格) 上一个…...

通过js控制修改css变量
在JavaScript中,你可以通过操作CSS变量(也称为自定义属性)来动态改变样式。CSS变量在CSS中使用 – 前缀定义,例如 --main-color: red;。在JavaScript中,你可以使用 document.documentElement.style.setProperty 方法来…...
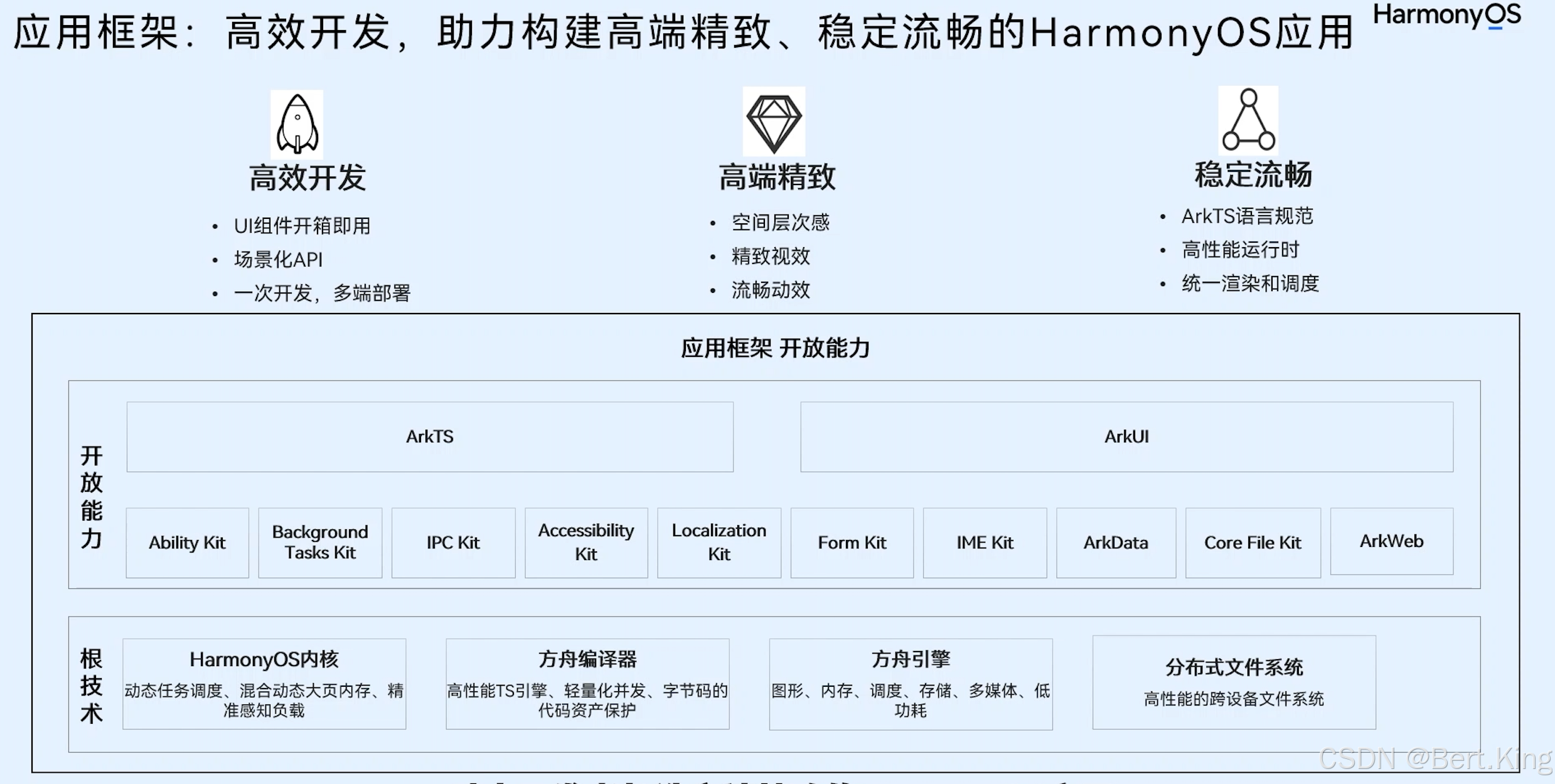
<HarmonyOS第一课>HarmonyOS SDK开放能力简介的课后习题
不出户,知天下; 不窥牖,见天道。 其出弥远,其知弥少。 是以圣人不行而知,不见而明,不为而成。 本篇<HarmonyOS第一课>HarmonyOS SDK开放能力简介是简单介绍了HarmonyOS SDK,不需要大家过多…...

深度学习:yolo的使用--图像处理
定义了一个名为 ListDataset 的类,它继承自 PyTorch 的 Dataset 类,这个数据集从一个包含图像文件路径的列表中读取图像和对应的标签文件 class ListDataset(Dataset):def __init__(self, list_path, img_size416, augmentTrue, multiscaleTrue, normalized_labelsT…...
:初始化、类型定义与函数使用)
TypeScript实用笔记(一):初始化、类型定义与函数使用
文章目录 一、ts初始化1. 初始化.json文件一2. 启动方式2.1 直接运行.ts文件2.2 转换运行 二、类型1. 参数类型1.1 常规参数1.2 symbol1.3 数组\[]1.4 元组\[]1.5 用字面量定义数据类型 2. Object3. 枚举类型\[Enum]3.1 数字枚举3.2 字符串枚举 三、 类型别名1. 数组别名使用2.…...
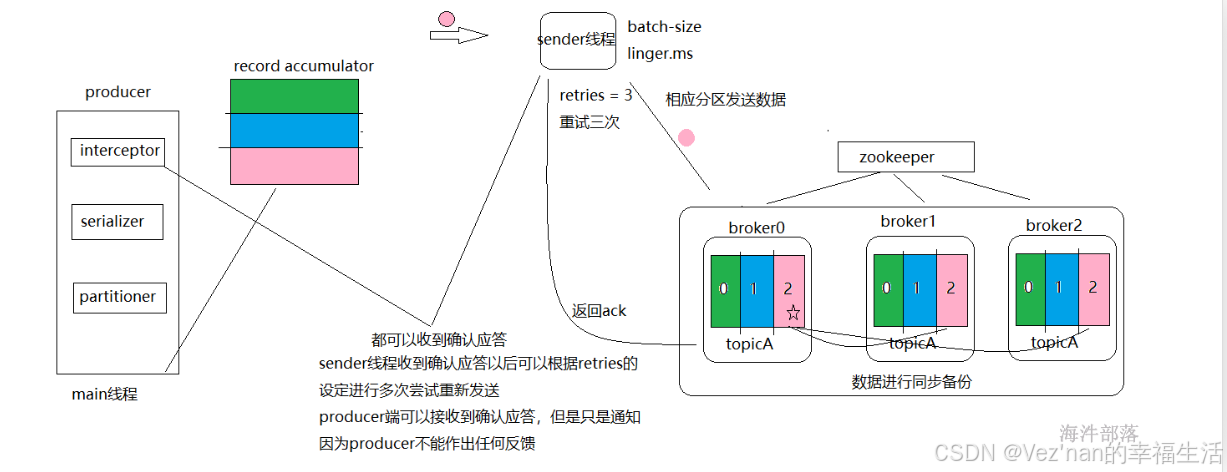
【大数据学习 | kafka】producer之拦截器,序列化器与分区器
1. 自定义拦截器 interceptor是拦截器,可以拦截到发送到kafka中的数据进行二次处理,它是producer组成部分的第一个组件。 public static class MyInterceptor implements ProducerInterceptor<String,String>{Overridepublic ProducerRecord<…...

零基础学西班牙语,柯桥专业小语种培训泓畅学校
No te comas el coco, seguro que te ha salido bien la entrevista. Ya te llamarn. 别瞎想了!我保证你的面试很顺利。他们会给你打电话的。 这里的椰子是"头"的比喻。在西班牙的口语中,我们也可以听到其他同义表达,比如&#x…...
)
C++学习:类和对象(三)
一、深入讲解构造函数 1. 什么是构造函数? 构造函数(Constructor)是在创建对象时自动调用的特殊成员函数,用于初始化对象的成员变量。构造函数的名称与类名相同,没有返回类型 2. 构造函数的类型 (1&…...
高阶数据结构--图(graph)
图(graph) 1.并查集1. 并查集原理2. 并查集实现3. 并查集应用 2.图的基本概念3. 图的存储结构3.1 邻接矩阵3.2 邻接矩阵的代码实现3.3 邻接表3.4 邻接表的代码实现 4. 图的遍历4.1 图的广度优先遍历4.2 广度优先遍历的代码 1.并查集 1. 并查集原理 在一…...
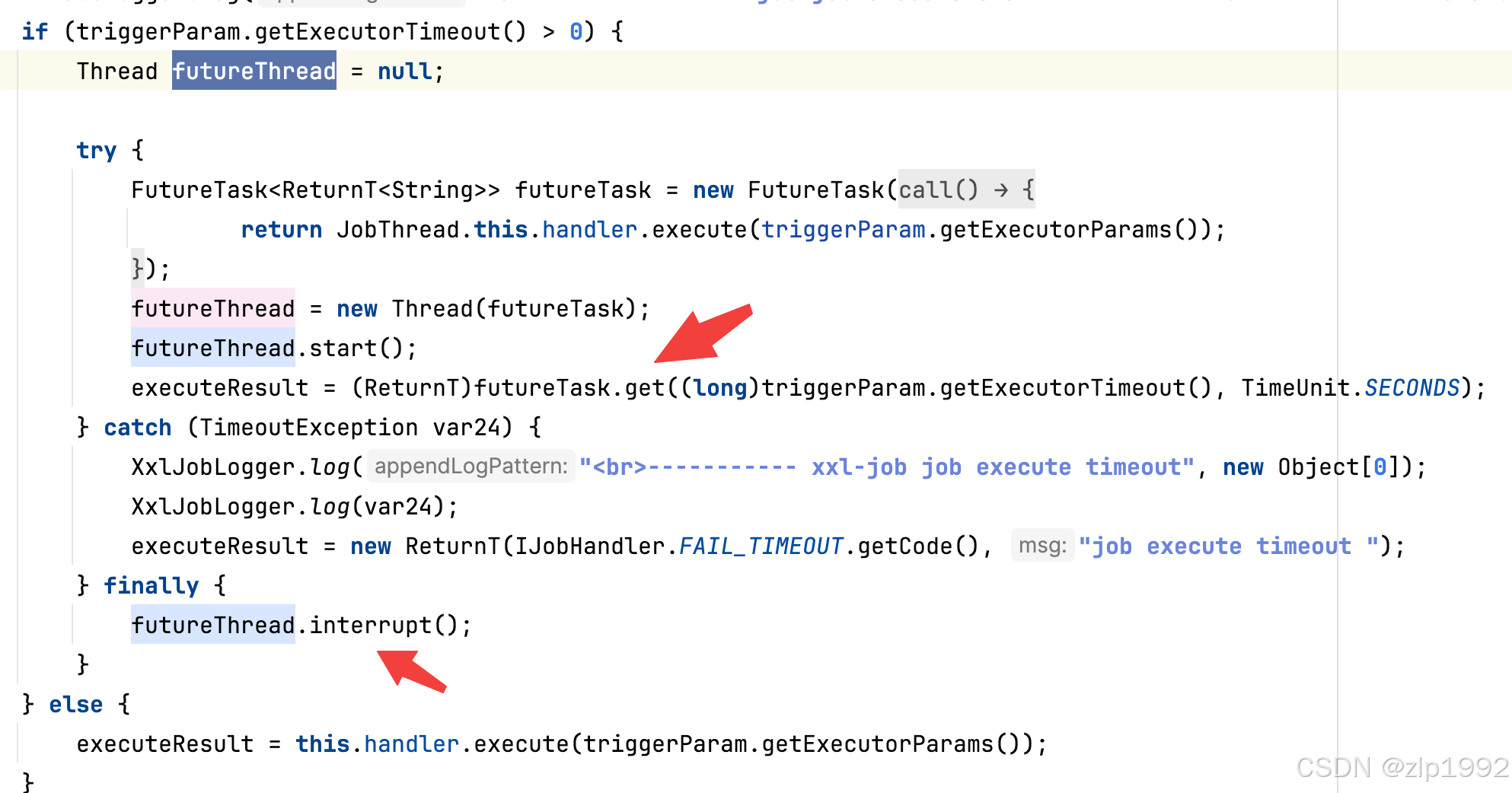
xxl-job java.sql.SQLException: interrupt问题排查
近期生产环境固定凌晨报错,提示 ConnectionManager [Thread-23069] getWriteConnection db:***,pattern: error, jdbcUrl: jdbc:mysql://***:3306/***?connectTimeout3000&socketTimeout180000&autoReconnecttrue&zeroDateTimeBehaviorCONVERT_TO_NUL…...
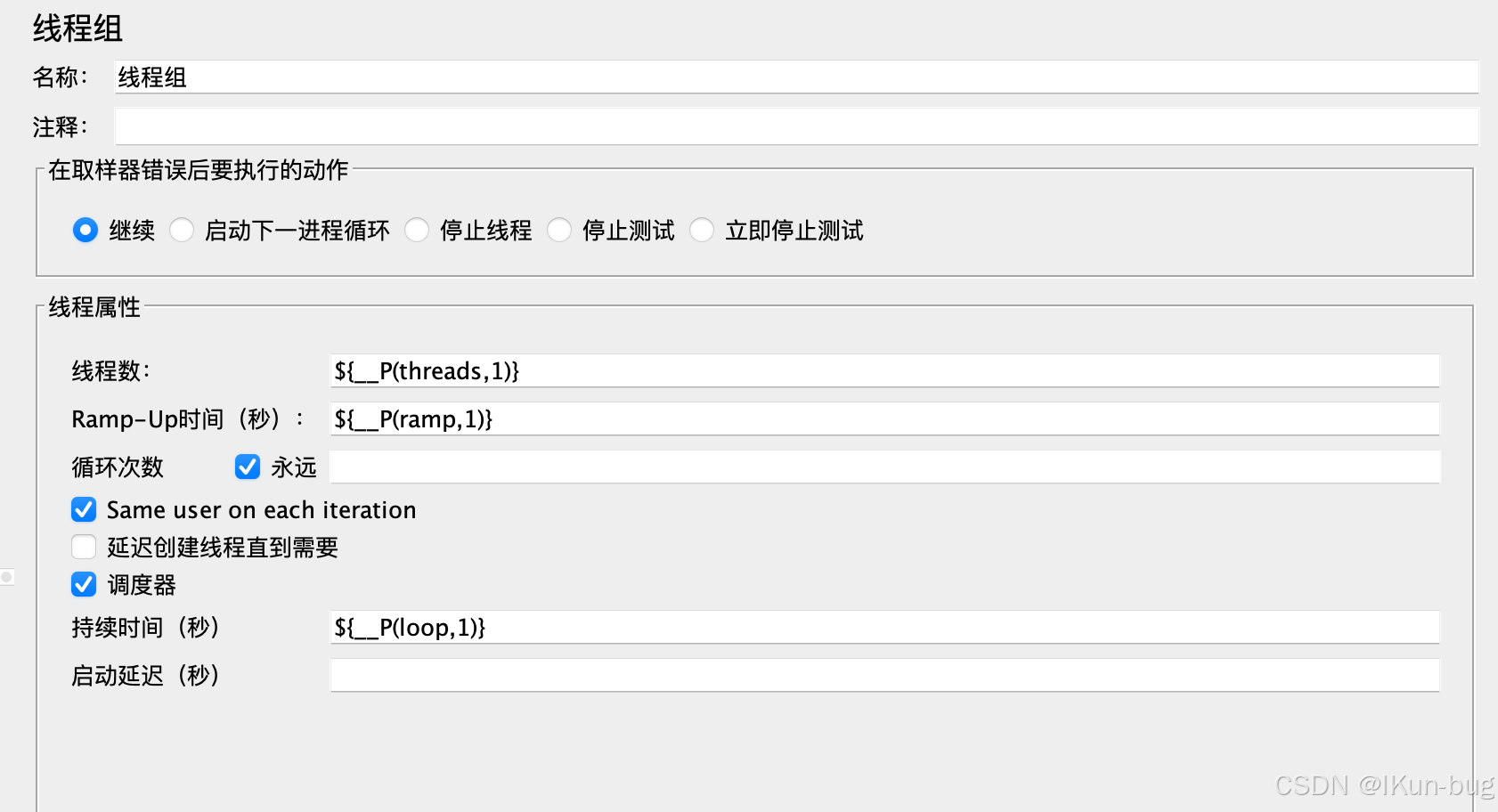
jmeter压测工具环境搭建(Linux、Mac)
目录 java环境安装 1、anaconda安装java环境(推荐) 2、直接在本地环境安装java环境 yum方式安装jdk 二进制方式安装jdk jmeter环境安装 1、jmeter单机安装 启动jmeter 配置环境变量 jmeter配置中文 2、jmeter集群搭建 多台机器部署jmeter集群…...

docker设置加速
sudo tee /etc/docker/daemon.json <<-‘EOF’ { “registry-mirrors”: [ “https://register.liberx.info”, “https://dockerpull.com”, “https://docker.anyhub.us.kg”, “https://dockerhub.jobcher.com”, “https://dockerhub.icu”, “https://docker.awsl95…...

使用requestAnimationFrame写防抖和节流
debounce.ts 防抖工具函数: function Animate() {this.timer null; }Animate.prototype.start function (fn) {if (!fn) {throw new Error(需要执行函数);}if (this.timer) {this.stop();}this.timer requestAnimationFrame(fn); }Animate.prototype.stop function () {i…...

Puppeteer 与浏览器版本兼容性:自动化测试的最佳实践
Puppeteer 支持的浏览器版本映射:从 v20.0.0 到 v23.6.0 自 Puppeteer v20.0.0 起,这个强大的自动化库开始支持与 Chrome 浏览器的无头模式和有头模式共享相同代码路径,为自动化测试带来了更多便利。从 v23.0.0 开始,Puppeteer 进…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...
