数列分块入门
本期是数列分块入门。其中的大部分题目来自hzwer在LOJ上提供的数列分块入门系列。
Blog:here (其实是对之前分块的 blog 的整理补充) sto hzwer orz %%% [转载]
------------------------------------------------------------------------------------------------------------------------
分块
我举个例子来说分块。
在一个学校里,有很多班级,而每一个班级就是一个块。
假设某天校长想知道一个班考试的总分,直接查询即可。那如果要查询 1 班的 30 号到 10 班的 20 号呢?对于完整的班级,直接查询;不完整的暴力。
那什么时候这个算法时间复杂度最低呢?答:当块的长度为时。
而这就是分块。
例题
LOJ-P6277:
我们每个元素个元素分为一块,共有
块,以及区间两侧的两个不完整的块。这两个不完整的块中至多
个元素。我们给每个块设置一个
(就是记录这个块中元素一起加了多少),每次操作对每个整块直接
标记,而不完整的块元素较少,暴力修改元素的值。
这样,每次询问时返回元素的值加上其所在块的加法标记即可。
时间复杂度。根据均值不等式,当
取
时总复杂度最低。
#include <bits/stdc++.h>
using namespace std;
const int maxn=50005;
int a[maxn],idx[maxn],tag[maxn],tot;
void change(int l,int r,int c){for(int i=l;i<=min(idx[l]*tot,r);i++)a[i]+=c;if(idx[l]!=idx[r]){for(int i=(idx[r]-1)*tot+1;i<=r;i++)a[i]+=c;}for(int i=idx[l]+1;i<=idx[r]-1;i++)tag[i]+=c;
}
int main(){int n;cin>>n;tot=sqrt(n);for(int i=1;i<=n;i++)cin>>a[i];for(int i=1;i<=n;i++)idx[i]=(i-1)/tot+1;for(int i=1;i<=n;i++){int opt,l,r,c;cin>>opt>>l>>r>>c;if(opt==0)change(l,r,c);if(opt==1)cout<<a[r]+tag[idx[r]]<<endl;}return O;
}LOJ-P6278:
我们先来思考只有询问操作的情况,不完整的块枚举统计即可;而要在每个整块内寻找小于一个值的元素数,于是我们不得不要求块内元素是有序的,这样就能使用二分法对块内查询,需要预处理时每块做一遍排序,复杂度,每次查询在
个块内二分,以及暴力
个元素,总复杂度
。
那么区间加怎么办呢?套用第一题的方法,维护一个加法标记,略有区别的地方在于,不完整的块修改后可能会使得该块内数字乱序,所以头尾两个不完整块需要重新排序。在加法标记下的询问操作,块外还是暴力,查询小于的元素个数,块内用
作为二分的值即可。
#include <bits/stdc++.h>
using namespace std;
const int maxn=50005;
int a[maxn],idx[maxn],tag[maxn],tot,n;
vector<int> block[505];
void reset(int x){block[x].clear();for(int i=(x-1)*tot+1;i<=min(x*tot,n);i++)block[x].push_back(a[i]);sort(block[x].begin(),block[x].end());
}
void change(int l,int r,int c){for(int i=l;i<=min(idx[l]*tot,r);i++)a[i]+=c;reset(idx[l]);if(idx[l]!=idx[r]){for(int i=(idx[r]-1)*tot+1;i<=r;i++)a[i]+=c;reset(idx[r]);}for(int i=idx[l]+1;i<=idx[r]-1;i++)tag[i]+=c;
}
int query(int l,int r,int c){int ans=0;for(int i=l;i<=min(idx[l]*tot,r);i++){if(a[i]+tag[idx[l]]<c)ans++;}if(idx[l]!=idx[r]){for(int i=(idx[r]-1)*tot+1;i<=r;i++){if(a[i]+tag[idx[r]]<c)ans++;}}for(int i=idx[l]+1;i<=idx[r]-1;i++)ans+=lower_bound(block[i].begin(),block[i].end(),c-tag[i])-block[i].begin();return ans;
}
int main(){cin>>n;tot=sqrt(n);for(int i=1;i<=n;i++)cin>>a[i];for(int i=1;i<=n;i++){idx[i]=(i-1)/tot+1;block[idx[i]].push_back(a[i]);}for(int i=1;i<=idx[n];i++)sort(block[i].begin(),block[i].end());for(int i=1;i<=n;i++){int opt,l,r,c;cin>>opt>>l>>r>>c;if(opt==0)change(l,r,c);if(opt==1)cout<<query(l,r,c*c)<<endl;}return O;
}LOJ-P6279:
接着第二题的解法,其实只要把块内查询的二分稍作修改即可。
不过这题其实想表达:可以在块内维护其它结构使其更具有拓展性,比如放一个set,这样如果还有插入、删除元素的操作,会更加的方便。
#include <bits/stdc++.h>
using namespace std;
const int maxn=10000S;
int a[maxn],idx[maxn],tag[maxn],tot=1000;
set<int> st[10S];
void change(int l,int r,int c){for(int i=l;i<=min(idx[l]*tot,r);i++){st[idx[l]].erase(a[i]);a[i]+=c;st[idx[l]].insert(a[i]);}if(idx[l]!=idx[r]){for(int i=(idx[r]-1)*tot+1;i<=r;i++){st[idx[r]].erase(a[i]);a[i]+=c;st[idx[r]].insert(a[i]);}}for(int i=idx[l]+1;i<=idx[r]-1;i++)tag[i]+=c;
}
int query(int l,int r,int c){int ans=-1;for(int i=l;i<=min(idx[l]*tot,r);i++){int val=a[i]+tag[idx[l]];if(val<c)ans=max(val,ans);}if(idx[l]!=idx[r]){ for(int i=(idx[r]-1)*tot+1;i<=r;i++){int val=a[i]+tag[idx[r]];if(val<c)ans=max(val,ans);}}for(int i=idx[l]+1;i<=idx[r]-1;i++){int x=c-tag[i];set<int>::iterator itr=st[i].lower_bound(x);if(itr==st[i].begin())continue;--itr;ans=max(ans,*itr+tag[i]);}return ans;
}
int main(){int n;cin>>n;for(int i=1;i<=n;i++)cin>>a[i]; for(int i=1;i<=n;i++){idx[i]=(i-1)/tot+1;st[idx[i]].insert(a[i]);}for(int i=1;i<=n;i++){int opt,l,r,c;cin>>opt>>l>>r>>c;if(opt==0)change(l,r,c);if(opt==1)cout<<query(l,r,c)<<endl;}return 0;
}LOJ-P6280:
这题的询问变成了区间上的询问,不完整的块还是暴力;而要想快速统计完整块的答案,需要维护每个块的元素和,先要预处理一下。
考虑区间修改操作,不完整的块直接改,顺便更新块的元素和;完整的块类似之前标记的做法,直接根据块的元素和所加的值计算元素和的增量。
#include <bits/stdc++.h>
using namespace std;
int idx[50005],tot;
long long a[50005],tag[50005],sum[50005];
void change(int l,int r,int c){for(int i=l;i<=min(idx[l]*tot,r);i++){a[i]+=c;sum[idx[l]]+=c;}if(idx[l]!=idx[r]){for(int i=(idx[r]-1)*tot+1;i<=r;i++){a[i]+=c;sum[idx[r]]+=c;}}for(int i=idx[l]+1;i<=idx[r]-1;i++)tag[i]+=c;
}
long long query(int l,int r){long long ans=0;for(int i=l;i<=min(idx[l]*tot,r);i++)ans+=a[i]+tag[idx[l]];if(idx[l]!=idx[r]){for(int i=(idx[r]-1)*tot+1;i<=r;i++)ans+=a[i]+tag[idx[r]];}for(int i=idx[l]+1;i<=idx[r]-1;i++)ans+=sum[i]+tot*tag[i];return ans;
}
int main(){int n;cin>>n;tot=sqrt(n);for(int i=1;i<=n;i++)cin>>a[i];for(int i=1;i<=n;i++){idx[i]=(i-1)/tot+1;sum[idx[i]]+=a[i];}for(int i=1;i<=n;i++){int opt,l,r,c;cin>>opt>>l>>r>>c; if(opt==O)change(l,r,c);if(opt==1)cout<<query(l,r)%(c+1)<<endl;}return 0;
}LOJ-P6281:
稍作思考可以发现,开方操作比较棘手,主要是对于整块开方时,必须要知道每一个元素,才能知道他们开方后的和,也就是说,难以快速对一个块信息进行更新。
看来我们要另辟蹊径。不难发现,这题的修改就只有下取整开方,而一个数经过几次开方之后,它的值就会变成或者
。
如果每次区间开方只不涉及完整的块,意味着不超过个元素,直接暴力即可。
如果涉及了一些完整的块,这些块经过几次操作以后就会都变成或
,于是我们采取一种分块优化的暴力做法,只要每个整块暴力开方后,记录一下元素是否都变成了
或
,区间修改时跳过那些全为
或
的块即可。
这样每个元素至多被开方不超过次,显然复杂度没有问题。
#include <bits/stdc++.h>
using namespace std;
int a[50005],sum[50005],idx[50005],tot;
bool flag[50005];
void solve(int x){if(flag[x])return;flag[x]=1;sum[x]=0;for(int i=(x-1)*tot+1;i<=x*tot;i++){a[i]=sqrt(a[i]);sum[x]+=a[i];if(a[i]>1)flag[x]=0;}
}
void change(int l,int r,int c){for(int i=l;i<=min(idx[l]*tot,r);i++){sum[idx[l]]-=a[i];a[i]=sqrt(a[i]);sum[idx[l]]+=a[i];}if(idx[l]!=idx[r]){for(int i=(idx[r]-1)*tot+1;i<=r;i++){sum[idx[r]]-=a[i];a[i]=sqrt(a[i]);sum[idx[r]]+=a[i];}}for(int i=idx[l]+1;i<=idx[r]-1;i++)solve(i);
}
int query(int l,int r){int ans=0;for(int i=l;i<=min(idx[l]*tot,r);i++)ans+=a[i];if(idx[l]!=idx[r]){for(int i=(idx[r]-1)*tot+1;i<=r;i++)ans+=a[i];}for(int i=idx[l]+1;i<=idx[r]-1;i++)ans+=sum[i];return ans;
}
int main(){int n;cin>>n;tot=sqrt(n);for(int i=1;i<=n;i++)cin>>a[i];for(int i=1;i<=n;i++){idx[i]=(i-1)/tot+1;sum[idx[i]]+=a[i];}for(int i=1;i<=n;i++){int opt,l,r,c;cin>>opt>>l>>r>>c;if(opt==0)change(l,r,c);if(opt==l)cout<<query(l,r)<<endl;}return 0;
}LOJ-P6284:
区间修改没有什么难度,这题难在区间查询比较奇怪,因为权值种类比较多,似乎没有什么好的维护方法。
模拟一些数据可以发现,询问后一整段都会被修改,几次询问后数列可能只剩下几段不同的区间了。
我们思考这样一个暴力,还是分块,维护每个分块是否只有一种权值,区间操作的时候,对于同权值的一个块就统计答案,否则暴力统计答案,并修改标记,不完整的块也暴力。
这样看似最差情况每次都会耗费的时间,但其实可以这样分析:
假设初始序列都是同一个值,那么查询是,如果这时进行一个区间操作,它最多破坏首尾2个块的标记,所以只能使后面的询问至多多2个块的暴力时间,所以均摊每次操作复杂度还是
。换句话说,要想让一个操作耗费
的时间,要先花费
个操作对数列进行修改。初始序列不同值,经过类似分析后,就可以放心的暴力啦。
#include <bits/stdc++.h>
using namespace std;
int a[maxn],block[maxn],tag[maxn],n,s;
void reset(int x){if(tag[x]==-1)return;for(int i=(x-1)*s+1;i<=s*x;i++)a[i]=tag[x];tag[x]=-1;
}
int query(int l,int r,int c){ int ans=0;reset(block[l]);for(int i=l;i<=min(block[l]*s,r);i++){if(a[i]!=c)a[i]=c;elseans++;}if(block[l]!=block[r]){reset(block[r]);for(int i=(block[r]-1)*s+1;i<=r;i++){if(a[i]!=c)a[i]=c;elseans++;}}for(int i=block[l]+1;i<=block[r]-1;i++){if(tag[i]!=-1){if(tag[i]!=c)tag[i]=c;elseans+=s;}else{for(int j=(i-1)*s+1;j<=i*s;j++){if(a[j]!=c)a[j]=c;elseans++;}tag[i]=c;}}return ans;
}
int main(){memset(tag,-1,sizeof(tag));int n;cin>>n;s=sqrt(n);for(int i=1;i<=n;i++)cin>>a[i];for(int i=1;i<=n;i++)block[i]=(i-1)/s+1;for(int i=1;i<=n;i++){int l,r,c;cin>>l>>r>>c;cout<<query(l,r,c)<<endl;}return 0;
}HDU 5057:
分块板题。
#include <bits/stdc++.h>
using namespace std;
const int maxn=100005;
int v[maxn][15],tag[320][15][15],a[maxn];
void update(int x,int y,int z){for(int d=1;d<=10;d++){v[x][d]=y%10;tag[x/S][d][y%10]+=z;y/=10;}
}
int query(int l,int r,int d,int p){int L=l/S,R=r/S,res=0;if(L==R){for(int i=l;i<=r;i++)res+=(v[i][d]==p);}else{for(int i=l;i<(L+1)*S;i++)res+=(v[i][d]==p);for(int i=R*S;i<=r;i++)res+=(v[i][d]==p);for(int i=L+1;i<R;i++)res+=tag[i][d][p];}return res;
}
int main(){int t;cin>>t;while(t--){memset(tag,0,sizeof(tag));memset(v,0,sizeof(v));int n,m;cin>>n>>m;S=sqrt(n);for(int i=1;i<=n;i++){cin>>a[i];update(i,a[i],1);}while(m--){char op;cin>>op;if(op=='S'){int x,y;cin>>x>>y;update(x,a[x],-1);update(x,y,1);a[x]=y;}else{int l,r,d,p;cin>>l>>r>>d>>p;cout<<query(l,r,d,p)<<endl;}}}return 0;
}友情提醒:不要Ctrl C+Ctrl V
相关文章:
数列分块入门
本期是数列分块入门。其中的大部分题目来自hzwer在LOJ上提供的数列分块入门系列。 Blog:here (其实是对之前分块的 blog 的整理补充) sto hzwer orz %%% [转载] ---------------------------------------------------------------------------------…...

SPRD Android 14 Launcher 3 中添加长按桌面图标启动自由窗口模式功能
本文将介绍如何在SPRD Android 14 Launcher 3 中实现一个功能,使用户可以通过长按应用图标来启动自由窗口模式。这一功能的实现将提升多任务处理能力和应用使用体验。 修改的文件列表 以下是主要涉及的文件及其修改内容: QuickstepLauncher.java:添加自由窗口快捷方式的支…...

WebSocket详解:从前端到后端的全栈理解
文章目录 前言一、WebSocket简介1.1 WebSocket的特点 二、WebSocket的工作原理2.1 握手过程2.2 数据传输 三、WebSocket在前端的应用四、WebSocket在后端的应用五、WebSocket的局限与解决方案结语 前言 随着互联网技术的发展,传统的HTTP协议在某些场景下的局限性逐…...

SOLIDWORKS 2025加快装配体设计 确保可制造性
在快速变化的制造业环境中,SOLIDWORKS作为一款CAD软件,始终致力于提供有效、智能且可靠的解决方案,以满足设计师和工程师对装配体设计的多样化需求。随着SOLIDWORKS 2025版本的发布,其在加快装配体设计、确保可制造性方面取得了显…...

简单题:计算从位置 x 到 y 的最少步数| 豆包MarsCode AI刷题
题目解析:计算从位置 x 到 y 的最少步数 题目描述 题目要求从整数位置 x 移动到整数位置 y,每一步可以将当前位置增加或减少,且每步的增加或减少的值必须是连续的整数。首末两步的步长必须是 1。要求求出从 x 到 y 的最少步数。 思路分析 …...

HTML 基础标签——表单标签<form>
文章目录 1. `<form>` 标签:定义表单容器2. `<input>` 标签:多用途输入控件3. `<textarea>` 标签:多行文本输入框4. `<select>` 标签:下拉选择框5. `<option>` 标签:下拉菜单选项6. `<button>` 标签:按钮元素7. `<label>` 标签…...

LeetCode 每日一题 2024/10/28-2024/11/3
记录了初步解题思路 以及本地实现代码;并不一定为最优 也希望大家能一起探讨 一起进步 目录 10/28 685. 冗余连接 II10/29 3211. 生成不含相邻零的二进制字符串10/30 3216. 交换后字典序最小的字符串10/31 3165. 不包含相邻元素的子序列的最大和11/1 3259. 超级饮料…...

基于Spring Boot和Vue的电子商城系统功能设计
基于Spring Boot和Vue的电子商城系统功能设计 该系统是一个基于Spring Boot和Vue框架的电子商城平台,包含前台商城和后台管理系统。系统功能设计包括用户购物体验和管理员管理功能,支持商品的分类展示、收藏、购物车和订单管理等模块。以下是系统功能的简…...

成都睿明智科技有限公司正规吗靠谱吗?
在这个短视频风起云涌的时代,抖音电商以其独特的魅力,成为了无数商家竞相追逐的新蓝海。而在这片浩瀚的商海中,成都睿明智科技有限公司犹如一艘装备精良的航船,引领着众多企业破浪前行,探索抖音电商的无限可能。今天&a…...

【天线&化学】航拍图屋顶异常检测系统源码&数据集全套:改进yolo11-ContextGuided
改进yolo11-ContextGuided等200全套创新点大全:航拍图屋顶异常检测系统源码&数据集全套 1.图片效果展示 项目来源 人工智能促进会 2024.11.01 注意:由于项目一直在更新迭代,上面“1.图片效果展示”和“2.视频效果展示”展示的系…...

【回忆】JavaScript 中的 Map 有哪些方法
在 JavaScript 中,Map 对象是一种键值对的集合,类似于对象,但“键”可以是任何数据类型(对象或原始值)。Map 提供了多种方法来操作这些键值对。以下是 Map 对象的一些常用方法: 创建和初始化 new Map(): …...

Chrome与夸克的安全性对比
在当今数字化时代,浏览器的安全性对于用户来说至关重要。Chrome和夸克作为两款流行的浏览器,各有其特点和优势。本文将对这两款浏览器的安全性进行详细对比,帮助用户更好地了解它们之间的差异。(本文由https://www.chromegw.com/的…...

使用Python可视化支持向量机(SVM)
支持向量机(SVM)是用于分类和回归任务的强大监督学习模型。它们受欢迎背后的一个关键因素是它们有效处理线性和非线性数据的能力。在本文中,我们将探索使用Python和流行的库(如scikit-learn和Matplotlib)可视化SVM。 …...

C++泛型编程
一、什么是泛型编程 泛型编程 是一种编程范式,它通过编写可以处理多种数据类型的代码来实现代码的灵活复用。泛型编程主要通过模板来实现。 比如我们日常使用的容器类型vector就应用了模板来实现其通用性,我们在使用时可以通过传入型别创建对应的动态数…...
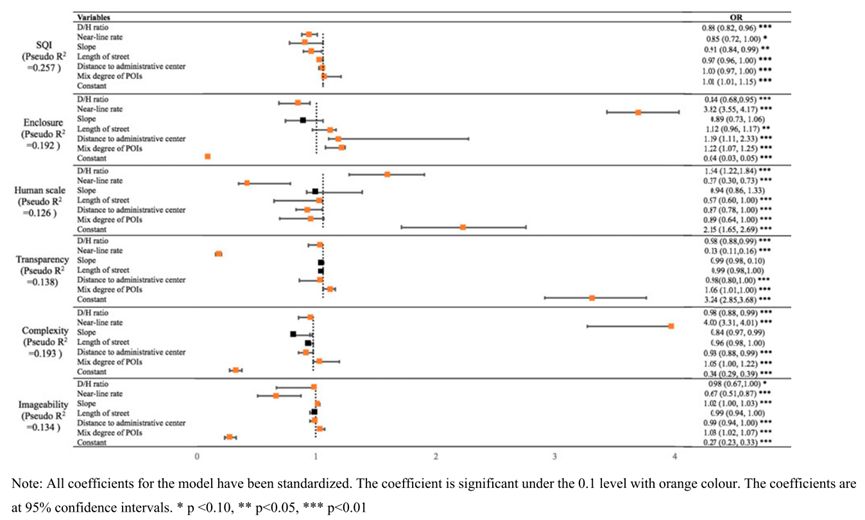
【论文分享】利用大量街景图片研究街道空间质量与建筑环境属性之间的关联
本研究通过有序逻辑回归模型,结合街景图片和街道数据,分析了街道空间质量与建筑环境属性的关系。通过Kappa分析和相关性分析,确定了影响街道空间质量的因素,并绘制了质量分布图。这些因素与街道质量的不同维度相关联,对…...

【Linux第七课--基础IO】内存级文件、重定向、缓冲区、文件系统、动态库静态库
目录 引入内存级文件重新使用C文件接口 -- 对比重定向写文件读文件文件流 认识文件操作的系统接口open参数 -- flagflag的内容宏的传参方式 open关闭文件写文件读文件结论 引入文件描述符fd、对文件的理解理解一切皆文件方法集文件fd的分配规则 重定向代码的重定向输入重定向输…...

对比C/C++语言,Rust语言有什么优势?
Rust语言相较于C/C语言有以下几个主要优势: 1. 内存安全:Rust通过其所有权系统和借用规则在编译时捕获许多常见的内存安全错误,如空指针引用和数据竞争,避免了许多常见的安全漏洞。这与C/C不同,后者通常需要手动管理内…...

Rust语言有哪些数据类型?
Rust语言的数据类型主要包括以下几种: 一、基本数据类型 1. 整数类型 i8, i16, i32, i64, i128: 有符号整数 u8, u16, u32, u64, u128: 无符号整数 isize, usize: 根据平台选择大小的整数(通常用于指针和索引) 2. 浮点数类型 f32: 32位浮…...

【论文笔记】Attention Prompting on Image for Large Vision-Language Models
🍎个人主页:小嗷犬的个人主页 🍊个人网站:小嗷犬的技术小站 🥭个人信条:为天地立心,为生民立命,为往圣继绝学,为万世开太平。 基本信息 标题: Attention Prompting on I…...

VScode设置系统界面字体
现象: 系统界面字体太大,导致菜单栏字体显示不全,每次使用都要先点然后才能打开终端和帮助 缩小字体应该就可以实现全部都看到的效果 步骤 Window: Zoom Level 调整所有窗口的默认缩放级别。大于“0”的每个增量(例如“1”&…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...
