简单题:计算从位置 x 到 y 的最少步数| 豆包MarsCode AI刷题
题目解析:计算从位置 x 到 y 的最少步数
题目描述
题目要求从整数位置 x 移动到整数位置 y,每一步可以将当前位置增加或减少,且每步的增加或减少的值必须是连续的整数。首末两步的步长必须是 1。要求求出从 x 到 y 的最少步数。
思路分析
首先,这个问题可以看作是在一个数轴上从 x 点移动到 y 点的问题。每一步的移动范围是上一步的 -1,+0 或 +1,且首尾两步的步长必须是 1。
我们可以从以下几个方面进行分析:
-
绝对距离与步数关系:
- 绝对距离
d = |y - x|决定了至少需要多少步。 - 由于每一步最多可以增加或减少前一步的步长+1,因此可以通过不断增加步长来覆盖整个距离。
- 绝对距离
-
步长变化:
- 步长从 1 开始,每一步的步长变化为 +1、-1 或 0。
- 由于首尾步长必须是 1,我们可以理解为在中间的步数中,我们可以选择增加步长来覆盖更多距离,也可以选择减小步长来灵活调整位置。
-
贪心策略:
- 在每一步中,为了尽快覆盖剩余的距离,我们希望尽量使用较大的步长。
- 但在某些情况下,为了最终能够精确到达 y 点,我们可能需要减小步长来调整位置。
代码详解
代码中使用了一个 sum 方法来计算从 1 到某个数的和,这是为了确定在给定的步长下,能够覆盖的最大距离。
public class Main {// 计算从 1 到 x 的和public static int sum(int x) {if (x <= 0) {return 0;}int res = 0;for (int i = 1; i <= x; i++) {res += i;}return res;}// 计算从 x 到 y 的最小步数public static int solution(int x, int y) {// 确保 x < y,便于处理if (x > y) {int temp = x;x = y;y = temp;}int l = 0, r = y - x;int step = 0;int stepDistance = 0;while (l < r) {if (step == 0) {stepDistance = 1;step = 1;l += stepDistance;continue;}int step1 = stepDistance + 1;int step2 = stepDistance;int step3 = stepDistance - 1;// 尝试使用最大步长 step1if (l + step1 < r) {int m = l + step1;int s = sum(step1 - 1);if ((r - m) >= s) {l = m;step++;stepDistance = step1;continue;}}// 尝试使用当前步长 step2if (l + step2 <= r) {int m = l + step2;int s = sum(step2 - 1);if ((r - m) >= s) {l = m;step++;stepDistance = step2;continue;}}// 尝试使用减小步长 step3if (l + step3 <= r) {int m = l + step3;int s = sum(step3 - 1);if ((r - m) >= s) {l = m;step++;stepDistance = step3;continue;}}}return step;}public static void main(String[] args) {// 测试用例System.out.println(solution(6, 7) == 1); // 输出 trueSystem.out.println(solution(12, 6) == 4); // 输出 trueSystem.out.println(solution(34, 45) == 6); // 输出 trueSystem.out.println(solution(50, 30) == 8); // 输出 true}
}
个人思考与分析
这个问题实际上是一个动态规划问题的简化版,由于步长的变化特性,使得我们可以使用贪心策略来求解。
-
贪心策略的优势:
- 在每一步中,选择最大可能的步长,可以尽快减少剩余的距离。
- 通过调整步长来适应最终位置的需求,确保最终能够精确到达 y 点。
-
代码优化:
- 在计算
sum方法时,可以使用数学公式n * (n + 1) / 2来优化,减少循环计算。 - 可以进一步简化代码,通过一些数学推导减少不必要的计算。
- 在计算
-
复杂度分析:
- 这个问题的时间复杂度主要取决于
while循环的次数,即步数的多少。 - 空间复杂度较低,主要是一些变量的存储。
- 这个问题的时间复杂度主要取决于
通过这道题目,我们可以更深入地理解贪心算法在实际问题中的应用,以及如何通过数学推导和算法优化来解决问题。
相关文章:

简单题:计算从位置 x 到 y 的最少步数| 豆包MarsCode AI刷题
题目解析:计算从位置 x 到 y 的最少步数 题目描述 题目要求从整数位置 x 移动到整数位置 y,每一步可以将当前位置增加或减少,且每步的增加或减少的值必须是连续的整数。首末两步的步长必须是 1。要求求出从 x 到 y 的最少步数。 思路分析 …...

HTML 基础标签——表单标签<form>
文章目录 1. `<form>` 标签:定义表单容器2. `<input>` 标签:多用途输入控件3. `<textarea>` 标签:多行文本输入框4. `<select>` 标签:下拉选择框5. `<option>` 标签:下拉菜单选项6. `<button>` 标签:按钮元素7. `<label>` 标签…...

LeetCode 每日一题 2024/10/28-2024/11/3
记录了初步解题思路 以及本地实现代码;并不一定为最优 也希望大家能一起探讨 一起进步 目录 10/28 685. 冗余连接 II10/29 3211. 生成不含相邻零的二进制字符串10/30 3216. 交换后字典序最小的字符串10/31 3165. 不包含相邻元素的子序列的最大和11/1 3259. 超级饮料…...

基于Spring Boot和Vue的电子商城系统功能设计
基于Spring Boot和Vue的电子商城系统功能设计 该系统是一个基于Spring Boot和Vue框架的电子商城平台,包含前台商城和后台管理系统。系统功能设计包括用户购物体验和管理员管理功能,支持商品的分类展示、收藏、购物车和订单管理等模块。以下是系统功能的简…...

成都睿明智科技有限公司正规吗靠谱吗?
在这个短视频风起云涌的时代,抖音电商以其独特的魅力,成为了无数商家竞相追逐的新蓝海。而在这片浩瀚的商海中,成都睿明智科技有限公司犹如一艘装备精良的航船,引领着众多企业破浪前行,探索抖音电商的无限可能。今天&a…...

【天线&化学】航拍图屋顶异常检测系统源码&数据集全套:改进yolo11-ContextGuided
改进yolo11-ContextGuided等200全套创新点大全:航拍图屋顶异常检测系统源码&数据集全套 1.图片效果展示 项目来源 人工智能促进会 2024.11.01 注意:由于项目一直在更新迭代,上面“1.图片效果展示”和“2.视频效果展示”展示的系…...

【回忆】JavaScript 中的 Map 有哪些方法
在 JavaScript 中,Map 对象是一种键值对的集合,类似于对象,但“键”可以是任何数据类型(对象或原始值)。Map 提供了多种方法来操作这些键值对。以下是 Map 对象的一些常用方法: 创建和初始化 new Map(): …...

Chrome与夸克的安全性对比
在当今数字化时代,浏览器的安全性对于用户来说至关重要。Chrome和夸克作为两款流行的浏览器,各有其特点和优势。本文将对这两款浏览器的安全性进行详细对比,帮助用户更好地了解它们之间的差异。(本文由https://www.chromegw.com/的…...

使用Python可视化支持向量机(SVM)
支持向量机(SVM)是用于分类和回归任务的强大监督学习模型。它们受欢迎背后的一个关键因素是它们有效处理线性和非线性数据的能力。在本文中,我们将探索使用Python和流行的库(如scikit-learn和Matplotlib)可视化SVM。 …...

C++泛型编程
一、什么是泛型编程 泛型编程 是一种编程范式,它通过编写可以处理多种数据类型的代码来实现代码的灵活复用。泛型编程主要通过模板来实现。 比如我们日常使用的容器类型vector就应用了模板来实现其通用性,我们在使用时可以通过传入型别创建对应的动态数…...
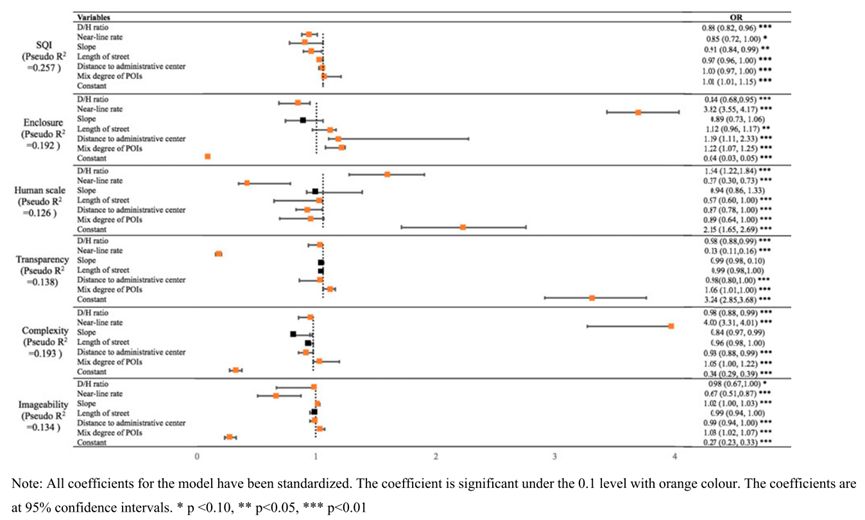
【论文分享】利用大量街景图片研究街道空间质量与建筑环境属性之间的关联
本研究通过有序逻辑回归模型,结合街景图片和街道数据,分析了街道空间质量与建筑环境属性的关系。通过Kappa分析和相关性分析,确定了影响街道空间质量的因素,并绘制了质量分布图。这些因素与街道质量的不同维度相关联,对…...

【Linux第七课--基础IO】内存级文件、重定向、缓冲区、文件系统、动态库静态库
目录 引入内存级文件重新使用C文件接口 -- 对比重定向写文件读文件文件流 认识文件操作的系统接口open参数 -- flagflag的内容宏的传参方式 open关闭文件写文件读文件结论 引入文件描述符fd、对文件的理解理解一切皆文件方法集文件fd的分配规则 重定向代码的重定向输入重定向输…...

对比C/C++语言,Rust语言有什么优势?
Rust语言相较于C/C语言有以下几个主要优势: 1. 内存安全:Rust通过其所有权系统和借用规则在编译时捕获许多常见的内存安全错误,如空指针引用和数据竞争,避免了许多常见的安全漏洞。这与C/C不同,后者通常需要手动管理内…...

Rust语言有哪些数据类型?
Rust语言的数据类型主要包括以下几种: 一、基本数据类型 1. 整数类型 i8, i16, i32, i64, i128: 有符号整数 u8, u16, u32, u64, u128: 无符号整数 isize, usize: 根据平台选择大小的整数(通常用于指针和索引) 2. 浮点数类型 f32: 32位浮…...

【论文笔记】Attention Prompting on Image for Large Vision-Language Models
🍎个人主页:小嗷犬的个人主页 🍊个人网站:小嗷犬的技术小站 🥭个人信条:为天地立心,为生民立命,为往圣继绝学,为万世开太平。 基本信息 标题: Attention Prompting on I…...

VScode设置系统界面字体
现象: 系统界面字体太大,导致菜单栏字体显示不全,每次使用都要先点然后才能打开终端和帮助 缩小字体应该就可以实现全部都看到的效果 步骤 Window: Zoom Level 调整所有窗口的默认缩放级别。大于“0”的每个增量(例如“1”&…...

Java中常见的异常类型
1、Exception和Error有什么区别? 首先Exception和Error都是继承于Throwable类,在Java中只有Throwable类型的实例才可以被抛出(throw)或者捕获(catch),它是异常处理机制的基本组成类型。 Except…...
)
Java学习Day58:相声二人组!(项目统计数据Excel图表导出)
<!DOCTYPE html> <html xmlns"http://www.w3.org/1999/html"><head><!-- 页面meta --><meta charset"utf-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><title>瑞通健康</tit…...

springboot 自动装配和bean注入原理及实现
装配:创建bean,并加入IOC容器。 注入:创建bean之间的依赖关系。 1、类自动装配 SpringBoot 自动装配使得开发人员可以轻松地搭建、配置和运行应用程序,而无需手动管理大部分的 bean 和配置。 Spring Boot 的自动装配机制与模块…...
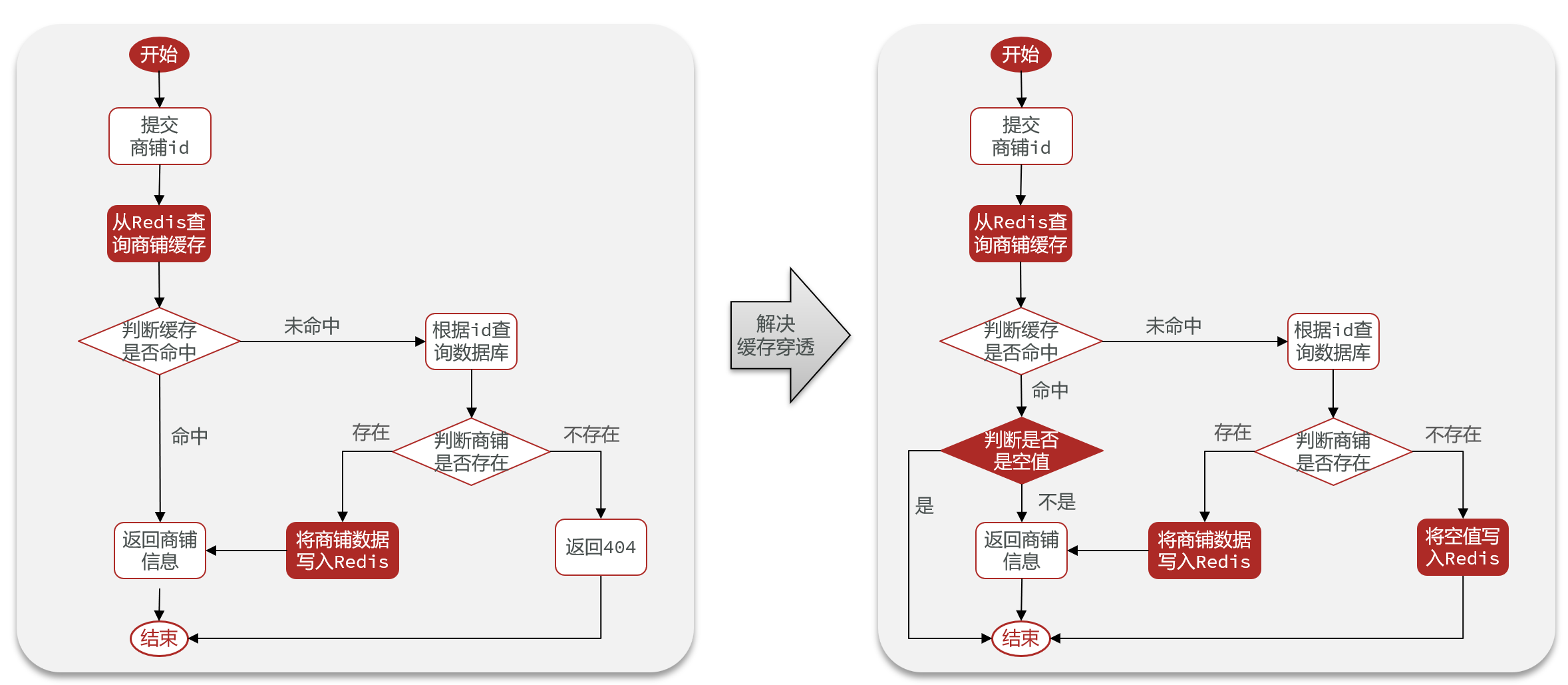
解决Redis缓存穿透(缓存空对象、布隆过滤器)
文章目录 背景代码实现前置实体类常量类工具类结果返回类控制层 缓存空对象布隆过滤器结合两种方法 背景 缓存穿透是指客户端请求的数据在缓存中和数据库中都不存在,这样缓存永远不会生效,这些请求都会打到数据库 常见的解决方案有两种,分别…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

Visual Studio Code 扩展
Visual Studio Code 扩展 change-case 大小写转换EmmyLua for VSCode 调试插件Bookmarks 书签 change-case 大小写转换 https://marketplace.visualstudio.com/items?itemNamewmaurer.change-case 选中单词后,命令 changeCase.commands 可预览转换效果 EmmyLua…...

C++_哈希表
本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说,直接开始吧! 一、基础概念 1. 哈希核心思想: 哈希函数的作用:通过此函数建立一个Key与存储位置之间的映射关系。理想目标:实现…...

土建施工员考试:建筑施工技术重点知识有哪些?
《管理实务》是土建施工员考试中侧重实操应用与管理能力的科目,核心考查施工组织、质量安全、进度成本等现场管理要点。以下是结合考试大纲与高频考点整理的重点内容,附学习方向和应试技巧: 一、施工组织与进度管理 核心目标: 规…...

鸿蒙HarmonyOS 5军旗小游戏实现指南
1. 项目概述 本军旗小游戏基于鸿蒙HarmonyOS 5开发,采用DevEco Studio实现,包含完整的游戏逻辑和UI界面。 2. 项目结构 /src/main/java/com/example/militarychess/├── MainAbilitySlice.java // 主界面├── GameView.java // 游戏核…...

aardio 自动识别验证码输入
技术尝试 上周在发学习日志时有网友提议“在网页上识别验证码”,于是尝试整合图像识别与网页自动化技术,完成了这套模拟登录流程。核心思路是:截图验证码→OCR识别→自动填充表单→提交并验证结果。 代码在这里 import soImage; import we…...

C++--string的模拟实现
一,引言 string的模拟实现是只对string对象中给的主要功能经行模拟实现,其目的是加强对string的底层了解,以便于在以后的学习或者工作中更加熟练的使用string。本文中的代码仅供参考并不唯一。 二,默认成员函数 string主要有三个成员变量,…...
