数据结构 —— 红黑树
目录
1. 初识红黑树
1.1 红黑树的概念
1.2 红⿊树的规则
1.3 红黑树如何确保最长路径不超过最短路径的2倍
1.4 红黑树的效率:O(logN)
2. 红黑树的实现
2.1 红黑树的基础结构框架
2.2 红黑树的插⼊
2.2.1 情况1:变色
2.2.2 情况2:单旋+变色
2.2.3 情况3:双旋+变色
2.3 验证一棵树是否为红黑树
2.4 代码汇总
1. 初识红黑树
1.1 红黑树的概念
红⿊树是⼀棵⼆叉搜索树,他的每个结点增加⼀个存储位来表⽰结点的颜⾊,可以是红⾊或者⿊⾊。通过对任何⼀条从根到叶⼦的路径上各个结点的颜⾊进⾏约束,红⿊树确保没有⼀条路径会⽐其他路径⻓出2倍,因⽽是接近平衡的
1.2 红⿊树的规则
1. 每个结点不是红⾊就是⿊⾊
2. 根结点是⿊⾊的
3. 如果⼀个结点是红⾊的,则它的两个孩⼦结点必须是⿊⾊的,也就是说任意⼀条路径不会有连续的红⾊结点
4. 对于任意⼀个结点,从该结点到其所有NULL结点的简单路径上,均包含相同数量的⿊⾊结点



1.3 红黑树如何确保最长路径不超过最短路径的2倍
1. 由规则4可知,从根到NULL结点的每条路径都有相同数量的⿊⾊结点,所以极端场景下,最短路径就就是全是⿊⾊结点的路径,假设最短路径⻓度为bh(黑色节点的数量)
2. 由规则2和规则3可知,任意⼀条路径不会有连续的红⾊结点,所以极端场景下,最⻓的路径就是⼀⿊⼀红间隔组成,那么最⻓路径的⻓度为2*bh
3. 综合红⿊树的4点规则⽽⾔,理论上的全⿊最短路径和⼀⿊⼀红的最⻓路径并不是在每棵红⿊树都存在的。假设任意⼀条从根到NULL结点路径的⻓度为x,那么bh <= h <= 2*bh
1.4 红黑树的效率:O(logN)
红⿊树的表达相对AVL树要抽象⼀些,AVL树通过⾼度差直观的控制了平衡。红⿊树通过4条规则的颜 ⾊约束,间接的实现了近似平衡,他们效率都是同⼀档次,但是相对⽽⾔,插⼊相同数量的结点,红⿊树的旋转次数是更少的,因为他对平衡的控制没那么严格

2. 红黑树的实现

2.1 红黑树的基础结构框架
#pragma once
//定义一个枚举
enum Colour
{//枚举里面定义颜色RED,BLACK
};//默认按key/value结构实现
template<class K, class V>
struct RBTreeNode
{//这⾥更新控制平衡也要加⼊parent指针pair<K, V> _kv;//也要实现成三叉链RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;Colour _col;RBTreeNode(const pair<K, V>& kv) :_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr){}
};template<class K, class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
public:
private:Node* _root = nullptr;
};2.2 红黑树的插⼊
1. 插⼊⼀个值按⼆叉搜索树规则进⾏插⼊,插⼊后我们只需要观察是否符合红⿊树的4条规则
2. 如果是空树插⼊,新增结点是⿊⾊结点。如果是⾮空树插⼊,新增结点必须是红⾊结点,因为⾮空树插⼊,新增⿊⾊结点就破坏了规则4,规则4是很难维护的
3. ⾮空树插⼊后,新增结点必须红⾊结点,如果⽗亲结点是⿊⾊的,则没有违反任何规则,插⼊结束
4. ⾮空树插⼊后,新增结点必须红⾊结点,如果⽗亲结点是红⾊的,则违反规则3。进⼀步分析,c是红⾊,p为红,g必为⿊,这三个颜⾊都固定了,关键的变化看u的情况,需要根据u分为以下⼏种 情况分别处理
说明:下图中假设我们把新增结点标识为c(cur),c的⽗亲标识为p(parent),p的⽗亲标识为 g(grandfather),p的兄弟标识为u(uncle)

2.2.1 情况1:变色
新增结点标识为c(cur),c的⽗亲标识为p(parent),p的⽗亲标识为 g(grandfather),p的兄弟标识为u(uncle)
c为红,p为红,g为⿊,u存在且为红,则将p和u变⿊,g变红,再在把g当做新的c,继续往上更新
分析:因为p和u都是红⾊,g是⿊⾊,把p和u变⿊,左边⼦树路径各增加⼀个⿊⾊结点,g再变红,相当于保持g所在⼦树的⿊⾊结点的数量不变,同时解决了c和p连续红⾊结点的问题,需要继续往上更新因为,g是红⾊
如果g的⽗亲还是红⾊,那么就还需要继续处理;如果g的⽗亲是⿊⾊,则处理结束了;如果g就是整棵树的根,再把g变回⿊⾊
情况1只变⾊,不旋转。所以⽆论c是p的左还是右,p是g的左还是右,都是上⾯的变⾊处理⽅式

2.2.2 情况2:单旋+变色
c为红,p为红,g为⿊,u不存在或者u存在且为⿊,u不存在,则c⼀定是新增结点
u存在且为⿊,则c⼀定不是新增,c之前是⿊⾊的,是在c的⼦树中插⼊,符合情况1,变⾊将c从⿊⾊变成红⾊,更新上来的
分析:p必须变⿊,才能解决,连续红⾊结点的问题,u不存在或者是⿊⾊的,这⾥单纯的变⾊⽆法解决问题,需要旋转+变⾊

如果p是g的左,c是p的左,那么以g为旋转点进⾏右单旋,再把p变⿊,g变红即可。p变成课这颗树新的根,这样⼦树⿊⾊结点的数量不变,没有连续的红⾊结点了,且不需要往上更新,因为p的⽗亲是⿊⾊还是红⾊或者空都不违反规则

如果p是g的右,c是p的右,那么以g为旋转点进⾏左单旋,再把p变⿊,g变红即可。p变成课这颗树新的根,这样⼦树⿊⾊结点的数量不变,没有连续的红⾊结点了,且不需要往上更新,因为p的⽗亲是⿊⾊还是红⾊或者空都不违反规则
2.2.3 情况3:双旋+变色
c为红,p为红,g为⿊,u不存在或者u存在且为⿊,u不存在,则c⼀定是新增结点
u存在且为⿊,则c⼀定不是新增,c之前是⿊⾊的,是在c的⼦树中插⼊,符合情况1,变⾊将c从⿊⾊变成红⾊,更新上来的
分析:p必须变⿊,才能解决,连续红⾊结点的问题,u不存在或者是⿊⾊的,这⾥单纯的变⾊⽆法解决问题,需要旋转+变⾊

如果p是g的左,c是p的右,那么先以p为旋转点进⾏左单旋,再以g为旋转点进⾏右单旋,再把c变⿊,g变红即可。c变成课这颗树新的根,这样⼦树⿊⾊结点的数量不变,没有连续的红⾊结点了,且不需要往上更新,因为c的⽗亲是⿊⾊还是红⾊或者空都不违反规则

如果p是g的右,c是p的左,那么先以p为旋转点进⾏右单旋,再以g为旋转点进⾏左单旋,再把c变⿊,g变红即可。c变成课这颗树新的根,这样⼦树⿊⾊结点的数量不变,没有连续的红⾊结点了,且不需要往上更新,因为c的⽗亲是⿊⾊还是红⾊或者空都不违反规则
2.3 验证一棵树是否为红黑树
规则1:枚举颜⾊类型,天然实现保证了颜⾊不是⿊⾊就是红⾊
规则2:直接检查根即可
规则3:前序遍历检查,遇到红⾊结点查孩⼦不太⽅便,因为孩⼦有两个,且不⼀定存在,反过来检 查⽗亲的颜⾊就⽅便多了
规则4:前序遍历,遍历过程中⽤形参记录跟到当前结点的blackNum(⿊⾊结点数量),前序遍历遇到 ⿊⾊结点就++blackNum,⾛到空就计算出了⼀条路径的⿊⾊结点数量。再任意⼀条路径⿊⾊结点数量作为参考值,依次⽐较即可
bool Check(Node* root, int blacknum, const int retnum)
{if (root == nullptr){if (blacknum != retnum){cout << "有路径的黑色节点个数与其他路径不相同" << endl;return false;}return true;}if (root->_col == RED && root->_parent->_col == RED){cout << "存在连续的红色节点" << endl;return false;}if (root->_col == BLACK){blacknum++;}return Check(root->_left, blacknum, retnum)&& Check(root->_right, blacknum, retnum);
}
bool IsBalance()
{if (_root == nullptr){return true;}if (_root->_col == BLACK){return false;}int retnum = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK){retnum++;}cur = cur->_left;}return Check(_root, 0, retnum);
}2.4 代码汇总
#pragma once
#pragma once
//定义一个枚举
enum Colour
{//枚举里面定义颜色RED,BLACK
};//默认按key/value结构实现
template<class K, class V>
struct RBTreeNode
{//这⾥更新控制平衡也要加⼊parent指针pair<K, V> _kv;//也要实现成三叉链RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;Colour _col;//颜色RBTreeNode(const pair<K, V>& kv) :_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr){}
};template<class K, class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
public://按二叉搜索树规则进行插入bool Insert(const pair<K, V>& kv){//如果是空树插入第一个节点if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;//根节点为黑色return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}//如果非空的树插入一个节点,那么插入红色cur = new Node(kv);cur->_col = RED;if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}// 链接父亲cur->_parent = parent;// 父亲存在并且也是红色,当出现连续的红色节点时while (parent && parent->_col == RED){//找到爷爷节点Node* grandfather = parent->_parent;//再根据叔叔节点来判断父亲节点的情况if (parent == grandfather->_left){// g//p u// //说明u在g的右边Node* uncle = grandfather->_right;//如果u存在并且u的颜色为红色if (uncle && uncle->_col == RED){//将u和p的颜色改为黑色,g的颜色改为红色uncle->_col = parent->_col = BLACK;grandfather->_col = RED;// 继续往上处理cur = grandfather;parent = cur->_parent;//p寻找g的p节点}else{if (cur == parent->_left){// g// p u// cRotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// g// p u// cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else{// g// u pNode* uncle = grandfather->_left;// 叔叔存在且为红,-》变色即可if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 继续往上处理cur = grandfather;parent = cur->_parent;}else // 叔叔不存在,或者存在且为黑{// 情况二:叔叔不存在或者存在且为黑// 旋转+变色// g// u p// cif (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}//保证根节点一定是黑色的_root->_col = BLACK;return true;}//右单旋void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* pParent = parent->_parent;subL->_right = parent;parent->_parent = subL;if (parent == _root){_root = subL;subL->_parent = nullptr;}else{if (pParent->_left == parent){pParent->_left = subL;}else{pParent->_right = subL;}subL->_parent = pParent;}}//左单旋void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;Node* parentParent = parent->_parent;subR->_left = parent;parent->_parent = subR;if (parentParent == nullptr){_root = subR;subR->_parent = nullptr;}else{if (parent == parentParent->_left){parentParent->_left = subR;}else{parentParent->_right = subR;}subR->_parent = parentParent;}}private:Node* _root = nullptr;
};完结撒花~
相关文章:

数据结构 —— 红黑树
目录 1. 初识红黑树 1.1 红黑树的概念 1.2 红⿊树的规则 1.3 红黑树如何确保最长路径不超过最短路径的2倍 1.4 红黑树的效率:O(logN) 2. 红黑树的实现 2.1 红黑树的基础结构框架 2.2 红黑树的插⼊ 2.2.1 情况1:变色 2.2.2 情况2:单旋变色 2.2…...

《功能高分子学报》
《功能高分子学报》 中国标准连续出版物号:CN 31-1633/O6,国际标准连续出版物号:ISSN 1008-9357,邮发代号:4-629,刊期:双月刊。 《功能高分子学报》主要刊登功能高分子和其他高分子领域具有创新意义的学术…...

Linux特种文件系统--tmpfs文件系统
tmpfs类似于RamDisk(只能使用物理内存),使用虚拟内存(简称VM)子系统的页面存储文件。tmpfs完全依赖VM,遵循子系统的整体调度策略。说白了tmpfs跟普通进程差不多,使用的都是某种形式的虚拟内存&a…...

《基于STMF103的FreeRTOS内核移植》
目录 1.FreeRTOS资料下载与出处 1.1官网下载,网址:www.freertos.org 1.2在正点原子官网,任意STM32F1的开发板资料A盘里, 2.FreeRTOS移植重要文件讲解 2.1 FreeRTOS与FreeRTOS-Plus文件夹 2.2 Demo、Lincence、Source ●Demo文件…...

一七二、Vue3性能优化方式
Vue 3 的性能优化相较于 Vue 2 有了显著提升,利用新特性和改进方法可以更高效地构建和优化应用。以下是 Vue 3 的常见性能优化方法及示例。 1. 使用组合式 API (Composition API) Vue 3 引入的组合式 API,通过逻辑拆分和复用来实现更高效的代码组织和性…...

软件测试--BUG篇
博主主页: 码农派大星. 数据结构专栏:Java数据结构 数据库专栏:MySQL数据库 JavaEE专栏:JavaEE 软件测试专栏:软件测试 关注博主带你了解更多知识 目录 1. 软件测试的⽣命周期 2. BUG 1. BUG 的概念 2. 描述bug的要素 3.bug级别 4.bug的⽣命周期 5 与开发产⽣争执怎…...

Scikit-learn和Keras简介
一,Scikit-learn是一个开源的机器学习库,用于Python编程语言。它建立在NumPy、SciPy和matplotlib这些科学计算库之上,提供了简单有效的数据挖掘和数据分析工具。Scikit-learn库包含了许多用于分类、回归、聚类和降维的算法,包括支…...

python在word的页脚插入页码
1、插入简易页码 import win32com.client as win32 from win32com.client import constants import osdoc_app win32.gencache.EnsureDispatch(Word.Application)#打开word应用程序 doc_app.Visible Truedoc doc_app.Documents.Add() footer doc.Sections(1).Footers(cons…...

Java面试题十四
一、Java中的JNI(Java Native Interface)是什么?它有什么用途? Java中的JNI(Java Native Interface)是Java提供的一种编程框架,它允许Java代码与本地(Native)代码&#x…...

yarn : 无法加载文件,未对文件 进行数字签名。无法在当前系统上运行该脚本。
执行这个命令时报错:yarn --registryhttps://registry.npm.taobao.org yarn : 无法加载文件 C:\Users\Administrator\AppData\Roaming\npm\yarn.ps1。未对文件 C:\Users\Administ rator\AppData\Roaming\npm\yarn.ps1 进行数字签名。无法在当前系统上运行该脚本。有…...

Hadoop——HDFS
什么是HDFS HDFS(Hadoop Distributed File System)是Apache Hadoop的核心组件之一,是一个分布式文件系统,专门设计用于在大规模集群上存储和管理海量数据。它的设计目标是提供高吞吐量的数据访问和容错能力,以支持大数…...

计算机的一些基础知识
文章目录 编程语言 程序 所谓程序,就是 一组指令 以及 这组指令要处理的数据。狭义上来说,程序对我们来说,通常表现为一组文件。 程序 指令 指令要处理的数据。 编程语言发展 机器语言:0、1 二进制构成汇编语言:…...

学习RocketMQ(记录了个人艰难学习RocketMQ的笔记)
一、部署单点RocketMQ Docker 部署 RocketMQ (图文并茂超详细)_docker 部署rocketmq-CSDN博客 这个博主讲的很好,可食用,替大家实践了一遍 二、原理篇 为什么使用RocketMQ: 为什么选择RocketMQ | RocketMQ 关于一些原理,感觉…...

【设计模式】策略模式定义及其实现代码示例
文章目录 一、策略模式1.1 策略模式的定义1.2 策略模式的参与者1.3 策略模式的优点1.4 策略模式的缺点1.5 策略模式的使用场景 二、策略模式简单实现2.1 案例描述2.2 实现代码 三、策略模式的代码优化3.1 优化思路3.2 抽象策略接口3.3 上下文3.4 具体策略实现类3.5 测试 参考资…...
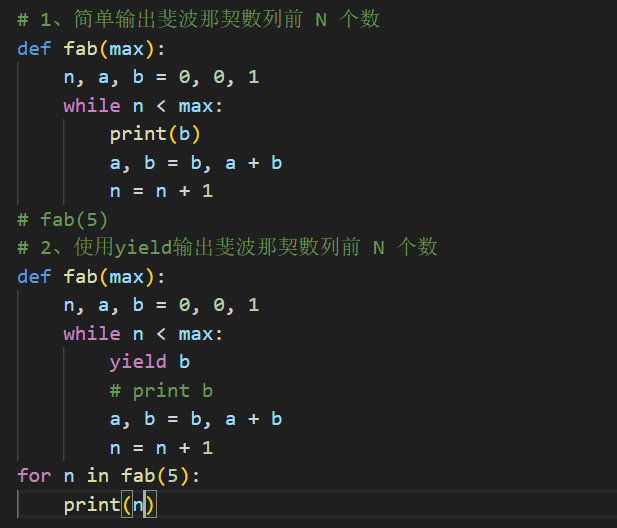
list与iterator的之间的区别,如何用斐波那契数列探索yield
问题 list与iterator的之间的区别是什么?如何用斐波那契数列探索yield? 2 方法 将数据转换成list,通过对list索引和切片操作,以及可以进行添加、删除和修改元素。 iterator是一种对象,用于遍历可迭代对象(如列表、元组…...

抖音店铺数据也就是抖店,如何使用小店数据集来挖掘价值?
抖音商家现在基本达到二百多万家抖店,有一些公司可能会根据开放的数据研究行业分布、GMV等等,就像是也出了专业的一些平台如“蝉妈妈”、“达多多”,对我来说受限制就是难受。 当然也有很多大型合法的数据平台有抖店数据集,但…...

KubeVirt 安装和配置 Windows虚拟机
本文将将介绍如何安装 KubeVirt 和使用 KubeVirt 配置 Windows 虚拟机。 前置条件 准备 Ubuntu 操作系统,一定要安装图形化界面。 安装 Docker(最新版本) 安装 libvirt 和 TigerVNC: apt install libvirt-daemon-system libvir…...

CM API方式设置YARN队列资源
简述 对于CDH版本我们可以参考Fayson的文章,本次是CDP7.1.7 CM7.4.4 ,下面只演示一个设置队列容量百分比的示例,其他请参考cloudera官网。 获取cookies文件 生成cookies.txt文件 curl -i -k -v -c cookies.txt -u admin:admin http://192.168.242.100:7180/api/v44/clusters …...

Mysql常用语法一篇文章速成
文章目录 前言前置环境数据库的增删改查查询数据查询所有条件查询多条件查询模糊查询分页查询排序查询分组查询⭐️⭐️关联查询关联分页查询 添加数据insert插入多条记录不指定列名(适用于所有列都有值的情况) 更新数据更新多条记录更新多个列更新不满足条件的记录 删除统计数…...
)
Intel nuc x15 重装系统步骤和注意事项(LAPKC71F、LAPKC71E、LAPKC51E)
注意本教程的对象是11代CPU,英伟达独显的nuc x15,不是12代arc显卡的。 x15安装win11 24h2,如果在装系统时联网,windows自动下载的最新驱动有兼容问题,会导致【英特尔显卡控制中心】装不上,或者【英特尔nuc…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...


