LeetCode 684.冗余连接:拓扑排序+哈希表(O(n)) 或 并查集(O(nlog n)-O(nα(n)))
【LetMeFly】684.冗余连接:拓扑排序+哈希表(O(n)) 或 并查集(O(nlog n)-O(nα(n)))
力扣题目链接:https://leetcode.cn/problems/redundant-connection/
树可以看成是一个连通且 无环 的 无向 图。
给定往一棵 n 个节点 (节点值 1~n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间,且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ,edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。
请找出一条可以删去的边,删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案,则返回数组 edges 中最后出现的那个。
示例 1:

输入: edges = [[1,2], [1,3], [2,3]] 输出: [2,3]
示例 2:
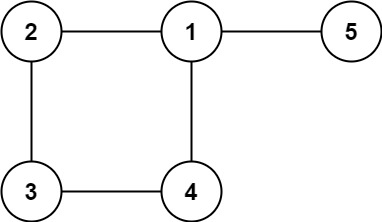
输入: edges = [[1,2], [2,3], [3,4], [1,4], [1,5]] 输出: [1,4]
提示:
n == edges.length3 <= n <= 1000edges[i].length == 21 <= ai < bi <= edges.lengthai != biedges中无重复元素- 给定的图是连通的
方法一:拓扑排序(哈希表)
记录每个点的度,使用拓扑排序的思想,每次将度为1的节点所连的边移除。
最后剩下的点就是“环”中的点,将这些点放入哈希表中。
倒叙遍历“边”,第一条两个节点都出现在哈希表中的边即为所求。
- 时间复杂度 O ( n ) O(n) O(n)
- 空间复杂度 O ( n ) O(n) O(n)
AC代码
C++
class Solution {
public:vector<int> findRedundantConnection(vector<vector<int>>& edges) {vector<int> degree(edges.size() + 1);vector<vector<int>> graph(edges.size() + 1);for (vector<int>& edge : edges) {degree[edge[0]]++;degree[edge[1]]++;graph[edge[0]].push_back(edge[1]);graph[edge[1]].push_back(edge[0]);}queue<int> q;for (int i = 1; i <= edges.size(); i++) {if (degree[i] == 1) {q.push(i);}}while (q.size()) {int thisNode = q.front();q.pop();for (int nextNode : graph[thisNode]) {degree[nextNode]--;if (degree[nextNode] == 1) {q.push(nextNode);}}}unordered_set<int> reservedNodes;for (int i = 1; i <= edges.size(); i++) {if (degree[i] > 1) {reservedNodes.insert(i);}}// for (vector<vector<int>>::iterator it = edges.rbegin(); it != edges.rend(); it++)for (int i = edges.size() - 1; i >= 0; i--) {if (reservedNodes.count(edges[i][0]) && reservedNodes.count(edges[i][1])) {return edges[i];}}return {}; // FAKE RETURN}
};
方法二:并查集
使用并查集将每条边的两个顶点加入同一个集合中,第一条两个顶点已经在一个集合中的边即为所求(加上这条边后就形成了环)。
- 时间复杂度 O ( n log n ) O(n\log n) O(nlogn),平均为 O ( n α ( n ) ) O(n\alpha(n)) O(nα(n))(接近 O ( n ) O(n) O(n))
- 空间复杂度 O ( n ) O(n) O(n)
AC代码
C++
class Solution {
private:vector<int> fa;int find(int x) {if (fa[x] != x) {fa[x] = find(fa[x]);}return fa[x];}void union_(int x, int y) {fa[find(x)] = find(y);}
public:vector<int> findRedundantConnection(vector<vector<int>>& edges) {fa.resize(edges.size() + 1);for (int i = 1; i <= edges.size(); i++) {fa[i] = i;}// for (vector<int>& edge : edges) {// union_(edge[0], edge[1]);// }// for (int i = edges.size() - 1; i > 0; i--) {// if (find(edges[i][0]) == find(edges[i][1])) {// return edges[i];// }// }for (vector<int>& edge : edges) {if (find(edge[0]) == find(edge[1])) {return edge;} else {union_(edge[0], edge[1]);}}return {}; // FAKE RETURN}
};
Python
from typing import Listclass Solution:def union(self, x: int, y: int) -> None:self.fa[self.find(x)] = self.find(y)def find(self, x: int) -> int:if self.fa[x] != x:self.fa[x] = self.find(self.fa[x])return self.fa[x]def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:self.fa = [i for i in range(len(edges) + 1)]for x, y in edges:if self.find(x) == self.find(y):return [x, y]else:self.union(x, y)return [] # FAKE RETURNJava
class Solution {private int[] fa;private int find(int x) {if (fa[x] != x) {fa[x] = find(fa[x]);}return fa[x];}private void union(int x, int y) {fa[find(x)] = find(y);}public int[] findRedundantConnection(int[][] edges) {fa = new int[edges.length + 1];for (int i = 1; i <= edges.length; i++) {fa[i] = i;}for (int[] edge : edges) {if (find(edge[0]) == find(edge[1])) {return edge;} else {union(edge[0], edge[1]);}}return new int[0];}
}
Go
package mainfunc find(fa []int, x int) int {if fa[x] != x {fa[x] = find(fa, fa[x])}return fa[x]
}func union(fa []int, x int, y int) {fa[find(fa, x)] = find(fa, y)
}func findRedundantConnection(edges [][]int) []int {fa := make([]int, len(edges) + 1)for th, _ := range fa {fa[th] = th}for _, edge := range edges {if find(fa, edge[0]) == find(fa, edge[1]) {return edge} else {union(fa, edge[0], edge[1])}}return nil
}
同步发文于CSDN和我的个人博客,原创不易,转载经作者同意后请附上原文链接哦~
Tisfy:https://letmefly.blog.csdn.net/article/details/143464726
今晚(20241102晚10:30)这会儿api.github.com似乎出了点问题,国内外都访问不到X_X
相关文章:

LeetCode 684.冗余连接:拓扑排序+哈希表(O(n)) 或 并查集(O(nlog n)-O(nα(n)))
【LetMeFly】684.冗余连接:拓扑排序哈希表(O(n)) 或 并查集(O(nlog n)-O(nα(n))) 力扣题目链接:https://leetcode.cn/problems/redundant-connection/ 树可以看成是一个连通且 无环 的 无向 图。 给定往…...

让空气净化器“很听话”-置入NRK3502离线语音控制芯片
一、产品市场 随着智能家居的快速发展,人们对家居环境的舒适度与健康性要求日益提升,空气净化器作为改善室内空气质量的重要设备,其智能化升级变得尤为关键。让空气净化器“很听话”,不再仅仅是一个遥不可及的设想,而…...
8个Visio最佳替代软件推荐,每一款都堪称绘图神器
上午好,我的网工朋友。 绘图软件Visio是微软旗下知名的绘图软件,可用来绘制各种可视化图形,包括但不限于:流程图、人物关系图、组织架构图、思维导图、UML图、泳道图、甘特图、知识地图、软件架构图、鱼骨图等 它支持绘制的图形…...
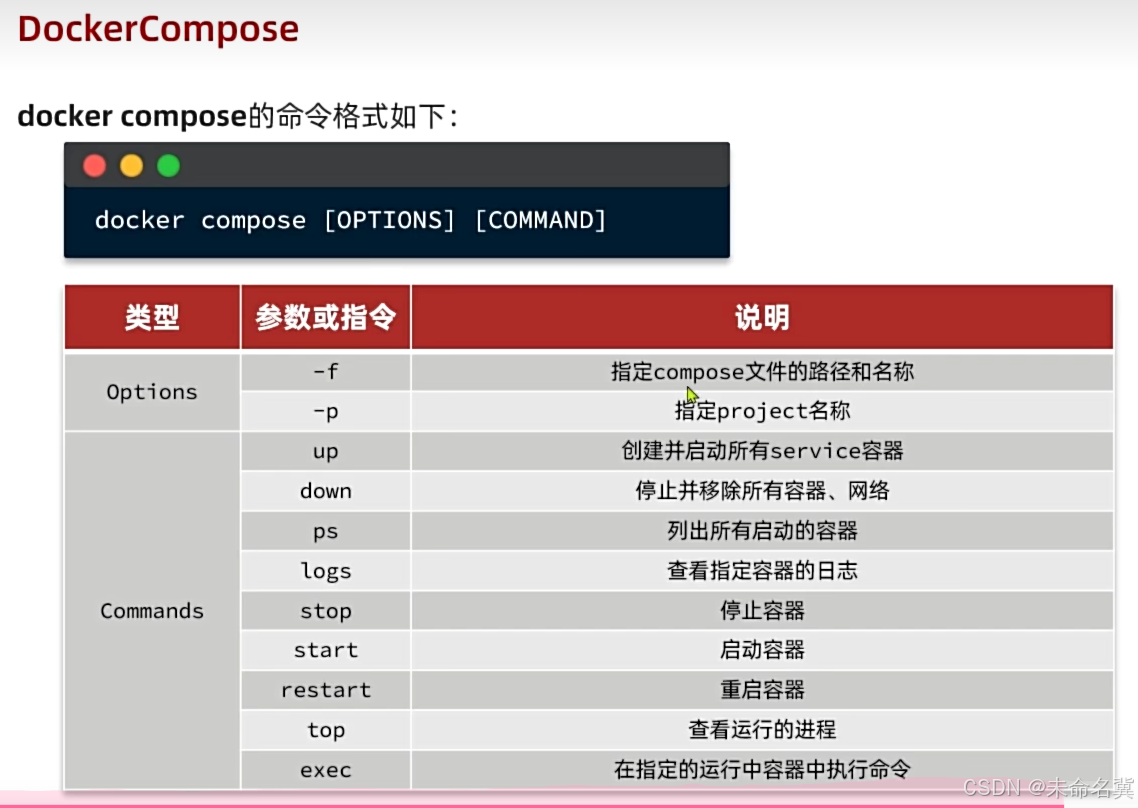
微服务day02
教学文档: 黑马教学文档 Docker Docker的安装 镜像和容器 命令解读 常见命令 案例 查看DockerHub,拉取Nginx镜像,创建并运行容器 搜索Nginx镜像:在 www.hub.docker.com 网站进行查询 拉取镜像: docker pull ngin…...

使用 Logback 的最佳实践:`logback.xml` 与 `logback-spring.xml` 的区别与用法
在开发 Spring Boot 项目时,日志是调试和监控的重要工具。Spring Boot 默认支持 Logback 作为日志系统,并提供了 logback.xml 和 logback-spring.xml 两种配置方式。这篇文章将详细介绍这两者的区别、各自的优缺点以及最佳实践。 目录 一、什么是 Logbac…...

NSET or MSET算法--原理解析
1.背景 NSET/MSET是一种非线性的多元预测诊断技术,广泛应用于系统状态估计、故障诊断和预测等领域;相比于传统的线性模型和方法,NSET/MSET能够更好地处理非线性系统,并提供更准确的预测和诊断能力。在早期,MSET融合了…...
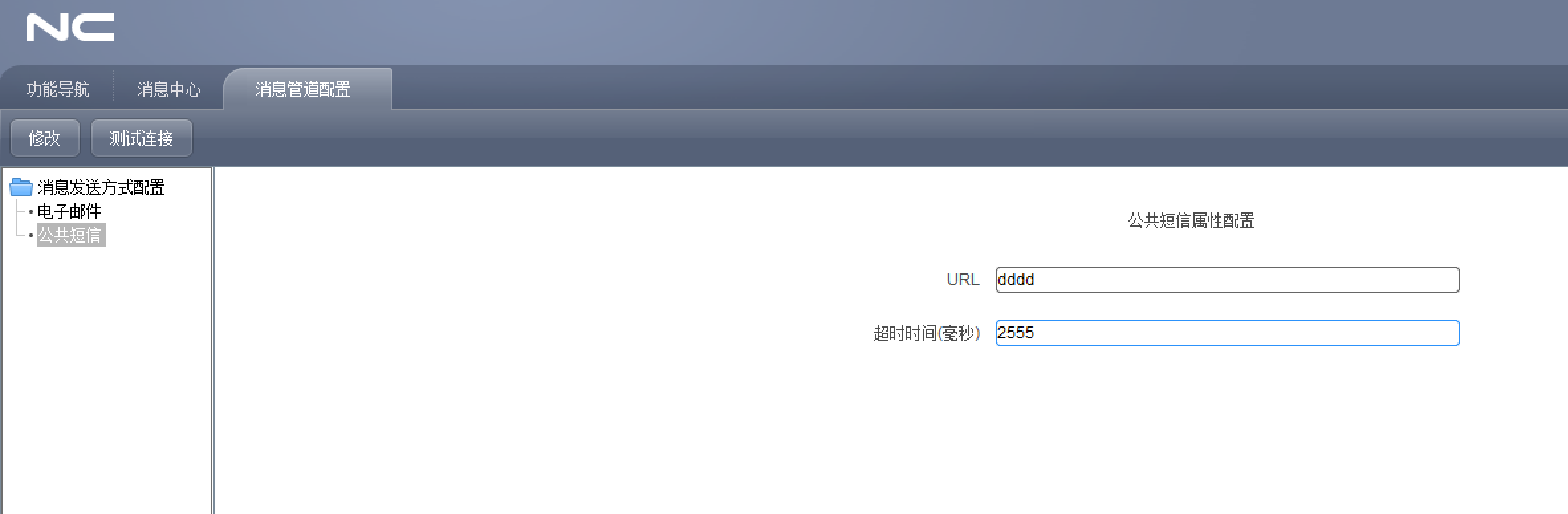
NC6 系统配置的消息渠道配置配置涉及相关的表,用户使用admin登录
NC6 系统配置的消息渠道配置配置涉及相关的表 --电子邮件、公共短信属性值配置表,比如邮箱类型、邮件发送服务器、用户、密码、发件人地址、url等。 SELECT * FROM sm_msg_stypeprop;--消息发送方式配置:电子邮件,公共短信。 SELECT * FROM sm_msg_stypebase WHERE active …...

PXC数据库性能测试对比
mysql单机 #初始化测试数据 sysbench /usr/share/sysbench/oltp_read_write.lua --mysql-host=xxx.xxx.xxx.xxx --mysql-db=test --mysql-user=hzhadmin --mysql-password=Admi --tables=10 --table-size=1000000 prepare#运行性能测试 sysbench /usr/share/sysbench/oltp_rea…...

使用AutoMySQLBackup 数据库自动备份
1.下载地址 AutoMySQLBackup的下在地址为http://sourceforge.net/projects/automysqlbackup/ 。 目前最新版本为automysqlbackup-v3.0_rc6.tar.gz 2.解压缩 把下载的automysqlbackup-v3.0_rc6.tar.gz文件拷贝到/usr/tmp下面 在/usr/local下面新建一个automysqlbackup文件夹…...

NVR批量管理软件/平台EasyNVR多个NVR同时管理支持对接阿里云、腾讯云、天翼云、亚马逊S3云存储
随着云计算技术的日益成熟,越来越多的企业开始将其业务迁移到云端,以享受更为灵活、高效且经济的服务模式。在视频监控领域,云存储因其强大的数据处理能力和弹性扩展性,成为视频数据存储的理想选择。NVR批量管理软件/平台EasyNVR&…...

13.React useTimeout
在 React 应用中,延迟执行某些操作是一个常见需求。传统的 setTimeout 在函数组件中使用可能会导致一些问题,如闭包陷阱或难以正确清理。useTimeout 钩子提供了一种声明式的方法来实现延迟执行,使得定时器的管理更加简单和可靠。这个自定义钩子不仅简化了定时器的使用,还解…...

Android待机问题与内存泄露日志定位及bugreport获取分析
文章目录 bugreportbugreport介绍获取bugreport日志分析bugreport安卓平台log获取日志android.logkernel.logkernel.log查看待机过程sysinfo.log判断内存是否有泄露分析bugreport,定位唤醒源,判断是否有ANR。分析安卓log,定位待机唤醒功耗问题,判断是否有内存泄露。bugrepo…...
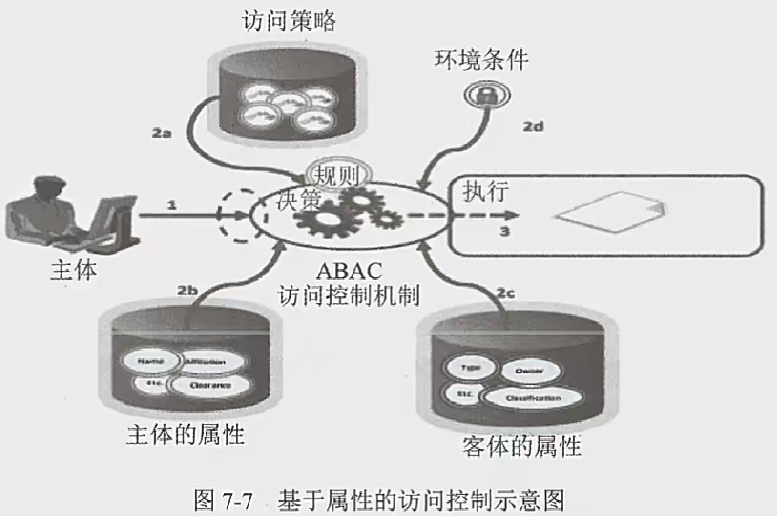
访问控制技术原理与应用
目录 访问控制概述实现访问控制目标访问控制参考模型常见访问控制模型访问控制模型-DAC自主访问控制访问控制模型-MAC强制访问控制访问控制模型-RBAC基于角色的访问控制访问控制模型-ABAC基于属性的访问控制 访问控制概述 访问控制是对资源对象的访问授权控制的方法以及运行机…...

详解Rust标准库:Vec向量
查看本地官方文档 安装rust后运行 rustup doc查看The Standard Library即可获取标准库内容 std::vec::Vec定义 Vec除了可以作为动态数组还可以模拟为一个栈,仅使用push、pop即可 Vec默认分配在堆上,对于一个容量为4,有两个元素a、b的向量…...
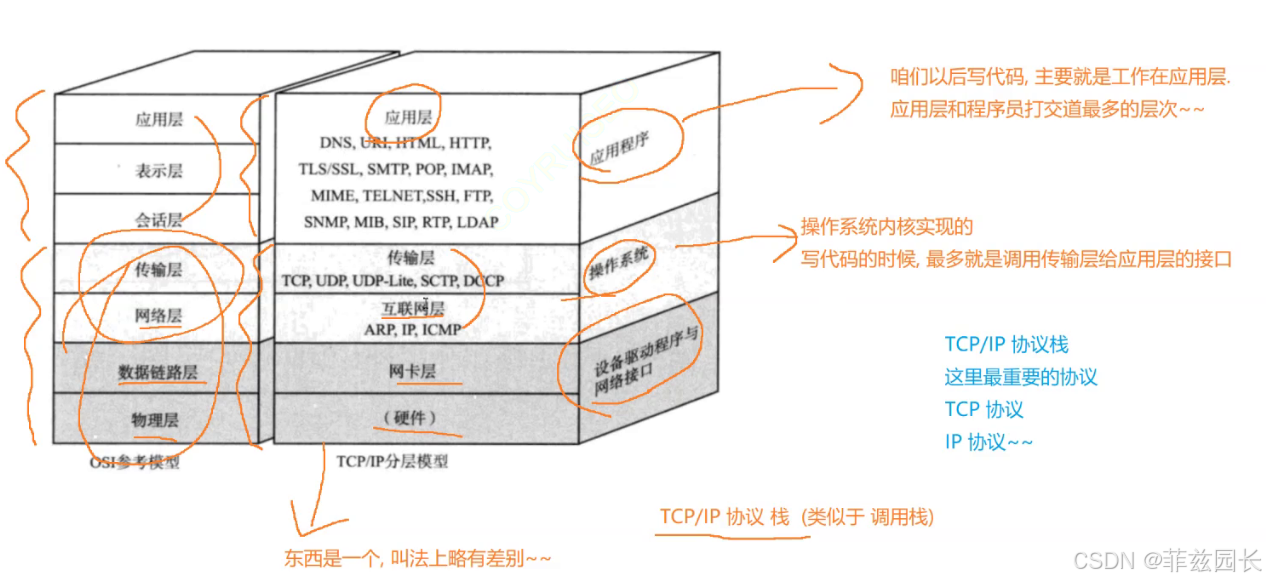
网络原理(初一,TCP/IP五层(或四层)模型面试问题)
TCP/IP五层(或四层)模型 TCP/IP是⼀组协议的代名词,它还包括许多协议,组成了TCP/IP协议簇。 TCP/IP通讯协议采⽤了5层的层级结构,每⼀层都呼叫它的下⼀层所提供的⽹络来完成⾃⼰的需求。 • 应⽤层:负责…...

Unity引擎材质球残留贴图引用的处理
大家好,我是阿赵。 这次来分享一下Unity引擎材质球残留贴图引用的处理 一、 问题 在使用Unity调整美术效果的时候,我们很经常会有这样的操作,比如: 1、 同一个材质球切换不同的Shader、 比如我现在有2个Shader,…...

Flutter鸿蒙next中封装一个列表组件
1. 创建Flutter项目 首先,确保你已经安装了Flutter SDK,并创建一个新的Flutter项目: flutter create podcast_app cd podcast_app2. 封装列表组件 我们将在lib目录下创建一个新的文件,命名为podcast_list.dart,用于…...
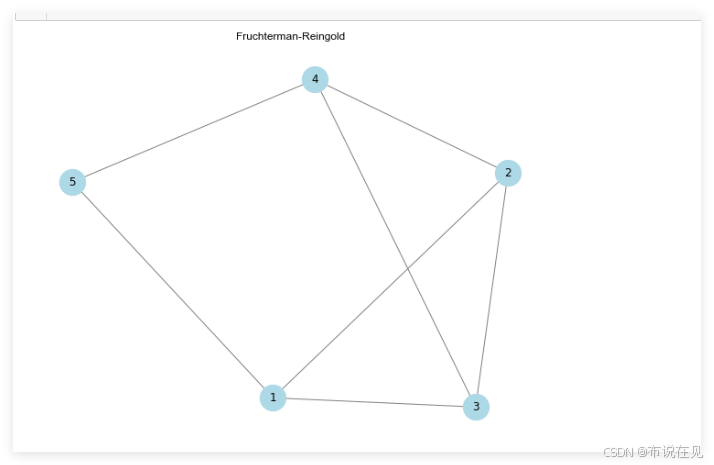
层次与网络的视觉对话:树图与力引导布局的双剑合璧
目录 目的内容树图绘制目的步骤参考代码结果与分析 力引导布局算法目的参考代码结果与分析 总结 目的 掌握常用可视化软件与工具:学习和熟练使用常用的数据可视化软件和工具,如Matplotlib、Seaborn、Plotly、Tableau等。这些工具提供了用于创建图表、图…...
python将数据集中所有文件名升序制作txt文件(医学影像)
import os import re # 设定图像文件所在的路径 img_path ./2d/images/ #需修改路径 # 获取该路径下的所有文件名 img_list os.listdir(img_path) # 过滤出以.nii结尾的文件名 nii_list [f for f in img_list if f.endswith(.nii)] # 使用正则表达式从文件名中提…...

【The Art of Unit Testing 3_自学笔记06】3.4 + 3.5 单元测试核心技能之:函数式注入与模块化注入的解决方案简介
文章目录 3.4 函数式依赖注入技术 Functional injection techniques3.5 模块化依赖注入技术 Modular injection techniques 写在前面 上一篇的最后部分对第三章后续内容做了一个概括性的梳理,并给出了断开依赖项的最简单的实现方案,函数参数值注入法。本…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...
