NSET or MSET算法--原理解析
1.背景
- NSET/MSET是一种非线性的多元预测诊断技术,广泛应用于系统状态估计、故障诊断和预测等领域;相比于传统的线性模型和方法,NSET/MSET能够更好地处理非线性系统,并提供更准确的预测和诊断能力。
- 在早期,MSET融合了模式识别技术和序贯概率比检验方法,主要应用于核电厂信号验证、仪表精度监控以及组件运行失常等监控场景的研究工作。
2.应用
- 工业监控:MSET可用于监测和预测工业设备的状态和性能。通过分析传感器数据和监测参数,MSET可以实时监测设备的运行状态,及时检测异常情况,预测设备故障,并提供预警和维修建议。
- 电力系统:MSET可以用于电力系统的状态估计和故障检测。它可以通过分析电力系统中的电流、电压、频率等参数,实时监测电力系统的运行状态,检测潜在的故障或异常情况,并提供故障诊断和恢复策略。
3.概念原理
3.1流程简介
非线性状态估计(NSET)方法是将当前运行数据和已生成的历史运行状态进行对比,计算并比较多状态变量之间的相似度,从而进行故障预警的方法。
3.2流程图

3.3逐步解析
1)观测矩阵
观测矩阵形象的表示就是一组多变量多步时间数据,其中有m个时间状态,每个时间状态有n个变量数据。
( x 11 x 12 . . . x 1 m x 21 x 22 . . . x 2 m . . . . . . . . . . . . x n 1 x n 2 . . . x n m ) \begin{equation} %开始数学环境 \left( %左括号 \begin{array}{ccc} %该矩阵一共3列,每一列都居中放置 x11 & x12 & ... & x1m\\ %第一行元素 x21 & x22 & ... & x2m\\ %第二行元素 ... & ... & ... & ...\\ xn1 & xn2 & ... & xnm\\ %第二行元素 \end{array} \right) %右括号 \end{equation} x11x21...xn1x12x22...xn2............x1mx2m...xnm
2)训练数据
训练数据K包含系统全范围的动态参数,涵盖的面一定要全,包含了开始运行、运行平稳、运行结束等阶段数据,而且一定不能包含故障数据。
K = [ X ( t 1 + i ) , X ( t 2 + i ) , X ( t k + i ) ] K=[X(t_{1+i}),X(t_{2+i}),X(t_{k+i})] K=[X(t1+i),X(t2+i),X(tk+i)]
3)记忆矩阵
从训练数据中抽取一部分代表性数据,可以组成过程记忆矩阵D,过程记忆矩阵大小为nXd,其中d表示为包含状态的数量,n表示为了观测参数的维度。
( x 1 ( t 1 ) . . . x 1 ( t d ) . . . . . . . . . x n ( t 1 ) . . . x n ( t d ) ) \begin{equation} %开始数学环境 \left( %左括号 \begin{array}{ccc} %该矩阵一共3列,每一列都居中放置 x_1(t_1) & ... & x_1(t_d)\\ %第一行元素 ... & ... & ...\\ %第二行元素 x_n(t_1) & ... & x_n(t_d)\\ %第二行元素 \end{array} \right) %右括号 \end{equation} x1(t1)...xn(t1).........x1(td)...xn(td)
4)剩余训练数据
训练数据中除去记忆矩阵的剩余部分,将会组成剩余训练数据L
5)当前系统估计矩阵
Xobs是当前系统观测矩阵,如果想要求当前系统的估计矩阵,那么就需要使用观测矩阵乘以某个大小相同的权重矩阵,即:
X e s t = D ⋅ W X_{est}=D·W Xest=D⋅W
权值矩阵W为表征状态估计和过程记忆矩阵间相似性测度的大小,为了让Xobs和Xest的残差值最小化,进行求解
6)求解过程
目标函数: m i n ϵ 2 = m i n [ ( X o b s − D ⋅ W ) T ⋅ ( X o b s − D ⋅ W ) ] 目标函数:min\epsilon^2=min[(X_{obs}-D·W)^T·(X_{obs}-D·W)] 目标函数:minϵ2=min[(Xobs−D⋅W)T⋅(Xobs−D⋅W)]
最小二乘解: W = ( D T ⋅ D ) − 1 ⋅ ( D T ⋅ D o b s ) 最小二乘解:W=(D^T·D)^{-1}·(D^T·D_{obs}) 最小二乘解:W=(DT⋅D)−1⋅(DT⋅Dobs)
大多数系统的状态数据间都会存在一定的相关性,数据之间的相关性会导致矩阵不可逆,限制了权值的求取。NSET方法利用基于相似性原理的相似性运算符代替点积,通过计算数据状态间的相似程度来表征其权值,解决数据相关所造成的矩阵不可逆。
相似性运算符号: ⊗ 相似性运算符号:\otimes 相似性运算符号:⊗
W = ( D T ⊗ D ) − 1 ⋅ ( D T ⊗ D o b s ) W=(D^T\otimes D)^{-1}·(D^T\otimes D_{obs}) W=(DT⊗D)−1⋅(DT⊗Dobs)
最终,系统当前的状态估计矩阵与观测矩阵关系如下结果:
X e s t = D ⋅ ( D T ⊗ D ) − 1 ⋅ ( D T ⊗ D o b s ) X_{est}=D·(D^T \otimes D)^{-1}·(D^T\otimes D_{obs}) Xest=D⋅(DT⊗D)−1⋅(DT⊗Dobs)
相关文章:

NSET or MSET算法--原理解析
1.背景 NSET/MSET是一种非线性的多元预测诊断技术,广泛应用于系统状态估计、故障诊断和预测等领域;相比于传统的线性模型和方法,NSET/MSET能够更好地处理非线性系统,并提供更准确的预测和诊断能力。在早期,MSET融合了…...
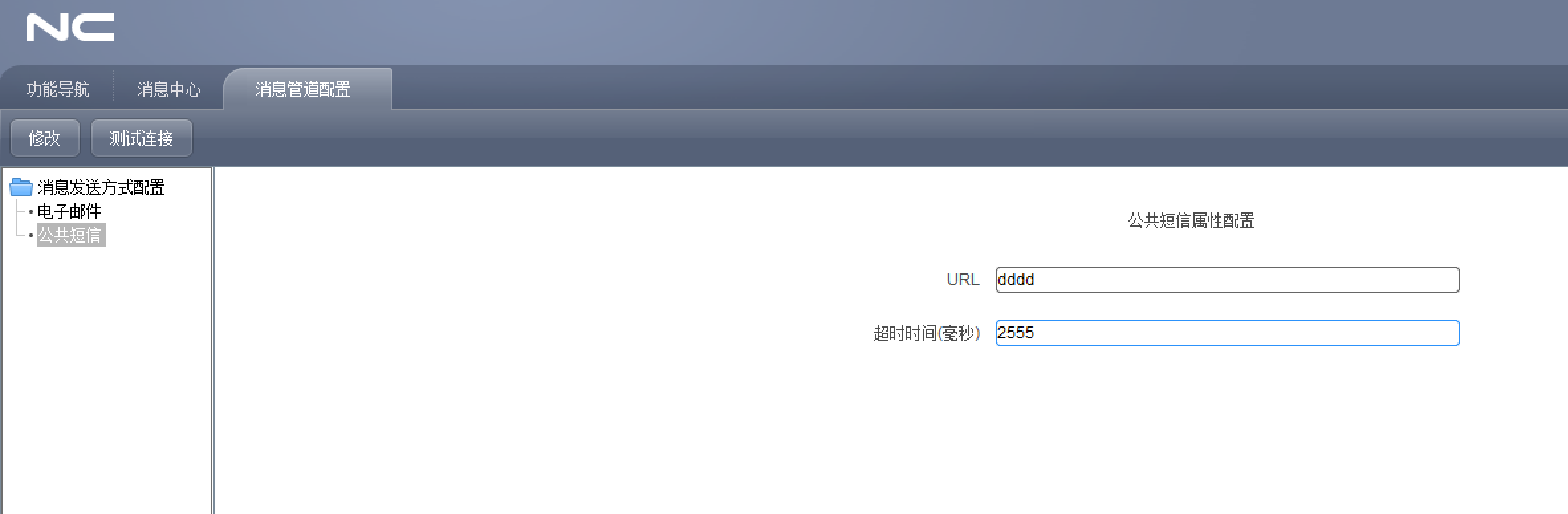
NC6 系统配置的消息渠道配置配置涉及相关的表,用户使用admin登录
NC6 系统配置的消息渠道配置配置涉及相关的表 --电子邮件、公共短信属性值配置表,比如邮箱类型、邮件发送服务器、用户、密码、发件人地址、url等。 SELECT * FROM sm_msg_stypeprop;--消息发送方式配置:电子邮件,公共短信。 SELECT * FROM sm_msg_stypebase WHERE active …...

PXC数据库性能测试对比
mysql单机 #初始化测试数据 sysbench /usr/share/sysbench/oltp_read_write.lua --mysql-host=xxx.xxx.xxx.xxx --mysql-db=test --mysql-user=hzhadmin --mysql-password=Admi --tables=10 --table-size=1000000 prepare#运行性能测试 sysbench /usr/share/sysbench/oltp_rea…...

使用AutoMySQLBackup 数据库自动备份
1.下载地址 AutoMySQLBackup的下在地址为http://sourceforge.net/projects/automysqlbackup/ 。 目前最新版本为automysqlbackup-v3.0_rc6.tar.gz 2.解压缩 把下载的automysqlbackup-v3.0_rc6.tar.gz文件拷贝到/usr/tmp下面 在/usr/local下面新建一个automysqlbackup文件夹…...

NVR批量管理软件/平台EasyNVR多个NVR同时管理支持对接阿里云、腾讯云、天翼云、亚马逊S3云存储
随着云计算技术的日益成熟,越来越多的企业开始将其业务迁移到云端,以享受更为灵活、高效且经济的服务模式。在视频监控领域,云存储因其强大的数据处理能力和弹性扩展性,成为视频数据存储的理想选择。NVR批量管理软件/平台EasyNVR&…...

13.React useTimeout
在 React 应用中,延迟执行某些操作是一个常见需求。传统的 setTimeout 在函数组件中使用可能会导致一些问题,如闭包陷阱或难以正确清理。useTimeout 钩子提供了一种声明式的方法来实现延迟执行,使得定时器的管理更加简单和可靠。这个自定义钩子不仅简化了定时器的使用,还解…...

Android待机问题与内存泄露日志定位及bugreport获取分析
文章目录 bugreportbugreport介绍获取bugreport日志分析bugreport安卓平台log获取日志android.logkernel.logkernel.log查看待机过程sysinfo.log判断内存是否有泄露分析bugreport,定位唤醒源,判断是否有ANR。分析安卓log,定位待机唤醒功耗问题,判断是否有内存泄露。bugrepo…...
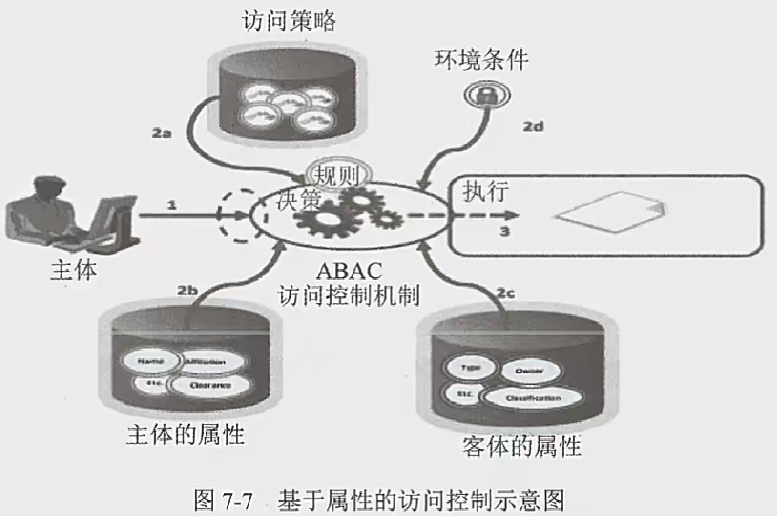
访问控制技术原理与应用
目录 访问控制概述实现访问控制目标访问控制参考模型常见访问控制模型访问控制模型-DAC自主访问控制访问控制模型-MAC强制访问控制访问控制模型-RBAC基于角色的访问控制访问控制模型-ABAC基于属性的访问控制 访问控制概述 访问控制是对资源对象的访问授权控制的方法以及运行机…...

详解Rust标准库:Vec向量
查看本地官方文档 安装rust后运行 rustup doc查看The Standard Library即可获取标准库内容 std::vec::Vec定义 Vec除了可以作为动态数组还可以模拟为一个栈,仅使用push、pop即可 Vec默认分配在堆上,对于一个容量为4,有两个元素a、b的向量…...
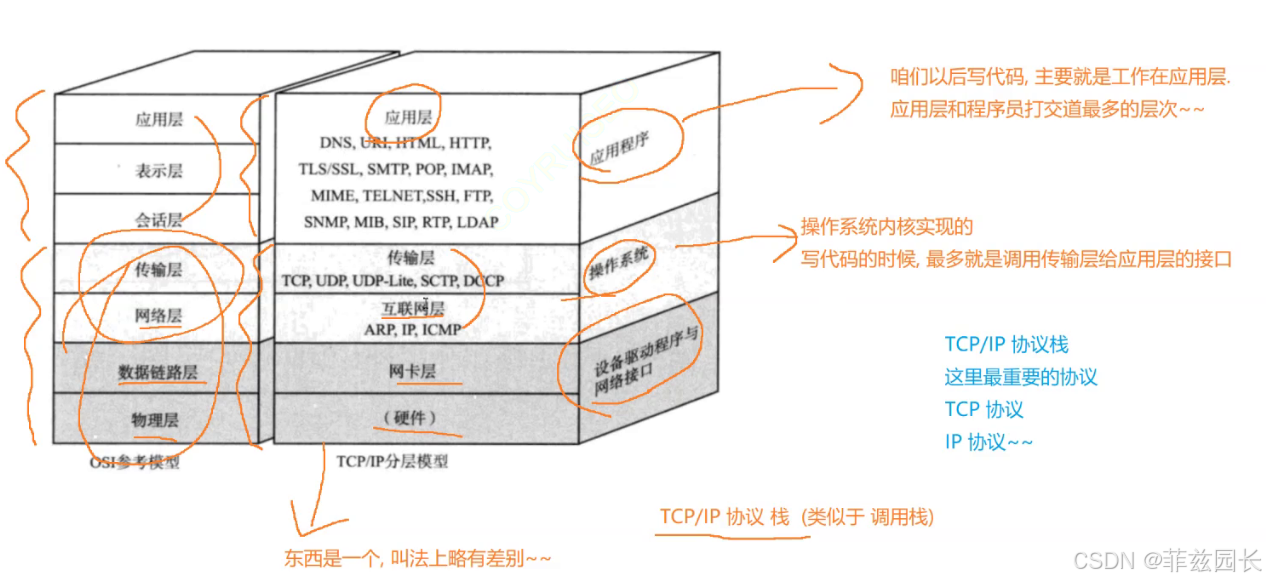
网络原理(初一,TCP/IP五层(或四层)模型面试问题)
TCP/IP五层(或四层)模型 TCP/IP是⼀组协议的代名词,它还包括许多协议,组成了TCP/IP协议簇。 TCP/IP通讯协议采⽤了5层的层级结构,每⼀层都呼叫它的下⼀层所提供的⽹络来完成⾃⼰的需求。 • 应⽤层:负责…...

Unity引擎材质球残留贴图引用的处理
大家好,我是阿赵。 这次来分享一下Unity引擎材质球残留贴图引用的处理 一、 问题 在使用Unity调整美术效果的时候,我们很经常会有这样的操作,比如: 1、 同一个材质球切换不同的Shader、 比如我现在有2个Shader,…...

Flutter鸿蒙next中封装一个列表组件
1. 创建Flutter项目 首先,确保你已经安装了Flutter SDK,并创建一个新的Flutter项目: flutter create podcast_app cd podcast_app2. 封装列表组件 我们将在lib目录下创建一个新的文件,命名为podcast_list.dart,用于…...
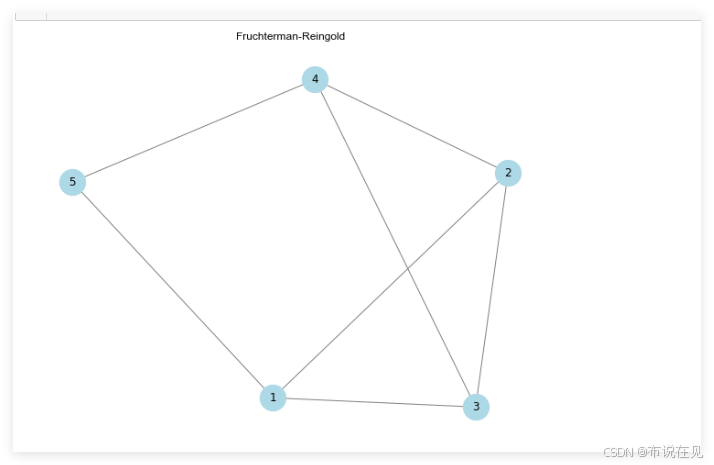
层次与网络的视觉对话:树图与力引导布局的双剑合璧
目录 目的内容树图绘制目的步骤参考代码结果与分析 力引导布局算法目的参考代码结果与分析 总结 目的 掌握常用可视化软件与工具:学习和熟练使用常用的数据可视化软件和工具,如Matplotlib、Seaborn、Plotly、Tableau等。这些工具提供了用于创建图表、图…...
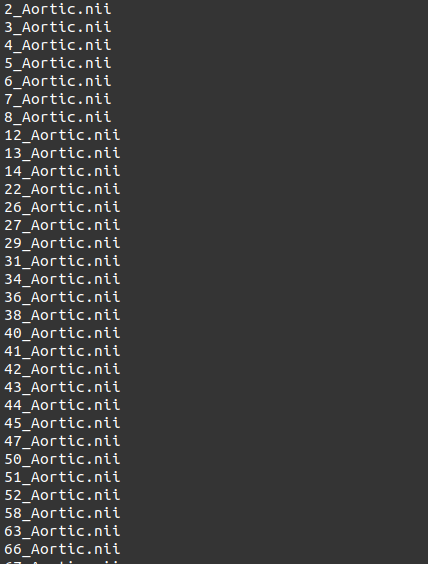
python将数据集中所有文件名升序制作txt文件(医学影像)
import os import re # 设定图像文件所在的路径 img_path ./2d/images/ #需修改路径 # 获取该路径下的所有文件名 img_list os.listdir(img_path) # 过滤出以.nii结尾的文件名 nii_list [f for f in img_list if f.endswith(.nii)] # 使用正则表达式从文件名中提…...

【The Art of Unit Testing 3_自学笔记06】3.4 + 3.5 单元测试核心技能之:函数式注入与模块化注入的解决方案简介
文章目录 3.4 函数式依赖注入技术 Functional injection techniques3.5 模块化依赖注入技术 Modular injection techniques 写在前面 上一篇的最后部分对第三章后续内容做了一个概括性的梳理,并给出了断开依赖项的最简单的实现方案,函数参数值注入法。本…...
【VSCode】配置
安装插件 C vscode-icons gdb调试 https://www.bilibili.com/video/BV15U4y1x7b2/?spm_id_from333.999.0.0&vd_sourcedf0ce73d9b9b61e6d4771898f1441f7f https://www.bilibili.com/video/BV1pU4y1W74Z?spm_id_from333.788.recommend_more_video.-1&vd_sourcedf0…...

Linux 常用命令整理大全及命令使用心得
本文章是为了总结自己用过的命令,以及一些心得,网上有很多类似的,但自己总结才能更好的理解。 文章目录 一、文件和目录管理01、 ls :列出目录内容02、cd:更改当前目录03、pwd:显示当前工作目录04、mkdir&a…...

计算器的实现
计算器的⼀般实现 计算器的一般实现:优化:使⽤函数指针数组的实现: 计算器的一般实现: #include <stdio.h> int add(int a, int b) {return a b; } int sub(int a, int b) {return a - b; } int mul(int a, int b) {retur…...
这个工具帮你快速实现数据集成和同步
在这个信息爆炸的时代,数据的流动和同步逐渐成为企业运营的命脉。然而,企业正面临着前所未有的数据挑战,无论是跨地域的分公司协作,还是云服务与本地数据库的交互,数据的集成、清洗、转换和加载(ETL&#x…...

论文阅读:Computational Long Exposure Mobile Photography (一)
这篇文章是谷歌发表在 2023 ACM transaction on Graphic 上的一篇文章,介绍如何在手机摄影中实现长曝光的一些拍摄效果。 Abstract 长曝光摄影能拍出令人惊叹的影像,用运动模糊来呈现场景中的移动元素。它通常有两种模式,分别产生前景模糊或…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...
