算法【Java】—— 动态规划之斐波那契数列模型
动态规划
动态规划的思路一共有五个步骤:
- 状态表示:由经验和题目要求得出,这个确实有点抽象,下面的题目会带大家慢慢感受状态标识
- 状态转移方程
- 初始化:避免越界访问 dp 表,所以在进行填表之前我们要预先填写好一些数据。
- 填表顺序
- 返回值
动态规划的代码书写步骤:
建表,初始化,填表,返回值,最后中间可能由细节的处理
实战演练
第N个泰波那契数

解析:对于一维的数据我们的状态表示基本是题目要求什么状态表示就是什么,上面这个题目要求我们求出第N 个泰波那契数,那么我们的 dp 表就定义为 dp[i] 表示 第 i 个 泰波那契数。
状态转移方程:题目已经很贴心告诉我们 T(n + 3) = T(n) + T(n+1) + T(n+2),我们稍微转化一下:T(n) = T(n-3) + T(n-2) + T(n-1),即 dp[i] = dp[i-1] + dp[i-2] + dp[i-3]
初始化:我们在求 dp[0]、dp[1]、dp[2] 的时候是不能直接使用状态转移方程来求取的,否则就会发生数组越界,所以我们要在填表之前把着三个 dp 值给预设好,dp[0] = 0, dp[1] = dp[2] = 1
填表顺序:由于在初始化我们已经填好了前面三个数字:dp[0]、dp[1]、dp[2],所以我们从 i == 3 开始填表,从左向右这个顺序把 dp 表填满。
返回值:题目要求我们求 第N 个泰波那契数,正好我们的 dp 表的状态表示也是这个,所以直接返回 dp[n] .
细节处理:如果 n = 0 / 1 的时候,直接返回,不需要初始化和填表了,避免数组访问越界,举个例子:假设 n 等于 0,也就是说 dp 表其实就只有一个位置,但是你初始化要初始三个位置,数组妥妥越界访问。
class Solution {public int tribonacci(int n) {//建表int[] dp = new int[n + 1];//细节处理if(n == 0 || n == 1) return n;//初始化dp[0] = 0; dp[1] = 1; dp[2] = 1;//填表for(int i = 3; i <= n; i++) {dp[i] = dp[i-1] + dp[i-2] + dp[i-3];}//返回值return dp[n];}
}
三步问题

解析:
状态表示:一维数组形式,我们通常以题目要求出来思考状态表示,如果这个状态表示不能推导出状态转移方程那就再换别的状态表示,这里我们直接定义状态表示为 dp[i] 表示上到第 i 个台阶一共有多少中方式。
状态转移方程:上到 第 i 个台阶有多少种方式 等于上到第 i - 1 个台阶需要多少种方式 + 上到第 i - 2 个台阶需要多少种方式 + 上到第 i - 3 个台阶需要多少种方式,为什么是三种台阶方式相加,回到题目,一次可以跨一步 / 两步 / 三步。
初始化,我们需要将 dp[1] = 1, dp[2] = 2,dp[3] = 4,设置好,同样这里也有细节要处理,如果 n == 1 或者 n == 2 直接返回即可。
填表顺序:从 i == 4 开始填,从左到右
返回值:直接返回 dp[n]
这道题还有一个小细节,就是结果可能很大,我们需要将结果 取模 1000000007,在每次进行加法的时候都去取模即可。
class Solution {public int waysToStep(int n) {//建表int[] dp = new int [n+1];//细节处理if(n == 1 || n == 2) return n;//初始化dp[1] = 1; dp[2] = 2; dp[3] = 4;//填表for(int i = 4; i <= n; i++) {dp[i] = ((dp[i-1] + dp[i-2]) % 1000000007 + dp[i-3]) % 1000000007;}//返回值return dp[n]; }
}
使用最小花费爬楼梯

解析:
状态表示:这里还是一个一维形式的数组,我们定义 dp[i] 表示达到 第 i 个台阶所需要的最小花费。
状态转移方程:由于每次可以走一个或者两个台阶,所以我们要推导出 dp[i] ,就要知道 dp[i-1] + cost[i-1] 和 dp[i-2] + cost[i-2] 的最小花费是什么。这个为什么要加上 cost[i-1] / cost[i-2] ? 因为 dp[i] 表示达到 i 台阶需要的最小花费,你如果从 i 台阶往上走就需要先支付 i 台阶的费用也就是 cost[i]。
初始化:dp[1] = 0,dp[2] = 0,由于Java创建数组的时候默认值就是 0,所以可以不进行初始化了,但是细节还是要处理的,如果 n == 0 || n == 1 直接返回 n。
填表顺序:从 i == 2 开始从左往右填
返回值:dp[n]
class Solution {public int minCostClimbingStairs(int[] cost) {//建表int n = cost.length;int[] dp = new int[n+1];//细节处理if(n == 0 || n == 1) return n;//填表for(int i = 2; i <= n; i++) {dp[i] = Math.min(dp[i-1] + cost[i-1], dp[i-2] + cost[i-2]);}return dp[n];}
}
解码方式


解析:
状态表示:到达第 i 个字符的时候一共有多少种编码。
状态转移方程:首先我们先进行单字符解码,如果一个字符的数值不等于 0 的时候,是可以单独解码的,这时候 dp[i] += dp[i-1],把前一个字符有多少种解码方式加起来。
然后就是和前一个字符看是否能共同解码,首先要求前一个字符不能为 0, 其次两个字符组成的数字要小于等于 26,如果都满足,说明可以和前一个字符进行合并解码,dp[i] += dp[i-2],把前前一个字符的解码方式相加起来。
初始化:先处理前两个字符的 dp 值,并且有一个细节,如果 字符串长度为 1, 是不能进行第二个字符的解码的,需要直接返回。
填表顺序:从 i == 2 开始从左往右填写。
返回值:dp[n-1]
还有一个细节:如果一个dp 值为 0 的时候,不需要进行后面的填表操作,此时已经无法对字符串进行解码了,直接返回 0 即可。
class Solution {public int numDecodings(String ss) {//建表int n = ss.length();int[] dp = new int [n];char[] s = ss.toCharArray();//细节处理与初始化if(s[0] - '0' != 0) {dp[0] = 1;} else {dp[0] = 0;}if(n == 1 || dp[0] == 0) {return dp[0];}//处理第二个字符if(s[1] - '0' != 0) dp[1]++;if(s[0] - '0' != 0 && (s[0] - '0') * 10 + (s[1] - '0') <= 26) dp[1]++;//填表for(int i = 2; i < n; i++) {if(s[i] - '0' != 0) dp[i] += dp[i-1];if(s[i-1] - '0' != 0 && 10 * (s[i-1] - '0') + (s[i] - '0') <= 26) dp[i] += dp[i-2];if(dp[i] == 0) return 0;}return dp[n-1];}
}
小结
面对一维形式的数据的时候,一般我们的状态表示直接从题目要求中获取。
在初始化之前一定要注意没有细节需要处理。
相关文章:

算法【Java】—— 动态规划之斐波那契数列模型
动态规划 动态规划的思路一共有五个步骤: 状态表示:由经验和题目要求得出,这个确实有点抽象,下面的题目会带大家慢慢感受状态标识状态转移方程初始化:避免越界访问 dp 表,所以在进行填表之前我们要预先填…...

idea连接docker并构建镜像
安装docker 安装docker idea连接docker 安装docker插件 设置docker连接 设置docker.exe 这个docker.exe是为了运行docker,可以通过安装docker desktop获取 docker desktop下载地址 右键图标找到文件位置 在同级的resource中 编写Dockerfile # 使用官方 Nginx…...

百度如何打造AI原生研发新范式?
👉点击即可下载《百度AI原生研发新范式实践》资料 2024年10月23-25日,2024 NJSD技术盛典暨第十届NJSD软件开发者大会、第八届IAS互联网架构大会在南京召开。本届大会邀请了工业界和学术界的专家,优秀的工程师和产品经理,以及其它行…...

RedisTemplate类中的常用方法粗解(简单明了,预计5分钟看完)
在阅读项目代码过程中发现引用RedisTemplate 的方法操作redis时,都会有一些特定的ops ,对此好奇就查资料的情况下有了本博客。 操作之前付一张我们项目中的用到的地方的图 另外本文中的语言用到的是Java,附上试验用到的redisTemplete依赖 <…...

鸿蒙ArkTS中的布局容器组件(Column、Row、Flex、 Stack、Grid)
在鸿蒙ArkTS中,布局容器组件有很多,常见的有: ⑴ Column:(垂直布局容器):用于将子组件垂直排列。 ⑵ Row:(水平布局容器):用于将子组件水…...

显存占用 显存测试
目录 显存测试 显存占用示例 一个模型多卡占用 显存测试 import torch# 计算张量的大小(例如:每个 float 占用 4 字节) # 40GB 40 * 1024 * 1024 * 1024 字节 # 每个 float 4 字节,因此需要的 float 数量为 (40 * 1024 * 1024…...

快速入门CSS
欢迎关注个人主页:逸狼 创造不易,可以点点赞吗 如有错误,欢迎指出~ 目录 CSS css的三种引入方式 css书写规范 选择器分类 标签选择器 class选择器 id选择器 复合选择器 通配符选择器 color颜色设置 border边框设置 width/heigth 内/外边距 C…...
)
AcWing 1073 树的中心 树形dp (详解)
这道题目非常有新意,在过去,我们通常先访问子节点去更新父节点的状态,但是这道题我们还需要从父节点去更新子节点。 我们可以想象为向上和向下两个方向,我们任取一点,先向下走,再回来更新上面的点…...

modelscope下载Qwen2.5 72B 模型方法
conda create -n modelscope python=3.10 conda activate modelscopepip install modelscope执行这个python代码: from modelscope.hub.snapshot_download import snapshot_download# 下载模型到当前路径 model_dir = snapshot_download(...
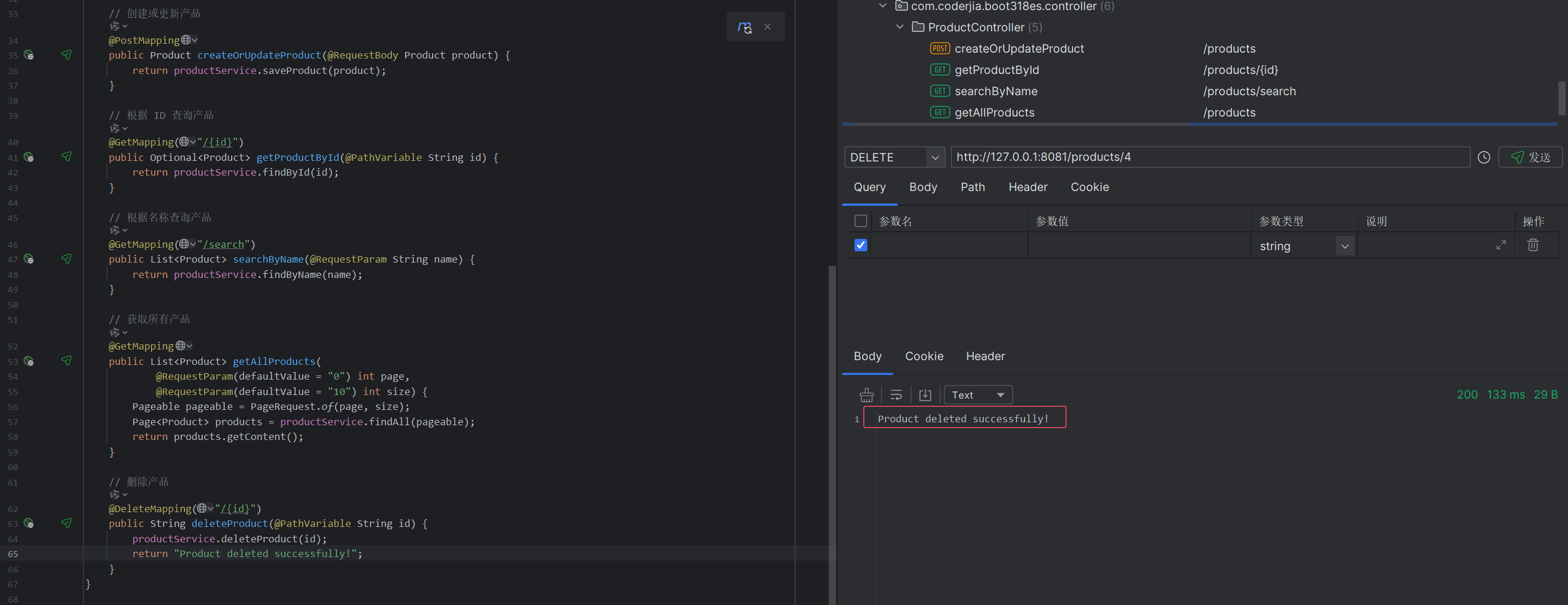
重学SpringBoot3-整合 Elasticsearch 8.x (二)使用Repository
更多SpringBoot3内容请关注我的专栏:《SpringBoot3》 期待您的点赞👍收藏⭐评论✍ 整合 Elasticsearch 8.x (二)使用Repository 1. 环境准备1.1 项目依赖1.2 Elasticsearch 配置 2. 使用Repository的基本步骤2.1 创建实体类2.2 创…...

为什么说模拟电路的难点就在开通过程和关断过程?难在什么地方?
模拟电路中开通过程和关断过程之所以困难,主要有以下几个方面的原因: 1. 瞬态响应特性复杂 - 在开通和关断瞬间,电路中的电流和电压会发生快速变化,产生复杂的瞬态响应。这些瞬态响应可能包含过冲、下冲、振铃等现象,…...

CubeIDE BUG-project‘hello‘has no explict encoding set hello
projecthellohas no explict encoding set hello 解决方法: 点击红色处注册账号后登录,删除原本文件后重新生成即可。...

在线PDF转图片网站
https://www.ilovepdf.com/download/qgxkmbzgxt6yb3s8l9f7fc3q9606hq0bfh4b33mnrf3p7tp8l0d4qy386b5dxqwjbhq7j3j4tp20m4dnb89wA9jjw25br1gtAw42l0m1sq047nvld4qqrm8kzjplkAhw9458p4wjgbmn08g49l23c1khsggdx4A7z3m9xh19mgzdlllyA6r1/52 在线excel转图片 https://www.zamzar.c…...

ps和top的区别
时间上的区别: ps是静态查看进程而top是动态持续监控进程 功能上的区别 ps只是查看进程,top还可以监视系统性能,如平均负载,cpu和内存的消耗 ps 常用格式:ps -ef (ef简洁aux详细 System V风格和BSD 风格) | grep P…...

自动驾驶上市潮中,会诞生下一个“英伟达”吗?
站上科技创新潮头的企业总是备受资本青睐。20世纪开始,从IT到互联网,IBM、英特尔、微软、苹果等各大科技巨头,你方唱罢我登场。 近几年,人工智能成为资本市场新传奇故事的孕育之地。今年10月,英伟达市值首度突破3.5万…...

CSS 计数器:深入解析与高级应用
CSS 计数器:深入解析与高级应用 CSS 计数器是前端开发中一个强大但经常被忽视的功能。它们允许开发者创建和管理自定义的计数序列,这在处理复杂文档结构时尤其有用。本文将深入探讨 CSS 计数器的原理、用法,并展示一些高级应用示例。 什么是…...

【真题笔记】15年系统架构设计师要点总结
【真题笔记】15年系统架构设计师要点总结 分布式数据库中各种透明RAID 5IPv6 IPv4电子商务系统项目配置管理IPO图(输入加工输出图)桥接模式的UML图面向对象设计原则软件测试 在15年真题练习中,对错题模棱两可的考点进行重点记录与内容延申。…...
)
斗破C++编程入门系列之三十九:多态性:纯虚函数和抽象类(四星斗师)
斗破C目录: 斗破C编程入门系列之前言(斗之气三段) 斗破C编程入门系列之二:Qt的使用介绍(斗之气三段) 斗破C编程入门系列之三:数据结构(斗之气三段) 斗破C编程入门系列之…...

目前美国的互联网环境
随着科技的迅猛发展,互联网已经成为了现代社会不可或缺的一部分。作为全球科技创新的领导者之一,美国在互联网领域拥有着丰富的资源和先进的技术。本文将对美国目前的互联网环境进行探讨,包括网络基础设施、网络安全、数字经济以及互联网对社…...

从最小作用量原理推导牛顿三大定律
从最小作用量原理推导牛顿三大定律 引言 在物理学中,牛顿三大定律是描述经典力学中物体运动的基本定律。然而,这些定律并不是孤立存在的,它们可以从一个更为普遍的原理——最小作用量原理中推导出来。最小作用量原理是一个深刻而优雅的理论…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...
