机器学习3_支持向量机_线性不可分——MOOC
线性不可分的情况
如果训练样本是线性不可分的,那么上一节问题的是无解的,即不存在 和
满足上面所有N个限制条件。
对于线性不可分的情况,需要适当放松限制条件,使得问题有解。
放松限制条件的基本思路:
对每个训练样本及标签
设置松弛变量(slack variable)
对于线性不可分情况,需适当放松限制条件
限制条件改写:
改造后的支持向量机优化版本
最小化: 或
限制条件:
(1)
(2)
- 以前的目标函数只需要最小化
,现在的目标函数增加了一项 所有
的和。
- 比例因子
平衡两项
比例因子 是人为设定的。
人为事先设定的参数叫做算法的超参数(Hyper Parameter)
实际中:不断变化 的值
同时测试算法的识别率
选取超参数
一个算法中,选取的超参数 越多,意味着算法需要手动调整优化的地方也就越多,这样算法的自动性也会降低。
支持向量机是超参数很少的算法模型。
超参数很多的算法模型,如人工神经网络、卷积神经网络等。
在线性不可分情况下应用支持向量机
取目标函数:
是为了超平面和线性可分情况保持基本一致
以下是训练数据以及解出的分类面的展示

可以看到这个分类面分开大多数的圆圈和叉,只在一个训练样本上存在分类的错误。
有了线性不可分情况下的支持向量机算法

如图,这个解分错了将近一半的样本,这个解远远不能让人满意。
问题在于我们的算法模型是线性的。也就是,我们假设分开两类的函数是直线或者超平面,我们是在一组直线和超平面中选择最合适分开这两类数据的直线或者超平面。但线性模型的表现力是不够的。
在下图这个例子中,可以看到能够分开这两类的是某种曲面,例如这个椭圆,而不是直线。

因此,我们只有想办法扩大可选函数的范围,使它超越线性,才有可能应对各种复杂的线性不可分的情况。
低维到高维的映射
支持向量机在扩大可选函数范围方面独树一帜。
其他算法,如人工神经网络、决策树等,采用的是直接产生更多可选函数的方式。

例如上图,在人工网络中,通过多层非线性函数的组合能够产生类似于椭圆这样的曲线,从而分开这幅图中的圆圈和叉。
而支持向量机却不是直接产生这样的函数,而是通过将特征空间由低维映射到高维,然后在高维的特征空间当中用线性超平面对数据进行分类。

、
是图中的❌,
、
是图中的⭕️
这个例子是线性不可分的
如果我们构造一个二维到五维到映射
按照这个映射,可以解出、
、
、
当映射变成五维时,、
、
、
线性可分
设:
可以算出
由于、
是同一类,
、
是同一类
人为二维到五维到映射 ,线性不可分的数据集
线性可分的数据集
假设:
在一个M维空间上随机取N个训练样本,随机的对每个训练样本赋予标签
或
假设:
这些训练样本线性可分的概率为
则
当
趋于无穷大时,
即,当我们增加特征空间的维度 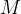 的时候,超平面待估计的参数
的时候,超平面待估计的参数  的维度也会增加。也就是整个算法模型的自由度会增加。
的维度也会增加。也就是整个算法模型的自由度会增加。
这个定理告诉我们,将训练样本由低维映射到高维 增大线性可分的概率。
相关文章:
机器学习3_支持向量机_线性不可分——MOOC
线性不可分的情况 如果训练样本是线性不可分的,那么上一节问题的是无解的,即不存在 和 满足上面所有N个限制条件。 对于线性不可分的情况,需要适当放松限制条件,使得问题有解。 放松限制条件的基本思路: 对每个训…...

bash: git: command not found
在windows上重新安装Git之后,遇到cmd可以使用git命令,但是git bash中使用的git命令的时候,会提示: $ git bash: git: command not found 解决办法 找到用户目录下的.bash_profile和.bashrc文件,编辑打开,找…...

大模型LLama3!!!Ollama下载、部署和应用(保姆级详细教程)
首先呢,大家在网站先下载ollama软件 这就和anaconda和python是一样的 废话不多说 直接上链接:Download Ollama on Windows 三个系统都支持 注意: 这里的Models,就是在上面,大家点开之后,里面有很多模型…...

ReactPress系列—NestJS 服务端开发流程简介
ReactPress Github项目地址:https://github.com/fecommunity/reactpress 欢迎提出宝贵的建议,感谢Star。 NestJS 服务端开发流程简介 NestJS 是一个用于构建高效、可靠和可扩展的服务器端应用程序的框架。它使用 TypeScript(但也支持纯 Java…...

Maven 下载配置 详解 我的学习笔记
Maven 下载配置 详解 我的学习笔记 一、Maven 简介二、maven安装配置三、maven基本使用四、idea配置mavenidea配置maven环境maven坐标idea创建maven项目配置Maven-Helper插件 五、依赖管理 一、Maven 简介 Apache Maven 是一个项目管理和构建工具,它基于项目对象模型…...

【学术精选】SCI期刊《Electronics》特刊“New Challenges in Remote Sensing Image Processing“
英文名称:New Challenges in Remote Sensing Image Processing 中文名称:"遥感图像处理的新挑战"特刊 期刊介绍 “New Challenges in Remote Sensing Image Processing”特刊隶属于《Electronics》期刊,聚焦遥感图像处理领域快速…...

卷积神经网络——pytorch与paddle实现卷积神经网络
卷积神经网络——pytorch与paddle实现卷积神经网络 本文将深入探讨卷积神经网络的理论基础,并通过PyTorch和PaddlePaddle两个深度学习框架来展示如何实现卷积神经网络模型。我们将首先介绍卷积神经网络、图像处理的基本概念,这些理论基础是理解和实现卷…...

云平台虚拟机运维笔记整理,使用libvirt创建和管理虚拟机,以及开启虚拟机嵌套,虚拟磁盘扩容,物理磁盘扩容等等
云平台虚拟机运维笔记整理,使用libvirt创建和管理虚拟机,以及开启虚拟机嵌套,虚拟磁盘扩容,物理磁盘扩容等等。 掌握和使用qemu和libvirt,分别使用它们创建一个cirros虚拟机,并配置好网络。 宿主机node0的系统为ubuntu16,IP为192.168.56.200。 qemu和libvirt简介 QEMU…...

最佳实践:如何实现函数参数之间的TS类型相依赖和自动推断
引入 最近在开发一款极致优雅的前端状态管理库AutoStore时碰到这样一个问题。 拟实现Field组件,该组件相关类型简化代码如下: type Field (props:{validate,render:(props:{value,isValid}) })该组件,具有validate和render两个属性: 其中…...

Linux基础指令1
好久没写博客了,这次我将重新做人,每星期都更,做不到的话直接倒立洗头。最近在学Linux,感觉很厉害的样子,先浅学一下再弄数据结构去。 Linux的基本操作是通过指令来执行的,所以我们先来学习下指令。 1.简…...

软件设计师:排序算法总结
一、直接插入 排序方式:从第一个数开始,拿两个数比较,把后面一位跟前面的数比较,把较小的数放在前面一位 二、希尔 排序方式:按“增量序列(步长)”分组比较,组内元素比较交换 假设…...
「Mac畅玩鸿蒙与硬件25」UI互动应用篇2 - 计时器应用实现
本篇将带领你实现一个实用的计时器应用,用户可以启动、暂停或重置计时器。该项目将涉及时间控制、状态管理以及按钮交互,是掌握鸿蒙应用开发的重要步骤。 关键词 UI互动应用时间控制状态管理用户交互 一、功能说明 在这个计时器应用中,用户…...

计算机专业开题报告写法,该怎么写好?
不会写开题报告,或者想要一些论文模版的,欢迎评论,会第一时间给大家。 题报告是计算机专业大学毕业生在开展毕业设计或论文研究前,对研究课题进行详细介绍和计划的重要环节。作为开题者对科研课题的一种文字说明,开题…...

Vue(JavaScript)读取csv表格并求某一列之和(大浮点数处理: decimal.js)
文章目录 想要读这个表格,并且求第二列所有价格的和方法一:通过添加文件输入元素上传csv完整(正确)代码之前的错误部分因为价格是小数,所以下面的代码出错。如果把parseFloat改成parseInt,那么求和没有意义…...

Pyraformer复现心得
Pyraformer复现心得 引用 Liu, Shizhan, et al. “Pyraformer: Low-complexity pyramidal attention for long-range time series modeling and forecasting.” International conference on learning representations. 2021. 代码部分 def long_forecast(self, x_enc, x_m…...

成绩排序c++
说明 给出了班里某门课程的成绩单,请你按成绩从高到低对成绩单排序输出,如果有相同分数则名字字典序小的在前。 输入格式 第一行为nn(0<n<200<n<20),表示班里的学生数目; 接下来的nn行,每行为每个学生的名字和他的…...
人脸检测之MTCNN算法网络结构
MTCNN(Multi-task Cascaded Convolutional Networks)是一种用于人脸检测和关键点检测的深度学习模型,特别适合在复杂背景下识别出多尺度的人脸。它通过多任务学习来实现人脸检测和人脸关键点定位(如眼睛、鼻子、嘴巴的位置&#x…...
)
蓝桥杯顺子日期(填空题)
题目:小明特别喜欢顺子。顺子指的就是连续的三个数字:123、456 等。顺子日期指的就是在日期的 yyyymmdd 表示法中,存在任意连续的三位数是一个顺子的日期。例如 20220123 就是一个顺子日期,因为它出现了一个顺子:123&a…...

Java云HIS医院管理系统源码 病案管理、医保业务、门诊、住院、电子病历编辑
云HIS系统优势 (1)客户/用户角度 无需安装,登录即用 多终端同步,轻松应对工作环境转换 系统使用简单、易上手,信息展示主次分明、重点突出 极致降低用户操作负担:关联功能集中、减少跳转,键盘快…...

【C++的vector、list、stack、queue用法简单介绍】
【知识预告】 vector的介绍及使用list的介绍及使用list与vector的对比stack的介绍和使用queue的介绍和使用priority_queue的介绍和使用 1 vector的介绍及使用 1.1 vector的介绍 vector是表示可变大小数组的序列容器和数组类似,vector也采用连续存储空间来存储元…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...
