LeetCode34:在排序数组中查找元素第一个和最后一个位置
原题地址:. - 力扣(LeetCode)
题目描述
给你一个按照非递减顺序排列的整数数组
nums,和一个目标值target。请你找出给定目标值在数组中的开始位置和结束位置。如果数组中不存在目标值
target,返回[-1, -1]。你必须设计并实现时间复杂度为
O(log n)的算法解决此问题。示例 1:
输入:nums = [5,7,7,8,8,10], target = 8 输出:[3,4]示例 2:
输入:nums = [5,7,7,8,8,10], target = 6 输出:[-1,-1]示例 3:
输入:nums = [], target = 0 输出:[-1,-1]提示:
0 <= nums.length <= 105-109 <= nums[i] <= 109nums是一个非递减数组-109 <= target <= 109
解题思路
二分查找:我们使用二分查找来查找目标值的左边界和右边界。在给定的有序数组中,使用二分查找可以减少搜索范围,从而达到 O(log n) 的时间复杂度。
- 左边界查找:我们在二分查找时,使用一个标志
lower来指示我们是查找目标值的左边界还是右边界。
- 如果
lower为true,则我们会在目标值的位置停止时继续往左移动,从而找到目标值的最左边位置。- 如果
lower为false,则我们会在目标值的位置停止时继续往右移动,直到目标值的右边界。返回结果:通过两次二分查找分别获取左边界和右边界的索引。如果左边界小于等于右边界,并且这两个位置上的值都等于目标值,则返回这两个索引;否则,返回
[-1, -1]。
源码实现
class Solution {public int[] searchRange(int[] nums, int target) {// 1. 使用二分查找找到目标值的左边界(lower = true)int leftIdx = binarySearch(nums, target, true);// 2. 使用二分查找找到目标值的右边界(lower = false),然后减去 1 获取实际的右边界int rightIdx = binarySearch(nums, target, false) - 1;// 3. 检查左边界和右边界是否有效,且这两个位置上的值是否为目标值if (leftIdx <= rightIdx && rightIdx < nums.length && nums[leftIdx] == target && nums[rightIdx] == target) {// 4. 返回目标值的左边界和右边界return new int[]{leftIdx, rightIdx};} // 5. 如果目标值不存在,返回 [-1, -1]return new int[]{-1, -1};}// 这里的 lower 参数用于控制是查找左边界(true)还是右边界(false)public int binarySearch(int[] nums, int target, boolean lower) {// 1. 初始化二分查找的左右边界int left = 0, right = nums.length - 1;// 2. 默认返回的答案是 nums.length,这样当目标值不存在时,能保证返回 [-1, -1]int ans = nums.length;while (left <= right) {int mid = (left + right) / 2;// 3. 根据目标值与中间值的比较来更新搜索范围// 4. 如果目标值小于中间值,或者是查找左边界时(lower = true)中间值大于等于目标值,// 则将搜索范围缩小到左半部分if (nums[mid] > target || (lower && nums[mid] >= target)) {right = mid - 1;ans = mid;} else {// 5. 如果目标值大于中间值,则搜索范围缩小到右半部分left = mid + 1;}}// 6. 返回找到的索引位置(若没有找到,则返回 nums.length)return ans;}
}
复杂度分析
时间复杂度:
- 每次调用
binarySearch都是 O(log n),其中n是数组的长度。- 在
searchRange方法中,调用了两次binarySearch,一次查找左边界,另一次查找右边界。因此总时间复杂度为 O(log n)。空间复杂度:
- 该算法只使用了常量级的额外空间(除了返回结果数组),因此空间复杂度是 O(1)。
相关文章:

LeetCode34:在排序数组中查找元素第一个和最后一个位置
原题地址:. - 力扣(LeetCode) 题目描述 给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。 如果数组中不存在目标值 target,返回 [-1, -1]。 你必须…...

汽车广告常见特效处理有哪些?
汽车广告作为展示汽车性能和外观的重要媒介,常常需要借助特效来增强视觉效果,吸引观众的注意力。以下是一篇关于汽车广告中常见特效处理的文章。 在竞争激烈的汽车市场中,广告不仅是推广产品的工具,更是艺术和科技的结合。特效技…...

Unexpected response code: 400解决
原因:Nginx配置错误,业务服务提供了 websocket 服务,基于 websocket 来实现报表数据的推送,客户在浏览器上查看报表,经过 http 代理将请求传递给后端服务。 解决方案 Nginx中增加websocket配置 location ~/websocket…...

世优科技携手人民中科打造AI数字人智能体助力智慧校园
近日,世优科技与人民中科携手,为中国劳动关系学院开发了一款AI数字人助手,不仅在校园内部承担日常问询、交互工作,还在学校的展厅中担任讲解员的角色,为师生们提供生动详尽的导览服务。 中国劳动关系学院作为中华全国总…...

Mac intel 安装IDEA激活时遇到问题 jetbrains.vmoptions.plist: Permission denied
激活时执行脚本, permission denied ➜ scripts ./install.sh ./install.sh: line 31: /Users/dry/Library/LaunchAgents/jetbrains.vmoptions.plist: Permission deniedjetbrains.vmoptions.plist 这个文件没权限,打开看了一下 install.sh 这…...

区块链应用第1讲:基于区块链的智慧货运平台
基于区块链的智慧货运平台 网络货运平台已经比较成熟,提供了给货源方提供找司机的交易匹配方案;其中包含这几个角色:货主、承运人(司机、车队长)、监管机构、平台。司机要想接单,依赖于多个中心化的第三方平台,且三方平…...

量化交易系统开发-实时行情自动化交易-风险控制
19年创业做过一年的量化交易但没有成功,作为交易系统的开发人员积累了一些经验,最近想重新研究交易系统,一边整理一边写出来一些思考供大家参考,也希望跟做量化的朋友有更多的交流和合作。 接下来继续说说风险控制模块࿰…...

深入探索 Seaborn:高级绘图的艺术与实践
引言 在数据科学领域,数据可视化是至关重要的一步。它不仅能够帮助我们更好地理解数据,还能有效地传达信息,支持决策过程。Seaborn 是一个基于 Matplotlib 的高级 Python 数据可视化库,它提供了许多高级绘图功能,使得…...
《现代工业经济和信息化》是什么级别的期刊?是正规期刊吗?能评职称吗?
问题解答: 问:《现代工业经济和信息化》是不是核心期刊? 答:不是,是知网收录的正规学术期刊。 问:《现代工业经济和信息化》级别? 答:省级。主管单位:山西省工业和…...

【TS】九天学会TS语法——2.TypeScript基本类型及变量声明
今天学习的内容是TypeScript 基本类型,包括 number, string, boolean, any, void 等,以及变量声明的方式和区别。 基本类型介绍变量声明(var, let, const)类型注解 开始学习 目录 引言 一、基本类型介绍 二、变量声明 1.概念解析 …...

html+js+css实现拖拽式便签留言
前些日子在网上冲浪时,看到一个便签式留言墙,让人耳目一新。心想这个看着不错,额想要。于是便开始搜寻是否有相应开源插件,想将其引入自己的博客中。但是搜寻了一圈,都没有符合预期的,要么功能不符合。有的功能符合&am…...
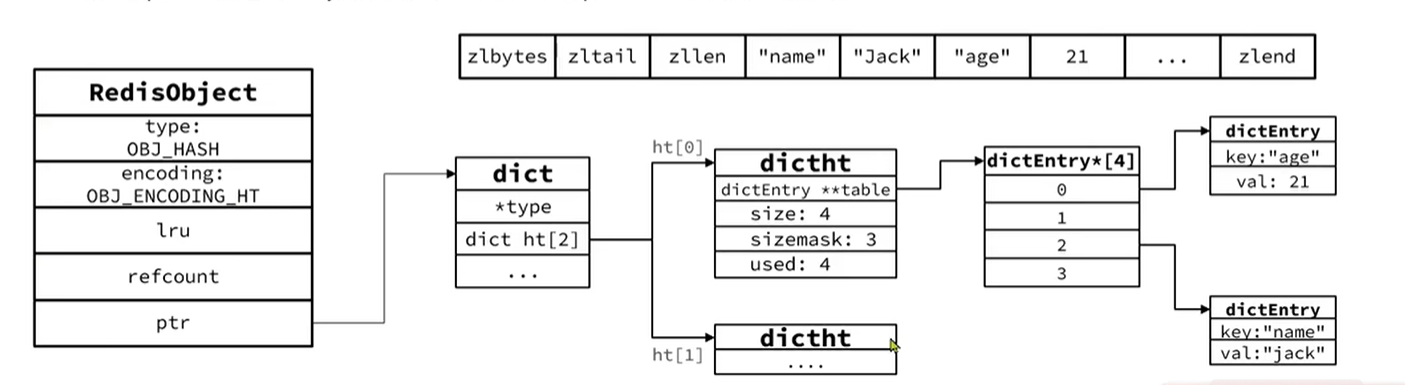
Redis原理篇——Redis数据结构
Redis原理篇 1、原理篇-Redis数据结构 1.1 Redis数据结构-动态字符串 我们都知道Redis中保存的Key是字符串,value往往是字符串或者字符串的集合。可见字符串是Redis中最常用的一种数据结构。 不过Redis没有直接使用C语言中的字符串,因为C语言字符串存…...

pdf文件预览和导出
抢先观看: window.URL.createObjectURL(): 用于根据传入的 Blob 对象或 File 对象生成一个临时的、可访问的 URL,仅在浏览器会话中有效,并且不会上传到服务器。 const url window.URL.createObjectURL(blob);Blob 对象: 是 …...

服务器数据恢复—RAID5阵列硬盘坏道掉线导致存储不可用的数据恢复案例
服务器存储数据恢复环境: 一台EqualLogic存储中有一组由16块SAS硬盘组建的RAID5阵列。上层划分了4个卷,采用VMFS文件系统,存放虚拟机文件。 服务器存储故障: 存储RAID5阵列中磁盘出现故障,有2块硬盘对应的指示灯亮黄灯…...

快速傅里叶变换(FFT)基础(附python实现)
对于非专业人士,傅里叶变换一直是一个神秘的武器,它可以分析出不同频域的信息,从时域转换到频域,揭示了信号的频率成分,对于数字信号处理(DSP)、图像、语音等数据来说,傅里叶变换是最…...

使用Docker-compose安装mysql5.7
1.首先选择一个目录用来存放docker-compse文件以及mysql的数据(例如logs、conf) cd /home mkdir mysql vi docker-compose.yml2.填写docker-compse.yml内容 version : 3 services:mysql:# 容器名(以后的控制都通过这个)container_name: mysql# 重启策略…...

如何管理PHP的API部署环境
管理PHP的API部署环境是一个涉及多个步骤和考虑因素的过程。以下是一些关键步骤和最佳实践,用于管理PHP的API部署环境: 一、选择合适的服务器和配置环境 选择服务器:根据API的访问量和性能需求,选择合适的服务器。可以选择物理服…...

web——sqliabs靶场——第一关
今天开始搞这个靶场,从小白开始一点点学习,加油!!!! 1.搭建靶场 注意点:1.php的版本问题,要用老版本 2.小p要先改数据库的密码,否则一直显示链接不上数据库 2.第一道题࿰…...

tartanvo ubuntu 20.04部署
1. 所有环境安装流程参考 2. 运行python3 tartanvo_node.py出现问题: ImportError: cannot import name int from numpy版本问题,卸载当前版本并更换版本: pip uninstall numpy pip install numpy1.22.4问题解决。 3. 采用2to3脚本将其代…...
)
SpringBoot整合Freemarker(三)
定义循环输出的宏 <#macro list title items> ${title?cap_first}:<#list items as x>*${x?cap_first}</#list> </#macro><list items["mouse", "elephant", "python"] title"Animals"/> 输出结果…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

Matlab实现任意伪彩色图像可视化显示
Matlab实现任意伪彩色图像可视化显示 1、灰度原始图像2、RGB彩色原始图像 在科研研究中,如何展示好看的实验结果图像非常重要!!! 1、灰度原始图像 灰度图像每个像素点只有一个数值,代表该点的亮度(或…...

用递归算法解锁「子集」问题 —— LeetCode 78题解析
文章目录 一、题目介绍二、递归思路详解:从决策树开始理解三、解法一:二叉决策树 DFS四、解法二:组合式回溯写法(推荐)五、解法对比 递归算法是编程中一种非常强大且常见的思想,它能够优雅地解决很多复杂的…...
