飞凌嵌入式FET527N-C核心板现已适配Android 13
飞凌嵌入式FET527N-C核心板现已成功适配Android13,新系统的支持能够为用户提供更优质的使用体验。那么,运行Android13系统的FET527N-C核心板具有哪些突出的优势呢?

1、性能与兼容性提升
飞凌嵌入式FET527N-C核心板搭载了全志T527系列高性能处理器,8个ARM Cortex-A55核心以及内置的RISC-V核和DSP核相互协作,共同提供了出色的处理能力和能效比。而Android13系统的适配,则进一步提升了核心板的兼容性。
2、应用生态丰富
Android13系统拥有庞大的应用生态支持,无论是娱乐软件、办公工具、工业产品还是其他领域的应用,几乎都能找到适合的应用开发组件。FET527N-C核心板适配Android13系统后,用户将能够享受到这些丰富多样的应用,满足多样化的需求。
3、流畅度与稳定性提升
经过深度优化和适配,Android13系统可以在FET527N-C核心板上更加流畅的运行应用,减少了卡顿和延迟现象。同时,Android13系统加强了安全性和隐私保护,为用户的数据安全提供了更加坚实的保障。
4、硬件加速特性
Android13系统支持更多的硬件加速特性,这使得FET527N-C核心板在图像处理、视频编码等方面表现出色。配合上FET527N-C核心板强大的性能和丰富的功能接口,能够带来更好的功能表现。
5、用户定制化体验
Android13系统的易用性和个性化设置功能,使得用户可以根据自己的需求进行定制,因此能够更好地为HMI赋能,不论是在工控、电力、交通还是医疗行业,都可以让机器更智能地作业,与人类更高效地交互。
6、国产化选料保障,稳定供应
此外,FET527N-C核心板在选料上实现了从内存到电源管理芯片再到每一颗阻容件的全面国产化,提升了产品的安全性和竞争力。同时,FET527N-C核心板具有10~15年生命周期,为您的产品提供持续供应保障。
总结来说,飞凌嵌入式FET527N-C核心板与Android13系统的结合,为嵌入式设备领域带来了新的发展机遇。这一结合不仅提升了核心板的性能和兼容性,也为用户提供了更为丰富和流畅的使用体验。未来,飞凌嵌入式将继续致力于技术创新和产品研发,为千行百业提供更多高质量的解决方案。
相关文章:

飞凌嵌入式FET527N-C核心板现已适配Android 13
飞凌嵌入式FET527N-C核心板现已成功适配Android13,新系统的支持能够为用户提供更优质的使用体验。那么,运行Android13系统的FET527N-C核心板具有哪些突出的优势呢? 1、性能与兼容性提升 飞凌嵌入式FET527N-C核心板搭载了全志T527系列高性能处…...
触发的返回事件)
uniapp 如何修改 返回按钮(左上角+物理按钮+侧滑)触发的返回事件
背景: 使用uniapp 开发安卓app,在用户编辑后直接返回时,使用弹窗提醒用户:还没有保存,是否保存? 方案 1. 使用自定义返回事件 //返回 back() { // 业务逻辑,弹窗提醒 uni.showModal({title:…...

appium启动 install driver安装驱动
appium启动 appiumPS C:\Windows\system32> appium [Appium] Welcome to Appium v2.12.1 [Appium] The autodetected Appium home path: C:\Users\liyd\.appium [HTTP] Could not start REST http interface listener. The requested port may already be in use. Please m…...
【机器学习】均方误差根(RMSE:Root Mean Squared Error)
均方误差根(Root Mean Squared Error,RMSE)是机器学习和统计学中常用的误差度量指标,用于评估预测值与真实值之间的差异。它通常用于回归模型的评价,以衡量模型的预测精度。 RMSE的定义与公式 给定预测值 和实际值 …...
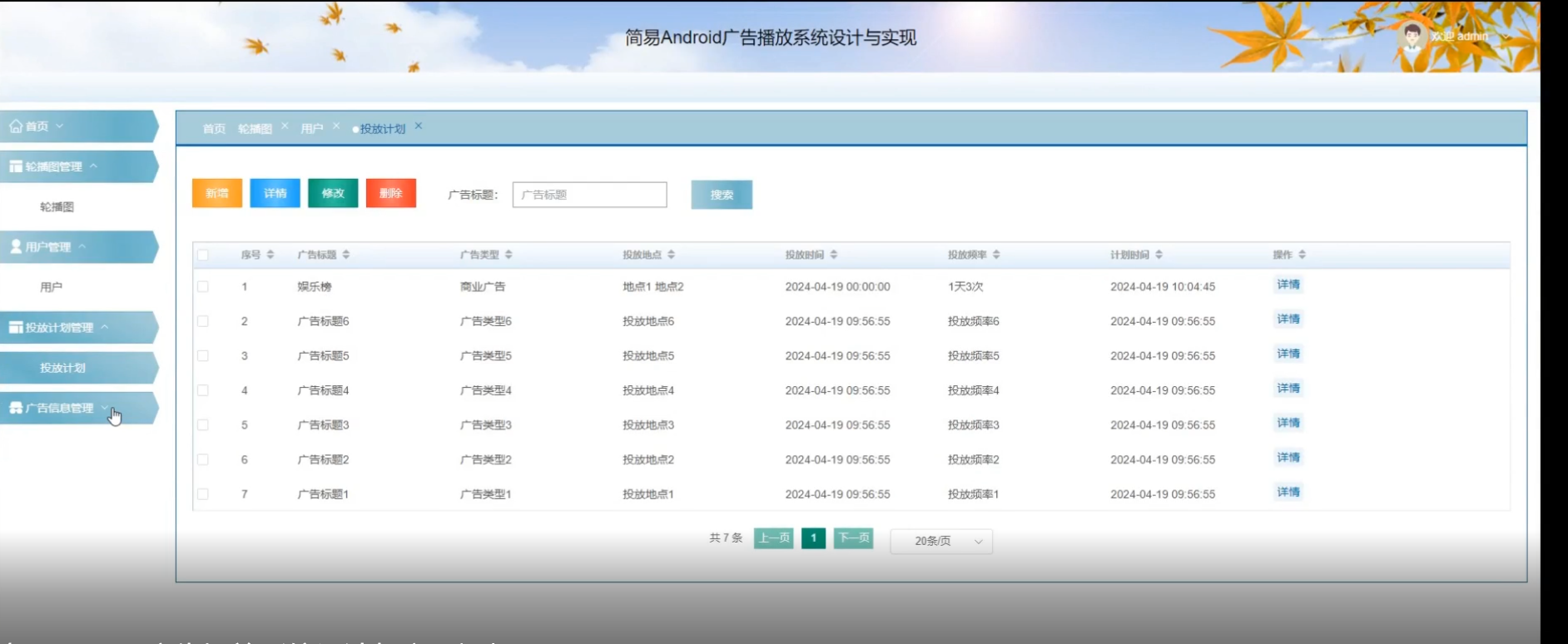
[含文档+PPT+源码等]精品基于springboot实现的原生Andriod广告播放系统
基于Spring Boot实现的原生Android广告播放系统背景,主要可以从以下几个方面进行阐述: 一、市场需求与背景 移动互联网的快速发展: 随着移动互联网技术的不断进步,智能手机已成为人们日常生活中不可或缺的一部分。人们越来越多地…...
【机器学习】均方误差(MSE:Mean Squared Error)
均方误差(Mean Squared Error, MSE)是衡量预测值与真实值之间差异的一种方法。在统计学和机器学习中,MSE 是一种常见的损失函数,用于评估模型的预测准确性。 均方误差的定义 假设有一组真实值 和模型预测的对应值 。均方误…...

融合虚拟与现实,AR Engine为用户提供沉浸式交互体验
当今的应用市场中,传统的应用产品已经难以完全满足消费者的多样化需求。为了在竞争激烈的市场中脱颖而出,企业需要深入洞察用户需求,提供个性化的服务体验和差异化的产品创新,以吸引并留住消费者。 比如,购物类App通过…...

python | xmltodict,一个非常厉害的 关于XML数据 Python 库!
本文来源公众号“python”,仅用于学术分享,侵权删,干货满满。 原文链接:xmltodict,一个非常厉害的 Python 库! 大家好,今天为大家分享一个非常厉害的 Python 库 - xmltodict。 Github地址&am…...
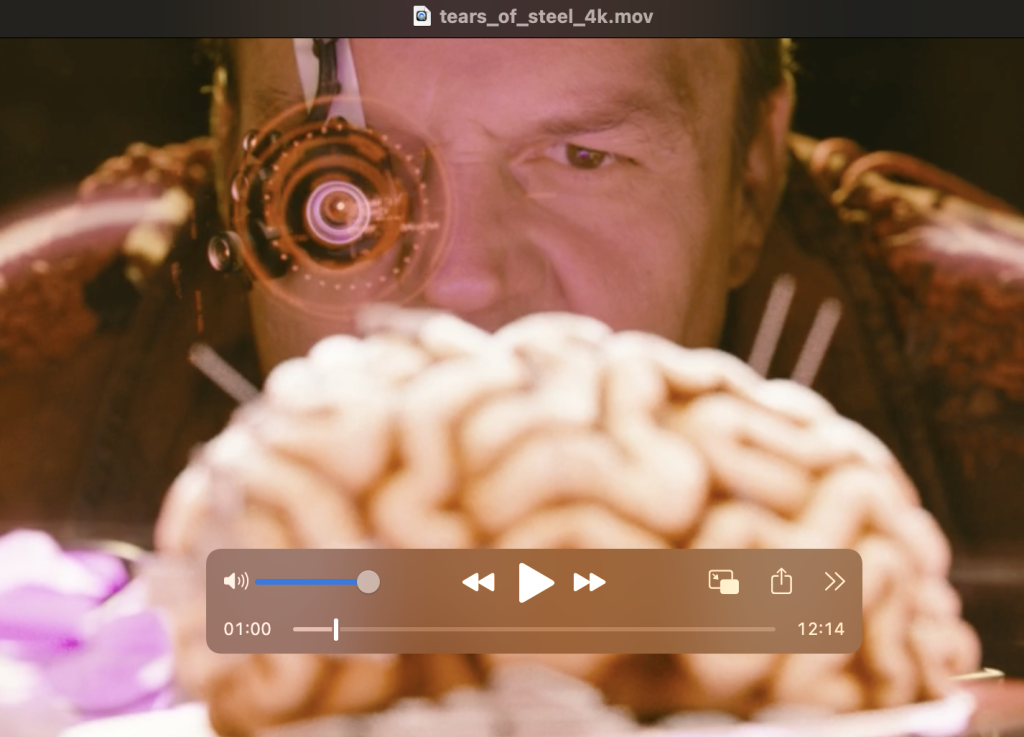
教程:FFmpeg结合GPU实现720p至4K视频转换
将一个 720p 的视频放大编码到 4K,这样的视频处理在很多业务场景中都会用到。很多视频社交、短视频、视频点播等应用,都会需要通过服务器来处理大量的视频编辑需求。 本文我们会探讨一下做这样的视频处理,最低的 GPU 指标应该是多少。利用开源…...

MeterSphere接口自动化-ForEach循环
接口自动化场景:一个接口根据不同的参数取值来运行测试,本场景中只有一个参数来去不同值。举例如下: https:://test.csdn/query?placementList1接口,测试id1,2,3时,断言接口返回的data数据都有返回。(当然…...

ssm074应急资源管理系统+jsp(论文+源码)_kaic
毕 业 设 计(论 文) 题目:应急资源管理系统设计与实现 摘 要 现代经济快节奏发展以及不断完善升级的信息化技术,让传统数据信息的管理升级为软件存储,归纳,集中处理数据信息的管理方式。本应急资源管理系统…...
怎么对 PDF 添加权限密码或者修改密码-免费软件分享
序言 目前市面上有关PDF处理的工具有很多,不过绝大多数的PDF处理工具都需要付费使用,且很多厂商甚至连试用的机会也不给用户,偶有试用的,其试用版的条件也极为苛刻,比如只能处理前两页,或者只能处理非常小的…...

LVSM: A LARGE VIEW SYNTHESIS MODEL WITH MINIMAL 3D INDUCTIVE BIAS 论文解读
目录 一、概述 二、相关工作 1、新视角合成 2、优化3D表示 3、可泛化的前馈方法 三、LVSM 1、总体结构 2、encoder-decoder 3、decoder-only 4、Loss 一、概述 该论文提出大视角合成模型LVSM,基于Transformer方法,用于场景中或对象级层次从稀…...

7.《双指针篇》---⑦三数之和(中等偏难)
题目传送门 方法一:双指针 1.新建一个顺序表用来返回结果。并排序数组。 2.for循环 i 从第一个数组元素遍历到倒数第三个数。 3.如果遍历过程中有值大于0的则break; 4.定义左右指针,以及target。int left i 1, right n - 1; int target -nums[i];…...

鸿蒙ArkTS中的布局容器组件(Scroll、List、Tabs)
1、Scroll组件 Scroll组件是一个可滚动的容器组件,用于在子组件的布局尺寸超过父组件尺寸时提供滚动功能。它允许在其内部容纳超过自身显示区域的内容,并通过滚动机制来查看全部内容。这对于显示大量信息(如长列表、长篇文本或大型图像等&…...

mybatis连接PGSQL中对于json和jsonb的处理
pgsql数据库表字段设置了jsonb格式;在java的实体里使用String或者对象转换会一直提示一个错误: Caused by: org.postgresql.util.PSQLException: ERROR: column "xx" is of type jsonb but expression is of type character varying 需要加一…...

Redis 权限控制(ACL)|ACL 命令详解、ACL 持久化
官网文档地址:https://redis.io/docs/latest/operate/oss_and_stack/management/security/acl/ 使用版本:Redis7.4.1 什么是 ACL? ACL(Access Control List),权限控制列表,是 Redis 提供的一种…...

内网学习一:windows基础
工作组介绍 按照不同的计算机功能或工作部门将计算机列入不同的工作组。要是想访问某一个工作组的资源 只需要双击该部门的工作组,就可以看到该组内的所有计算机。 目的:在大型网络中,方便管理员去管理设备 加入工作组 右击计算机图标---…...

编译工具与文件学习(一)-YAML、repos、vcstoolcolcon
YAML YAML(YAML Ain’t Markup Language)是一种人类可读的数据序列化格式,常用于配置文件、数据交换和存储结构化数据。YAML 的设计目标是简洁、易读,并且能够表示复杂的数据结构。 YAML 文件的基本语法 基本结构: Y…...

使用 HuggingFace 提供的 Elasticsearch 托管交叉编码器进行重新排名
作者:来自 Elastic Jeff Vestal 了解如何使用 Hugging Face 的模型在 Elasticsearch 中托管和执行语义重新排序。 在这篇简短的博文中,我将向你展示如何使用 Hugging Face 中的模型在搜索时在你自己的 Elasticsearch 集群中执行语义重新排序。我们将使用…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...

AWS vs 阿里云:功能、服务与性能对比指南
在云计算领域,Amazon Web Services (AWS) 和阿里云 (Alibaba Cloud) 是全球领先的提供商,各自在功能范围、服务生态系统、性能表现和适用场景上具有独特优势。基于提供的引用[1]-[5],我将从功能、服务和性能三个方面进行结构化对比分析&#…...
