用 Python 从零开始创建神经网络(五):损失函数(Loss Functions)计算网络误差
用损失函数(Loss Functions)计算网络误差
- 引言
- 1. 分类交叉熵损失(Categorical Cross-Entropy Loss)
- 2. 分类交叉熵损失类(The Categorical Cross-Entropy Loss Class)
- 展示到目前为止的所有代码
- 3. 准确率计算(Accuracy Calculation)
引言

在随机初始化的模型中,或者即使是采用更复杂方法初始化的模型中,我们的目标是随着时间的推移培训或教育一个模型。为了训练一个模型,我们调整权重和偏差以提高模型的准确性和置信度。为此,我们需要计算模型的错误量。损失函数,也被称为成本函数,是量化模型错误程度的算法。损失是这一指标的衡量。由于损失是模型的错误,我们理想情况下希望它为0。
你可能会想知道为什么我们不根据 argmax 准确度来计算模型的错误。回想我们之前的置信度示例:[0.22, 0.6, 0.18] 对比 [0.32, 0.36, 0.32]。如果正确的类确实是中间的那一个(索引1),那么两个例子之间的模型准确性将是相同的。但是这两个例子真的像彼此那样准确吗?它们不是,因为准确性只是简单地应用一个 argmax 到输出上,以找到最大值的索引。神经网络的输出实际上是置信度,对正确答案的更多置信度是更好的。因此,我们努力增加正确的置信度并减少错误放置的置信度。
1. 分类交叉熵损失(Categorical Cross-Entropy Loss)
如果你熟悉线性回归,那么你已经知道了用于神经网络进行回归的一个损失函数:平方误差(或神经网络中的均方误差)。
在这个例子中,我们不是在进行回归,我们是在进行分类,所以我们需要一个不同的损失函数。模型的输出层使用softmax激活函数,这意味着它输出一个概率分布。分类交叉熵专门用于比较一个“真实”概率( y y y 或“目标”)和某个预测分布( y − h a t y-hat y−hat 或“预测”),因此在这里使用交叉熵是有意义的。它也是输出层上使用softmax激活时最常用的损失函数之一。
计算 y y y (实际/期望分布)和 y − h a t y-hat y−hat 帽(预测分布)的分类交叉熵的公式是:

其中 L i L_i Li 表示样本的损失值, i i i 是集合中的第 i i i 个样本, j j j 是标签/输出索引, y y y 表示目标值,而 y ^ \hat{y} y^ 表示预测值。
一旦我们开始编写解决方案,我们会进一步简化它为 − log ( c o r r e c t _ c l a s s _ c o n f i d e n c e ) -\log({correct\_class\_confidence}) −log(correct_class_confidence),其公式为:

其中 L i L_i Li 表示样本的损失值, i i i 是数据集中第 i i i 个样本, k k k 是目标标签的索引(真实标签), y y y 表示目标值, y ^ \hat{y} y^ 表示预测值。
你可能会问,为什么我们称这为交叉熵而不是对数损失,后者也是一种损失类型。如果你不知道什么是对数损失,你可能会想知道为什么这样一个看似非常基本的描述会有这样一个看似复杂的公式。
通常情况下,对数损失误差函数是我们应用于二元逻辑回归模型输出的函数(我们将在第十六章描述)——分布中只有两个类别,每个类别对应一个单一输出(神经元),该输出被标记为0或1。在我们的案例中,我们有一个分类模型,它返回所有输出的概率分布。交叉熵比较两个概率分布。在我们的案例中,我们有一个softmax输出,比如说是:
softmax_output = [0.7, 0.1, 0.2]
我们打算将这个概率分布与哪一个进行比较?在上述输出中,我们有3个类的置信度,假设期望的预测是第一类(索引0,当前为0.7)。如果这是预期的预测,那么期望的概率分布是 [1, 0, 0]。交叉熵也可以应用于像 [0.2, 0.5, 0.3] 这样的概率分布;它们不必看起来像上面那样。也就是说,期望的概率将包括在期望类别中为1,在其余不期望的类别中为0。这样的数组或向量被称为one-hot,意味着其中一个值是“热”(开),值为1,其余的是“冷”(关),值为0。当使用交叉熵将模型的结果与one-hot向量进行比较时,方程的其他部分将归零,目标概率的对数损失乘以1,使得交叉熵计算相对简单。这也是交叉熵计算的一个特殊情况,称为分类交叉熵。举个例子 — 如果我们取一个softmax输出 [0.7, 0.1, 0.2] 和目标 [1, 0, 0],我们可以按以下方式进行计算:

如果还是不理解的话,我的理解是背下来就好。你只需要知道的事情是,我们需要一个Loss函数来更新神经网络使得 y y y和 y ^ \hat{y} y^尽可能接近。至于使用哪个Loss函数,或者Loss函数是什么样的,直接上网查就行。
让我们看看相关的 Python 代码:
import math# An example output from the output layer of the neural network
softmax_output = [0.7, 0.1, 0.2]# Ground truth
target_output = [1, 0, 0]loss = -(math.log(softmax_output[0])*target_output[0] +math.log(softmax_output[1])*target_output[1] +math.log(softmax_output[2])*target_output[2])print(loss)
>>>
0.35667494393873245
这就是完整的分类交叉熵计算,但鉴于one-hot目标向量,我们可以做一些假设。首先,这种情况下 target_output[1] 和 target_output[2] 的值是多少?它们都是0,任何数乘以0都是0。因此,我们不需要计算这些索引。接下来,这种情况下 target_output[0] 的值是多少?它是1。所以这也可以省略,因为任何数乘以1仍然是相同的。那么,在这个例子中,相同的输出可以用以下方式计算:
import math# An example output from the output layer of the neural network
softmax_output = [0.7, 0.1, 0.2]loss = -math.log(softmax_output[0])print(loss)
>>>
0.35667494393873245
正如你可以看到的,对于代表目标的one-hot向量或标量值,我们可以做一些简单的假设并使用更基本的计算方法——曾经涉及的公式简化为目标类别置信度得分的负对数——这是本章开头介绍的第二个公式。
正如我们已经讨论过的,示例置信水平可能看起来像 [0.22, 0.6, 0.18] 或 [0.32, 0.36, 0.32]。在这两种情况下,这些向量的 argmax 都会返回第二个类别作为预测,但模型对这些预测的置信度只对其中一个是高的。分类交叉熵损失考虑到这一点,并且输出的损失值会随着置信度的降低而增大:
import mathprint(math.log(1.))
print(math.log(0.95))
print(math.log(0.9))
print(math.log(0.8))
print('...')
print(math.log(0.2))
print(math.log(0.1))
print(math.log(0.05))
print(math.log(0.01))
>>>
0.0
-0.05129329438755058
-0.10536051565782628
-0.2231435513142097
...
-1.6094379124341003
-2.3025850929940455
-2.995732273553991
-4.605170185988091
我们为一些示例置信度打印了不同的对数值。当置信水平等于1,意味着模型对其预测100%“确定”时,这个样本的损失值等于0。随着置信水平的提高,损失值趋近于0。你可能还会想知道为什么我们没有打印 log(0) 的结果——我们将很快解释这一点。
到目前为止,我们已经将 log() 应用于 softmax 输出,但还没有解释“log”是什么,以及为什么使用它。我们将在下一章讨论“为什么”,那一章将涵盖导数、梯度和优化;可以说,log 函数具有一些理想的属性。Log 是对数(logarithm)的简称,被定义为方程 a x = b a^x = b ax=b 中 x x x 项的解。例如, 1 0 x = 100 10^x = 100 10x=100 可以用对数解决: log 10 ( 100 ) \log_{10}(100) log10(100),结果为2。当基数使用 e e e(欧拉数或约2.71828)时,log 函数的这个属性尤其有利(在示例中基数为10)。以 e e e 为基数的对数称为自然对数,简称自然 log 或 log ——你也可能看到这样写: ln ( x ) = log ( x ) = log e ( x ) \ln(x) = \log(x) = \log_e(x) ln(x)=log(x)=loge(x)。各种约定可能会使这变得混乱,因此为了简化事物,提到的任何 log 都将始终是自然对数。自然对数表示方程 e x = b e^x = b ex=b 中 x x x 项的解;例如, e x = 5.2 e^x = 5.2 ex=5.2 由 log ( 5.2 ) \log(5.2) log(5.2) 解决。
在 Python 代码中:
import numpy as npb = 5.2print(np.log(b))
>>>
1.6486586255873816
我们可以通过对结果进行指数化来证实这一点:
import mathprint(math.e ** 1.6486586255873816)
>>>
5.199999999999999
这种微小的差异是由于 Python 中浮点数精度引起的。回到损失计算,我们需要以两种额外的方式修改我们的输出。首先,我们将更新我们的过程,使其能够处理批量的 softmax 输出分布;其次,使负对数计算动态对应到目标索引(目标索引到目前为止已经被硬编码)。
考虑一个场景,神经网络在三个类别之间进行分类,并且神经网络以三批的方式进行分类。在通过 softmax 激活函数处理一批3个样本和3个类别之后,网络的输出层产生如下:
# Probabilities for 3 samples
softmax_outputs = np.array([[0.7, 0.1, 0.2],[0.1, 0.5, 0.4],[0.02, 0.9, 0.08]])
我们需要一种动态计算分类交叉熵的方法,现在我们知道这是一个负对数计算。要确定从 softmax 输出中计算负对数的哪个值,我们只需要知道我们的目标值。在这个例子中,有3个类别;假设我们试图将某物分类为“狗”、“猫”或“人”。狗是第0类(索引0),猫是第1类(索引1),人是第2类(索引2)。假设这批三个样本输入到这个神经网络被映射到一只狗、一只猫和一只猫的目标值。所以目标(作为目标索引列表)将是 [0, 1, 1]。
softmax_outputs = [[0.7, 0.1, 0.2],[0.1, 0.5, 0.4],[0.02, 0.9, 0.08]]class_targets = [0, 1, 1] # dog, cat, cat
类别目标中的第一个值0意味着第一个softmax输出分布的预期预测是 [0.7, 0.1, 0.2] 中索引0处的值;模型对这个观察是狗有0.7的置信度。这种情况在整个批次中持续,第二个softmax分布 [0.1, 0.5, 0.4] 的预期目标在索引1处;模型对这是一只猫只有0.5的置信度——模型对这个观察不太确定。在最后一个样本中,它也是来自softmax分布的第二个索引,在这种情况下是0.9的值——相当高的置信度。
有了一系列softmax输出及其预期目标,我们可以映射这些索引以从softmax分布中检索值:
softmax_outputs = [[0.7, 0.1, 0.2],[0.1, 0.5, 0.4],[0.02, 0.9, 0.08]]class_targets = [0, 1, 1]for targ_idx, distribution in zip(class_targets, softmax_outputs):print(targ_idx, distribution)print(distribution[targ_idx])print("====================")
>>>
0 [0.7, 0.1, 0.2]
0.7
====================
1 [0.1, 0.5, 0.4]
0.5
====================
1 [0.02, 0.9, 0.08]
0.9
====================
同样,zip() 函数可以让我们在 Python 中同时遍历多个迭代表。使用 NumPy 可以进一步简化这一过程(这次我们将创建一个包含 Softmax 输出的 NumPy 数组):
import numpy as npsoftmax_outputs = np.array([[0.7, 0.1, 0.2],[0.1, 0.5, 0.4],[0.02, 0.9, 0.08]])class_targets = [0, 1, 1]
class_targets_value = softmax_outputs[[0, 1, 2], class_targets]print(class_targets_value)
>>>
[0.7 0.5 0.9]
0、1 和 2 这些值是什么意思?NumPy 允许我们以多种方式索引数组。其中一种方式是使用一个填充了索引的列表,这对我们来说很方便——我们可以使用 class_targets 来实现这一目的,因为它已经包含了我们感兴趣的索引列表。问题是这必须过滤数组中的数据行——第二维。为了执行这一操作,我们还需要明确地在其第一维过滤这个数组。这一维包含预测,我们当然希望保留它们全部。我们可以通过使用一个包含从0到所有索引的数字的列表来实现这一点。我们知道我们将有和我们整个批次中的分布一样多的索引,所以我们可以使用 range() 而不是自己输入每个值:
import numpy as npsoftmax_outputs = np.array([[0.7, 0.1, 0.2],[0.1, 0.5, 0.4],[0.02, 0.9, 0.08]])class_targets = [0, 1, 1]
class_targets_value = softmax_outputs[range(len(softmax_outputs)), class_targets]print(class_targets_value )
>>>
[0.7 0.5 0.9]
这会返回每个样本在目标指数处的信度列表。现在我们对该列表应用负对数:
import numpy as npsoftmax_outputs = np.array([[0.7, 0.1, 0.2],[0.1, 0.5, 0.4],[0.02, 0.9, 0.08]])class_targets = [0, 1, 1]
neg_log= -np.log(softmax_outputs[range(len(softmax_outputs)), class_targets])print(neg_log)
>>>
[0.35667494 0.69314718 0.10536052]
最后,我们想要得到每批的平均损失值,以便了解我们的模型在训练期间的表现。在Python中有许多计算平均值的方法;最基本的平均值形式是算术平均值: s u m ( i t e r a b l e ) / l e n ( i t e r a b l e ) sum(iterable) / len(iterable) sum(iterable)/len(iterable)。NumPy有一个方法可以在数组上计算这个平均值,所以我们将使用它。我们在代码中添加NumPy的平均计算:
import numpy as npsoftmax_outputs = np.array([[0.7, 0.1, 0.2],[0.1, 0.5, 0.4],[0.02, 0.9, 0.08]])class_targets = [0, 1, 1]neg_log = -np.log(softmax_outputs[range(len(softmax_outputs)), class_targets])
average_loss = np.mean(neg_log)print(average_loss)>>>
0.38506088005216804
我们已经了解到目标可以进行一位有效编码(one-hot encoding),其中除了一个值是1,其余都是0,并且正确标签的位置填充为1。它们也可以是稀疏的,这意味着它们包含的数字是正确的类别编号——我们通过 spiral_data() 函数以这种方式生成它们,并且我们可以允许损失计算接受任何这些形式。
由于我们实现了这一点以适用于稀疏标签(如我们的训练数据),如果它们是一位有效编码,我们必须进行检查并在这种新情况下以不同方式处理。可以通过计数维度来执行检查——如果目标是单维的(如列表),它们是稀疏的;但如果有两个维度(如列表的列表),则是一组一位有效编码的向量。在这第二种情况下,我们将使用本章的第一个方程实现一个解决方案,而不是过滤目标标签处的置信度。我们必须将置信度与目标相乘,除了正确标签处的值外,将所有值归零,并沿行轴(轴1)进行求和。我们必须在刚刚编写的代码中添加一个对维数的测试,将对数值的计算移到这个新的 if 语句之外,并按照第一个方程实现一位有效编码标签的解决方案:
import numpy as npsoftmax_outputs = np.array([[0.7, 0.1, 0.2],[0.1, 0.5, 0.4],[0.02, 0.9, 0.08]])class_targets = np.array([[1, 0, 0],[0, 1, 0],[0, 1, 0]])
# class_targets = np.array([0, 1, 1])# Probabilities for target values -
# only if categorical labels
if len(class_targets.shape) == 1:correct_confidences = softmax_outputs[range(len(softmax_outputs)), class_targets]
# Mask values - only for one-hot encoded labels
elif len(class_targets.shape) == 2:correct_confidences = np.sum(softmax_outputs * class_targets,axis=1)# Losses
neg_log = -np.log(correct_confidences)average_loss = np.mean(neg_log)print(average_loss)
>>>
0.38506088005216804
在NumPy中,
axis参数定义了数组沿哪个维度进行操作。多维数组中,axis的值决定了函数是如何处理数组元素的:
axis=0:沿着第一个轴(“纵向”,“列方向”,“深度方向”),即将操作应用于跨行的同一列的所有元素axis=1:沿着第二个轴(“横向”,“行方向”),即将操作应用于同一行的所有元素axis=2:如果有的话,这通常是沿着第三维度(例如,在三维数组中),即针对每个"页"或"深度层"的同一位置的元素。
在Python的NumPy库中,当你使用
*操作符对两个数组进行运算时,它执行的是元素级别的乘法(也称为Hadamard乘积或点乘)。这意味着两个数组的相应元素相乘,结果数组的每个位置 i , j i, j i,j 是原来两个数组在该位置的元素相乘的结果。
- 第一行:
[0.7 × 1, 0.1 × 0, 0.2 × 0] = [0.7, 0, 0]- 第二行:
[0.1 × 0, 0.5 × 1, 0.4 × 0] = [0, 0.5, 0]- 第三行:
[0.02 × 0, 0.9 × 1, 0.08 × 0] = [0, 0.9, 0][[0.7, 0, 0],[0, 0.5, 0],[0, 0.9, 0]]
在我们继续之前,还有一个问题需要解决。Softmax 输出,也是这个损失函数的输入,由0到1范围内的数字组成——一系列置信度。模型可能会对某个标签有完全的信心,使得所有剩余的置信度为零。同样,模型也可能将完全的信心分配给一个非目标值。如果我们尝试计算这个置信度为0的损失:
import numpy as np-np.log(0)
>>>
163: RuntimeWarning: divide by zero encountered in log-np.log(0)
在我们解释这个问题之前,我们需要讨论一下 log ( 0 ) \log(0) log(0)。从数学的角度看, log ( 0 ) \log(0) log(0) 是未定义的。我们已经知道以下的依赖关系:如果 y = log ( x ) y = \log(x) y=log(x),那么 e y = x e^y = x ey=x。在 y = log ( 0 ) y = \log(0) y=log(0) 中所得到的 y y y 是什么,与在 e y = 0 e^y = 0 ey=0 中的 y y y 是什么一样。简单来说,常数 e e e 的任何幂都是一个正数,并且没有任何 y y y 可以使 e y = 0 e^y = 0 ey=0。这意味着 log ( 0 ) \log(0) log(0) 是未定义的。我们需要知道 log ( 0 ) \log(0) log(0) 是什么,而“未定义”并不意味着我们对它一无所知。既然 log ( 0 ) \log(0) log(0) 是未定义的,那么接近0的值的结果是什么呢?我们可以计算函数的极限。如何精确计算超出了本书的范围,但解决方案是:

我们将其读作自然对数 log ( x ) \log(x) log(x) 的极限,其中 x x x 从正值接近0(计算负值的自然对数是不可能的),等于负无穷。这意味着,对于无限小的 x x x,其极限是负无穷,其中 x x x 永远不会达到0。
在编程语言中情况略有不同。这里没有极限,只有一个函数,给定一个参数,返回某个值。在Python中使用NumPy,0的负自然对数等于一个无限大的数,而不是未定义,并且会打印一个关于0除错误的警告(这是这种计算方式的结果)。如果 − log ( 0 ) -\log(0) −log(0) 等于无穷大,用Python计算负无穷大的 e e e 次幂可能吗?
import numpy as npresult = np.e**(-np.inf)print(result)
>>>
0.0
在编程中,未定义的事物越少越好。稍后,我们将看到类似的简化,例如计算绝对值函数的导数,该导数在输入为0时不存在,我们将不得不做出一些决策来解决这个问题。
回到 − log ( 0 ) -\log(0) −log(0) 结果为无穷大的情况——尽管这在数学上是有意义的,因为模型完全错误,但这将为我们进一步进行计算带来问题。稍后,在进行优化时,我们还会在计算梯度时遇到问题,从所有样本损失的平均值开始,因为列表中单个无穷大的值会导致该列表的平均值也是无穷大:
import numpy as npresult = np.mean([1, 2, 3, -np.log(0)])print(result)
>>>
177: RuntimeWarning: divide by zero encountered in logresult = np.mean([1, 2, 3, -np.log(0)])
我们可以为置信度添加一个很小的值,以防止它为零,例如1e-7:
import numpy as npresult = -np.log(1e-7)print(result)
>>>
16.11809565095832
在置信度的最边缘添加一个很小的值,即十万分之一,对结果的影响微乎其微,但这种方法会产生另外两个问题。首先,在置信度值为1 :
import numpy as npresult = -np.log(1+1e-7)print(result)
>>>
-9.999999505838704e-08
当模型在预测中完全正确,并将所有置信度放在正确的标签上时,损失会变成负值,而不是0。这里的另一个问题是置信度向1移动,即使是非常小的值。为了防止这两个问题,最好从两端同时剪切值,我们的案例中是1e-7。这意味着可能的最低值将变为1e-7(就像我们刚才演示的那样),但可能的最高值,而不是1+1e-7,将变为1-1e-7(稍微低于1):
import numpy as npresult = -np.log(1-1e-7)print(result)
>>>
1.0000000494736474e-07
这将使损失不会正好为0,而是一个非常小的值,但不会使其成为负值,也不会使整体损失偏向1。 在我们的代码中,使用 numpy,我们将使用 np.clip() 方法来实现这一点:
import numpy as npy_pred = np.array([0.1, 0.2, 0.3, np.inf, -np.inf])y_pred_clipped = np.clip(y_pred, 1e-7, 1-1e-7)print(y_pred_clipped)
>>>
[1.000000e-01 2.000000e-01 3.000000e-01 9.999999e-01 1.000000e-07]
该方法可以对数值数组执行剪切,因此我们可以直接将其应用于预测值,并将其保存为一个单独的数组,稍后我们将使用该数组。
2. 分类交叉熵损失类(The Categorical Cross-Entropy Loss Class)
在后续章节中,我们将添加更多的损失函数,我们将执行的一些操作对所有这些损失函数都是通用的。其中一个操作是我们如何计算总损失——无论我们使用哪种损失函数,总损失始终是所有样本损失的平均值。让我们创建一个包含 calculate 方法的 Loss 类,该方法将调用我们的损失对象的 forward 方法,并计算返回的样本损失的平均值:
import numpy as np# Common loss class
class Loss:# Calculates the data and regularization losses# given model output and ground truth valuesdef calculate(self, output, y):# Calculate sample lossessample_losses = self.forward(output, y)# Calculate mean lossdata_loss = np.mean(sample_losses)# Return lossreturn data_loss
在后面的章节中,我们将为该类添加更多代码,它存在的理由也将变得更加清晰。现在,我们只需使用它这一个目的。
让我们把损失代码转换成一个类,以方便下一步操作:
# Cross-entropy loss
class Loss_CategoricalCrossentropy(Loss):# Forward passdef forward(self, y_pred, y_true):# Number of samples in a batchsamples = len(y_pred)# Clip data to prevent division by 0# Clip both sides to not drag mean towards any valuey_pred_clipped = np.clip(y_pred, 1e-7, 1 - 1e-7)# Probabilities for target values -# only if categorical labelsif len(y_true.shape) == 1:correct_confidences = y_pred_clipped[range(samples), y_true]# Mask values - only for one-hot encoded labelselif len(y_true.shape) == 2:correct_confidences = np.sum(y_pred_clipped * y_true, axis=1)# Lossesnegative_log_likelihoods = -np.log(correct_confidences)return negative_log_likelihoods
该类继承于 Loss 类,可执行本章衍生的所有误差计算,并可作为对象使用。例如,使用手动创建的输出和目标:
import numpy as np# Common loss class
class Loss:# Calculates the data and regularization losses# given model output and ground truth valuesdef calculate(self, output, y):# Calculate sample lossessample_losses = self.forward(output, y)# Calculate mean lossdata_loss = np.mean(sample_losses)# Return lossreturn data_loss# Cross-entropy loss
class Loss_CategoricalCrossentropy(Loss):# Forward passdef forward(self, y_pred, y_true):# Number of samples in a batchsamples = len(y_pred)# Clip data to prevent division by 0# Clip both sides to not drag mean towards any valuey_pred_clipped = np.clip(y_pred, 1e-7, 1 - 1e-7)# Probabilities for target values -# only if categorical labelsif len(y_true.shape) == 1:correct_confidences = y_pred_clipped[range(samples), y_true]# Mask values - only for one-hot encoded labelselif len(y_true.shape) == 2:correct_confidences = np.sum(y_pred_clipped * y_true, axis=1)# Lossesnegative_log_likelihoods = -np.log(correct_confidences)return negative_log_likelihoodssoftmax_outputs = np.array([[0.7, 0.1, 0.2],[0.1, 0.5, 0.4],[0.02, 0.9, 0.08]])class_targets = np.array([0, 1, 1])
# class_targets = np.array([[1, 0, 0],
# [0, 1, 0],
# [0, 1, 0]])loss_function = Loss_CategoricalCrossentropy()
loss = loss_function.calculate(softmax_outputs, class_targets)print(loss)
展示到目前为止的所有代码
import numpy as np
import nnfs
from nnfs.datasets import spiral_datannfs.init()# Dense layer
class Layer_Dense:# Layer initializationdef __init__(self, n_inputs, n_neurons):# Initialize weights and biasesself.weights = 0.01 * np.random.randn(n_inputs, n_neurons)self.biases = np.zeros((1, n_neurons))# Forward passdef forward(self, inputs):# Calculate output values from inputs, weights and biasesself.output = np.dot(inputs, self.weights) + self.biases# ReLU activation
class Activation_ReLU:# Forward passdef forward(self, inputs):# Calculate output values from inputself.output = np.maximum(0, inputs)# Softmax activation
class Activation_Softmax:# Forward passdef forward(self, inputs):# Get unnormalized probabilitiesexp_values = np.exp(inputs - np.max(inputs, axis=1, keepdims=True))# Normalize them for each sampleprobabilities = exp_values / np.sum(exp_values, axis=1, keepdims=True)self.output = probabilities# Common loss class
class Loss:# Calculates the data and regularization losses# given model output and ground truth valuesdef calculate(self, output, y):# Calculate sample lossessample_losses = self.forward(output, y)# Calculate mean lossdata_loss = np.mean(sample_losses)# Return lossreturn data_loss# Cross-entropy loss
class Loss_CategoricalCrossentropy(Loss):# Forward passdef forward(self, y_pred, y_true):# Number of samples in a batchsamples = len(y_pred)# Clip data to prevent division by 0# Clip both sides to not drag mean towards any valuey_pred_clipped = np.clip(y_pred, 1e-7, 1 - 1e-7)# Probabilities for target values -# only if categorical labelsif len(y_true.shape) == 1:correct_confidences = y_pred_clipped[range(samples), y_true]# Mask values - only for one-hot encoded labelselif len(y_true.shape) == 2:correct_confidences = np.sum(y_pred_clipped * y_true, axis=1)# Lossesnegative_log_likelihoods = -np.log(correct_confidences)return negative_log_likelihoods# Create dataset
X, y = spiral_data(samples=100, classes=3)# Create Dense layer with 2 input features and 3 output values
dense1 = Layer_Dense(2, 3)# Create ReLU activation (to be used with Dense layer):
activation1 = Activation_ReLU()# Create second Dense layer with 3 input features (as we take output
# of previous layer here) and 3 output values
dense2 = Layer_Dense(3, 3)# Create Softmax activation (to be used with Dense layer):
activation2 = Activation_Softmax()# Create loss function
loss_function = Loss_CategoricalCrossentropy()# Make a forward pass of our training data through this layer
dense1.forward(X)# Make a forward pass through activation function
# it takes the output of first dense layer here
activation1.forward(dense1.output)# Make a forward pass through second Dense layer
# it takes outputs of activation function of first layer as inputs
dense2.forward(activation1.output)# Make a forward pass through activation function
# it takes the output of second dense layer here
activation2.forward(dense2.output)# Let's see output of the first few samples:
print(activation2.output[:5])# Perform a forward pass through loss function
# it takes the output of second dense layer here and returns loss
loss = loss_function.calculate(activation2.output, y) # Print loss value
print('loss:', loss)
>>>
[[0.33333334 0.33333334 0.33333334][0.3333332 0.3333332 0.33333364][0.3333329 0.33333293 0.3333342 ][0.3333326 0.33333263 0.33333477][0.33333233 0.3333324 0.33333528]]
loss: 1.0986104
3. 准确率计算(Accuracy Calculation)
尽管损失是优化模型的一个有用指标,但在实践中常用的与损失一起使用的指标是准确率,它描述了最大置信度是正确类别的频率,以分数形式表示。方便地,我们可以重用现有的变量定义来计算准确率指标。我们将使用 softmax 输出的 argmax 值,然后将这些值与目标进行比较。这就像做以下操作一样简单(注意我们稍微修改了 softmax_outputs 以适应这个例子):
import numpy as np# Probabilities of 3 samples
softmax_outputs = np.array([[0.7, 0.2, 0.1],[0.5, 0.1, 0.4],[0.02, 0.9, 0.08]])
# Target (ground-truth) labels for 3 samples
class_targets = np.array([0, 1, 1])
# class_targets = np.array([[1, 0, 0], # one-hot encoded
# [0, 1, 0],
# [0, 1, 0]])
print("class_targets:", class_targets)# Calculate values along second axis (axis of index 1)
predictions = np.argmax(softmax_outputs, axis=1)
print("predictions:", predictions)# If targets are one-hot encoded - convert them
if len(class_targets.shape) == 2:class_targets = np.argmax(class_targets, axis=1)print("class_targets:", class_targets)# True evaluates to 1; False to 0
accuracy = np.mean(predictions==class_targets)print('acc:', accuracy)
>>>
class_targets: [0 1 1]
predictions: [0 0 1]
acc: 0.6666666666666666
我们还使用 np.argmax() 将目标转换为稀疏值,从而处理单击编码目标。
我们可以在上述完整脚本的末尾添加以下内容,以计算其准确性:
# Calculate accuracy from output of activation2 and targets
# calculate values along first axis
predictions = np.argmax(activation2.output, axis=1)if len(y.shape) == 2:y = np.argmax(y, axis=1)accuracy = np.mean(predictions==y)# Print accuracy
print('acc:', accuracy)
>>>
acc: 0.34
现在,您已经学会了如何对我们的网络进行前向传递,并计算出模型是否表现不佳的指标信号,我们将在下一章开始进行优化!
本章的章节代码、更多资源和勘误表:https://nnfs.io/ch5
相关文章:

用 Python 从零开始创建神经网络(五):损失函数(Loss Functions)计算网络误差
用损失函数(Loss Functions)计算网络误差 引言1. 分类交叉熵损失(Categorical Cross-Entropy Loss)2. 分类交叉熵损失类(The Categorical Cross-Entropy Loss Class)展示到目前为止的所有代码3. 准确率计算…...

[CKS] K8S RuntimeClass SetUp
最近准备花一周的时间准备CKS考试,在准备考试中发现有一个题目关于RuntimeClass创建和挂载的题目。 专栏其他文章: [CKS] Create/Read/Mount a Secret in K8S-CSDN博客[CKS] Audit Log Policy-CSDN博客 -[CKS] 利用falco进行容器日志捕捉和安全监控-CSDN博客[CKS…...

【Python爬虫实战】轻量级爬虫利器:DrissionPage之SessionPage与WebPage模块详解
🌈个人主页:易辰君-CSDN博客 🔥 系列专栏:https://blog.csdn.net/2401_86688088/category_12797772.html 目录 前言 一、SessionPage (一)SessionPage 模块的基本功能 (二)基本使…...

计算机网络-2.1物理层
文章目录 通信的基础概念信源、信宿、信号、信道码元、速率、波特带宽(Hz) 奈奎斯特采样定律和香农采样定律编码&解码,调制&解调常用的编码方法常用的调制方法 传输介质1. 导向型传输介质2. 非导向型传输介质物理层接口的特性 物理层…...
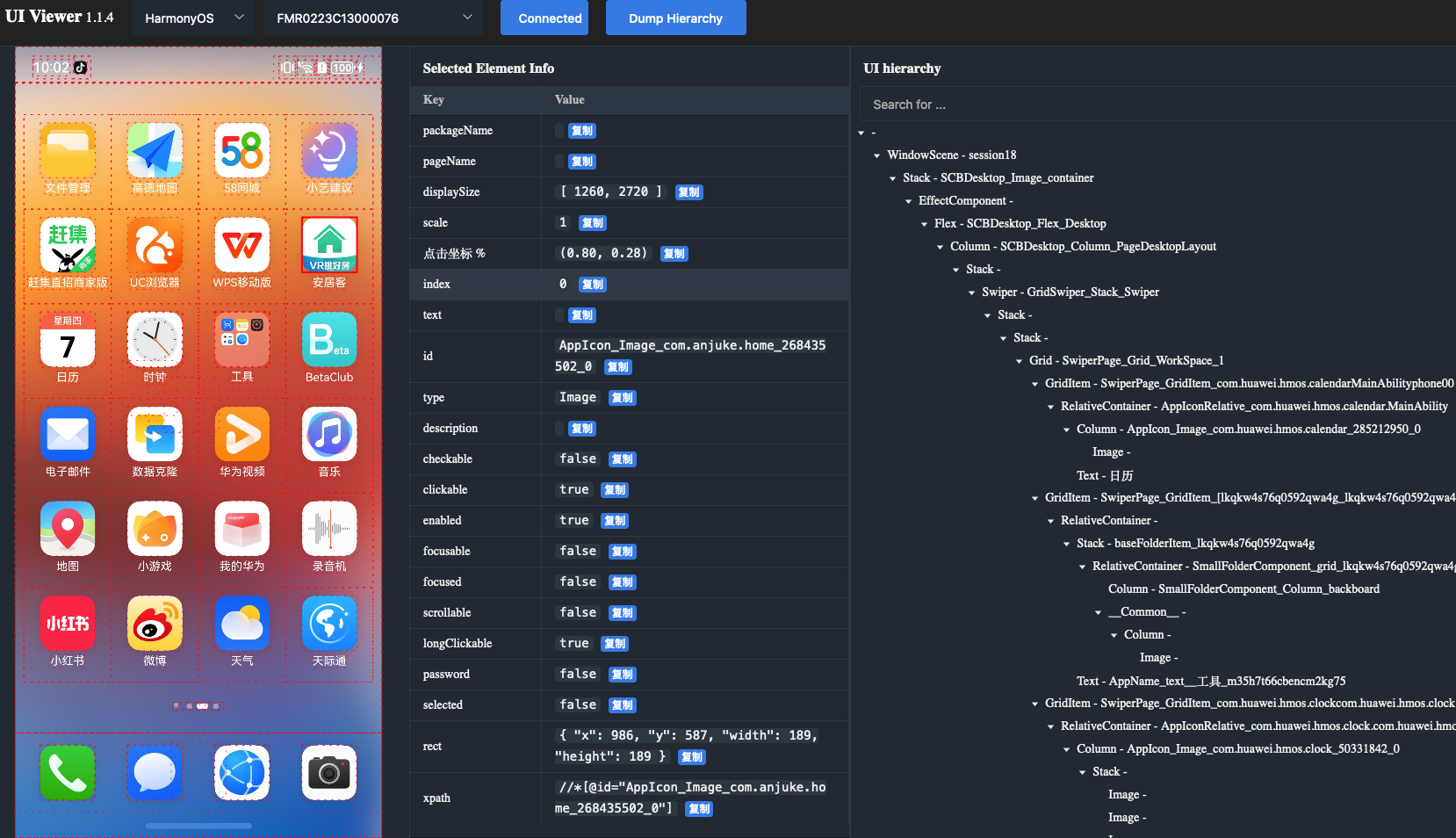
纯血鸿蒙系统 HarmonyOS NEXT自动化测试实践
1、测试框架选择 hdc:类似 android 系统的 adb 命令,提供设备信息查询,包管理,调试相关的命令ohos.UiTest:鸿蒙 sdk 的一部分,类似 android sdk 里的uiautomator,基于 Accessibility 服务&…...

C 语言标准库 - <errno.h>
目录 1.errno 变量 2.宏 1.errno 变量 errno.h 声明了一个 int 类型的 errno 变量,用来存储错误码(正整数)。 如果这个变量有非零值,表示已经执行的程序发生了错误。 #include <errno.h> #include <stdio.h> #in…...

Golang自带的测试库testing的使用
testing是golang自带的测试库。 testting规则: 在待测试功能所在文件的同级目录中创建一个以_test.go结尾的文件。 测试函数名必须是TestXxxx这个形式,而且Xxxx必须以大写字母开头,另外函数带有一个*testing.T类型的参数。 // 单元测试&am…...

29.电影院售票系统(基于springboot和vue的Java项目)
目录 1.系统的受众说明 2 论文背景 2.1 国内研究现状: 2.2 国外研究现状: 2.3 所用技术 3 系统需求分析 3.1 需求分析 3.2 可行性分析 3.2.1技术可行性分析 3.2.2市场可行性分析 3.2.3经济可…...

大学生就业平台微信小程序
随着计算机技术的成熟,互联网的建立,如今,PC平台上有许多关于大学生就业方面的程序,但由于使用时间和地点上的限制,用户在使用上存在着种种不方便,而开发一款大学生就业平台微信小程序,能够有效…...

Redis 缓存击穿
目录 缓存击穿 什么是缓存击穿? 有哪些解决办法? 缓存穿透和缓存击穿有什么区别? 缓存雪崩 什么是缓存雪崩? 有哪些解决办法? 缓存预热如何实现? 缓存雪崩和缓存击穿有什么区别? 如何保…...
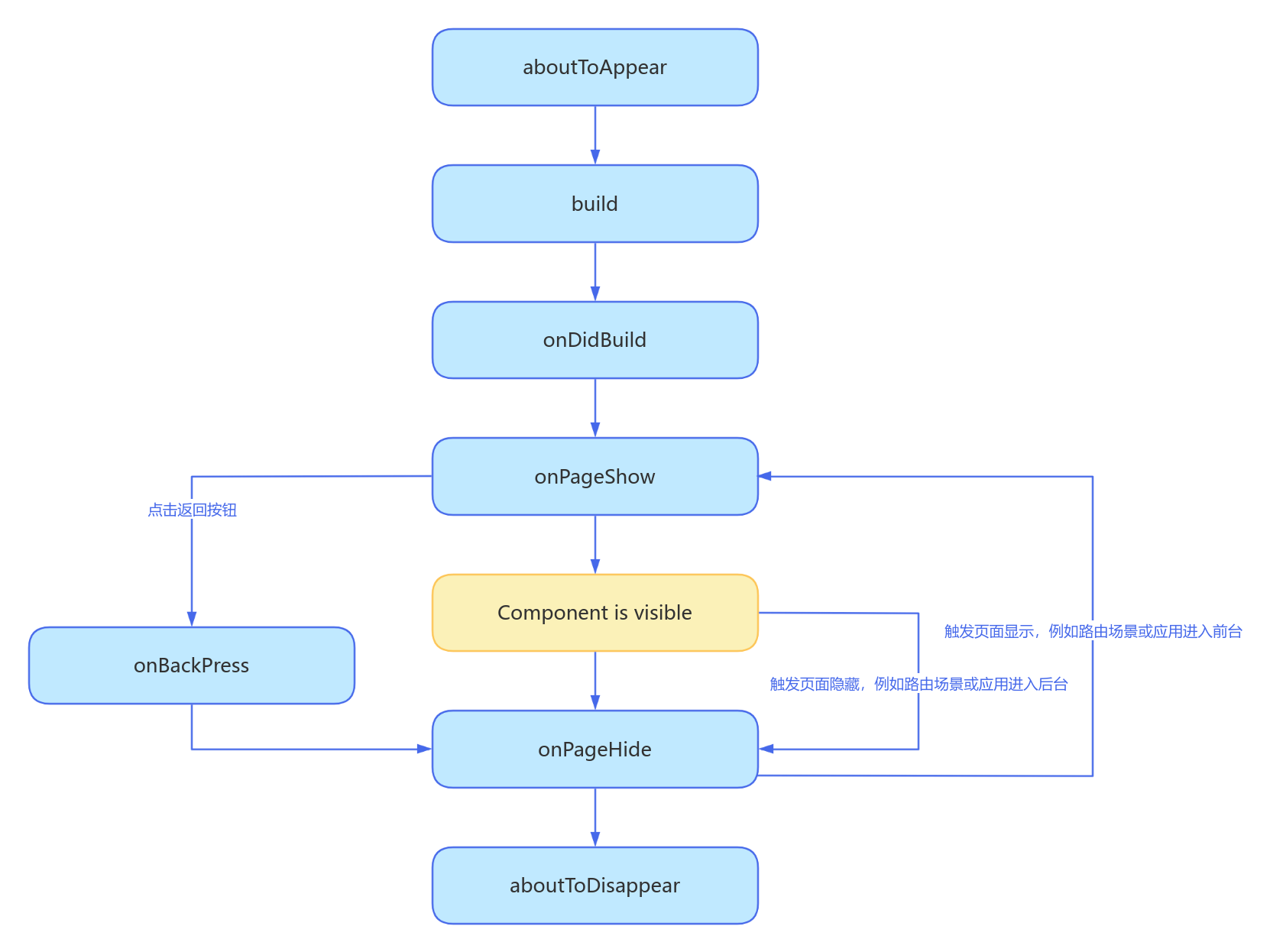
初探鸿蒙:从概念到实践
一、鸿蒙开发的环境准备 开发工具:使用 DevEco Studio,支持 ArkTS 语法。 系统要求:确保计算机符合 DevEco Studio 的最低系统需求。安装步骤:下载 DevEco Studio,安装合适的 SDK 和模拟器 二、鸿蒙应用可以…...

PHP API的路由设计思路
PHP API的路由设计是构建高效、可维护API的关键环节。以下是一套完整的PHP API路由设计思路: 一、明确设计原则 使用统一资源标识符(URI):通过URI来标识资源,确保每个资源都有一个唯一的地址。使用HTTP方法ÿ…...

工程师 - 如何访问Github
Github无法访问,涉及到IP地址、Host文件、DNS等配置。 1,查找github地址 打开https://www.ipaddress.com/网站,这个网站首页是查询自己IP的。 在上方搜索栏输入github.com,查找github的地址。 https://www.ipaddress.com/websit…...

222. 完全二叉树的节点个数 迭代
222. 完全二叉树的节点个数 已解答 简单 相关标签 相关企业 给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。 完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值࿰…...

中心极限定理的三种形式
独立同分布的中心极限定理: 设 X 1 , X 2 , … , X n X_1, X_2, \ldots, X_n X1,X2,…,Xn是独立同分布的随机变量序列,且 E ( X i ) μ E(X_i) \mu E(Xi)μ, D ( X i ) σ 2 > 0 D(X_i) \sigma^2 > 0 D(Xi)σ2>0存在…...

React Native 全栈开发实战班 - 导航栈定制
在 React Native 应用中,导航栈管理是实现页面跳转和状态维护的核心机制。React Navigation 提供了强大的导航栈管理功能,允许开发者灵活地控制页面堆栈、传递参数、处理返回逻辑等。本章节将深入探讨导航栈的管理与定制,包括如何控制导航栈、…...

扬州BGP高防服务器可以给企业带来哪些好处?
扬州BGP服务器是目前江苏较为出名的高防机房,随着网络安全逐渐被企业所重视,扬州机房的也被大家进行选择,但是扬州BGP高防服务器除了可以帮助企业抵御网络攻击,还有着其他的帮助,下面就让我们来了解一下吧!…...

题目讲解15 合并两个排序的链表
原题链接: 合并两个排序的链表_牛客题霸_牛客网 思路分析: 第一步:写一个链表尾插数据的方法。 typedef struct ListNode ListNode;//申请结点 ListNode* BuyNode(int x) {ListNode* node (ListNode*)malloc(sizeof(ListNode));node->…...

leetcode92:反转链表||
给你单链表的头指针 head 和两个整数 left 和 right ,其中 left < right 。请你反转从位置 left 到位置 right 的链表节点,返回 反转后的链表 。 示例 1: 输入:head [1,2,3,4,5], left 2, right 4 输出:[1,4,3,2…...

arkUI:遍历数据数组动态渲染(forEach)
arkUI:遍历数据数组动态渲染(forEach) 1 主要内容说明2 相关内容2.1 ForEach 的基本语法2.2 简单遍历数组2.2 多维数组遍历2.4 使用唯一键2.5 源码1的相关说明2.5.1 源码1 (遍历数据数组动态渲染)2.5.2 源码1运行效果 …...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...
