Python模拟A卷实操题
1.某机械公司生产两种产品。A的单件利润分别是100元,B的单件利润是150元。 每种产品由三种材料构成,现给出每种材料的库存(库存小于100000),求利润最大的生产方案。输入说明:第一行给出生产每件A产品所需要的三种材料数量;第二行给出生产每件B产品所需要的三种材料数量;第三行给出三种材料的库存数量。输出说明:输出利润最大生产方案所对应的每种产品的生产数量(按照产品A、产品B的顺序)和利润最大值,每个数值间用空格隔开。输入样例:3125223046输出样例:21350。
# 导入线性规划求解库
from scipy.optimize import linprog
# 输入数据
# 每件产品A所需的三种材料数量
a_materials = [3, 1, 2]
# 每件产品B所需的三种材料数量
b_materials = [5, 2, 3]
# 三种材料的库存数量
material_stock = [30, 4, 6]
# 产品A和B的利润
profit = [100, 150]
# 将目标函数的系数取负,因为 linprog 默认求解最小值问题
c = [-profit[0], -profit[1]]
# 不等式约束矩阵,表示材料的使用限制
A = [[a_materials[0], b_materials[0]], # 材料一的约束[a_materials[1], b_materials[1]], # 材料二的约束[a_materials[2], b_materials[2]] # 材料三的约束
]
# 不等式约束向量
b = material_stock
# 变量的取值范围,x >= 0
x_bounds = (0, None)
# 求解线性规划问题
res = linprog(c, A_ub=A, b_ub=b, bounds=[x_bounds, x_bounds], method='highs')
# 输出结果
if res.success:num_A, num_B = res.xmax_profit = -res.funprint(f"最优生产方案:生产产品A的数量为 {int(num_A)},生产产品B的数量为 {int(num_B)}")print(f"最大利润为:{max_profit}")
else:
print("未找到最优解")(1)输入数据:定义每个产品A和B所需的三种材料数量、材料的库存数量以及产品A和B的利润。
(2)目标函数:linprog默认求解最小化问题,将利润系数取反,求最大化利润。
(3)约束条件:每种材料的使用量不能超过库存量。
(4)求解问题:使用linprog求解最优生产方案。
(5)输出结果:打印最优生产方案和最大利润。
2.输入一个包含N个整数的数组,从中找到连续M个数之积最小的数字组合。输入说明:第一行是两个正整数N(N<200) 和M(M<10);第二行是N个整数(每个数字Ni都是整数,且INil<1000),中间用空格分开。输出说明:最小的M个连续数字积及第一个数在数组中的位置(初始位置按1进行计算)。输入样例:10412345678910输出样例:241。
# 输入处理
n, m = map(int, input().split())
array = list(map(int, input().split()))# 初始化最小乘积和对应的起始位置
min_product = float('inf')
min_index = -1# 遍历数组,找出连续 m 个数的最小乘积
for i in range(n - m + 1):product = 1for j in range(m):product *= array[i + j]if product < min_product:min_product = productmin_index = i + 1 # 转换为从 1 开始计数# 输出结果
print(min_product, min_index)(1)输入处理:首行输入包含两个正整数 N 和 M,表示数组长度和需要寻找的连续元素个数;第二行输入是包含 N 个整数的数组。
(2)最小乘积计算:通过遍历数组,找出所有长度为 M 的连续子数组,并计算它们的乘积,更新最小乘积及其起始位置。
(3)输出结果:输出最小乘积及其起始位置(位置从 1 开始计数)。
3.输入一个包含N个整数的数组,从中找到连续M个数之和最大的数字组合。输入说明:第一行是两个正整数N(N<200)和M(M<20)第二行是N个整数(每个数字Ni都是整数,且Nil<100000),中间用空格分开输出说明:最大的M个连续数字和及第一个数在数组中的位置(初始位置按1进行计算)。输入样例10412345678910输出样例:347。
# 输入处理
n, m = map(int, input().split())
array = list(map(int, input().split()))# 初始化最大和及其对应的起始位置
max_sum = float('-inf')
max_index = -1# 遍历数组,找出连续 m 个数的最大和
for i in range(n - m + 1):current_sum = sum(array[i:i + m])if current_sum > max_sum:max_sum = current_summax_index = i + 1 # 转换为从 1 开始计数# 输出结果
print(max_sum, max_index)(1)输入处理:第一行输入包含两个正整数 N 和 M,表示数组长度和需要寻找的连续元素个数;第二行输入是包含 N 个整数的数组。
(2)最大和计算:通过遍历数组找出所有长度为 M 的连续子数组,并计算它们的和,更新最大和及其起始位置。
(3)输出结果:输出最大和及其起始位置(位置从 1 开始计数)。
4.给定两个整数N和M(0<n<m<100000),求n到m中满足如下条件的数字,该数字与相邻的前、后数字之和可以被5整除,比如n=4,m=11时,5、10是满足条件的,而6、7、8、9不满足,4和11因为前、后数字不在1到n中,不参与统计。=""输入说明:两个正整数n和m(n<m<100000)=""输出说明:满足要求的数字,如果有多个满足条件的数字,按出现次序输出前3个,如果不足3个,用-1补充。=""输入样例1:14=100=""输出样例1:15=""20=""25=""输入样例2。
# 输入处理
n, m = map(int, input().split())# 满足条件的数字列表
result = []# 遍历 n 到 m 范围内的所有数字
for i in range(n, m + 1):last_digit = i % 10 # 获取数字的最后一位if last_digit != 0 and i % last_digit == 0 and i % 5 == 0:result.append(i)# 如果找到的数字少于 3 个,使用 -1 填充
while len(result) < 3:result.append(-1)# 输出前 3 个满足条件的数字
print(result[:3])(1)输入处理:输入两个整数 N 和 M,表示范围 [N, M]。
(2)条件检查:遍历范围内的每个数字,检查最后一位不为 0、该数字能被其最后一位整除、并且能被 5 整除的条件。
(3)输出处理:如果找到的数字少于 3 个,则使用 -1 填充,最后输出前 3 个满足条件的数字。
相关文章:

Python模拟A卷实操题
1.某机械公司生产两种产品。A的单件利润分别是100元,B的单件利润是150元。 每种产品由三种材料构成,现给出每种材料的库存(库存小于100000),求利润最大的生产方案。输入说明:第一行给出生产每件A产品所需要…...
Leetcode 检测相邻递增子数组
3349. 检测相邻递增子数组 I 给你一个由 n 个整数组成的数组 nums ,请你找出 k 的 最大值,使得存在 两个 相邻 且长度为 k 的 严格递增 子数组 。具体来说,需要检查是否存在从下标 a 和 b (a < b) 开始的 两个 子数组,并满…...

rockylinux 8安装 gcc11.2
方法 1:从源代码编译安装最新版本的 GCC 下载 GCC 源代码: 访问 GCC 官方网站下载最新版本的源代码,例如: wget https://ftp.gnu.org/gnu/gcc/gcc-11.2.0/gcc-11.2.0.tar.gz tar -xf gcc-11.2.0.tar.gz cd gcc-11.2.0安装依赖项&a…...
-奇数序列排序)
【蓝桥等考C++真题】蓝桥杯等级考试C++组第13级L13真题原题(含答案)-奇数序列排序
C L13 奇数序列排序 给定一个长度为N的正整数序列, 请将其中的所有奇数取出,并按增序(从小到大)输出。 输入: 共2行 第1行是一个正整数 N(不大于500); 第2行有 N 个正整数&#x…...

【AI】好用的AI记录
好用的AI 一、国内 KIMI通义 二、国外 GPT4Cursorv0...

linux安装boost.python
前言 boost.python库被用于C与Python代码间的交互,提供了两者间大部分数据类型的转换 相关环境 操作系统:Ubuntu 20.04 python版本:Python 3.8 boost版本:boost 1.78.0 安装 1.boost.python检查与卸载 在安装boost之前需要检…...

AI 扩展开发者思维方式:以 SQL 查询优化为例
在现代软件开发中,AI 技术的兴起让开发者的思维方式发生了显著变化。尤其是在 SQL 查询优化、代码重构以及算法设计等领域,AI 提供的建议不仅扩展了开发者的思考路径,还帮助他们发现以往没有意识到的潜在解决方案。 1. 传统思维模式下的 SQL…...
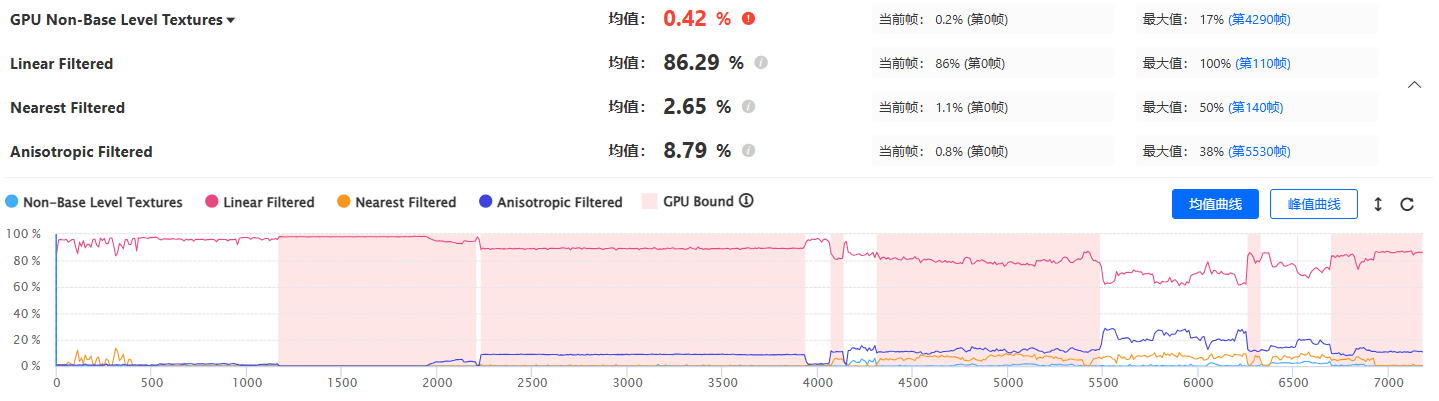
自定义面板,高效的游戏性能分析利器
为了更有效地聚焦并解决性能问题,UWA报告采用了分模块监控策略,确保每个模块独立成章,各司其职。然而,随着对性能分析需求的不断升级,我们已经意识到,在深入分析某些跨模块的性能瓶颈或优化点时,…...

【Linux进程特别篇】深度理解辨识僵尸进程和孤儿进程
--------------------------------------------------------------------------------------------------------------------------------- 每日鸡汤:每一份坚持都是成功的积累,只要相信自己,总会遇到惊喜。 -----------------------------…...

喜报|超维机器人荣获昇腾AI创新大赛铜奖
近日,在备受瞩目的昇腾AI创新大赛中,超维机器人凭借扎实的技术实力和创新产品,荣获大赛铜奖。这一荣誉不仅展现了超维机器人在智能巡检领域的技术创新与突破,也标志着超维机器人的智能巡检解决方案在人工智能领域获得了广泛认可&a…...

从五种架构风格推导出HTTP的REST架构
在分布式系统中,架构风格(Architectural Style)决定了系统组件如何交互、通信、存储和管理数据。每种架构风格都有其独特的特性和适用场景。本文将从五种典型的架构风格出发,逐步探讨它们如何影响了REST(Representational State Transfer,表述性状态转移)架构风格的设计…...

vue-h5:在h5中实现相机拍照加上身份证人相框和国徽框
方案1:排出来照片太糊了,效果不好 1.基础功能 参考: https://blog.csdn.net/weixin_45148022/article/details/135696629 https://juejin.cn/post/7327353533618978842?searchId20241101133433B2BB37A081FD6A02DA60 https://www.freesio…...

免费HTML模板和CSS样式网站汇总
HTML模板:(注意版权,部分不可商用) 1、Tooplate,免费HTML模板下载 Download 60 Free HTML Templates for your websitesDownload 60 free HTML website templates or responsive Bootstrap templates instantly from T…...
备份特殊文件)
Mac打开time machine(时间机器)备份特殊文件
Mac 打开time machine(时间机器)备份特殊文件 设置“时间机器”的作用具体操作办法 前言:今天在使用Nas同步文件时发现有部分重要文件没有同步,为了省事手动拖拽复制文件,导致其中一份非常重要的文件丢失,尝…...

Qt 学习第十六天:文件和事件
一、创建widget对象(文件) 二、设计ui界面 放一个label标签上去,设置成box就可以显示边框了 三、新建Mylabel类 四、提升ui界面的label标签为Mylabel 五、修改mylabel.h,mylabel.cpp #ifndef MYLABEL_H #define MYLABEL_H#incl…...

nvm 切换 Node.js 版本
nvm 切换 Node.js 版本 0. nvm 安装1. 查看装了哪些 Node.js 版本2. 安装 Node.js 版本安装最新稳定版本.安装个18 3. 切换 Node.js 版本4. 设置默认 Node.js 版本5. 卸载 Node.js 版本6.与项目的配合使用参考资料 0. nvm 安装 安装教程就不写了,直接看别人的。 脚…...

AI绘图最强软件stable diffusion,一文带你迅速了解!
有需要stable diffusion整合包可以扫描下方,免费获取 01 — 什么是 SD Stable Difusion(简称 SD) 其三种概念。 1.用来指代稳定扩散(Stable Diffusion) 技术,如 Midjourney是基于Stable Difusion技术实现的就是指它运用了 Stable Diffusion 的技术原理。 …...

VMware重磅官宣!Workstation和Fusion彻底全部免费:支持商用
VMware 官网宣布:VMware Workstation Pro: Now Available Free for Personal Use 别问,问就是正版用户!!! VMware宣布,其桌面虚拟化产品VMware Workstation和VMware Fusion将对所有用户彻底免费࿰…...

CCS 学习记录
1.导入项目 在CCS菜单中选择Project->Import Existing CCS Eclipse Project,点击Browse找到CCS workspace所在文件夹,点击OK,CCS会自动将所选文件夹及其子文件夹下所有的CCS Projects列出。从列表中找到所要导入的项目文件夹,…...

241112.学习日志——[CSDIY] Cpp零基础速成 [01]
CSDIY:这是一个非科班学生的努力之路,从今天开始这个系列会长期更新,(最好做到日更),我会慢慢把自己目前对CS的努力逐一上传,帮助那些和我一样有着梦想的玩家取得胜利!!&…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...
