计算两个结构的乘法
在行列可自由变换的平面上,2点结构有3个
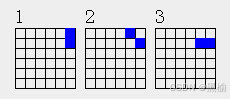
3点结构有6个
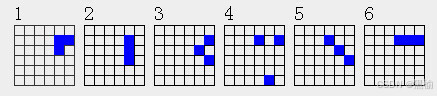
计算2*2
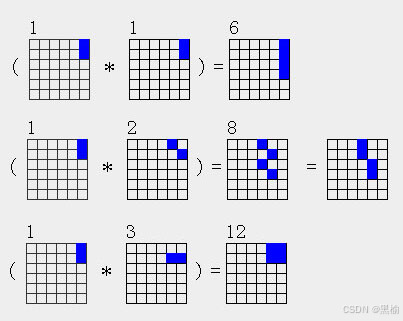
| 2a1*2a1=4a6 |
| 2a1*2a2=4a8 |
| 2a1*2a3=4a12 |
显然2a1*2a1=4a6因为这3个结构都分布在同一列上,就是整数乘法。2a1*2a2的结果有2种写法,一种外形像2a1细节为2a2,一种外形为2a2,细节为2a1.但这两个结构是相同的,所以可以被分解成两个结构积的结构有一种外形和细节的2重对称性。
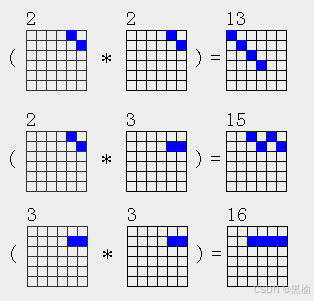
| 2a2*2a2=4a13 |
| 2a2*2a3=4a15 |
| 2a3*2a3=4a16 |
4点结构共有16个,其中只有6个可以被分解为两个结构的积,剩余的10个结构是类质数结构不能被分解。
计算3*2
3ax*2a1
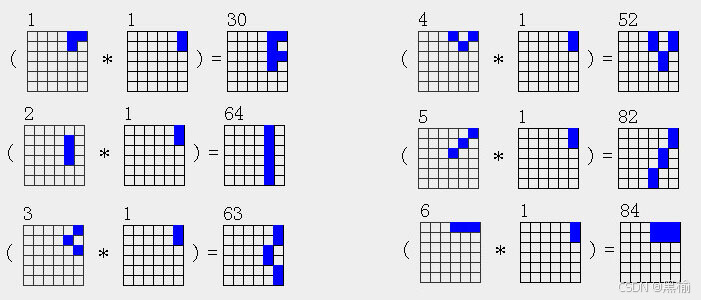
| 3a1*2a1=6a30 |
| 3a2*2a1=6a64 |
| 3a3*2a1=6a63 |
| 3a4*2a1=6a52 |
| 3a5*2a1=6a82 |
| 3a6*2a1=6a84 |
3ax*2a2
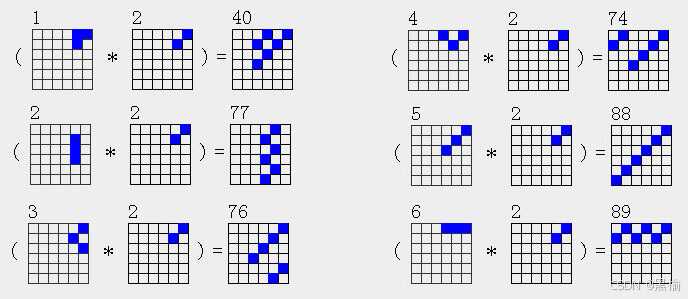
| 3a1*2a2=6a40 |
| 3a2*2a2=6a77 |
| 3a3*2a2=6a76 |
| 3a4*2a2=6a74 |
| 3a5*2a2=6a88 |
| 3a6*2a2=6a89 |
3ax*2a3
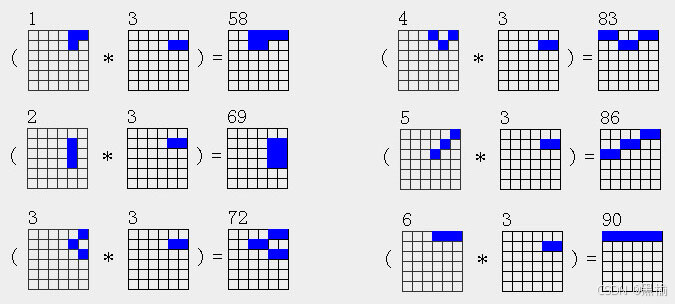
| 3a1*2a3=6a58 |
| 3a2*2a3=6a69 |
| 3a3*2a3=6a72 |
| 3a4*2a3=6a83 |
| 3a5*2a3=6a86 |
| 3a6*2a3=6a90 |
6点结构有90个,只有18个可被分解。
检验结构加法是否有结合律
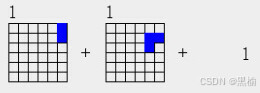
2a1+3a1+1
首先计算2a1+3a1

12(3a1+2a1)=5a1+2*5a3+5a4+5a9+3*5a10+2*5a12+2*5a24
让5a1,3,4,9,10,12,14分别+1

17(5a1+1)=4*5a2+3*5a3+5a4+5a6+5a9+4*5a12+5a15+2*5a30

12(5a3+1)=3*5a1+2*5a6+5a8+2*5a10+2*5a13+5a17+5a32
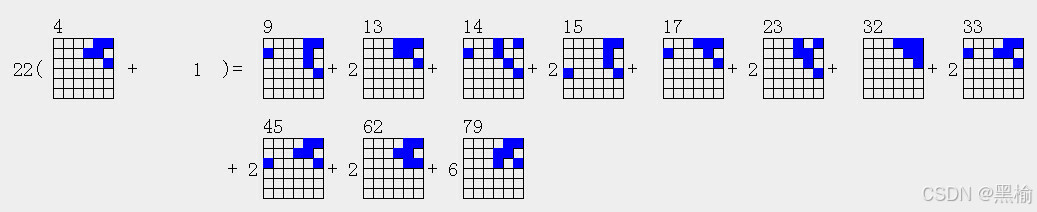
22(5a4+1)=5a9+2*5a13+5a14+2*5a15+5a17+2*5a23+5a32+2*5a33+2*5a45+2*5a62+6*5a79

23(5a9+1)=5a6+2*5a7+5a9+5a15+2*5a23+2*5a25+5a26+2*5a27+3*5a36+2*5a40+4*5a52+2*5a66

12(5a10+1)=5a3+5a22+2*5a28+2*5a30+4*5a31+2*5a42

13(5a12+1)=2*5a12+5a24+2*5a30+5a32+5a62+6*5a69

13(5a24+1)=5a13+5a32+5a41+2*5a58+6*5a84+2*5a85
考虑系数1,2,1,1,3,2,2把结果加起来
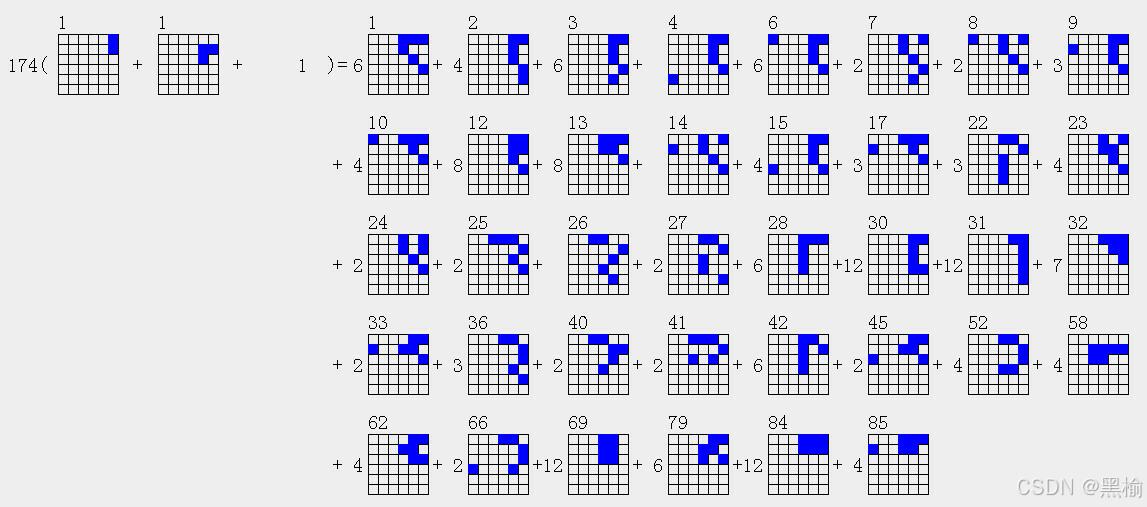
174(2a1+3a1+1)=6*5a1+4*5a2+6*5a3+5a4+6*5a6+2*5a7+2*5a8+3*5a9+4*5a10+8*5a12+8*5a13+5a14+4*5a15+3*5a17+3*5a22+4*5a23+2*5a24+2*5a25+5a26+2*5a27+6*5a28+12*5a30+12*5a31+7*5a32+2*5a33+3*5a36+2*5a40+2*5a41+6*5a42+2*5a45+4*5a52+4*5a58+4*5a62+2*5a66+12*5a69+6*5a79+12*5a84+4*5a85
第二种方法,先计算3a1+1

将4a1,2,3,4,12,14分别加2a1

18(4a1+2a1)=3*6a1+3*6a3+6a7+2*6a13+2*6a23+4*6a30+3*6a79
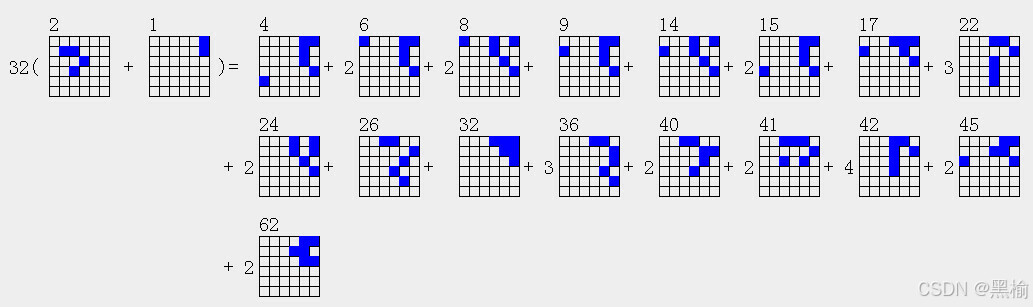
32(4a2+2a1)=6a4+2*6a6+2*6a8+6a9+6a14+2*6a15+6a17+3*6a22+2*6a24+6a26+6a32+3*6a36+2*6a40+2*6a41+4*6a42+2*6a45+2*6a62
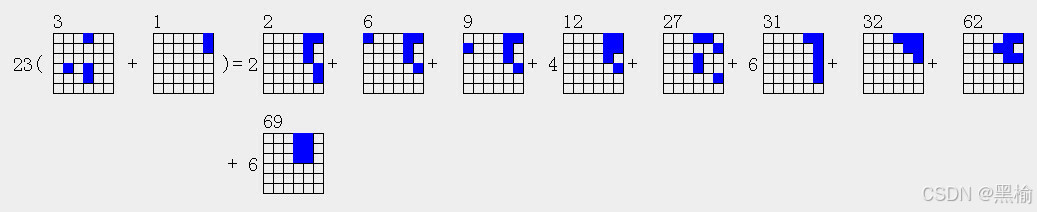
23(4a3+2a1)=2*6a2+6a6+6a9+4*6a12+6a27+6*6a31+6a32+6a62+6*6a69

11(4a4+2a1)=6a6+2*6a10+6a25+3*6a28+6a32+6a33+2*6a58

6(4a12+2a1)=6a13+6a30+6a52+3*6a84

7(4a14+2a1)=6a15+6a17+6a32+6a42+6a66+2*6a85
考虑系数把等式右侧相加和第一种方法得到的结构是一致的。由此至少有理由假设结构加法同样符合结合律。
验算乘法的结合律
计算
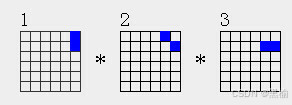
2a1*2a2*2a3

(2a1*2a2)*2a3=4a8*2a3=8a529

2a1*(2a2*2a3)=2a1*4a15=8a529
8a529这个结构有3重对称性。
所以有理由猜测结构乘法同样有结合律。
相关文章:

计算两个结构的乘法
在行列可自由变换的平面上,2点结构有3个 3点结构有6个 计算2*2 2a1*2a14a6 2a1*2a24a8 2a1*2a34a12 显然2a1*2a14a6因为这3个结构都分布在同一列上,就是整数乘法。2a1*2a2的结果有2种写法,一种外形像2a1细节为2a2,一种外形为2…...

学校服务器连接pycharm配置2
上一个可能还是有点问题,因为实际在跑的时候读取的其实是本地的anaconda,这个重新整了一下流程 首先在学校服务器先激活自己创建的虚拟环境,这里就不截图了 然后在pycharm里面打开设置 选择这个python解释器 这里有添加解释器 选择SSH …...

AI赋能电商:创新应用提升销售与用户体验
目录 一、引言 二、AI技术在电商领域的创新应用 三、AI技术提高电商销售效率和用户体验的实践路径 一、引言 随着人工智能(AI)技术的不断成熟,电商行业正迎来一场深刻的变革。AI技术在购物推荐、会员分类、商品定价等方面的创新应用&…...

详解kafka消息发送重试机制的案例
在 Kafka 生产者中实现消息发送的重试机制,可以通过配置 KafkaProducer 的相关属性来实现。以下是一些关键的配置项: retries:设置生产者发送失败后重试的次数。 retry.backoff.ms:设置生产者在重试前等待的时间。 buffer.memo…...

linux文本管理!!!
文章目录 第1章 文本过滤/查看命令1.echo:输出文本2.cat:合并文件或查看文件内容3.head:显示文件头部信息4.tail:显示文件尾部信息5.wc: 统计文本行号6.less:分页显示文件内容7.grep:文本过滤工具8.定向符号…...

软件设计师-计算机体系结构分类
计算机体系结构分类 Flynn分类法 根据不同的指令流数据流组织方式分类单指令流但数据流SISD,单处理器系统单指令多数据流SIMD,单指令流多数据流是一种采用一个控制器来控制多个处理器,同时对一组数据(又称“数据矢量”)中的每一…...

《基于深度学习的车辆行驶三维环境双目感知方法研究》
复原论文思路: 《基于深度学习的车辆行驶三维环境双目感知方法研究》 1、双目测距的原理 按照上述公式算的话,求d的话,只和xl-xr有关系,这样一来,是不是只要两张图像上一个测试点的像素位置确定,对应的深…...

jwt用户登录,网关给微服务传递用户信息,以及微服务间feign调用传递用户信息
1、引入jwt依赖 <dependency><groupId>io.jsonwebtoken</groupId><artifactId>jjwt</artifactId><version>0.9.1</version></dependency> 2、Jwt工具类,生成token以及解析token package com.niuniu.gateway.uti…...

ubontu安装anaconda
1.下载 Anaconda 安装脚本 2. 复制到服务器上/home/username文件夹中,进入文件夹,执行: bash Anaconda3-2024.10-1-Linux-x86_64.sh一直按回车,然后输入yes同意协议。 3. 初始化 Anaconda 环境,会自动配置环境变量&a…...

【Docker容器化技术】docker安装与配置、常用命令、容器数据卷、应用部署实战、Dockerfile、服务编排docker-compose、私有仓库
文章目录 一、Docker的安装与配置1、docker概述2、安装docker3、docker架构4、配置镜像加速器 二、Docker命令1、服务相关命令2、镜像相关命令3、容器相关命令 三、Docker容器数据卷1、数据卷概念及作用2、配置数据卷3、配置数据卷容器 四、Docker应用部署实战1、部署MySQL2、部…...

Python模拟A卷实操题
1.某机械公司生产两种产品。A的单件利润分别是100元,B的单件利润是150元。 每种产品由三种材料构成,现给出每种材料的库存(库存小于100000),求利润最大的生产方案。输入说明:第一行给出生产每件A产品所需要…...
Leetcode 检测相邻递增子数组
3349. 检测相邻递增子数组 I 给你一个由 n 个整数组成的数组 nums ,请你找出 k 的 最大值,使得存在 两个 相邻 且长度为 k 的 严格递增 子数组 。具体来说,需要检查是否存在从下标 a 和 b (a < b) 开始的 两个 子数组,并满…...

rockylinux 8安装 gcc11.2
方法 1:从源代码编译安装最新版本的 GCC 下载 GCC 源代码: 访问 GCC 官方网站下载最新版本的源代码,例如: wget https://ftp.gnu.org/gnu/gcc/gcc-11.2.0/gcc-11.2.0.tar.gz tar -xf gcc-11.2.0.tar.gz cd gcc-11.2.0安装依赖项&a…...
-奇数序列排序)
【蓝桥等考C++真题】蓝桥杯等级考试C++组第13级L13真题原题(含答案)-奇数序列排序
C L13 奇数序列排序 给定一个长度为N的正整数序列, 请将其中的所有奇数取出,并按增序(从小到大)输出。 输入: 共2行 第1行是一个正整数 N(不大于500); 第2行有 N 个正整数&#x…...

【AI】好用的AI记录
好用的AI 一、国内 KIMI通义 二、国外 GPT4Cursorv0...

linux安装boost.python
前言 boost.python库被用于C与Python代码间的交互,提供了两者间大部分数据类型的转换 相关环境 操作系统:Ubuntu 20.04 python版本:Python 3.8 boost版本:boost 1.78.0 安装 1.boost.python检查与卸载 在安装boost之前需要检…...

AI 扩展开发者思维方式:以 SQL 查询优化为例
在现代软件开发中,AI 技术的兴起让开发者的思维方式发生了显著变化。尤其是在 SQL 查询优化、代码重构以及算法设计等领域,AI 提供的建议不仅扩展了开发者的思考路径,还帮助他们发现以往没有意识到的潜在解决方案。 1. 传统思维模式下的 SQL…...
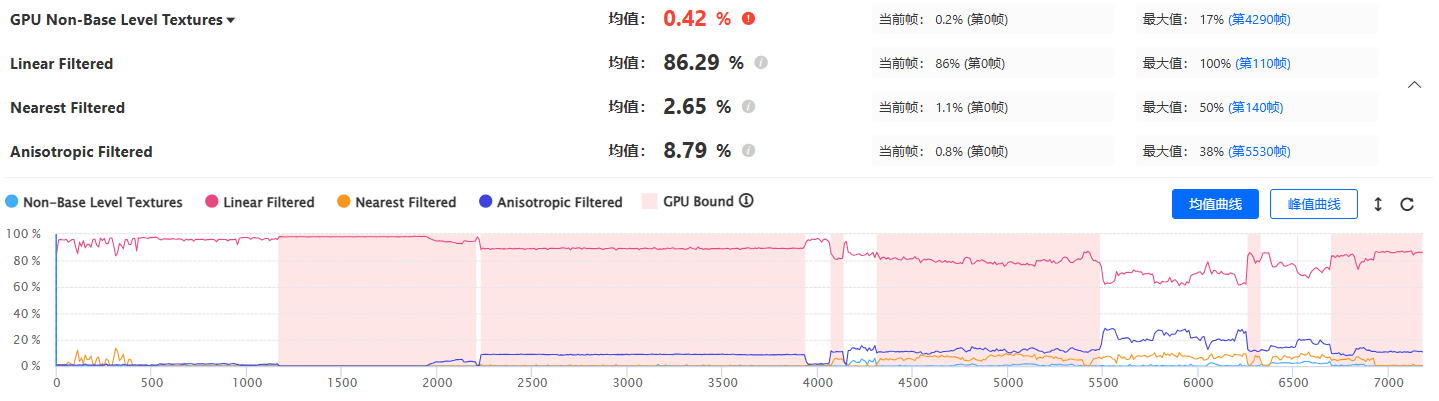
自定义面板,高效的游戏性能分析利器
为了更有效地聚焦并解决性能问题,UWA报告采用了分模块监控策略,确保每个模块独立成章,各司其职。然而,随着对性能分析需求的不断升级,我们已经意识到,在深入分析某些跨模块的性能瓶颈或优化点时,…...

【Linux进程特别篇】深度理解辨识僵尸进程和孤儿进程
--------------------------------------------------------------------------------------------------------------------------------- 每日鸡汤:每一份坚持都是成功的积累,只要相信自己,总会遇到惊喜。 -----------------------------…...

喜报|超维机器人荣获昇腾AI创新大赛铜奖
近日,在备受瞩目的昇腾AI创新大赛中,超维机器人凭借扎实的技术实力和创新产品,荣获大赛铜奖。这一荣誉不仅展现了超维机器人在智能巡检领域的技术创新与突破,也标志着超维机器人的智能巡检解决方案在人工智能领域获得了广泛认可&a…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...
