直方图均衡化及Matlab实现

直方图均衡化

直方图均衡化是一种图像增强技术，主要用于增强图像的对比度，特别是当图像的有用数据的对比度接近时效果显著。通过改变图像的直方图分布，直方图均衡化能够使图像的灰度值更加接近均匀分布，从而增加图像的整体对比度。‌

关键点及思路

直方图均衡化有两个关键点：

• 像素的强度顺序不变，也就是说经过一个灰度映射函数后，原本低强度值的像素依然比原本高强度值的像素强度低，即单调递增
• 变换后像素的直方图是接近均匀的，即每个等间隔灰度范围的像素个数基本相等。

这里不列举公式了（看也看不懂…），基于这两个关键点，直方图均衡化的思路其实很简单，就是基于原图像素灰度的累计概率分布（CDF）与变换后图像的累计概率分布（（CDF））保持一致，只是变换后的图像灰度范围是0-255，一般要比原图的灰度范围广。这样就达到了把原图的一小部分的灰度范围以一种近似均匀的方式扩散到整个0-255灰度范围。

Matlab实现

clc;clear;close all;%%调用自定义函数进行直方图均衡化
imageName = 'lena.png';
img = imread(imageName);
histeq_img = hisuni(img);
subplot(1,2,1);
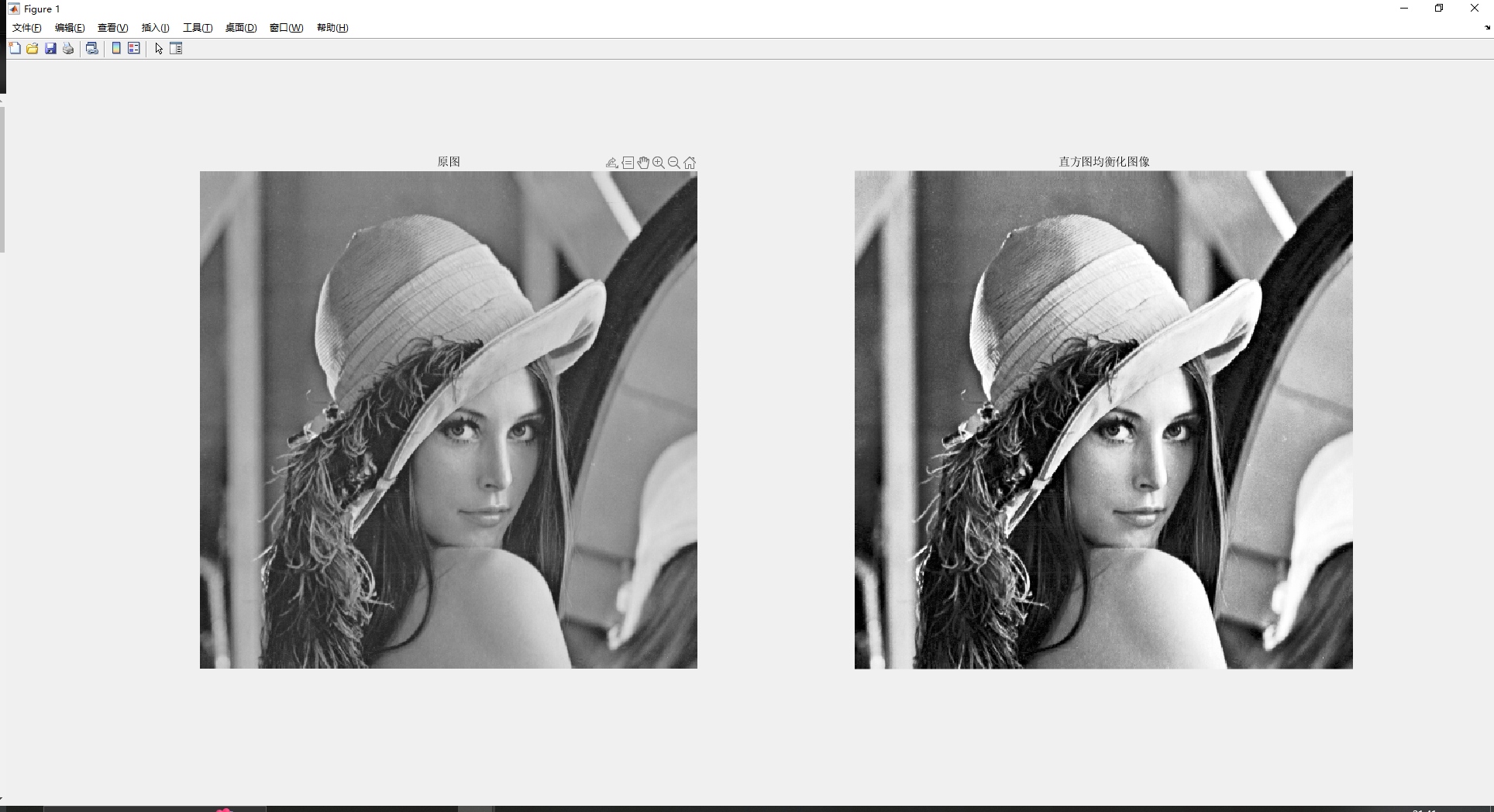
imshow(img);
title('原图');
subplot(1,2,2);
imshow(histeq_img);
title('直方图均衡化图像');%%绘制直方图
subplot(1,2,1);
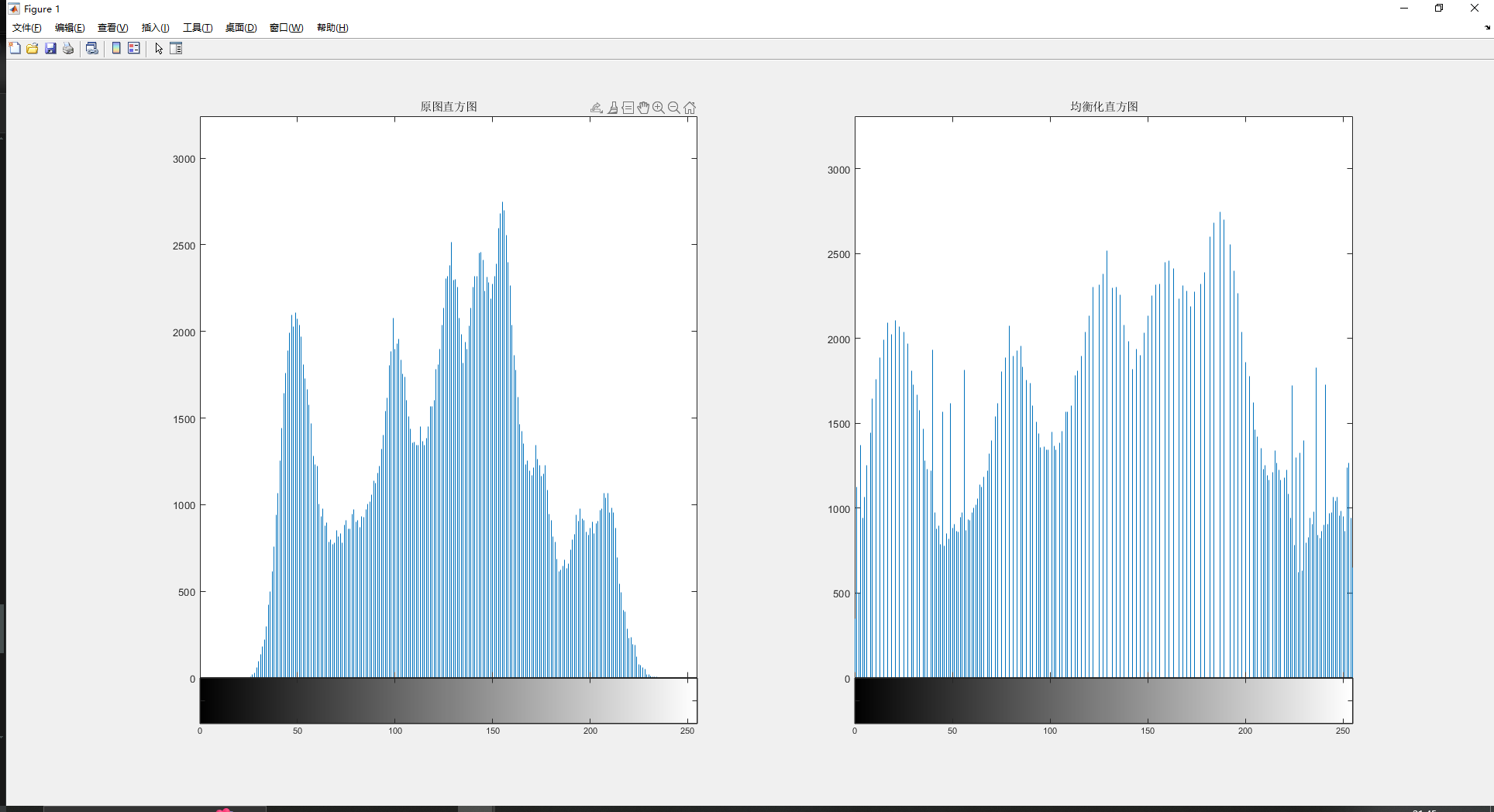
imhist(img);
title('原图直方图');
subplot(1,2,2);
imhist(histeq_img);
title('均衡化直方图');function new_image = hisuni(image)% 直方图均衡化函数% 输入: image - 输入的灰度图像% 输出: new_image - 均衡化后的图像[m, n] = size(image);% 计算直方图[Counts, ~] = histcounts(image(:), 0:256)% 计算概率密度函数 (PDF)pdf = Counts/(m*n)% 计算累积分布函数 (CDF)cdf = cumsum(pdf)% 生成映射表mapping = uint8(cdf * 255)% 初始化新图像new_image = zeros(size(image), 'uint8');% 对每个像素值进行映射for idx = 1:255new_image(image == idx - 1) = mapping(idx);end
end

当然matlab中也有内置函数histeq函数，直接对原图矩阵调用即可进行均衡化增强。