DP动态规划基础题(Kadane算法)
动态规划(Dynamic Programming,简称DP)是一种在数学、管理科学、计算机科学、经济学和生物信息学等领域中使用的,通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。动态规划算法通常用于优化问题,特别是那些具有重叠子问题和最优子结构性质的问题。
动态规划的基本思想
重叠子问题:动态规划算法中,问题被分解成多个子问题,而这些子问题会重复出现多次。如果这些子问题的结果可以被保存下来,那么当它们再次出现时,可以直接使用之前的结果,而不需要重新计算。
最优子结构:一个问题的最优解包含其子问题的最优解。这意味着,如果我们能够找到所有子问题的最优解,那么就能构造出原问题的最优解。
动态规划的步骤
定义状态:确定dp数组(或dp表)中的状态表示什么。通常,状态是问题规模的一个或多个参数。
确定状态转移方程:找出状态之间的关系,即如何从一个或多个较小子问题的解构造出当前问题的解。
确定初始状态和边界条件:确定dp数组的初始值,以及问题的边界条件。
计算顺序:确定如何迭代地填充dp数组,通常从小到大或从上到下。
构造最优解:一旦dp数组被填充,就可以通过它来构造问题的最优解。
动态规划的简单例子
斐波那契数列:计算第n个斐波那契数,其中斐波那契数列定义为:F(0) = 0, F(1) = 1, F(n) = F(n-1) + F(n-2)。
状态:dp[i] 表示第i个斐波那契数。
状态转移方程:dp[i] = dp[i-1] + dp[i-2]。
初始状态和边界条件:dp[0] = 0, dp[1] = 1。
计算顺序:从i = 2到n,依次计算dp[i]。
通过动态规划,我们可以避免重复计算子问题,从而提高算法的效率。动态规划适用于许多问题,如背包问题、最长公共子序列问题、最短路径问题等。
翻转增益的最大子数组和 -
链接: 翻转增益的最大子数组和
题目:
问题描述
给定整数数组,我们称其中连续的 0 个或多个整数为一个子数组,求翻转任一子数组后,新数组中子数组的和的最大值
输入格式
第一行输入为 N,代表数组长度
第二行输入为 N 个整数,依次为数组的每个元素
输出格式
一个整数 K,代表所有可能新数组中子数组的和的最大值
输入样例
5
1 2 3 -1 4
输出样例
10
说明
选择翻转子数组 [-1, 4] 或 [1, 2, 3, -1],新数组分别是 [1, 2, 3, 4, -1] 和 [-1, 3, 2, 1, 4],二者的子数组最大和都是 10
数据范围
50% case:1 <= N <= 100, -100<= arr[i] <= 100
100% case:1 <= N <= 1e6, -100<= arr[i] <= 100
思路:
问题理解
给定一个整数数组,我们可以翻转任意一个子数组(即子数组中的元素顺序颠倒),然后计算新数组中所有子数组的和的最大值。
解题思路
初始子数组和:
首先,计算原始数组中所有子数组的和的最大值。这可以通过Kadane算法来实现。
翻转子数组的影响:
翻转一个子数组会影响该子数组及其周围的子数组的和。我们需要找到一个翻转子数组的方式,使得新数组中子数组的和最大。
计算翻转后的最大子数组和:
对于每个可能的翻转子数组,计算翻转后的新数组中所有子数组的和的最大值。
选择所有可能翻转子数组中,使得新数组中子数组和最大的那个。
关键步骤
Kadane算法:
使用Kadane算法计算原始数组的最大子数组和。
翻转子数组的影响:
对于每个可能的翻转子数组,计算翻转后的新数组中所有子数组的和的最大值。
这可以通过计算翻转子数组的前后部分的最大子数组和来实现。
综合考虑:
综合考虑原始数组的最大子数组和以及所有可能翻转子数组后的最大子数组和,选择最大的那个作为最终答案
Kadane算法是一种用于求解最大子数组和的经典算法。它的核心思想是通过动态规划来逐步计算当前子数组的和,并记录最大子数组的和。
Kadane算法的工作原理
初始化:
初始化两个变量:maxEndingHere 和 maxSoFar。
maxEndingHere 表示以当前元素结尾的最大子数组和。
maxSoFar 表示全局的最大子数组和。
遍历数组:
从数组的第一个元素开始遍历,逐步更新 maxEndingHere 和 maxSoFar。
对于每个元素 array[i],更新 maxEndingHere 为 max(array[i], maxEndingHere + array[i])。
这意味着如果当前元素 array[i] 比 maxEndingHere + array[i] 大,则从当前元素开始重新计算子数组和。
更新 maxSoFar 为 max(maxSoFar, maxEndingHere)。
这意味着记录全局的最大子数组和。
返回结果:
遍历结束后,maxSoFar 即为最大子数组和。
private static int kadane(int[] array) {int maxEndingHere = array[0];int maxSoFar = array[0];for (int i = 1; i < array.length; i++) {maxEndingHere = Math.max(array[i], maxEndingHere + array[i]);maxSoFar = Math.max(maxSoFar, maxEndingHere);}return maxSoFar;
}通过代码:
java 代码解读复制代码public class Main {public static int solution(int N, int[] data_array) {// 计算原始数组的最大子数组和int originalMaxSum = kadane(data_array);// 计算翻转子数组后的最大子数组和int maxSumAfterFlip = originalMaxSum;for (int i = 0; i < N; i++) {for (int j = i; j < N; j++) {// 翻转子数组 [i, j]int[] flippedArray = flipSubarray(data_array, i, j);// 计算翻转后的最大子数组和int flippedMaxSum = kadane(flippedArray);// 更新最大值maxSumAfterFlip = Math.max(maxSumAfterFlip, flippedMaxSum);}}return maxSumAfterFlip;}// Kadane算法计算最大子数组和private static int kadane(int[] array) {int maxEndingHere = array[0];int maxSoFar = array[0];for (int i = 1; i < array.length; i++) {maxEndingHere = Math.max(array[i], maxEndingHere + array[i]);maxSoFar = Math.max(maxSoFar, maxEndingHere);}return maxSoFar;}// 翻转子数组 [start, end]private static int[] flipSubarray(int[] array, int start, int end) {int[] flippedArray = array.clone();while (start < end) {int temp = flippedArray[start];flippedArray[start] = flippedArray[end];flippedArray[end] = temp;start++;end--;}return flippedArray;}public static void main(String[] args) {// 测试用例int N = 4;int[] data_array = {-3, -1, -2, 3};System.out.println(solution(N, data_array)); // 预期输出: 3}
}
。
相关文章:
)
DP动态规划基础题(Kadane算法)
动态规划(Dynamic Programming,简称DP)是一种在数学、管理科学、计算机科学、经济学和生物信息学等领域中使用的,通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。动态规划算法通常用于优化问题,特别是那…...

[UnLua]动态创建SceneCapture2d相机,并且添加渲染目标纹理
在 Unlua 开发中,相机相关的操作是构建场景视觉效果的重要部分。以下我们来详细分析一段涉及相机实例化和为相机赋予纹理目标的 Unlua 代码。 -- 实例化相机local World self:GetWorld()maskCamera World:SpawnActor(UE.ASceneCapture2D)-- 给相机赋值纹理目标lo…...
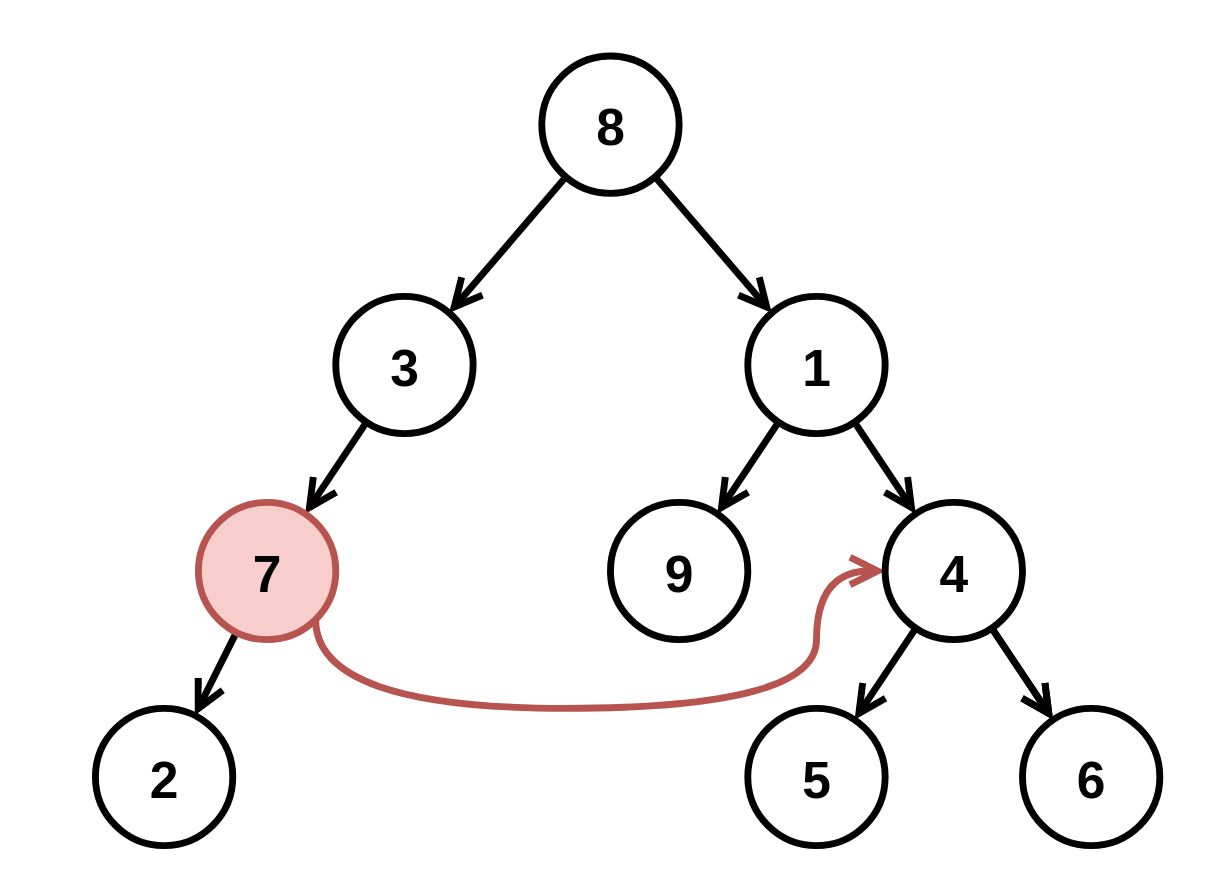
【leetcode练习·二叉树】用「分解问题」思维解题 I
本文参考labuladong算法笔记[【强化练习】用「分解问题」思维解题 I | labuladong 的算法笔记] 105. 从前序与中序遍历序列构造二叉树 | 力扣 | LeetCode | 给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵…...

【gitlab-ce】各组件介绍
主要组件功能接介绍(chatgpt回答的) nginx:作为Web服务器和反向代理,用于访问GitLab的Web界面。可以关闭,但会导致无法通过Web界面访问GitLab。prometheus_monitoring:提供监控和报警功能,收集和…...

PostgreSQL分区表:基础语法与运维实践
引言 简介:什么是数据库分区 数据库分区是一种将大型表物理上分割成多个较小的部分的技术。每个部分称为一个分区,这些分区可以分布在不同的存储设备上,以提高查询性能和管理效率。 为什么使用分区表 提高查询性能:通过减少需…...

Docker入门系列——DockerFile的使用
前面了解了Docker的基本概念,今天来认识一下DockerFile。 Dockerfile 是一个文本文件,包含一系列指令来组装 Docker 镜像。每个指令执行一个特定动作,例如安装包、复制文件或定义启动命令。正确使用 Dockerfile 指令对于构建高效容器至关重要…...
数据集平台分享
Kaggle: Your Machine Learning and Data Science CommunityKaggle is the world’s largest data science community with powerful tools and resources to help you achieve your data science goals.https://www.kaggle.com/Kaggle 包含非常丰富的数据集和代码,…...

去地面算法——depth_clustering算法调试(1)
1 源码下载 论文: 《2016-Fast Range Image-Based Segmentation of Sparse 3D Laser Scans for Online Operation》 《2017-Efficient Online Segmentation for Sparse 3D Laser Scans》 代码:git链接 2 问题记录 2.1 无法找到qt问题 问题截图&…...

设计模式-七个基本原则之一-单一职责原则 + SpringBoot案例
单一职责原理:(SRP) 面向对象七个基本原则之一 清晰的职责:每个类应该有一个明确的职责,避免将多个责任混合在一起。降低耦合:通过将不同的职责分开,可以降低类之间的耦合度,提高系统的灵活性。易于维护:当…...

HWA高速辅助驾驶系统组成及功能场景
HWA最基本功能包括智能跟车、拨杆变道、压速变道、车道居中保持等功能,有效减轻驾驶疲劳。随着智能驾驶不断走向成熟,HWA升级到高速自动驾驶HWP,可实现智能避让汇入口、智能避让大车、分心/疲劳监测、智能进出匝道、智能判别易混分叉路口、智…...

SpringMVC学习笔记(一)
一、SpringMVC的基本概念 (一)三层架构和MVC 1、三层架构概述 我们的开发架构一般都是基于两种形式,一种是 C/S 架构,也就是客户端/服务器,另一种是 B/S 架构,也就是浏览器服务器。在 JavaEE 开发中&…...

kaggle 如何利用API下载数据集
首先 上传kaggle官网生成得 API 密钥: kaggle.json 文件。放到该代码同目录下,再运行一下代码。 注: 只需要修改下载竞赛数据集,就可以选择你的指定数据集。 jupyter文件运行 #首先 上传 kaggle.json 文件并设置 API 密钥 #再…...

第一个 Flutter 项目(1)共46节
前端开发工具vs code,安装Flutter sdk,如果你的下载速度比较慢,可以选择这个😄 flutter sdk 解压码:stwq 配置可以看这Flutter 新建工程一直等待 解决办法-CSDN博客 如果你是新的 Flutter 开发者,我们建…...

学术论文写作丨机器学习与深度学习
目录 第一章、ChatGPT-4o使用方法与技巧 第二章、ChatGPT-4o辅助文献检索、总结与分析 第三章、ChatGPT-4o辅助学术论文选题、创新点挖掘与实验方案设计 第四章、ChatGPT-4o辅助学术论文开题与大纲生成 第五章、ChatGPT-4o辅助学术论文写作马拉松活动介绍 第六章、ChatGP…...

导-4涉及的知识点
除了本课题,3D结构几何修复领域还有以下一些值得关注的研究: 1. **Poisson图像编辑**: 成功地将给定的纹理块融合到可能完全不同的背景图像上。 2. **张量投票(TV)框架**: - 讨论了使用张量投票框架进…...

从0开始深度学习(28)——序列模型
序列模型是指一类特别设计来处理序列数据的神经网络模型。序列数据指的是数据中的每个元素都有先后顺序,比如时间序列数据(股票价格、天气变化等)、自然语言文本(句子中的单词顺序)、语音信号等。 1 统计工具 前面介绍…...

vue2使用 <component> 标签动态渲染不同的表单组件
在后台管理系统中,涉及到大量表单信息的修改和新增。现在想对模板中代码做一些简单的优化。 1. 使用 v-for 循环简化表单项 可以将表单项的定义提取到一个数组中,然后使用 v-for 循环来生成这些表单项。这将减少重复代码,提高可维护性。 2…...

C#实现在windows上实现指定句柄窗口的指定窗口坐标点击鼠标左键和右键的详细情况
在Windows编程中,有时我们需要对特定窗口进行操作,比如模拟鼠标点击。这在自动化测试、脚本编写或某些特定应用程序的开发中尤为常见。本文将深入探讨如何在C#中实现对指定句柄窗口进行鼠标点击操作,包括左键和右键点击。我们会从理论背景开始…...

探索Python自动化新境界:Invoke库的神秘面纱
文章目录 **探索Python自动化新境界:Invoke库的神秘面纱**第一部分:背景介绍第二部分:Invoke库是什么?第三部分:如何安装Invoke库?第四部分:Invoke库函数使用方法1. 定义任务2. 执行任务3. 任务…...

CSS样式实现3D效果
CSS 3D效果是通过CSS3中的transform和perspective等属性来实现的。这些属性允许你创建具有深度感和三维外观的网页元素。以下是一些常见的CSS 3D效果及其实现方法: 1. 3D旋转(Rotate) 使用transform: rotateX(), rotateY(), rotateZ()来分别…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...
