Python数据分析NumPy和pandas（二十九、其他Python可视化工具）
与其他开源工具一样，在 Python 中创建图形有很多选项（太多了，无法一一列举）。自 2010 年以来，主要开发工作集中在创建用于在 Web 上发布交互式图形上。例如： Altair、Bokeh 和 Plotly 等工具，可以在 Python 中指定用于 Web 浏览器的动态交互式图形。如果要创建用于打印或 Web 的静态图形，建议使用 matplotlib 和基于 matplotlib 构建的库，例如 pandas 和 seaborn，以满足我们的开发和数据分析需求。
总结一下：这几次记录的的目标是学习使用 pandas、matplotlib 和 seaborn 进行一些基本的数据可视化。数据可视化是一个活跃的研究领域，值得我们更加深入的学习。后面将学习使用 pandas 进行数据聚合和分组操作。
相关文章：
Python数据分析NumPy和pandas（二十九、其他Python可视化工具）
与其他开源工具一样，在 Python 中创建图形有很多选项（太多了，无法一一列举）。自 2010 年以来，主要开发工作集中在创建用于在 Web 上发布交互式图形上。例如： Altair、Bokeh 和 Plotly 等工具，可…...
Unity中HDRP设置抗锯齿
一、以前抗锯齿的设置方式 【Edit】——>【Project Settings】——>【Quality】——>【Anti-aliasing】 二、HDRP项目中抗锯齿的设置方式 在Hierarchy中——>找到Camera对象——>在Inspector面板上——>【Camera组件】——>【Rendering】——>【Pos…...
Spring Boot实现文件上传与OSS集成：从基础到应用
目录 前言1. 文件上传的基础实现1.1 前端文件上传请求1.2 后端文件接收与保存 2. 集成第三方OSS服务2.1 准备工作2.2 编写OSS集成代码2.3 修改Controller实现文件上传至OSS 3. 文件上传的扩展：多文件上传与权限控制结语 前言 随着互联网应用的快速发展，…...
Python学习26天
集合 # 定义集合 num {1, 2, 3, 4, 5} print(f"num：{num}\nnum数据类型为：{type(num)}") # 求集合中元素个数 print(f"num中元素个数为：{len(num)}") # 增加集合中的元素 num.add(6) print(num) # {1,2,3,4,5,6} # 删除…...
linux startup.sh shutdown.sh （kkFileView）
linux启动脚本和关闭脚本startup.sh shutdown.sh （kkFileView） startup.sh DIR_HOME("/opt/openoffice.org3" "/opt/libreoffice" "/opt/libreoffice6.1" "/opt/libreoffice7.0" "/opt/libreoffice7.1&q…...
[MySQL]隐式类型转换
安全等号 <> 如果有参数为NULL，则除了相等比较运算符()，比较的结果为null。对于 nullnull，结果为true。 在select语句中，使用 时，结果不会包含值为 null 的记录，但如果使用安全等号 <> 来…...
面经总结1
文章目录 如何保证批量请求失败，只弹出一个toast1使用计数器：2使用标志变量： 如何减少项目里的if-else1使用多态2使用策略模式3使用字典映射4使用状态模式 babel-runtime 作用是啥如何实现 PDF 预览和下载1浏览器内置PDF阅读器2使用PDF.js库3…...
Oracle19C AWR报告分析之Instance Efficiency Percentages (Target 100%)
Oracle19C AWR报告分析之Instance Efficiency Percentages 一、分析数据二、详细分析2.1 Instance Efficiency Percentages (Target 100%)各项指标及其解释2.2 分析和总结 一、分析数据 二、详细分析 在 Oracle AWR (Automatic Workload Repository) 报告中，每个性能…...
数据结构--数组
一.线性和非线性 线性：除首尾外只有一个唯一的前驱和后继。eg：数组，链表等。 非线性：不是线性的就是非线性。 二.数组是什么？ 数组是一个固定长度的存储相同数据类型的数据结构，数组中的元素被存储在一…...
nrm的安装及使用
nrm的安装及使用 NRM（NPM Registry Manager）是一个用于快速切换npm（Node Package Manager）源的工具。npm是Node.js的包管理工具，用于安装、发布、管理Node.js包。由于网络原因，直接使用npm官方源ÿ…...
【MatLab手记】 --从0到了解超超超详过程！！！
文章目录 MatLab笔记一、命令行窗口二、变量命名规则三、数据类型1. 数字2. 字符与字符串3. 矩阵3.1 矩阵创建3.2 矩阵的修改和删除3.3 矩阵的拼接与重构重排3.4 矩阵的运算方法3.5 矩阵的下标 4. 元胞数组（类似数据容器）5. 结构体 四、逻辑与流程控制五…...
从零创建vue+elementui+sass+three.js项目
初始化： vue init webpack projectnamecd projectnamenpm install支持sass: npm install sass --save-dev npm install sass-loader7.1.0 --save-dev npm install node-sass4.12.0 --save-devbuild/webpack.base.conf.js添加 rules: [...,{test: /\.scss$/,loade…...
Linux通过使用scp和sftp发送或拉取文件
在通过 telnet 登录到远程服务器之后，你无法直接使用 telnet 发送文件。telnet 是一个纯文本协议，不支持文件传输。要发送文件，你需要使用其他工具，如 scp 或 sftp。以下是使用这两种工具发送文件的方法： 使用 scp 发…...
Jtti：服务器总是自动重启怎么办?
服务器总是自动重启可能是由于多种原因引起的，包括硬件故障、软件问题、配置错误或环境因素。以下是一些常见原因和相应的解决方案： 1. 硬件问题 电源故障：电源供应不稳定或电源模块故障可能导致服务器重启。 解决方案：检查电源供…...
北京大学c++程序设计听课笔记101
基本概念 程序运行期间，每个函数都会占用一段连续的内存空间。而函数名就是该函数所占内存区域的起始地址（也称“入口地址”）。我们可以将函数的入口地址赋给一个指针变量，使该指针变量指向该函数。然后通过指针变量就可以调用这个…...
一键生成本地SSL证书：打造HTTPS安全环境
一键生成本地SSL证书：打造HTTPS安全环境 日光下的寒林没有一丝杂质，空气里的冰冷仿佛来自故乡遥远的北国，带着一些相思，还有细微几至不可辨认的骆驼的铃声。–《心美，一切皆美》 在本地开发环境中启用 HTTPS 一直是许多…...
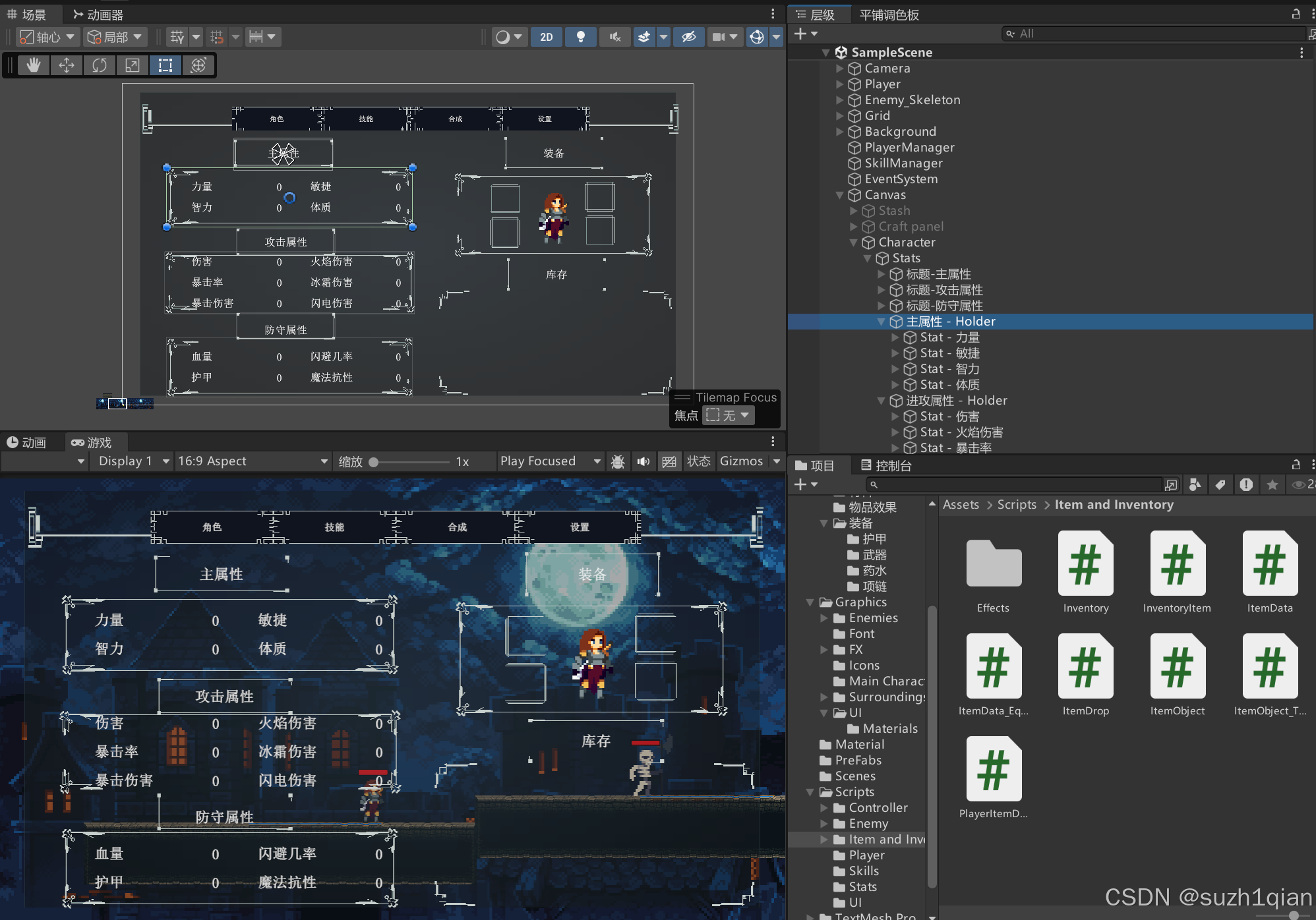
Unity类银河战士恶魔城学习总结（P124 CharacterStats UI玩家的UI）
【Unity教程】从0编程制作类银河恶魔城游戏_哔哩哔哩_bilibili 教程源地址：https://www.udemy.com/course/2d-rpg-alexdev/ 本章节实现了玩家属性栏，仓库，物品栏UI的制作 UI_StatSlot.cs 这个脚本是用来在Unity的UI上显示玩家属性…...
速盾：cdn 支持 php 吗？
在网络开发中，PHP 是一种广泛使用的服务器端脚本语言，用于创建动态网页和 web 应用程序。CDN（Content Delivery Network，内容分发网络）在内容分发方面具有强大的功能，那么它是否支持 PHP 呢？ C…...
在linux中使用nload实时查看网卡流量
在Linux系统中，可以使用多种工具来查看网卡流量。以下是一些常用的命令行工具： ifconfig：这是最基本的网络接口查看命令，但在最新的Linux发行版中，ifconfig命令已经被ip命令替代。 ip：用来查看和操作路由…...
【JavaEE进阶】Spring 事务和事务传播机制
目录 1.事务回顾 1.1 什么是事务 1.2 为什么需要事务 1.3 事务的操作 2. Spring 中事务的实现 2.1 Spring 编程式事务(了解) 2.2 Spring声明式事务 Transactional 对比事务提交和回滚的日志 3. Transactional详解 3.1 rollbackFor 3.2 Transactional 注解什么时候会…...
IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周，有很多同学在写期末Java web作业时，运行tomcat出现乱码问题，经过多次解决与研究，我做了如下整理： 原因： IDEA本身编码与tomcat的编码与Windows编码不同导致，Windows 系统控制台…...
【大模型RAG】拍照搜题技术架构速览：三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道（多模态 OCR → 语义检索 → 答案渲染）、两级检索（倒排 BM25 向量 HNSW）并以大语言模型兜底”的整体框架： 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后，分别用…...
python打卡day49
知识点回顾： 通道注意力模块复习空间注意力模块CBAM的定义 作业：尝试对今天的模型检查参数数目，并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...
脑机新手指南（八）：OpenBCI_GUI：从环境搭建到数据可视化（下）
一、数据处理与分析实战 （一）实时滤波与参数调整 基础滤波操作 60Hz 工频滤波：勾选界面右侧 “60Hz” 复选框，可有效抑制电网干扰（适用于北美地区，欧洲用户可调整为 50Hz）。 平滑处理&…...
golang循环变量捕获问题
在 Go 语言中，当在循环中启动协程（goroutine）时，如果在协程闭包中直接引用循环变量，可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下： 问题背景 看这个代码片段： fo…...
shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件： 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...
DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽，大家好，我是左手python！ Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库，用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...
Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中，接口是一种抽象类型，它定义了一组方法的集合： // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的： // 矩形结构体…...
【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...
2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...