算法.图论-习题全集(Updating)
文章目录
- 本节设置的意义
- 并查集篇
- 并查集简介以及常见技巧
- 并查集板子(洛谷)
- 情侣牵手问题
- 相似的字符串组
- 岛屿数量(并查集做法)
- 省份数量
- 移除最多的同行或同列石头
- 最大的人工岛
- 找出知晓秘密的所有专家
- 建图及其拓扑排序篇
- 链式前向星建图板子
- 课程表
本节设置的意义
主要就是为了复习图论算法, 尝试从题目解析的角度,更深入的理解图论算法…
并查集篇
并查集简介以及常见技巧
并查集是一种用于大集团查找, 合并等操作的数据结构, 常见的方法有
find: 用来查找元素在大集团中的代表元素(这里使用的是扁平化的处理)isSameSet: 用来查找两个元素是不是一个大集团的(其实就是find的应用)union: 用来合并两大集团的元素
关于并查集打标签的技巧, 其实我们之前的size数组也是一种打标签的逻辑, 其实打标签就是给每一个集团的代表节点打上标签即可, 还有我们在并查集的题目中通常会设置一个sets作为集合的总数目(每次合并–), 这是一个常见的技巧, 并查集的细节我们在这里不进行过多的介绍, 在之前的章节中有细致的描述…
并查集板子(洛谷)
这里我们的并查集的板子使用的是洛谷的板子(小挂大的优化都没必要其实)
// 并查集模版(洛谷)
// 本实现用递归函数实现路径压缩,而且省掉了小挂大的优化,一般情况下可以省略
// 测试链接 : https://www.luogu.com.cn/problem/P3367import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;public class Main{public static int MAXN = 10001;public static int[] father = new int[MAXN];public static int n;public static void build() {for (int i = 0; i <= n; i++) {father[i] = i;}}public static int find(int i) {if (i != father[i]) {father[i] = find(father[i]);}return father[i];}public static boolean isSameSet(int x, int y) {return find(x) == find(y);}public static void union(int x, int y) {father[find(x)] = find(y);}public static void main(String[] args) throws IOException {BufferedReader br = new BufferedReader(new InputStreamReader(System.in));StreamTokenizer in = new StreamTokenizer(br);PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));while (in.nextToken() != StreamTokenizer.TT_EOF) {n = (int) in.nval;build();in.nextToken();int m = (int) in.nval;for (int i = 0; i < m; i++) {in.nextToken();int z = (int) in.nval;in.nextToken();int x = (int) in.nval;in.nextToken();int y = (int) in.nval;if (z == 1) {union(x, y);} else {out.println(isSameSet(x, y) ? "Y" : "N");}}}out.flush();out.close();br.close();}}情侣牵手问题

本题的突破点就是如果一个大集团里面有 n 对情侣, 那么我们至少要交换 n - 1次(通过把情侣进行编号)
// 这次我们尝试使用轻量版的并查集来解决这道题
class Solution {private static final int MAX_CP = 31;private static final int[] father = new int[MAX_CP];private static int sets = 0;private static int find(int i) {if (i != father[i]) {father[i] = find(father[i]);}return father[i];}private static boolean isSameSet(int a, int b) {return find(a) == find(b);}private static void union(int a, int b) {int fa = find(a);int fb = find(b);if (fa != fb) {father[fa] = fb;sets--;}}// 初始化并查集private static void build(int n) {for (int i = 0; i < n; i++) {father[i] = i;}sets = n;}public int minSwapsCouples(int[] row) {build(row.length / 2);for (int i = 0; i < row.length; i += 2) {int n1 = row[i] / 2;int n2 = row[i + 1] / 2;union(n1, n2);}return row.length / 2 - sets;}
}
相似的字符串组

其实就是枚举每一个位置, 然后判断是不是一组的就OK了
// 还是使用一下轻量级的并查集板子
class Solution {private static final int MAX_SZ = 301;private static final int[] father = new int[MAX_SZ];private static int sets = 0;private static int find(int i) {if (i != father[i]) {father[i] = find(father[i]);}return father[i];}private static boolean isSameSet(int a, int b) {return find(a) == find(b);}private static void union(int a, int b) {int fa = find(a);int fb = find(b);if (fa != fb) {father[fa] = fb;sets--;}}// 初始化并查集private static void build(int n) {for (int i = 0; i < n; i++) {father[i] = i;}sets = n;}public int numSimilarGroups(String[] strs) {build(strs.length);// 主流程的时间复杂度是 O(n ^ 2), 遍历strs的每一个位置int m = strs[0].length();for (int i = 0; i < strs.length; i++) {for (int j = i + 1; j < strs.length; j++) {// 获取到两个字符串, 然后计算两个字符串的不同字符数量String s1 = strs[i];String s2 = strs[j];int diff = 0;for (int k = 0; k < m && diff < 3; k++) {if (s1.charAt(k) != s2.charAt(k))diff++;}if (diff == 0 || diff == 2)union(i, j);}}return sets;}
}
岛屿数量(并查集做法)

这道题的解法非常多, 比如多源 BFS , 洪水填充(其实就是递归加回溯) , 还有今天介绍的并查集的方法(这个方法不是最好的)
// 这个题的并查集做法只要注意一点就可以了: 把一个二维下标转化为一维下标
class Solution {private static final int MAX_SZ = 301 * 301;private static final int[] father = new int[MAX_SZ];private static int sets = 0;private static int row = 0;private static int col = 0;// 模拟bfs的move数组private static final int[] move = { -1, 0, 1, 0, -1 };private static int find(int i) {if (i != father[i]) {father[i] = find(father[i]);}return father[i];}private static boolean isSameSet(int a, int b) {return find(a) == find(b);}private static void union(int a, int b) {int fa = find(a);int fb = find(b);if (fa != fb) {father[fa] = fb;sets--;}}private static void build(char[][] grid, int rl, int cl) {row = rl;col = cl;sets = 0;for (int i = 0; i < row; i++) {for (int j = 0; j < col; j++) {if (grid[i][j] == '1') {sets++;father[getIndex(i, j)] = getIndex(i, j);}}}}public int numIslands(char[][] grid) {// 初始化并查集并统计 '1' 的数量build(grid, grid.length, grid[0].length);// 遍历grid进行合并for (int i = 0; i < row; i++) {for (int j = 0; j < col; j++) {// 向四个方向扩展if (grid[i][j] == '1') {for (int k = 0; k < 4; k++) {int nx = i + move[k];int ny = j + move[k + 1];if (nx >= 0 && nx < row && ny >= 0 && ny < col && grid[nx][ny] == '1') {union(getIndex(i, j), getIndex(nx, ny));}}}}}return sets;}// 二维下标转一维下标private static int getIndex(int i, int j) {return i * col + j;}
}
省份数量

没什么可说的, 就是一个简单的并查集的思路
class Solution {// 这其实也是一个并查集的题private static final int MAXM = 201;private static final int[] father = new int[MAXM];private static final int[] size = new int[MAXM];private static int sets = 0;private static int find(int i){if(i != father[i]){father[i] = find(father[i]);}return father[i];}private static boolean isSameSet(int a, int b){return find(a) == find(b);}private static void union(int a, int b){if(!isSameSet(a, b)){int fa = find(a);int fb = find(b);if(size[fa] > size[fb]){father[fb] = fa;size[fa] += size[fb];}else{father[fa] = fb;size[fb] += size[fa];}sets--;}}private static void build(int n){for(int i = 0; i < n; i++){father[i] = i;size[i] = 1;}sets = n;}public int findCircleNum(int[][] isConnected) {// 初始化并查集build(isConnected.length);for(int i = 0; i < isConnected.length; i++){int[] info = isConnected[i];for(int j = 0; j < info.length; j++){if(info[j] == 1){union(i, j);}}}return sets;}
}
移除最多的同行或同列石头

其实就是每一个集团最后都会被消成一个元素, 我们中间用哈希表加了一些关于离散化的处理的技巧
// 使用一下轻量版本的并查集加上哈希表进行离散化的操作
class Solution {private static Map<Integer, Integer> rowFirst = new HashMap<>();private static Map<Integer, Integer> colFirst = new HashMap<>();private static final int MAXM = 1001;private static final int[] father = new int[MAXM];private static int sets = 0;private static int find(int i){if(i != father[i]){father[i] = find(father[i]);}return father[i];}private static boolean isSameSet(int a, int b){return find(a) == find(b);}private static void union(int a, int b){int fa = find(a);int fb = find(b);if(fa != fb){father[fa] = fb;sets--;}}// 初始化并查集private static void build(int n){for(int i = 0; i < n; i++){father[i] = i;}sets = n;}public int removeStones(int[][] stones) {// 清空哈希表rowFirst.clear();colFirst.clear();// 初始化并查集build(stones.length);for(int i = 0; i < stones.length; i++){int row = stones[i][0];int col = stones[i][1];if(!rowFirst.containsKey(row)){rowFirst.put(row, i);}else{union(rowFirst.get(row), i);}if(!colFirst.containsKey(col)){colFirst.put(col, i);}else{union(colFirst.get(col), i);}}return stones.length - sets;}}
最大的人工岛

本题注意的点就是, 首先我们二维的矩阵, 想要使用并查集, 需要先把二维的坐标转化为一维的坐标, 然后通过一维的坐标使用并查集, 首先把所有的岛进行合并, 然后来到一个 空位置 , 就尝试向四个方向进行扩展尝试进行岛屿的链接, 最后返回最大的连成一片的岛屿数量即可
/*** 本题我们是采用的并查集(轻量板子)的方法来做* 核心点就是首先使用 并查集 (二维下标转换一维下标) 进行人工岛的合并* 本题需要我们使用size的辅助信息, 因为 size 也相当于打标签的技巧* 然后枚举每一个位置进行岛屿的合并*/
class Solution {private static final int MAX_LEN = 501;private static final int MAX_SIZE = MAX_LEN * MAX_LEN;private static final int[] father = new int[MAX_SIZE];private static final int[] size = new int[MAX_SIZE];private static int len = 0;private static final int[] move = {-1, 0, 1, 0, -1};private static int find(int i){if(i != father[i]){father[i] = find(father[i]);}return father[i];}private static boolean isSameSet(int a, int b){return find(a) == find(b);}private static void union(int a, int b){if(!isSameSet(a, b)){int fa = find(a);int fb = find(b);if(size[fa] > size[fb]){father[fb] = fa;size[fa] += size[fb];}else{father[fa] = fb;size[fb] += size[fa];}}}// 初始化并查集private static void build(int[][] grid){len = grid.length;for(int i = 0; i < len; i++){for(int j = 0; j < len; j++){if(grid[i][j] == 1){int index = getIndex(i, j);father[index] = index;size[index] = 1;}}}}// 二维下标转换为一维下标private static int getIndex(int i, int j){return i * len + j;}public int largestIsland(int[][] grid) {build(grid);int res = 0;// 遍历矩阵进行合并for(int i = 0; i < len; i++){for(int j = 0; j < len; j++){if(grid[i][j] == 1){// 此时向四周进行扩展合并for(int k = 0; k < 4; k++){int nx = i + move[k];int ny = j + move[k + 1];if(nx >= 0 && nx < len && ny >= 0 && ny < len && grid[nx][ny] == 1){union(getIndex(i, j), getIndex(nx, ny));}} // 尝试进行人工岛最大面积的更新res = Math.max(res, size[find(getIndex(i, j))]);}}}// 遍历所有的 0 位置, 尝试向四周进行枚举更新最大值// 创建一个map用来进行去重Set<Integer> set = new HashSet<>();for(int i = 0; i < len; i++){for(int j = 0; j < len; j++){if(grid[i][j] == 0){set.clear();int tempRes = 1;// 向四周进行扩展然后尝试进行岛屿链接for(int k = 0; k < 4; k++){int nx = i + move[k];int ny = j + move[k + 1];if(nx >= 0 && nx < len && ny >= 0 && ny < len && grid[nx][ny] == 1){int f = find(getIndex(nx, ny));if(!set.contains(f)){tempRes += size[f];set.add(f);}}}res = Math.max(res, tempRes); }}}return res;}
}
找出知晓秘密的所有专家

本题我们运用的是一种打标签的技巧, 还有就是注意的是并查集如何进行拆解, 其实就是修改一下father数组的内容, 然后把size数组的值置为1即可
/*** 本题主要就是涉及到并查集的打标签的技巧, 还有如何拆散一个并查集* 首先就是关于并查集打标签: 其实就是给集团领袖节点打上标签信息(类似size数组)* 关于拆散并查集: 其实就是把father数组重新设置为自身, size置为1(如果有的话)*/class Solution {// 并查集轻量化的板子private static final int MAXN = 100001;private static final int[] father = new int[MAXN];private static final boolean[] knowSecrets = new boolean[MAXN];private static int find(int i){if(i != father[i]){father[i] = find(father[i]);}return father[i];}private static boolean isSameSet(int a, int b){return find(a) == find(b);}private static void union(int a, int b){if(!isSameSet(a, b)){father[find(a)] = find(b);}}// 初始化并查集private static void build(int n, int firstPerson){for(int i = 0; i < n; i++){father[i] = i;knowSecrets[i] = false;}// 初始化知道秘密的集团(只需要给领袖节点打上标签就好了)union(0, firstPerson);knowSecrets[0] = true;knowSecrets[firstPerson] = true;}public List<Integer> findAllPeople(int n, int[][] meetings, int firstPerson) {// 首先初始化并查集build(n, firstPerson);// 把meetings进行排序便于处理Arrays.sort(meetings, (a, b) -> a[2] - b[2]);int l = 0;int r = 0;while(l < meetings.length){// 首先把r指针置为l的位置r = l;int tempL = l;// 向右侧扩充(结束的时候r指向的下一个不同的元素的边界位置)while(r < meetings.length && meetings[r][2] == meetings[l][2]){r++;}// 先便利一边并查集进行集合元素的合并while(l < r){union(meetings[l][0], meetings[l][1]);if(isSameSet(0, meetings[l][0])) knowSecrets[meetings[l][0]] = true;if(isSameSet(0, meetings[l][1])) knowSecrets[meetings[l][1]] = true;l++;}// 再次便利一边这个时间点的元素进行集合的拆解l = tempL;while(l < r){if(!isSameSet(meetings[l][0], 0) && !isSameSet(meetings[l][1], 0)){father[meetings[l][0]] = meetings[l][0];father[meetings[l][1]] = meetings[l][1];}l++;}l = r;}// 进行元素的收集List<Integer> res = new ArrayList<>();for(int i = 0; i < n; i++){if(isSameSet(0, i)){res.add(i);}}return res;}
}
建图及其拓扑排序篇
建图的方法有三种, 邻接表, 邻接矩阵, 以及链式前向星, 我们更推荐的是静态空间的链式前向星的建图法, 下面是链式前向星的板子
链式前向星建图板子
/*** 关于大厂笔试以及比赛中的建图方式的测试, 其实就是使用静态的数组空间进行建图* 我们设置 3 / 4 / 5 个静态数组空间* head数组(存储点对应的头边编号), next数组(边对应下一条边的编号), to数组(边去往的点), weight数组(边对应的权值), indegree数组(点对应的入度)* 关于拓扑排序(topoSort), 我们最常用的方法其实就是零入度删除法(使用队列, 必要的时候使用小根堆), 关于是否环化的判断我们使用计数器实现* 下面是我们提供的链式建图的板子, 以及拓扑排序的板子*/public class createGraphByLinkedProStar{// 设置点的最大数量private static final int MAXN = 10001;// 设置边的最大数量private static final int MAXM = 10001;// head数组private static final int[] head = new int[MAXN];// next数组private static final int[] next = new int[MAXM];// to数组private static final int[] to = new int[MAXM];// weight数组private static final int[] weight = new int[MAXM];// indegree数组(统计入度)private static final int[] indegree = new int[MAXN];// cnt统计边的数量private static int cnt = 1;// 添加边的方法(顺便统计入度)private static void addEdge(int u, int v, int w){next[cnt] = head[u];to[cnt] = v;weight[cnt] = w;head[u] = cnt++;indegree[v]++;}// 初始化静态空间(只需要清空head以及indegree数组)然后建图(这里是有向带权图)private static void build(int n, int[][] edges){cnt = 1;for(int i = 0; i <= n; i++){indegree[i] = 0;head[i] = 0;}for(int[] edge : edges){addEdge(edge[0], edge[1], edge[2]);}}// 拓扑排序(topoSort的板子)private static int[] topoSort(int n){// 首先创建一个队列(将来可以作为结果返回)int[] queue = new int[n];int l = 0;int r = 0;// 遍历入度表, 添加所有0入度的点进队列for(int i = 0; i < n; i++){if(indegree[i] == 0){queue[r++] = i;}}// 利用链式前向星的遍历开始跑拓扑排序int elemCnt = 0;while(l < r){int cur = queue[l++];elemCnt++;for(int ei = head[cur]; ei != 0; ei = next[ei]){if(--indegree[to[ei]] == 0){queue[r++] = to[ei];}}}return elemCnt == n ? queue : new int[0];}}
课程表
标准的使用拓扑排序的板子 + 加上链式前向星建图法直接打败 100 %

class Solution {// 设置点的最大数量private static final int MAXN = 10001;// 设置边的最大数量private static final int MAXM = 10001;// head数组private static final int[] head = new int[MAXN];// next数组private static final int[] next = new int[MAXM];// to数组private static final int[] to = new int[MAXM];// indegree数组(统计入度)private static final int[] indegree = new int[MAXN];// cnt统计边的数量private static int cnt = 1;// 添加边的方法(顺便统计入度)private static void addEdge(int u, int v){next[cnt] = head[u];to[cnt] = v;head[u] = cnt++;indegree[v]++;}// 初始化静态空间(只需要清空head以及indegree数组)然后建图(这里是有向带权图)private static void build(int n, int[][] edges){cnt = 1;for(int i = 0; i <= n; i++){indegree[i] = 0;head[i] = 0;}for(int[] edge : edges){addEdge(edge[1], edge[0]);}}// 拓扑排序(topoSort的板子)private static int[] topoSort(int n){// 首先创建一个队列(将来可以作为结果返回)int[] queue = new int[n];int l = 0;int r = 0;// 遍历入度表, 添加所有0入度的点进队列for(int i = 0; i < n; i++){if(indegree[i] == 0){queue[r++] = i;}}// 利用链式前向星的遍历开始跑拓扑排序int elemCnt = 0;while(l < r){int cur = queue[l++];elemCnt++;for(int ei = head[cur]; ei != 0; ei = next[ei]){if(--indegree[to[ei]] == 0){queue[r++] = to[ei];}}}return elemCnt == n ? queue : new int[0];}public int[] findOrder(int numCourses, int[][] prerequisites) {build(numCourses, prerequisites);return topoSort(numCourses);}
}相关文章:

算法.图论-习题全集(Updating)
文章目录 本节设置的意义并查集篇并查集简介以及常见技巧并查集板子(洛谷)情侣牵手问题相似的字符串组岛屿数量(并查集做法)省份数量移除最多的同行或同列石头最大的人工岛找出知晓秘密的所有专家 建图及其拓扑排序篇链式前向星建图板子课程表 本节设置的意义 主要就是为了复习…...

this.$prompt 限制输入长度
this.$prompt(请输入关键词名称, 提示, {confirmButtonText: 确定,cancelButtonText: 取消,inputPattern: /^\d{0,50}$/,inputErrorMessage: 关键词名称长度不能超过50个字符 }).then(({ value }) > {})...

JDBC使用p6spy记录实际执行SQL方法【解决SQL打印两次问题】
p6spy介绍 p6spy 是一个开源的 JDBC 数据源代理工具,主要用于拦截和记录应用程序与数据库之间的所有 SQL 操作,方便开发者进行 SQL 调试、性能监控和问题排查。 p6spy可以打印实际执行的sql,在开发过程中方便调试,和使用框架无关…...

问题: redis-高并发场景下如何保证缓存数据与数据库的最终一致性
在高并发场景下,Redis 通常用作缓存层,与数据库结合使用以提高系统的性能。为了保证缓存数据与数据库的最终一致性,通常采用的有双写机制、缓存失效机制,基于双写机制、缓存失效机制又衍生出来了消息队列、事件驱动架构等 常见机…...

Stable Diffusion核心网络结构——CLIP Text Encoder
🌺系列文章推荐🌺 扩散模型系列文章正在持续的更新,更新节奏如下,先更新SD模型讲解,再更新相关的微调方法文章,敬请期待!!!(本文及其之前的文章均已更新&…...

C语言-11-18笔记
1.C语言数据类型 类型存储大小值范围char1 字节-128 到 127 或 0 到 255unsigned char1 字节0 到 255signed char1 字节-128 到 127int2 或 4 字节-32,768 到 32,767 或 -2,147,483,648 到 2,147,483,647unsigned int2 或 4 字节0 到 65,535 或 0 到 4,294,967,295short2 字节…...

数据结构_图的遍历
深度优先搜索遍历 遍历思想 邻接矩阵上的遍历算法 void Map::DFSTraverse() {int i, v;for (i 0; i < MaxLen; i){visited[i] false;}for (i 0; i < Vexnum; i){// 如果顶点未访问,则进行深度优先搜索if (visited[i] false){DFS(i);}}cout << endl…...

设计LRU缓存
LRU缓存 LRU缓存的实现思路LRU缓存的操作C11 STL实现LRU缓存自行设计双向链表 哈希表 LRU(Least Recently Used,最近最少使用)缓存是一种常见的缓存淘汰算法,其基本思想是:当缓存空间已满时,移除最近最少使…...

python中的base64使用小笑话
在使用base64的时候将本地的图片转换为base64 代码如下,代码绝对正确 import base64 def image_to_data_uri(image_path):with open(image_path, rb) as image_file:image_data base64.b64encode(image_file.read()).decode(utf-8)file_extension image_path.sp…...

Python之time时间库
time时间库 概述获取当前时间time库datetime库区别 时间元组处理获取时间元组的各个部分时间戳和时间元组的转换 格式化时间格式化时间解析时间格式符号说明 暂停程序计时操作简单计时高精度计时计时器类的实现 UTC时间操作time库datetime库 概述 time是Python标准库中的一个模…...

Easyexcel(4-模板文件)
相关文章链接 Easyexcel(1-注解使用)Easyexcel(2-文件读取)Easyexcel(3-文件导出)Easyexcel(4-模板文件) 文件导出 获取 resources 目录下的文件,使用 withTemplate 获…...

国产linux系统(银河麒麟,统信uos)使用 PageOffice 动态生成word文件
PageOffice 国产版 :支持信创系统,支持银河麒麟V10和统信UOS,支持X86(intel、兆芯、海光等)、ARM(飞腾、鲲鹏、麒麟等)、龙芯(LoogArch)芯片架构。 数据区域填充文本 数…...

Window11+annie 视频下载器安装
一、ffmpeg环境的配置 下载annie之前需要先配置ffmpeg视频解码器。 网址下载地址 https://ffmpeg.org/download.html1、在网址中选择window版本 2、点击后选择该版本 3、下载完成后对压缩包进行解压,后进行环境的配置 (1)压缩包解压&#…...
配置篇(七))
SAP GR(Group Reporting)配置篇(七)
1.7、合并处理的配置 1.7.1 定义方法 菜单路径 组报表的SAP S4HANA >合并处理的配置>定义方法 事务代码 SPI4...

共建智能软件开发联合实验室,怿星科技助力东风柳汽加速智能化技术创新
11月14日,以“奋进70载,智创新纪元”为主题的2024东风柳汽第二届科技周在柳州盛大开幕,吸引了来自全国的汽车行业嘉宾、技术专家齐聚一堂,共襄盛举,一同探寻如何凭借 “新技术、新实力” 这一关键契机,为新…...
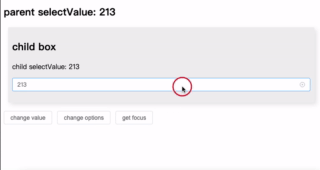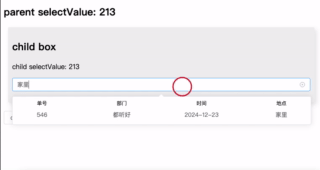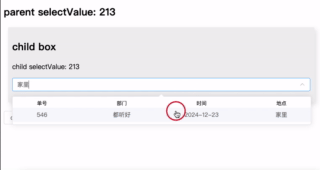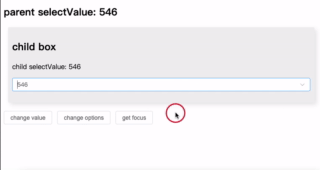
优化表单交互:在 el-select 组件中嵌入表格显示选项
介绍了一种通过 el-select 插槽实现表格样式数据展示的方案,可更直观地辅助用户选择。支持列配置、行数据绑定及自定义搜索,简洁高效,适用于复杂选择场景。完整代码见GitHub 仓库。 背景 在进行业务开发选择订单时,如果单纯的根…...

每日一题 LCR 079. 子集
LCR 079. 子集 主要应该考虑遍历的顺序 class Solution { public:vector<vector<int>> subsets(vector<int>& nums) {vector<vector<int>> ans;vector<int> temp;dfs(nums,0,temp,ans);return ans;}void dfs(vector<int> &…...

cocos creator 3.8 Node学习 3
//在Ts、js中 this指向当前的这个组件实例 //this下的一个数据成员node,指向组件实例化的这个节点 //同样也可以根据节点找到挂载的所有组件 //this.node 指向当前脚本挂载的节点//子节点与父节点的关系 // Node.parent是一个Node,Node.children是一个Node[] // th…...

微信小程序底部button,小米手机偶现布局错误的bug
预期结果:某button fixed 到页面底部,进入该页面时,正常显示button 实际结果:小米13pro,首次进入页面,button不显示。再次进入时,则正常展示 左侧为小米手机第一次进入。 遇到bug的解决思路&am…...

【计组】复习题
冯诺依曼型计算机的主要设计思想是什么?它包括哪些主要组成部分? 主要设计思想: ①采用二进制表示数据和指令,指令由操作码和地址码组成。 ②存储程序,程序控制:将程序和数据存放在存储器中,计算…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

WebRTC调研
WebRTC是什么,为什么,如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...
