Diffusion【2】:VAE
系列文章目录
文章目录
- 系列文章目录
- 前言
- 1. Abstract
- 2. Introduction
- 2.1. Motivation
- 2.2. Contribution
- 3. Methods
- 3.1. Problem Scenario
- 3.2. The variational bound
- 3.3. The SGVB estimator and AEVB algorithm
- 3.3.1. Stochastic Gradient Variational Bayes Estimator
- 3.3.2. Auto-Encoding Variational Bayes
- 3.4. The reparameterization trick
- 3.4.1. Trick
- 3.4.2. Example
- 3.4.3. Scope
- 总结
前言
VAE 可以说是最近大热的生成模型的重要基石。本文侧重对论文内容的翻译和一定程度上的解释。若想完全弄懂 VAE 的具体流程和数学公式推导,建议大家移步苏剑林老师的博客。
原论文链接:Auto-Encoding Variational Bayes
原论文链接:苏神博客
1. Abstract
本文主要探讨了在概率模型中处理潜在变量推断的难点。传统方法难以处理以下两种主要情况:
- 后验分布的不可解性:当模型的后验分布无法通过解析或简单的数值方法计算时,标准方法如期望最大化(EM)或常规变分贝叶斯方法可能无法适用。
- 大规模数据处理:面对大规模数据集时,传统的批量优化或采样方法(如MCMC)变得计算代价高昂。
为了解决上述问题,作者提出了 随机梯度变分贝叶斯估计器(SGVB) 和 自动编码变分贝叶斯算法(AEVB):
- SGVB:通过重新参数化的技巧,将随机变量的采样过程转化为可微函数,这样可以使用高效的随机梯度方法进行优化。
- AEVB:结合 SGVB,用一个神经网络训练的识别模型去近似后验分布,从而实现对潜在变量的高效推断和生成模型参数的高效学习。
意义:
- 效率提升:算法规避了传统推断方法的复杂计算,尤其适用于连续潜在变量的模型。
- 多功能性:学习到的识别模型不仅可以进行后验推断,还能用于数据重建、降噪、表示学习和可视化。
2. Introduction
2.1. Motivation
定向概率模型中的推断与学习是一个难题,尤其是当涉及连续潜在变量时:
- 后验分布往往无法直接求解(不可解)。
- 需要优化的目标通常非常复杂,例如在大数据场景中批量优化计算开销高昂。
传统的变分贝叶斯方法(VB)通过用近似分布替代真实后验分布,并优化这一近似分布来解决问题。但这一方法通常依赖解析计算,其适用性受到限制。
2.2. Contribution
本文的主要贡献:
- 提出 SGVB:通过重新参数化,将不可微的随机采样操作替换为可微的操作,从而可以对目标函数求导并优化。
- 提出 AEVB:利用 SGVB 优化一个称为“识别模型”的神经网络,这个模型能够高效地近似后验分布。
- 通过识别模型,可以高效地对每个数据点的潜在变量进行采样推断,而无需依赖传统的复杂方法(如 MCMC)。
- 这种方法既适用于模型参数的优化,也可以生成与原始数据类似的人工数据。
3. Methods
3.1. Problem Scenario
考虑一个数据集 X = { x ( i ) } i = 1 N X = \{ x^{(i)} \}_{i=1}^N X={x(i)}i=1N,包含 N N N 个独立同分布的样本,每个样本 x ( i ) x^{(i)} x(i) 可以是连续或离散的。我们假设数据是通过一个随机过程生成的,该过程涉及一个未观察到的连续随机变量 z z z。生成过程包括两个步骤:
- 先验采样:从某个先验分布 p θ ∗ ( z ) p_{\theta^*}(z) pθ∗(z) 中生成一个潜在变量样本 z ( i ) z^{(i)} z(i)。
- 条件采样:给定 z ( i ) z^{(i)} z(i),从条件分布 p θ ∗ ( x ∣ z ) p_{\theta^*}(x|z) pθ∗(x∣z) 中生成观测数据 x ( i ) x^{(i)} x(i)。
这里, θ ∗ \theta^* θ∗ 表示真实的参数,但我们并不知道它的具体值。我们假设先验分布 p θ ∗ ( z ) p_{\theta^*}(z) pθ∗(z) 和似然函数 p θ ∗ ( x ∣ z ) p_{\theta^*}(x|z) pθ∗(x∣z) 属于参数化的分布族 p θ ( z ) p_{\theta}(z) pθ(z) 和 p θ ( x ∣ z ) p_{\theta}(x|z) pθ(x∣z),并且它们的概率密度函数对于 θ \theta θ 和 z z z 都几乎处处可微。
需要注意的是,这个生成过程的大部分对我们来说是不可见的:真实的参数 θ ∗ \theta^* θ∗ 和潜在变量 z ( i ) z^{(i)} z(i) 都是未知的。
一个关键的地方是,我们并不对边缘概率或后验概率做常见的简化假设。相反,我们感兴趣的是一种通用的算法,即使在以下困难情况下也能高效工作:
- 不可解性:边缘似然 p θ ( x ) = ∫ p θ ( z ) p θ ( x ∣ z ) d z p_{\theta}(x) = \int p_{\theta}(z)p_{\theta}(x|z) \, dz pθ(x)=∫pθ(z)pθ(x∣z)dz 的积分是不可解的(因此我们无法直接计算或对边缘似然求导);真实的后验分布 p θ ( z ∣ x ) = p θ ( x ∣ z ) p θ ( z ) p θ ( x ) p_{\theta}(z|x) = \frac{p_{\theta}(x|z)p_{\theta}(z)}{p_{\theta}(x)} pθ(z∣x)=pθ(x)pθ(x∣z)pθ(z) 也是不可解的(因此无法使用
EM算法);对于任何合理的平均场变分贝叶斯算法所需的积分也是不可解的。这些不可解性在当似然函数 p θ ( x ∣ z ) p_{\theta}(x|z) pθ(x∣z) 稍微复杂一些(例如包含非线性隐藏层的神经网络)时就会出现。 - 大规模数据集:当数据量非常大时,批量优化计算代价太高;我们希望使用小批量甚至单个数据点来更新参数。基于采样的方法,例如 Monte Carlo EM,在这种情况下通常太慢,因为它需要对每个数据点进行昂贵的采样过程。
在上述场景下,我们希望解决以下三个相关问题:
- 模型参数 θ \theta θ 的高效近似最大似然或最大后验估计。参数 θ \theta θ 本身可能是我们感兴趣的对象,例如在分析某个自然过程时。通过估计 θ \theta θ,我们还可以模拟隐藏的随机过程,生成与真实数据类似的人工数据。
- 给定观测数据 x x x 时,对潜在变量 z z z 进行高效的近似后验推断。这对于编码或数据表示任务非常有用。
- 对变量 x x x 进行高效的近似边缘推断。这使我们能够执行各种需要对 x x x 有先验的推断任务,常见的计算机视觉应用包括图像去噪、修复和超分辨率。
数据生成过程:
- 潜在变量采样:每个数据点 x ( i ) x^{(i)} x(i) 都有一个对应的潜在变量 z ( i ) z^{(i)} z(i),从先验分布 p θ ( z ) p_{\theta}(z) pθ(z) 中采样。
- 观测数据生成:给定 z ( i ) z^{(i)} z(i),从条件分布 p θ ( x ∣ z ) p_{\theta}(x|z) pθ(x∣z) 中生成 x ( i ) x^{(i)} x(i)。
未知量:
- 参数 θ ∗ \theta^* θ∗:真实的模型参数,我们希望估计它。
- 潜在变量 z ( i ) z^{(i)} z(i):未观察到的随机变量,我们希望对其进行推断。
挑战:
- 后验分布不可解:由于 p θ ( z ∣ x ) p_{\theta}(z|x) pθ(z∣x) 无法解析求解,传统的
EM算法或变分推断方法无法直接应用。- 大规模数据:需要高效的算法,能够在不牺牲精度的情况下处理大数据量。
为了解决上述问题,我们引入了一个 识别模型(recognition model) q ϕ ( z ∣ x ) q_{\phi}(z|x) qϕ(z∣x):这是对不可解的真实后验 p θ ( z ∣ x ) p_{\theta}(z|x) pθ(z∣x) 的近似。需要注意的是,与平均场变分推断中的近似后验不同,这里的 q ϕ ( z ∣ x ) q_{\phi}(z|x) qϕ(z∣x) 不一定是可分解的,其参数 ϕ \phi ϕ 也不是通过某种封闭形式的期望计算得出的。相反,我们将介绍一种方法,通过学习来联合优化识别模型的参数 ϕ \phi ϕ 和生成模型的参数 θ \theta θ。
引入识别模型 q ϕ ( z ∣ x ) q_{\phi}(z|x) qϕ(z∣x):
- 目的:近似真实的后验分布 p θ ( z ∣ x ) p_{\theta}(z|x) pθ(z∣x)。
- 特点:不像传统的平均场方法,不需要可解析的期望计算。 q ϕ ( z ∣ x ) q_{\phi}(z|x) qϕ(z∣x) 的形式可以更加灵活。
从编码理论的角度来看,未观察到的变量 z z z 可以解释为一个潜在表示或编码。因此,在本文中,我们也将 识别模型 q ϕ ( z ∣ x ) q_{\phi}(z|x) qϕ(z∣x) 称为概率编码器(probabilistic encoder),因为给定一个数据点 x x x,它会生成一个关于可能的 z z z 值的分布(例如高斯分布),这些 z z z 值可能生成了观测数据 x x x。类似地,我们将 p θ ( x ∣ z ) p_{\theta}(x|z) pθ(x∣z) 称为 概率解码器(probabilistic decoder),因为给定一个编码 z z z,它会生成一个关于可能对应的 x x x 值的分布。
编码器和解码器的解释:
- 概率编码器 q ϕ ( z ∣ x ) q_{\phi}(z|x) qϕ(z∣x):给定输入 x x x,输出关于潜在变量 z z z 的分布,即编码过程。
- 概率解码器 p θ ( x ∣ z ) p_{\theta}(x|z) pθ(x∣z):给定潜在变量 z z z,输出关于观测数据 x x x 的分布,即解码过程。
3.2. The variational bound
边缘似然是各数据点边缘似然的总和: log p θ ( x ( 1 ) , ⋯ , x ( N ) ) = ∑ i = 1 N log p θ ( x ( i ) ) \log p_\theta(x^{(1)}, \cdots, x^{(N)}) = \sum_{i=1}^N \log p_\theta(x^{(i)}) logpθ(x(1),⋯,x(N))=∑i=1Nlogpθ(x(i)),其中每个数据点的边缘似然可以重写为:
log p θ ( x ( i ) ) = D K L ( q ϕ ( z ∣ x ( i ) ) ∣ ∣ p θ ( z ∣ x ( i ) ) ) + L ( θ , ϕ ; x ( i ) ) \log p_\theta(x^{(i)}) = D_{\mathrm{KL}}(q_\phi(z|x^{(i)}) || p_\theta(z|x^{(i)})) + \mathcal{L}(\theta, \phi; x^{(i)}) logpθ(x(i))=DKL(qϕ(z∣x(i))∣∣pθ(z∣x(i)))+L(θ,ϕ;x(i))
公式右侧的第一项是近似后验分布 q ϕ ( z ∣ x ( i ) ) q_\phi(z|x^{(i)}) qϕ(z∣x(i)) 与真实后验分布 p θ ( z ∣ x ( i ) ) p_\theta(z|x^{(i)}) pθ(z∣x(i)) 的 KL 散度,由于 KL 散度非负,因此第二项 L ( θ , ϕ ; x ( i ) ) \mathcal{L}(\theta, \phi; x^{(i)}) L(θ,ϕ;x(i)) 被称为数据点 i i i 的边缘似然的 变分下界,其定义为:
L ( θ , ϕ ; x ( i ) ) = E q ϕ ( z ∣ x ) [ − log q ϕ ( z ∣ x ) + log p θ ( x , z ) ] \mathcal{L}(\theta, \phi; x^{(i)}) = \mathbb{E}{q_\phi(z|x)} [-\log q_\phi(z|x) + \log p_\theta(x, z)] L(θ,ϕ;x(i))=Eqϕ(z∣x)[−logqϕ(z∣x)+logpθ(x,z)]
也可以重写为:
L ( θ , ϕ ; x ( i ) ) = − D K L ( q ϕ ( z ∣ x ( i ) ) ∣ ∣ p θ ( z ) ) + E q ϕ ( z ∣ x ( i ) ) [ log p θ ( x ( i ) ∣ z ) ] \mathcal{L}(\theta, \phi; x^{(i)}) = - D_{\mathrm{KL}}(q_\phi(z|x^{(i)}) || p_\theta(z)) + \mathbb{E}{q_\phi(z|x^{(i)})} [\log p_\theta(x^{(i)}|z)] L(θ,ϕ;x(i))=−DKL(qϕ(z∣x(i))∣∣pθ(z))+Eqϕ(z∣x(i))[logpθ(x(i)∣z)]
我们希望对变分参数 ϕ \phi ϕ 和生成参数 θ \theta θ 同时优化变分下界 L ( θ , ϕ ; x ( i ) ) \mathcal{L}(\theta, \phi; x^{(i)}) L(θ,ϕ;x(i))
边缘似然分解:
- 数据点的边缘似然 log p θ ( x ( i ) ) \log p_\theta(x^{(i)}) logpθ(x(i)) 被分解为两部分:
- KL 散度 D K L ( q ϕ ( z ∣ x ( i ) ) ∣ ∣ p θ ( z ∣ x ( i ) ) ) D_{\mathrm{KL}}(q_\phi(z|x^{(i)}) || p_\theta(z|x^{(i)})) DKL(qϕ(z∣x(i))∣∣pθ(z∣x(i)))。
- 变分下界 L ( θ , ϕ ; x ( i ) ) \mathcal{L}(\theta, \phi; x^{(i)}) L(θ,ϕ;x(i))。
变分下界的意义:
- 由于 KL 散度非负,变分下界 L ( θ , ϕ ; x ( i ) ) \mathcal{L}(\theta, \phi; x^{(i)}) L(θ,ϕ;x(i)) 是边缘似然的下界。
- 优化变分下界可以间接提高边缘似然的值。
下界的分解:
- 第一项是 KL 散度 D K L ( q ϕ ( z ∣ x ( i ) ) ∣ ∣ p θ ( z ) ) D_{\mathrm{KL}}(q_\phi(z|x^{(i)}) || p_\theta(z)) DKL(qϕ(z∣x(i))∣∣pθ(z)),用来衡量近似后验 q_\phi(z|x) 与先验 p θ ( z ) p_\theta(z) pθ(z) 的相似度。
- 第二项是重构误差的期望 E q ϕ ( z ∣ x ( i ) ) [ log p θ ( x ( i ) ∣ z ) ] \mathbb{E}{q_\phi(z|x^{(i)})} [\log p_\theta(x^{(i)}|z)] Eqϕ(z∣x(i))[logpθ(x(i)∣z)],表示生成模型 p θ ( x ∣ z ) p_\theta(x|z) pθ(x∣z) 重构数据的能力。
3.3. The SGVB estimator and AEVB algorithm
3.3.1. Stochastic Gradient Variational Bayes Estimator
在这一节中,我们提出了一种实用的下界及其梯度估计器,并假设近似后验为 q ϕ ( z ∣ x ) q_\phi(z|x) qϕ(z∣x)。需要注意的是,这一技术同样适用于非条件情况下的近似后验 q ϕ ( z ) q_\phi(z) qϕ(z)。
在选定的近似后验分布 q ϕ ( z ∣ x ) q_\phi(z|x) qϕ(z∣x) 的基础上,在一些轻微约束条件下,我们可以通过一个辅助噪声变量 ε \varepsilon ε 的可微变换 g ϕ ( ε , x ) g_\phi(\varepsilon, x) gϕ(ε,x) 对随机变量 z z z 进行重新参数化:
z = g ϕ ( ε , x ) , ε ∼ p ( ε ) z = g_\phi(\varepsilon, x), \quad \varepsilon \sim p(\varepsilon) z=gϕ(ε,x),ε∼p(ε)
对于任何关于 z z z 的函数 f ( z ) f(z) f(z),可以通过以下公式用 ε \varepsilon ε 表达期望值:
E q ϕ ( z ∣ x ) [ f ( z ) ] = E p ( ε ) [ f ( g ϕ ( ε , x ) ) ] \mathbb{E}{q_\phi(z|x)} [f(z)] = \mathbb{E}{p(\varepsilon)} [f(g_\phi(\varepsilon, x))] Eqϕ(z∣x)[f(z)]=Ep(ε)[f(gϕ(ε,x))]
通过蒙特卡罗采样估计:
E q ϕ ( z ∣ x ) [ f ( z ) ] ≈ 1 L ∑ l = 1 L f ( g ϕ ( ε ( l ) , x ) ) \mathbb{E}{q_\phi(z|x)} [f(z)] \approx \frac{1}{L} \sum_{l=1}^L f(g_\phi(\varepsilon^{(l)}, x)) Eqϕ(z∣x)[f(z)]≈L1∑l=1Lf(gϕ(ε(l),x))
其中 ε ( l ) ∼ p ( ε ) \varepsilon^{(l)} \sim p(\varepsilon) ε(l)∼p(ε)。
应用于变分下界,可以得到通用的随机梯度变分贝叶斯(SGVB)估计器:
L ~ A ( θ , ϕ ; x ( i ) ) ≈ 1 L ∑ l = 1 L [ log p θ ( x ( i ) , z ( i , l ) ) − log q ϕ ( z ( i , l ) ∣ x ( i ) ) ] \tilde{\mathcal{L}}A(\theta, \phi; x^{(i)}) \approx \frac{1}{L} \sum{l=1}^L \big[ \log p_\theta(x^{(i)}, z^{(i, l)}) - \log q_\phi(z^{(i, l)}|x^{(i)}) \big] L~A(θ,ϕ;x(i))≈L1∑l=1L[logpθ(x(i),z(i,l))−logqϕ(z(i,l)∣x(i))]
对于某些情况(例如 KL 散度可以解析求解),SGVB 估计器可以被简化为更低方差的形式:
L ~ B ( θ , ϕ ; x ( i ) ) = − D K L ( q ϕ ( z ∣ x ( i ) ) ∣ ∣ p θ ( z ) ) + 1 L ∑ l = 1 L log p θ ( x ( i ) ∣ z ( i , l ) ) \tilde{\mathcal{L}}B(\theta, \phi; x^{(i)}) = - D{\mathrm{KL}}(q_\phi(z|x^{(i)}) || p_\theta(z)) + \frac{1}{L} \sum_{l=1}^L \log p_\theta(x^{(i)}|z^{(i, l)}) L~B(θ,ϕ;x(i))=−DKL(qϕ(z∣x(i))∣∣pθ(z))+L1∑l=1Llogpθ(x(i)∣z(i,l))
其中 z ( i , l ) = g ϕ ( ε ( i , l ) , x ( i ) ) z^{(i, l)} = g_\phi(\varepsilon^{(i, l)}, x^{(i)}) z(i,l)=gϕ(ε(i,l),x(i)),且 ε ( l ) ∼ p ( ε ) \varepsilon^{(l)} \sim p(\varepsilon) ε(l)∼p(ε)。
SGVB的核心是利用 重新参数化技巧,将原始需要对 q ϕ ( z ∣ x ) q_\phi(z|x) qϕ(z∣x) 的积分替换为对辅助噪声变量 ε \varepsilon ε 的积分。这种重新参数化使得:
- 随机变量 z 由噪声变量 \varepsilon 和输入 x 通过可微函数 g_\phi 确定。
- 可以直接通过采样 \varepsilon 来估计目标函数的梯度。
相比传统蒙特卡罗方法,SGVB估计器有以下优点:
- 梯度可微,可以使用高效的优化算法。
- 在某些情况下(如KL散度可解析求解),可以进一步降低方差。
3.3.2. Auto-Encoding Variational Bayes
在独立同分布(i.i.d.)数据集 X X X 的情况下,针对整个数据集的变分下界可以通过小批量(minibatch)估计器进行计算:
L ( θ , ϕ ; X ) ≈ L ~ M ( θ , ϕ ; X M ) = N M ∑ i = 1 M L ~ ( θ , ϕ ; x ( i ) ) \mathcal{L}(\theta, \phi; X) \approx \tilde{\mathcal{L}}M(\theta, \phi; X_M) = \frac{N}{M} \sum{i=1}^M \tilde{\mathcal{L}}(\theta, \phi; x^{(i)}) L(θ,ϕ;X)≈L~M(θ,ϕ;XM)=MN∑i=1ML~(θ,ϕ;x(i))
其中, X M = { x ( i ) } i = 1 M X_M = \{x^{(i)}\}_{i=1}^M XM={x(i)}i=1M 是从完整数据集随机抽取的小批量样本
AEVB结合了SGVB估计器和小批量随机梯度方法,用于优化变分下界。其主要创新点包括:
- 通过小批量样本提高了大数据集上的训练效率。
- 将近似后验建模为神经网络(即识别模型),可以高效地进行推断。
- 使用简单的采样(无需复杂的MCMC),直接进行参数优化。
AEVB的意义
- 效率高:针对大规模数据集,能够以小批量方式快速优化模型参数。
- 灵活性强:可以适配各种含连续潜在变量的生成模型。

算法步骤如下:
- 随机初始化参数 θ , ϕ \theta, \phi θ,ϕ。
- 在每次迭代中:
- 从完整数据集中随机抽取一个小批量 X M X_M XM。
- 从噪声分布 p ( ε ) p(\varepsilon) p(ε) 中采样随机变量 ε \varepsilon ε。
- 计算小批量估计器的梯度 ∇ θ , ϕ L ~ M ( θ , ϕ ; X M , ε ) \nabla_{\theta, \phi} \tilde{\mathcal{L}}_M(\theta, \phi; X_M, \varepsilon) ∇θ,ϕL~M(θ,ϕ;XM,ε)。
- 使用梯度更新参数(例如通过随机梯度下降或 Adagrad 优化器)。
- 重复直至收敛。
3.4. The reparameterization trick
3.4.1. Trick
为了解决我们的问题,提出了一种替代方法来从 q ϕ ( z ∣ x ) q_\phi(z|x) qϕ(z∣x) 中生成样本。重新参数化的核心思想非常简单。假设 z z z 是一个连续随机变量,且 z ∼ q ϕ ( z ∣ x ) z \sim q_\phi(z|x) z∼qϕ(z∣x) 是某个条件分布。那么,通常可以将随机变量 z z z 表示为一个确定性的变量:
z = g ϕ ( ε , x ) z = g_\phi(\varepsilon, x) z=gϕ(ε,x)
其中, ε \varepsilon ε 是一个具有独立边缘分布 p ( ε ) p(\varepsilon) p(ε) 的辅助变量,而 g ϕ ( ⋅ ) g_\phi(\cdot) gϕ(⋅) 是某个参数化的向量值函数。
这种重新参数化对我们的情况非常有用,因为它可以将关于 q ϕ ( z ∣ x ) q_\phi(z|x) qϕ(z∣x) 的期望重写为关于 p ( ε ) p(\varepsilon) p(ε) 的期望,从而使得期望的蒙特卡罗估计对 ϕ \phi ϕ 是可微的。证明如下:
给定确定性映射 z = g ϕ ( ε , x ) z = g_\phi(\varepsilon, x) z=gϕ(ε,x),我们知道 q ϕ ( z ∣ x ) ∏ i d z i = p ( ε ) ∏ i d ε i q_\phi(z|x) \prod_i dz_i = p(\varepsilon) \prod_i d\varepsilon_i qϕ(z∣x)∏idzi=p(ε)∏idεi。因此:
∫ q ϕ ( z ∣ x ) f ( z ) d z = ∫ p ( ε ) f ( g ϕ ( ε , x ) ) d ε \int q_\phi(z|x) f(z) dz = \int p(\varepsilon) f(g_\phi(\varepsilon, x)) d\varepsilon ∫qϕ(z∣x)f(z)dz=∫p(ε)f(gϕ(ε,x))dε
这表明可以构造一个可微的估计器:
∫ q ϕ ( z ∣ x ) f ( z ) d z ≈ 1 L ∑ l = 1 L f ( g ϕ ( x , ε ( l ) ) ) \int q_\phi(z|x) f(z) dz \approx \frac{1}{L} \sum_{l=1}^L f(g_\phi(x, \varepsilon^{(l)})) ∫qϕ(z∣x)f(z)dz≈L1∑l=1Lf(gϕ(x,ε(l)))
其中 ε ( l ) ∼ p ( ε ) \varepsilon^{(l)} \sim p(\varepsilon) ε(l)∼p(ε)。
重新参数化的作用
- 将随机性移到辅助变量 \varepsilon:
原始的 z z z 依赖于复杂的后验分布 q ϕ ( z ∣ x ) q_\phi(z|x) qϕ(z∣x),直接优化非常困难。重新参数化将 z z z 表示为由可控参数 ϕ \phi ϕ、输入 x x x 和简单分布 p ( ε ) p(\varepsilon) p(ε) 生成的确定性变量,从而简化了采样和优化。- 使梯度计算成为可能:
原始的采样过程通常不可微,但通过重新参数化,可以将目标函数关于 ϕ \phi ϕ 的梯度转化为辅助变量 ε \varepsilon ε 的期望,这种期望是可微的。- 简化变分推断:
在变分推断中,我们需要优化变分下界(涉及关于 q ϕ ( z ∣ x ) q_\phi(z|x) qϕ(z∣x) 的积分)。重新参数化技巧有效地将积分转化为简单分布 p ( ε ) p(\varepsilon) p(ε) 的采样问题,降低了计算复杂度。
3.4.2. Example
以单变量高斯分布为例:假设 z ∼ q ( z ∣ x ) = N ( μ , σ 2 ) z \sim q(z|x) = \mathcal{N}(\mu, \sigma^2) z∼q(z∣x)=N(μ,σ2)。在这种情况下,一个有效的重新参数化是:
z = μ + σ ε , ε ∼ N ( 0 , 1 ) z = \mu + \sigma \varepsilon, \quad \varepsilon \sim \mathcal{N}(0, 1) z=μ+σε,ε∼N(0,1)
因此:
E N ( z ; μ , σ 2 ) [ f ( z ) ] = E N ( ε ; 0 , 1 ) [ f ( μ + σ ε ) ] ≈ 1 L ∑ l = 1 L f ( μ + σ ε ( l ) ) \mathbb{E}{\mathcal{N}(z; \mu, \sigma^2)}[f(z)] = \mathbb{E}{\mathcal{N}(\varepsilon; 0, 1)}[f(\mu + \sigma \varepsilon)] \approx \frac{1}{L} \sum_{l=1}^L f(\mu + \sigma \varepsilon^{(l)}) EN(z;μ,σ2)[f(z)]=EN(ε;0,1)[f(μ+σε)]≈L1∑l=1Lf(μ+σε(l))
其中 ε ( l ) ∼ N ( 0 , 1 ) \varepsilon^{(l)} \sim \mathcal{N}(0, 1) ε(l)∼N(0,1)。
在高斯分布中,重新参数化技巧将采样过程分解为简单的均值和标准差调整:
- 均值 μ \mu μ 控制生成的中心位置。
- 标准差 σ \sigma σ 控制生成的随机性。
通过引入标准正态分布的噪声 ε \varepsilon ε,采样过程变得简单且可微。
3.4.3. Scope
对于哪些 q ϕ ( z ∣ x ) q_\phi(z|x) qϕ(z∣x),我们可以选择这种可微变换 g ϕ ( ⋅ ) g_\phi(\cdot) gϕ(⋅) 和辅助变量 ε ∼ p ( ε ) \varepsilon \sim p(\varepsilon) ε∼p(ε)。以下三种基本方法可行:
- 可逆累计分布函数(CDF):
如果分布的逆CDF是可求的,可以令 ε ∼ U ( 0 , 1 ) \varepsilon \sim U(0, 1) ε∼U(0,1),并令 g ϕ ( ε , x ) g_\phi(\varepsilon, x) gϕ(ε,x) 为分布 q ϕ ( z ∣ x ) q_\phi(z|x) qϕ(z∣x) 的逆CDF。例如:指数分布、洛伦兹分布(Cauchy)、对数正态分布等。 - 位置-尺度分布:
对于任何“位置-尺度”分布族,可以选择标准分布(位置=0,尺度=1)作为辅助变量 ε \varepsilon ε,并定义 g ( ⋅ ) = 位置 + 尺度 ⋅ ε g(\cdot) = \text{位置} + \text{尺度} \cdot \varepsilon g(⋅)=位置+尺度⋅ε。例如:高斯分布、拉普拉斯分布、学生 t 分布等。 - 组合变换:
一些复杂分布可以通过辅助变量的多种变换表达。例如:- 对数正态分布:通过指数化正态分布的变量得到。
- Gamma分布:通过指数分布变量的加和得到。
- Dirichlet分布:通过加权的Gamma分布变量得到。
总结
Auto-Encoding Variational Bayes (AEVB) 提出了一个高效的框架,将传统变分推断与深度学习结合,为潜变量模型的训练与推断提供了一种自动化的方法。通过 重参数化技巧 和 证据下界(ELBO) 的优化,该方法解决了复杂后验分布的推断问题,并实现了生成建模的高效优化。AEVB 的思想奠定了 变分自编码器(VAE) 的基础,极大地推动了生成模型领域的发展。
相关文章:

Diffusion【2】:VAE
系列文章目录 文章目录 系列文章目录前言1. Abstract2. Introduction2.1. Motivation2.2. Contribution 3. Methods3.1. Problem Scenario3.2. The variational bound3.3. The SGVB estimator and AEVB algorithm3.3.1. Stochastic Gradient Variational Bayes Estimator3.3.2.…...

高级java每日一道面试题-2024年11月19日-基本篇-获取一个类Class对象的方式有哪些?
如果有遗漏,评论区告诉我进行补充 面试官: 获取一个类Class对象的方式有哪些? 我回答: 在 Java 中,获取一个类的 Class 对象有多种方式。这些方式各有优缺点,适用于不同的场景。以下是常见的几种方法及其详细解释: 1. 使用 new 关键字实…...

xilinx xapp1171学习笔记
在xapp1171示例中,假设Host PC将PCIE:BAR0赋值为:0x00000000_def00000 PCIEBAR2AXIBAR_00x81000000,即Host PC读写0x00000000_def00000就是在读写AXI地址0x81000000(BRAM在AXI总线上的基地址) 在AXI总线上࿰…...

一次需升级系统的wxpython安装(macOS M1)
WARNING: The scripts libdoc, rebot and robot are installed in /Users/用户名/Library/Python/3.8/bin which is not on PATH. 背景:想在macos安装Robot Framework ,显示pip3不是最新,更新pip3后显示不在PATH上 参看博主文章末尾 MAC系统…...

el-table 数据去重后合并表尾合计行,金额千分位分割并保留两位小数,表尾合计行表格合并
问题背景 最近在做后台管理项目el-table 时候需要进行表尾合计,修改合计后文字的样式,合并单元格。 想实现的效果 合并表尾单元格前三列为1格;对某些指定的单元格进行表尾合计;合计后的文本样式加粗;涉及到金额需要千…...

Springboot整合mybatis-plus使用pageHelper进行分页
PageHelper 使用步骤全解析 在进行 Web 应用开发时,经常会涉及到数据库数据的分页展示。PageHelper 是一个非常实用的 MyBatis 分页插件,它能够方便地实现数据库查询结果的分页功能,极大地提高了开发效率。以下将简单介绍 PageHelper 的使用…...

【Xbim+C#】创建拉伸的墙
基础 基础回顾 效果图 简单的工具类 using System.Collections.Generic; using System.Linq; using Xbim.Common.Step21; using Xbim.Ifc; using Xbim.Ifc4.GeometricConstraintResource; using Xbim.Ifc4.GeometricModelResource; using Xbim.Ifc4.GeometryResource; using…...

【阅读记录-章节3】Build a Large Language Model (From Scratch)
目录 3 Coding attention mechanisms3.1 The problem with modeling long sequences背景:注意力机制的动机 3.2 Capturing data dependencies with attention mechanismsRNN的局限性与改进Transformer架构的革命 3.3 Attending to different parts of the input wit…...

three.js 对 模型使用 视频进行贴图修改材质
three.js 对 模型使用 视频进行贴图修改材质 https://threehub.cn/#/codeMirror?navigationThreeJS&classifyapplication&idvideoModel import * as THREE from three import { OrbitControls } from three/examples/jsm/controls/OrbitControls.js import { GLTFLoad…...

MySQL - 数据库基础 | 数据库操作 | 表操作
文章目录 1、数据库基础1.1为什么要有数据库1.2主流的数据库1.3连接MySQL1.4服务器、数据库、表的关系1.5 MySQL框架1.6 SQL分类1.7储存引擎 2.数据库操作2.1创建数据库2.2字符集和校验规则2.3删除数据库2.4修改数据库2.5备份与恢复2.6查看连接情况 3.表的操作3.1创建表3.2查看…...

maven父子项目
目录 一、创建Maven父子项目 二、父子项目的关联 三、父子项目的继承关系 四、构建父子项目 五、Maven父子项目的优势 Maven父子项目是一种项目结构,它允许一个父项目(也称为根项目)管理多个子项目(也称为模块)。…...
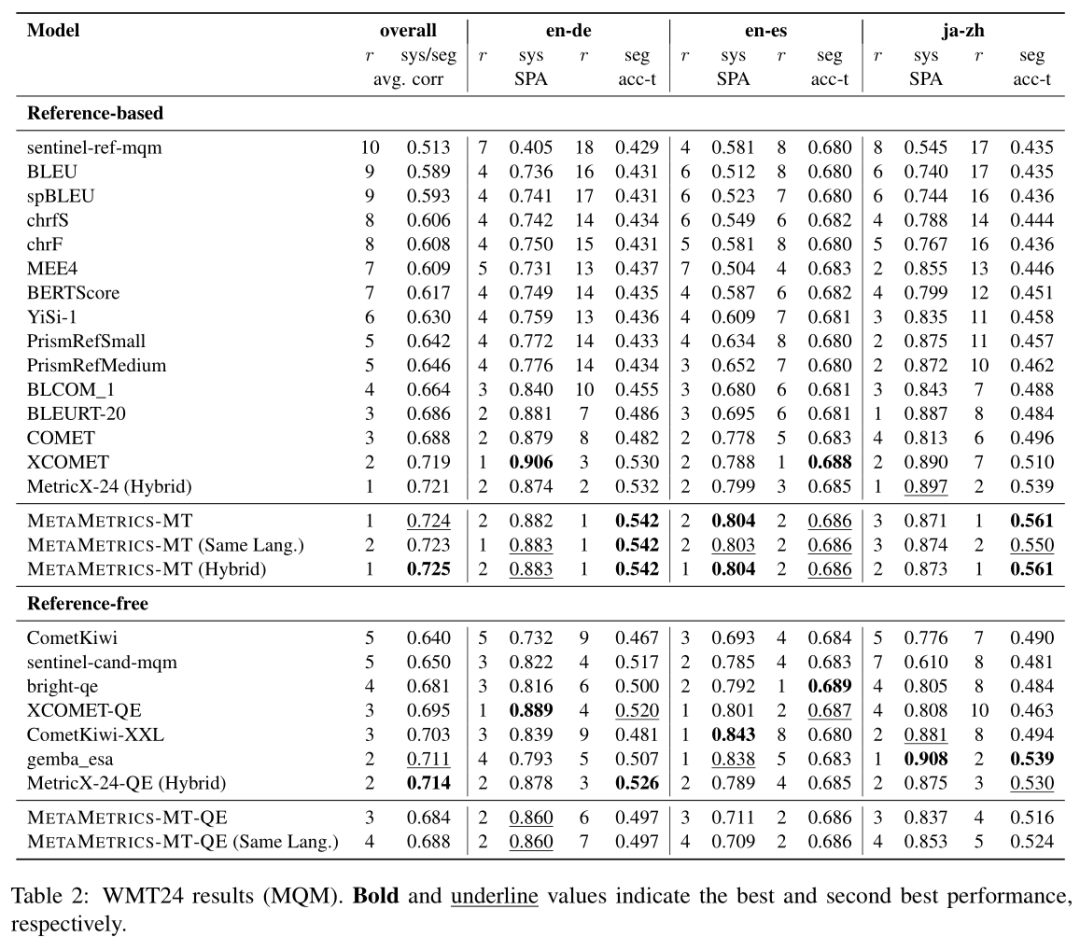
NLP论文速读(多伦多大学)|利用人类偏好校准来调整机器翻译的元指标
论文速读|MetaMetrics-MT: Tuning Meta-Metrics for Machine Translation via Human Preference Calibration 论文信息: 简介: 本文的背景是机器翻译(MT)任务的评估。在机器翻译领域,由于不同场景和语言对的需求差异&a…...
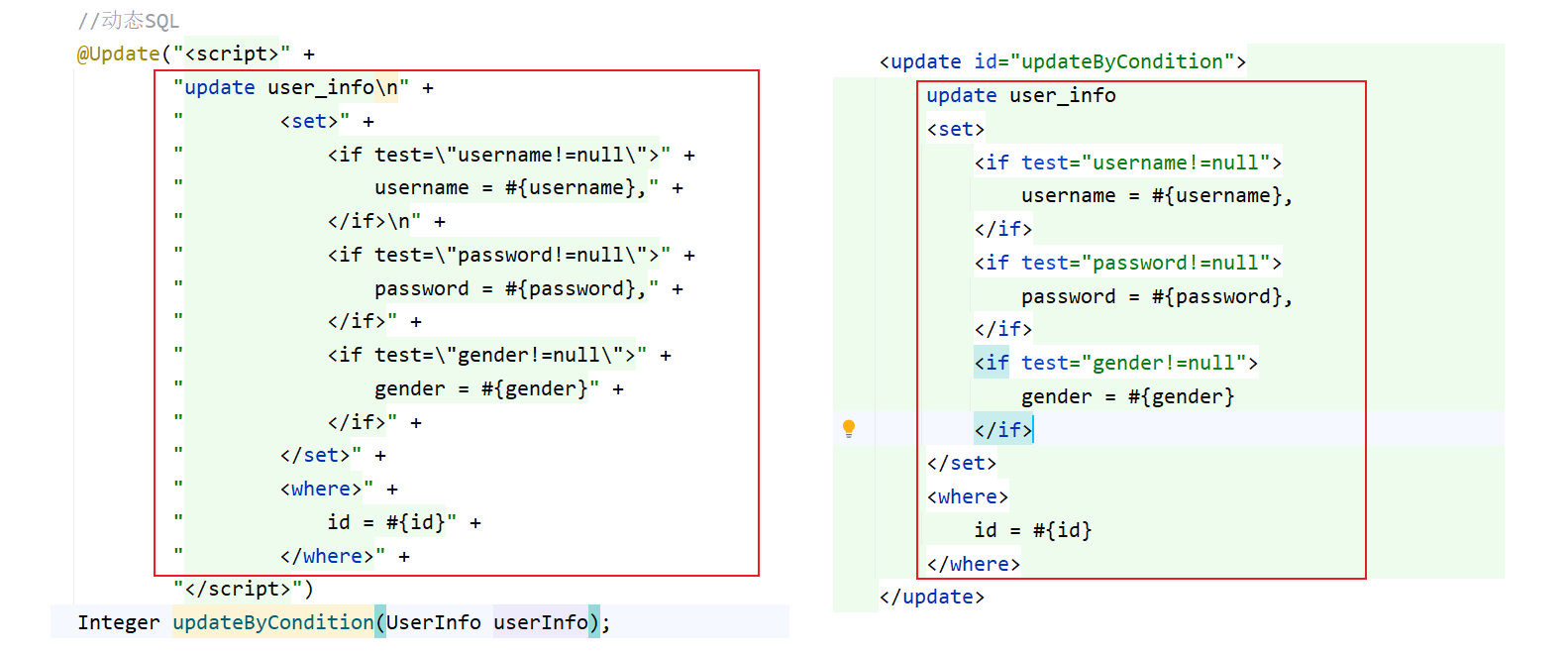
MyBatis——#{} 和 ${} 的区别和动态 SQL
1. #{} 和 ${} 的区别 为了方便,接下来使用注解方式来演示: #{} 的 SQL 语句中的参数是用过 ? 来起到类似于占位符的作用,而 ${} 是直接进行参数替换,这种直接替换的即时 SQL 就可能会出现一个问题 当传入一个字符串时ÿ…...

解决sql字符串
根据你描述的情况以及调试截图中的内容,我可以确认你的 sql 字符串在 Python 中由于转义字符的问题,可能导致在 Oracle 中运行时出错。 以下是一些排查和修改建议: 问题分析 转义字符问题: 在调试界面中可以看到,DEC…...

深度解析:Android APP集成与拉起微信小程序开发全攻略
目录 一、背景以及功能介绍 二、Android开发示例 2.1 下载 SDK 2.2 调用接口 2.3 获取小程序原始Id 2.4 报错提示:bad_param 2.4.1 错误日志 2.4.2 解决方案 相关推荐 一、背景以及功能介绍 需求:产品经理需要APP跳转到公司的小程序(最好指定页…...

Leetcode 被围绕的区域
算法思想(解题思路): 这道题的核心是 将所有被边界包围的 O 保留下来,而将其他被围绕的 O 转换为 X。为了实现这一目标,我们可以分三步完成: 第一步:标记边界及其相连的 O 为特殊标记ÿ…...

ssm框架-spring-spring声明式事务
声明式事务概念 声明式事务是指使用注解或 XML 配置的方式来控制事务的提交和回滚。 开发者只需要添加配置即可, 具体事务的实现由第三方框架实现,避免我们直接进行事务操作! 使用声明式事务可以将事务的控制和业务逻辑分离开来,提…...

React第五节 组件三大属性之 props 用法详解
特性 a、props最好是仅限于父子上下级之间的数据传递,如果是祖孙多级之间传递属性,可以考虑使用props是否合适,或者使用替代方案 useContext() 或者使用 redux状态管理; b、props 中的属性是只读属性,如果想修改其中的…...

测评部署和管理 WordPress 最方便的面板
新版宝塔面板快速搭建WordPress新手教程 - 倚栏听风-Morii - 博客园 初学者使用1Panel面板快速搭建WordPress网站 - 倚栏听风-Morii - 博客园 可以看到,无论是宝塔还是1Panel,部署和管理WordPress都有些繁琐,而且还需要额外去配置Nginx和M…...

【系统分析师】-2024年11月论文-论DevOps开发
1、题目要求 论Devops及其应用。Devops是一组过程、方法与系统的统称,用于促进开发、技术运营和质量保障部门之间的沟通,协作与整合。它是一种重视软体开发人员和工厂运维技术人员之间沟通合作的模式。透过自动化“软件交付”和“架构变更”的流程&…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...
