量子感知机
神经网络类似于人类大脑,是模拟生物神经网络进行信息处理的一种数学模型。它能解决分类、回归等问题,是机器学习的重要组成部分。量子神经网络是将量子理论与神经网络相结合而产生的一种新型计算模式。1995年美国路易斯安那州立大学KAK教授首次提出了量子神经计算的概念,开创了该领域的先河。随后又相继 出现了多种量子神经计算模型,包括量子感知机、量子神经网络、量子受限玻尔兹曼机等。近年来,量子生成对抗网络、量子卷积神经网络等量子机器学习模型。
量子感知机算法,这与经典感知机的方法类似,在量子感知机中,规定输入样本和权重系数w的元素只能为
1。经典感知机中通过激活函数的输出判断输入样本是否被正确分类。而在量子算法中通过阈值
将式写为
(1)
1.的计算方法
,即
和
的内积的模。在量子计算中,样本信息
和权重系数
存储在量子态中,归一化之后,
和
的量子态形式为
(2)
(3)
这里系数取是因为量子算法中
和
内积的模为
。
假设存在酉算子和
能够完成如下变换:
(4)
(5)
式子中:。
则有 ,将
写成十进制的形式有,
。
首先制备初态,其中前m个量子比特用于存储输入样本向量
和权重
,最后一位是辅助量子比特,用于存储最终结果。
第一步:使用酉算子作用于前m个量子比特
,得到量子态
(6)
第二步:使用作用于
得到量子态
(7)
式子中:
则 (8)
#量子感知机
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister, transpile
from qiskit_aer import Aer
import numpy as np
from qiskit.visualization import plot_histogramfrom math import pi
from qiskit.visualization import plot_histogramcircuit = QuantumCircuit(5,5)
#两控制位的受控z门
def ccz():circuit=QuantumCircuit(2)circuit.cz(0,1)circuit= circuit.to_gate()circuit.name = "ccz"c_U = circuit.control()return c_U
#两控制位的受控z门(与前一个的控制位不同)
def ccz1():circuit=QuantumCircuit(3)circuit.cz(0,2)circuit= circuit.to_gate()circuit.name = "ccz1"c_U = circuit.control()return c_U
#三控制位的受控z门
def cccz():circuit=QuantumCircuit(3)circuit.append(ccz(),[0]+[m+1 for m in range(2)])circuit= circuit.to_gate()circuit.name = "cccz"c_U = circuit.control()return c_U
#三控制位的受控x门
def cccx():circuit=QuantumCircuit(3)circuit.ccx(0,1,2)circuit= circuit.to_gate()circuit.name = "cccx"c_U = circuit.control()return c_U
#四控制位的受控x门
def ccccx():circuit=QuantumCircuit(4)circuit.append(cccx(),[0]+[m+1 for m in range(3)])circuit= circuit.to_gate()circuit.name = "ccccx"c_U = circuit.control()return c_U
#U_i
for i in range(4):circuit.h(i)
for i in range(3):circuit.z(i)
circuit.cz(1,2)
circuit.cz(0,2)
circuit.cz(0,1)
circuit.append(ccz(),[0]+[m+1 for m in range(2)])
#U_w
circuit.z(1)
circuit.z(2)
circuit.cz(1,3)
circuit.cz(0,2)
circuit.cz(0,1)
circuit.append(ccz(),[1]+[m+2 for m in range(2)])
circuit.append(ccz1(),[0]+[m+1 for m in range(3)])
circuit.append(cccz(),[0]+[m+1 for m in range(3)])
for i in range(4):circuit.h(i)
for i in range(4):circuit.x(i)
#将内积提取到辅助量子比特上
circuit.append(ccccx(),[0]+[m+1 for m in range(4)])
circuit.barrier()
circuit.measure(4,4)
circuit.draw(output='mpl', plot_barriers=False)
# Set up the backend
backend = Aer.get_backend('qasm_simulator')
# Transpile the circuit for the simulator
transpiled_circuit = transpile(circuit, backend)
# Run the transpiled circuit
job = backend.run(transpiled_circuit, shots=100000)
sim_result = job.result()
# Get and plot the results
measurement_result = sim_result.get_counts(circuit)
plot_histogram(measurement_result)

1的概率为0.1376,开根号为0.370944,小于0.5,属于。
相关文章:
量子感知机
神经网络类似于人类大脑,是模拟生物神经网络进行信息处理的一种数学模型。它能解决分类、回归等问题,是机器学习的重要组成部分。量子神经网络是将量子理论与神经网络相结合而产生的一种新型计算模式。1995年美国路易斯安那州立大学KAK教授首次提出了量子…...
VM虚拟机装MAC后无法联网,如何解决?
✨在vm虚拟机上,给虚拟机MacOS设置网络适配器。选择NAT模式用于共享主机的IP地址 ✨在MacOS设置中设置网络 以太网 使用DHCP ✨回到本地电脑上,打开 服务,找到VMware DHCP和VMware NAT,把这两个服务打开,专一般问题就…...
IDEA 基本设置
设置主题 设置字体 设置编码格式 改变字体大小 开启 按住 ctrl 滚轮 改变字体大小。 开启自动编译...
Chrome 浏览器 131 版本新特性
Chrome 浏览器 131 版本新特性 一、Chrome 浏览器 131 版本更新 1. 在 iOS 上使用 Google Lens 搜索 自 Chrome 126 版本以来,用户可以通过 Google Lens 搜索屏幕上看到的任何图片或文字。 要使用此功能,请访问网站,并点击聚焦时出现在地…...

使用php和Xunsearch提升音乐网站的歌曲搜索效果
文章精选推荐 1 JetBrains Ai assistant 编程工具让你的工作效率翻倍 2 Extra Icons:JetBrains IDE的图标增强神器 3 IDEA插件推荐-SequenceDiagram,自动生成时序图 4 BashSupport Pro 这个ides插件主要是用来干嘛的 ? 5 IDEA必装的插件&…...

计算机毕设-基于springboot的高校网上缴费综合务系统视频的设计与实现(附源码+lw+ppt+开题报告)
博主介绍:✌多个项目实战经验、多个大型网购商城开发经验、在某机构指导学员上千名、专注于本行业领域✌ 技术范围:Java实战项目、Python实战项目、微信小程序/安卓实战项目、爬虫大数据实战项目、Nodejs实战项目、PHP实战项目、.NET实战项目、Golang实战…...
STL关联式容器之map
map的特性是,所有元素都会根据元素的键值自动被排序。map的所有元素都是pair,同时拥有实值(value)和键值(key)。pair的第一元素被视为键值,第二元素被视为实值。map不允许两个元素拥有相同的键值。下面是<stl_pair.h>中pair的定义 tem…...
【HarmonyOS】鸿蒙应用唤起系统相机拍照
【HarmonyOS】鸿蒙应用唤起系统相机拍照 方案一: 官方推荐的方式,使用CameraPicker来调用安全相机进行拍照。 let pathDir getContext().filesDir;let fileName ${new Date().getTime()}let filePath pathDir /${fileName}.tmpfileIo.createRandomA…...

Linux系统使用valgrind分析C++程序内存资源使用情况
内存占用是我们开发的时候需要重点关注的一个问题,我们可以人工根据代码推理出一个消耗内存较大的函数,也可以推理出大概会消耗多少内存,但是这种方法不仅麻烦,而且得到的只是推理的数据,而不是实际的数据。 我们可以…...

Java基础夯实——2.7 线程上下文切换
线程上下文切换(Thread Context Switching)是操作系统在多线程环境中,切换CPU从执行一个线程的上下文到另一个线程的上下文的过程。这种切换是实现多线程并发执行的核心机制之一。 1 上下文: 线程的上下文指线程在某一时刻的执行状态,如&am…...

死锁相关习题 10道 附详解
2022 设系统中有三种类型的资源(A,B,C)和五个进程(P1,P2,P3,P4,P5),A资源的数量是17,B资源的数量是6,C资源的数量是19。在T0时刻系统的状态: 最大资源需求量已分配资源量A,B,CA,B,…...
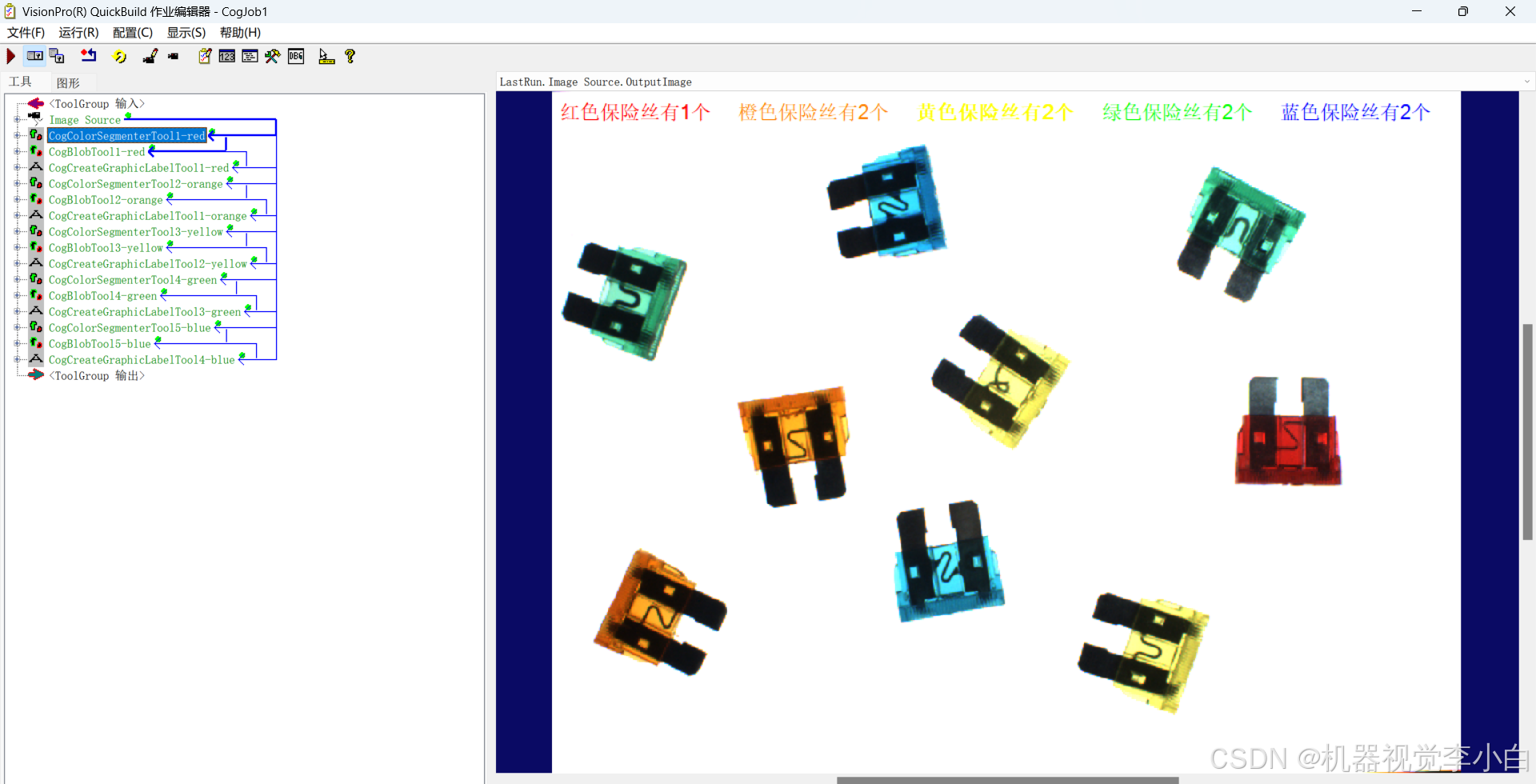
VisionPro 机器视觉案例 之 彩色保险丝个数统计
第十四篇 机器视觉案例 之 彩色保险丝颜色识别个数统计 文章目录 第十四篇 机器视觉案例 之 彩色保险丝颜色识别个数统计1.案例要求2.实现思路2.1 方法一 颜色分离工具CogColorSegmenterTool将每一种颜色分离出来,得到对应的单独图像,使用斑点工具CogBlo…...
go-zero(七) RPC服务和ETCD
go-zero 实现 RPC 服务 在实际的开发中,我们是通过RPC来传递数据的,下面我将通过一个简单的示例,说明如何使用go-zero框架和 Protocol Buffers 定义 RPC 服务。 一、生成 RPC项目 在这个教程中,我们根据user.api文件࿰…...

Jenkins + gitee 自动触发项目拉取部署(Webhook配置)
目录 前言 Generic Webhook Trigger 插件 下载插件 编辑 配置WebHook 生成tocken 总结 前言 前文简单介绍了Jenkins环境搭建,本文主要来介绍一下如何使用 WebHook 触发自动拉取构建项目; Generic Webhook Trigger 插件 实现代码推送后,触…...
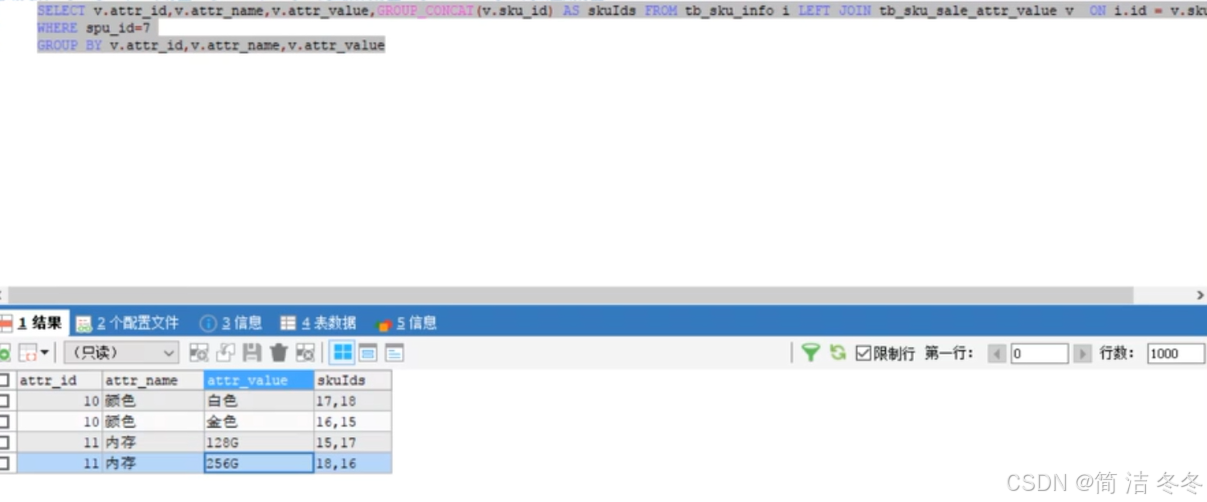
043 商品详情
文章目录 详情页数据表结构voSkuItemVo.javaSkuItemSaleAttrVo.javaAttrValueAndSkuIdVo.javaSpuAttrGroupVo.javaGroupAttrParamVo.java pom.xmlSkuSaleAttrValueDao.xmlSkuSaleAttrValueDao.javaAttrGroupDao.xmlAttrGroupServiceImpl.javaSkuInfoServiceImpl.javaSkuSaleAtt…...

【人工智能】Python与Scikit-learn的模型选择与调参:用GridSearchCV和RandomizedSearchCV提升模型性能
解锁Python编程的无限可能:《奇妙的Python》带你漫游代码世界 在机器学习建模过程中,模型的表现往往取决于参数的选择与优化。Scikit-learn提供了便捷的工具GridSearchCV和RandomizedSearchCV,帮助我们在参数空间中搜索最佳组合以提升模型表现。本文将从理论和实践两个角度…...

深入探讨 Puppeteer 如何使用 X 和 Y 坐标实现鼠标移动
背景介绍 现代爬虫技术中,模拟人类行为已成为绕过反爬虫系统的关键策略之一。无论是模拟用户点击、滚动,还是鼠标的轨迹移动,都可以为爬虫脚本带来更高的“伪装性”。在众多的自动化工具中,Puppeteer作为一个无头浏览器控制库&am…...
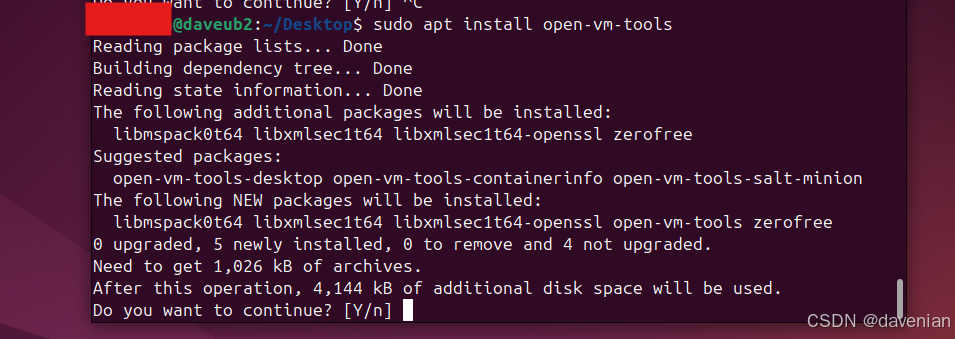
<OS 有关> ubuntu 24 不同版本介绍 安装 Vmware tools
原因 想用 apt-get download 存到本地 / NAS上,减少网络流浪。 看到 VMware 上的确实有 ubuntu,只是版本是16。 ubuntu 版本比较:LTS vs RR LTS: Long-Term Support 长周期支持, 一般每 2 年更新,会更可靠与更稳定…...

C#调用JAVA
参考教程:使用IKVMC转换Jar为dll动态库(含idea打包jar方法)-CSDN博客 已经实践过,好使。...

JavaEE-多线程基础知识
文章目录 前言与回顾创建一个多线程线程的创建以及运行机制简述step1: 继承Thread类step2: 实现Runable接口step3: 基于step1使用匿名内部类step4: 基于step2使用匿名内部类step5: 基于step4使用lambda表达式(推荐) Thread的常见方法关于jconsole监视线程的工具构造方法解析获取…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

React从基础入门到高级实战:React 实战项目 - 项目五:微前端与模块化架构
React 实战项目:微前端与模块化架构 欢迎来到 React 开发教程专栏 的第 30 篇!在前 29 篇文章中,我们从 React 的基础概念逐步深入到高级技巧,涵盖了组件设计、状态管理、路由配置、性能优化和企业级应用等核心内容。这一次&…...

Django RBAC项目后端实战 - 03 DRF权限控制实现
项目背景 在上一篇文章中,我们完成了JWT认证系统的集成。本篇文章将实现基于Redis的RBAC权限控制系统,为系统提供细粒度的权限控制。 开发目标 实现基于Redis的权限缓存机制开发DRF权限控制类实现权限管理API配置权限白名单 前置配置 在开始开发权限…...

RabbitMQ 各类交换机
为什么要用交换机? 交换机用来路由消息。如果直发队列,这个消息就被处理消失了,那别的队列也需要这个消息怎么办?那就要用到交换机 交换机类型 1,fanout:广播 特点 广播所有消息:将消息…...
