【LeetCode每日一题】——746.使用最小花费爬楼梯
文章目录
- 一【题目类别】
- 二【题目难度】
- 三【题目编号】
- 四【题目描述】
- 五【题目示例】
- 六【题目提示】
- 七【解题思路】
- 八【时空频度】
- 九【代码实现】
- 十【提交结果】
一【题目类别】
- 数组
二【题目难度】
- 简单
三【题目编号】
- 746.使用最小花费爬楼梯
四【题目描述】
- 给你一个整数数组
cost,其中cost[i]是从楼梯第i个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。 - 你可以选择从下标为
0或下标为1的台阶开始爬楼梯。 - 请你计算并返回达到楼梯顶部的最低花费。
五【题目示例】
-
示例 1:
- 输入:cost = [10,15,20]
- 输出:15
- 解释:你将从下标为 1 的台阶开始。
- 支付 15 ,向上爬两个台阶,到达楼梯顶部。
- 总花费为 15 。
-
示例 2:
- 输入:cost = [1,100,1,1,1,100,1,1,100,1]
- 输出:6
- 解释:你将从下标为 0 的台阶开始。
- 支付 1 ,向上爬两个台阶,到达下标为 2 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 4 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 6 的台阶。
- 支付 1 ,向上爬一个台阶,到达下标为 7 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 9 的台阶。
- 支付 1 ,向上爬一个台阶,到达楼梯顶部。
- 总花费为 6 。
六【题目提示】
2 <= cost.length <= 10000 <= cost[i] <= 999
七【解题思路】
- 该题为标准的动态规划题目
- 对于第i个位置,cost[i]为第i个位置向上爬的花费,dp[i]为到达第i个位置所需要的最小的花费,所以可以得到动态转移方程:
- dp[i] = min(cost[i - 1] + dp[i - 1], cost[i - 2] + dp[i - 2])
- 最后返回结果即可
- 具体细节可以参考下面的代码
八【时空频度】
- 时间复杂度: O ( n ) O(n) O(n), n n n为传入的数组的长度
- 空间复杂度: O ( n ) O(n) O(n), n n n为传入的数组的长度
九【代码实现】
- Java语言版
class Solution {public int minCostClimbingStairs(int[] cost) {int n = cost.length;// 动态规划数组int[] dp = new int[n + 1];dp[0] = 0;dp[1] = 0;// 计算爬楼梯的最小花费:到达第 i 层的最小花费由前一层或前两层的最小花费加上当前层的花费决定for (int i = 2; i < (n + 1); i++) {dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);}// 返回结果return dp[n];}
}
- Python语言版
class Solution:def minCostClimbingStairs(self, cost: List[int]) -> int:n = len(cost)# 动态规划数组dp = [0] * (n + 1)# 计算爬楼梯的最小花费:到达第 i 层的最小花费由前一层或前两层的最小花费加上当前层的花费决定for i in range(2, (n + 1)):dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])# 返回结果return dp[n]
- C语言版
int minCostClimbingStairs(int* cost, int costSize)
{// 动态规划数组int* dp = (int *)calloc((costSize + 1), sizeof(int));// 计算爬楼梯的最小花费:到达第 i 层的最小花费由前一层或前两层的最小花费加上当前层的花费决定for (int i = 2; i <= costSize; i++){dp[i] = fmin(cost[i - 1] + dp[i - 1], cost[i - 2] + dp[i - 2]);}int res = dp[costSize];free(dp);// 返回结果return res;
}
十【提交结果】
-
Java语言版

-
Python语言版

-
C语言版

相关文章:

【LeetCode每日一题】——746.使用最小花费爬楼梯
文章目录 一【题目类别】二【题目难度】三【题目编号】四【题目描述】五【题目示例】六【题目提示】七【解题思路】八【时空频度】九【代码实现】十【提交结果】 一【题目类别】 数组 二【题目难度】 简单 三【题目编号】 746.使用最小花费爬楼梯 四【题目描述】 给你一…...

程序里sendStringParametersAsUnicode=true的配置导致sql server cpu使用率高问题处理
一 问题描述 近期生产环境几台sql server从库cpu使用率总是打满,发现抓的带变量值的慢sql,手动代入变量值执行并不慢,秒级返回,不知道问题出在哪里。 二 问题排查 用扩展事件或者sql profiler抓慢sql,抓到了变量值&…...

Vue3 el-table 默认选中 传入的数组
一、效果: 二、官网是VUE2 现更改为Vue3写法 <template><el-table:data"tableData"border striperow-key"id"ref"tableRef":cell-style"{ text-align: center }":header-cell-style"{background: #b7babd…...

最后一个单词的长度
题目详情: 解题思路: 用两个变量分别存储当前值和上次值,就可保证当前移动时记录字符个数,当遇到空格时,这次值保存到上次值,并清空。 代码解析: /* 最后一个单词的长度 */ #include <st…...

2024-11-19 kron积
若A[a11 a12; a21 a22]; B[b11 b12; b21 b22]; 则C[a11*b11 a12*b11 a21*b11 a22*b11; a11*b12 a12*b12 a21*b12 a22*b12; a11*b21 a12*b21 a21*b21 a22*b21; a11*b22 a12*b22 a21*b22 a22*b22] 用MATLAB实现 方法1: A [a11 a12; a21 a22]; B [b11 b12; b21 b22]…...
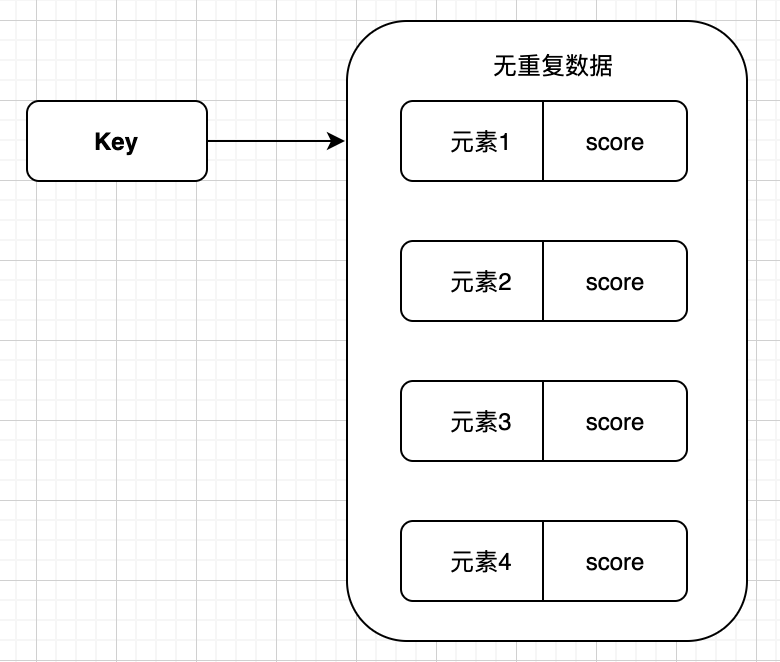
Redis ⽀持哪⼏种数据类型?适⽤场景,底层结构
目录 Redis 数据类型 一、String(字符串) 二、Hash(哈希) 三、List(列表) 四、Set(集合) 五、ZSet(sorted set:有序集合) 六、BitMap 七、HyperLogLog 八、GEO …...

树莓派2 安装raspberry os 并修改成固定ip
安装 安装raspberry os 没啥说的,到树莓派官网,下载制作启动映像盘的软件: https://www.raspberrypi.com/software/ 下载后,直接安装该软件,然后运行,选择好开发板的型号和操作系统型号,按照…...

11月第3周AI资讯
阅读时间:3-4min 更新时间:2024.9.9-2024.9.13 目录 DIAMOND:扩散模型在世界构建中的应用 阿里云推出Qwen2.5-Turbo:高效长文本处理,性价比卓越 微软:AI已实现几乎无限的记忆 Comfyui_Object_Migration一致性换衣模型 DeepSeek发布R1-Lite-Preview:推理AI竞争愈发…...
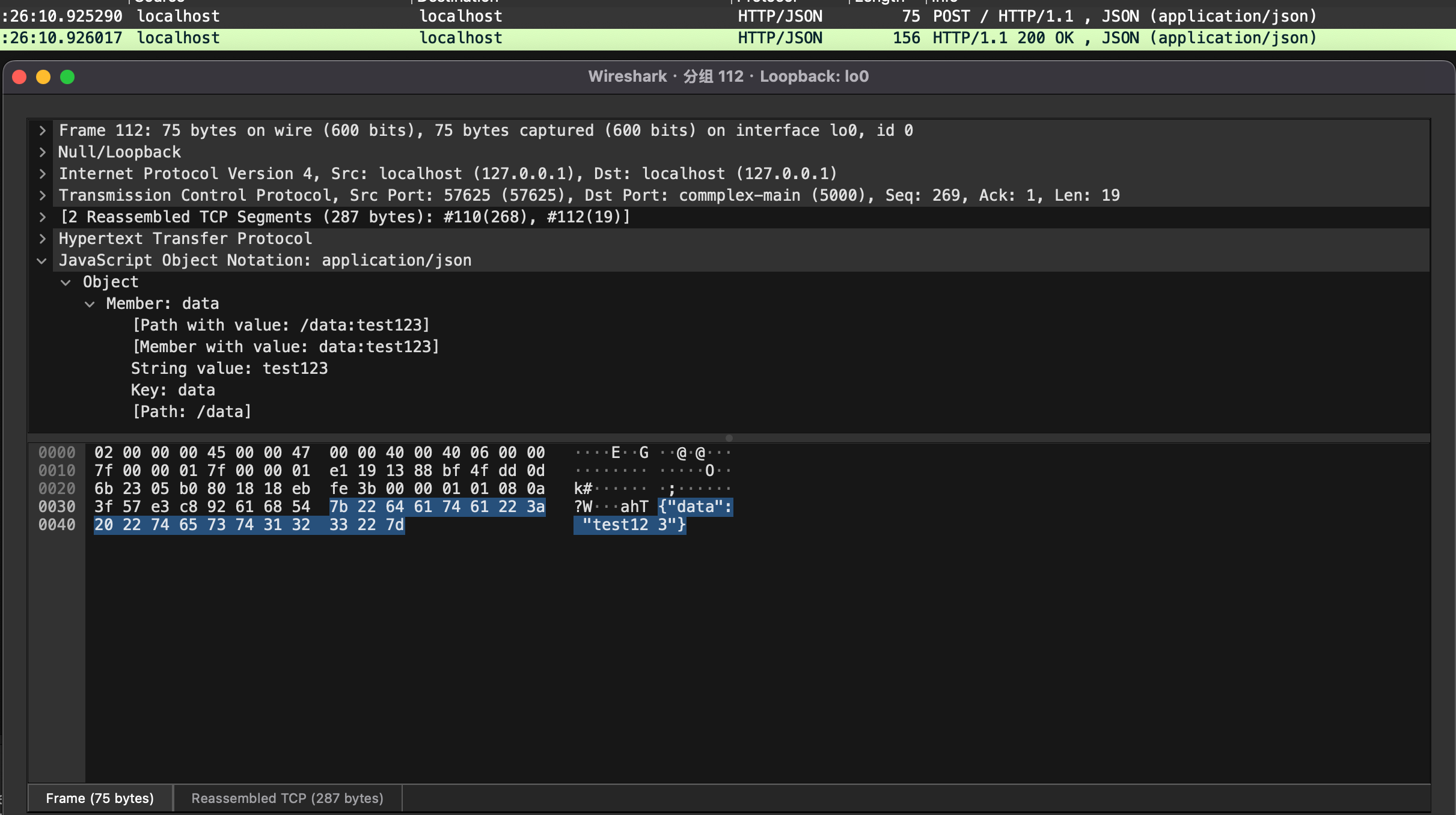
一次封装,解放双手:Requests如何实现0入侵请求与响应的智能加解密
引言 之前写了 Requests 自动重试的文章,突然想到,之前还用到过 Requests 自动加解密请求的逻辑,分享一下。之前在做逆向的时候,发现一般医院的小程序请求会这么玩,请求数据可能加密也可能不加密,但是返回…...

Notepad++--在开头快速添加行号
原文网址:Notepad--在开头快速添加行号_IT利刃出鞘的博客-CSDN博客 简介 本文介绍Notepad怎样在开头快速添加行号。 需求 原文件 想要的效果 方法 1.添加点号 Alt鼠标左键,从首行选中首列下拉,选中需要添加序号的所有行的首列ÿ…...

Python和MATLAB示例临床因素分析
🌵Python片段 为了演示临床因素的分析,让我们模拟一个数据集并执行一些基本的统计和机器学习分析。我们将重点关注以下步骤: 模拟数据集:创建具有年龄、性别、BMI、吸烟状况和疾病结果等特征的临床数据。描述性统计:…...

嵌入式硬件实战基础篇(二)-稳定输出3.3V的太阳能电池-无限充放电
引言:本内容主要用作于学习巩固嵌入式硬件内容知识,用于想提升下述能力,针对学习稳压芯片和电容以及电池之间的运用,对于硬件PCB以及原理图的练习和前面硬件篇的实际运用;太阳能是一种清洁、可再生的能源,广…...

【数据结构】树——链式存储二叉树的基础
写在前面 书接上文:【数据结构】树——顺序存储二叉树 本篇笔记主要讲解链式存储二叉树的主要思想、如何访问每个结点、结点之间的关联、如何递归查找每个结点,为后续更高级的树形结构打下基础。不了解树的小伙伴可以查看上文 文章目录 写在前面 一、链…...

STM32-- keil常见报错与解决办法
调试问题 1. keil在线调试需要点击好几次运行才可以运行,要是直接下载程序直接就不运行。 解决:target里面的use microlib要勾选,因为使用了printf。 keil在线调试STM32,点三次运行才能跑到main的问题解决。 keil在线调试STM32…...
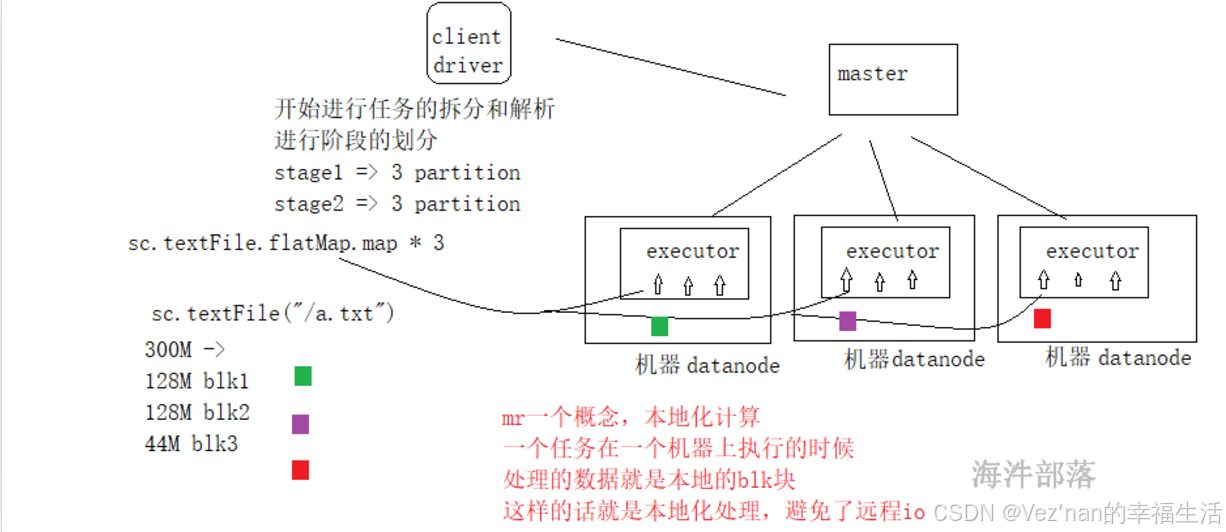
【大数据学习 | Spark-Core】RDD的概念与Spark任务的执行流程
1. RDD的设计背景 在实际应用中,存在许多迭代式计算,这些应用场景的共同之处是,不同计算阶段之间会重用中间结果,即一个阶段的输出结果会作为下一个阶段的输入。但是,目前的MapReduce框架都是把中间结果写入到HDFS中&…...

一文读懂埋阻埋容工艺
PCB 埋阻埋容工艺是一种在 PCB 板内部埋入电阻和电容的工艺。通常情况下, PCB 上电阻和电容都是通过贴片技术直接焊接在板面上的,而埋阻埋容工艺则将电 阻和电容嵌入到 PCB 板的内部层中,这种印制电路板,其自下而上依次包括第一介电 层,隐埋电…...
)
mysql 数据表导出为 markdown(附 go 语言 gorm 的实际使用)
前言 通常业务系统开发中,数据库的设计与维护是至关重要的环节。而数据库的文档化则是确保团队成员之间有效沟通、快速理解系统架构的基础。 但目前数据文档都是手动写的,耗时费力,由于当前项目使用的是 mysql 作为存储引擎,找找…...

本地云存储 MinIO 中修改用户密码
本地云存储 MinIO 中修改用户密码 MinIO 中修改用户密码前提条件步骤 1:安装 MinIO Client对于 Linux/macOS:对于 Windows: 步骤 2:配置 MinIO Client步骤 3:查看现有用户步骤 4:修改用户密码步骤 5&#x…...

go项目中比较好的实践方案
工作两年来,我并未遇到太大的挑战,也没有特别值得夸耀的项目。尽管如此,在日常的杂项工作中,我积累了不少心得,许多实践方法也在思考中逐渐得到优化。因此,我在这里记录下这些心得。 转发与封装 这个需求…...
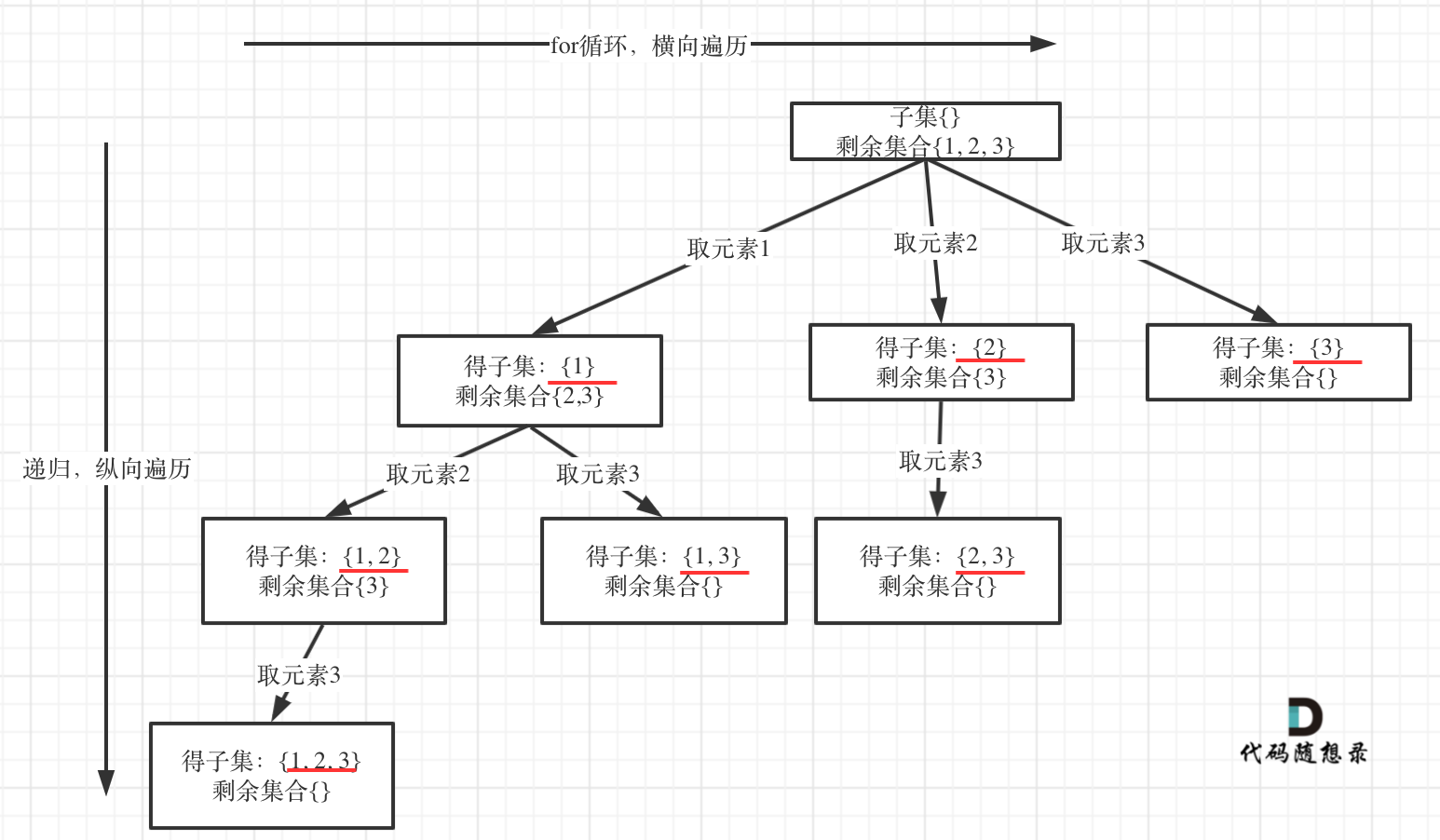
回溯法基础入门解析
回溯法 前 言 回溯法也可以叫做回溯搜索法,它是一种搜索的方式。回溯是递归的副产品,只要有递归就会有回溯。回溯法,一般可以解决如下几种问题: 组合问题:N个数里面按一定规则找出k个数的集合切割问题:一…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...

Python爬虫实战:研究Restkit库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的有价值数据。如何高效地采集这些数据并将其应用于实际业务中,成为了许多企业和开发者关注的焦点。网络爬虫技术作为一种自动化的数据采集工具,可以帮助我们从网页中提取所需的信息。而 RESTful API …...
