在 Sublime Text 中直接预览 Markdown 文件
在 Sublime Text 中直接预览 Markdown 文件需要借助插件实现。以下是详细步骤:
1. 安装 Markdown Preview 插件
- 按下快捷键
Ctrl+Shift+P(或 macOS 上的Cmd+Shift+P),打开命令面板。 - 输入
Install Package并选择Package Control: Install Package。 - 等待包列表加载完成后,搜索
Markdown Preview并点击安装。
2. 使用 Markdown Preview
- 打开需要预览的
.md文件。 - 按下快捷键
Ctrl+Shift+P(或 macOS 上的Cmd+Shift+P) 打开命令面板。 - 搜索
Markdown Preview: Preview in Browser或Markdown Preview: Export HTML,选择其中一个:
- Preview in Browser:在默认浏览器中预览。
- Export HTML:将 Markdown 文件导出为 HTML 文件。
3. 启用实时预览(可选)
如果需要实时预览效果,可以结合浏览器插件或其他实时预览工具,比如:
- Typora(独立工具):支持实时 Markdown 编辑和预览。
- 浏览器扩展:如 Chrome 的
Markdown Viewer插件。
4. 其他 Markdown 插件
如果需要更多 Markdown 功能,可以尝试以下插件:
- MarkdownEditing:优化 Markdown 的语法高亮和编辑体验。
- AdvancedNewFile:方便快速创建
.md文件。
相关文章:

在 Sublime Text 中直接预览 Markdown 文件
在 Sublime Text 中直接预览 Markdown 文件需要借助插件实现。以下是详细步骤: 1. 安装 Markdown Preview 插件 按下快捷键 CtrlShiftP (或 macOS 上的 CmdShiftP),打开命令面板。输入 Install Package 并选择 Package Control: Install Package。等待包…...

分词器的概念(通俗易懂版)
什么是分词器?简单点说就是将字符序列转化为数字序列,对应模型的输入。 通常情况下,Tokenizer有三种粒度:word/char/subword word: 按照词进行分词,如: Today is sunday. 则根据空格或标点进行分割[today, is, sunda…...

速通前端篇 —— CSS
找往期文章包括但不限于本期文章中不懂的知识点: 个人主页:我要学编程程(ಥ_ಥ)-CSDN博客 所属专栏:速通前端 目录 CSS的介绍 基本语法规范 CSS选择器 标签选择器 class选择器 id选择器 复合选择器 通配符选择器 CSS常见样式 颜…...

数据库表设计范式
华子目录 MYSQL库表设计:范式第一范式(1NF)第二范式(2NF)第三范式(3NF)三范式小结巴斯-科德范式(BCNF)第四范式(4NF)第五范式(5NF&…...
经济增长初步
1.人均产出 人均产出,通常指的是一个国家、地区或组织在一定时期内,每个劳动人口平均创造的生产总值。它是衡量一个地区或国家经济效率和劳动生产率的重要指标。具体来说,人均产出可以通过以下公式计算: 人均产出总产出/劳动人口…...

【架构】主流企业架构Zachman、ToGAF、FEA、DoDAF介绍
文章目录 前言一、Zachman架构二、ToGAF架构三、FEA架构四、DoDAF 前言 企业架构(Enterprise Architecture,EA)是指企业在信息技术和业务流程方面的整体设计和规划。 最近接触到“企业架构”这个概念,转念一想必定和我们软件架构…...

时间请求参数、响应
(7)时间请求参数 1.默认格式转换 控制器 RequestMapping("/commonDate") ResponseBody public String commonDate(Date date){System.out.println("默认格式时间参数 date > "date);return "{module : commonDate}"; }…...

PyTorch图像预处理:计算均值和方差以实现标准化
在深度学习中,图像数据的预处理是一个关键步骤,它直接影响模型的训练效果和收敛速度。PyTorch提供的transforms.Normalize()函数允许我们对图像数据进行标准化处理,即减去均值并除以方差。这一步骤对于提高模型性能至关重要。 为什么需要标准…...
slice介绍slice查看器
Android Jetpack架构组件(十)之Slices - 阅读清单 - 腾讯云开发者社区-腾讯云 slice 查看器apk 用adb intall 安装 Releases android/user-interface-samples GitHubMultiple samples showing the best practices in the user interface on Android. - Releases android/u…...

Android音频采集
在 Android 开发领域,音频采集是一项非常重要且有趣的功能。它为各种应用程序,如语音聊天、音频录制、多媒体内容创作等提供了基础支持。今天我们就来深入探讨一下 Android 音频采集的两大类型:Mic 音频采集和系统音频采集。 1. Mic音频采集…...
通过轻易云平台实现聚水潭数据高效集成到MySQL的技术方案
聚水潭数据集成到MySQL的技术案例分享 在本次技术案例中,我们将详细探讨如何通过轻易云数据集成平台,将聚水潭的数据高效、可靠地集成到MySQL数据库中。具体方案为“聚水谭-店铺查询单-->BI斯莱蒙-店铺表”。这一过程不仅需要处理大量数据的快速写入…...

类和对象( 中 【补充】)
目录 一 . 赋值运算符重载 1.1 运算符重载 1.2 赋值运算符重载 1.3 日期类实现 1.3.1 比较日期的大小 : 1.3.2 日期天数 : 1.3.3 日期 - 天数 : 1.3.4 前置/后置 1.3.5 日期 - 日期 1.3.6 流插入 << 和 流提取 >> 二 . 取地址运算符重载 2.1 const…...
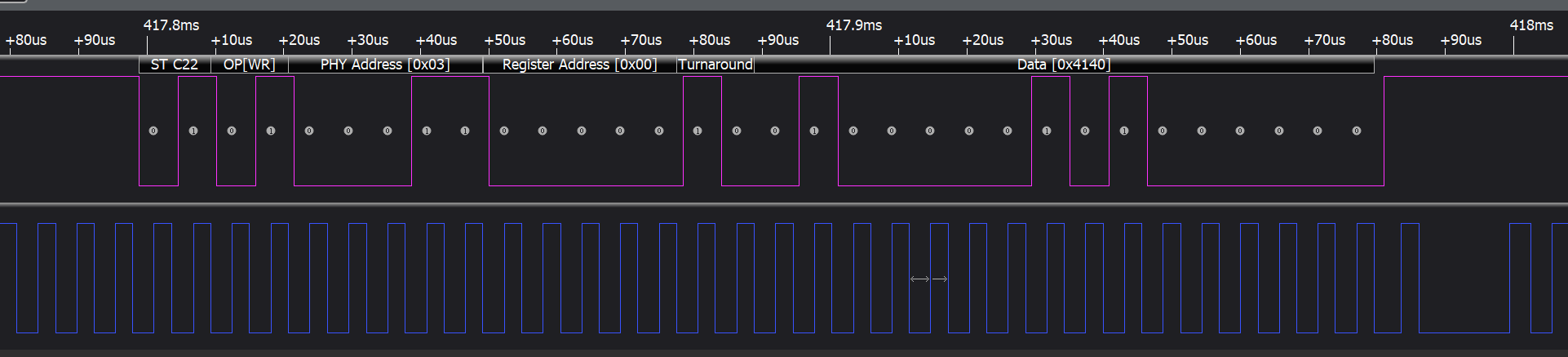
如何使用gpio模拟mdio通信?
一、前言 实际项目开发中,由于设计原因,会将phy的mdio引脚连接到SoC的2个空闲gpio上, 这样就无法通过Gmac自有的架构实现修改phy, 因此只能通过GPIO模拟的方式实现MDIO, 好在Linux支持MDIO via GPIO功能。 该功能…...

C# 中的事件和委托:构建响应式应用程序
C#中的事件和委托。事件和委托是C#中用于实现观察者模式和异步回调的重要机制,它们在构建响应式和交互式应用程序中发挥着重要作用。以下是一篇关于C#中事件和委托的文章。 引言 事件和委托是C#语言中非常重要的特性,它们允许你实现观察者模式和异步回…...

科技赋能健康:多商户Java版商城系统引领亚健康服务数字化变革
在当今社会,随着生活节奏的加快和工作压力的增大,越来越多的人处于亚健康状态。据《The Lancet》期刊2023年的统计数据显示,全球亚健康状态的人群比例已高达82.8%,这一数字背后,隐藏着巨大的健康风险和社会成本。亚健康…...
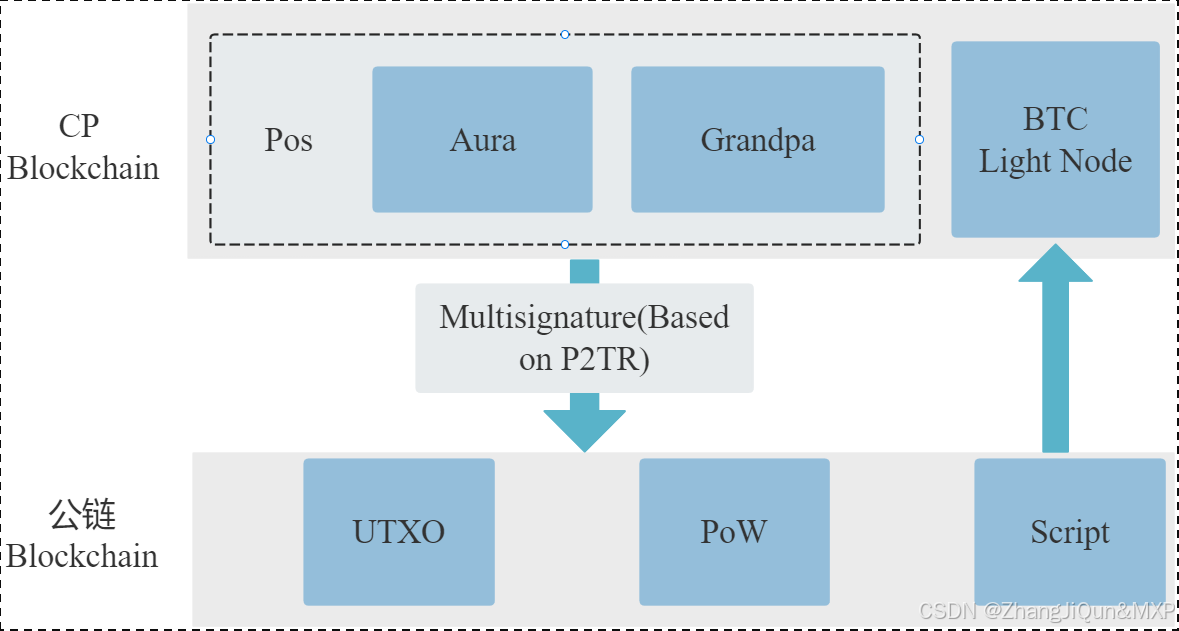
区块链网络示意图;Aura共识和Grandpa共识(BFT共识)
目录 区块链网络示意图 Aura共识和Grandpa共识(BFT共识) Aura共识 Grandpa共识(BFT共识) Aura与Grandpa的结合 区块链网络示意图 CP Blockchain:这是中央处理区块链(或可能指某种特定的处理单元区块链)的缩写。它可能代表了该区块链网络的主要处理或存储单元。在这…...
Javaweb梳理18——JavaScript
今日目标 掌握 JavaScript 的基础语法掌握 JavaScript 的常用对象(Array、String)能根据需求灵活运用定时器及通过 js 代码进行页面跳转能通过DOM 对象对标签进行常规操作掌握常用的事件能独立完成表单校验案例 18.1 JavaScript简介 JavaScript 是一门跨…...

面向对象-接口的使用
1. 接口的概述 为什么有接口? 借口是一种规则,对于继承而言,部分子类之间有共同的方法,为了约束方法的使用,使用接口。 接口的应用: 接口不是一类事物,它是对行为的抽象。 2. 接口的定义和使…...
)
失落的Apache JDBM(Java Database Management)
简介 Apache JDBM(Java Database Management)是一个轻量级的、基于 Java 的嵌入式数据库管理系统。它主要用于在 Java 应用程序中存储和管理数据。这个项目已经过时了,只是发表一下以示纪念,现在已经大多数被SQLite和Derby代替。…...
Vue3+SpringBoot3+Sa-Token+Redis+mysql8通用权限系统
sa-token支持分布式token 前后端代码,地球号: bright12389...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...
