24软专 数据结构
1、A[n],k,将数组向右循环移动k位。要求时间复杂度O(n),空间O(1)。
思路:采用三次反转数组的操作,可以实现时间复杂度为O(n),空间复杂度为O(1)的算法。
void moveElem(int array[],int k,int length){//array是需要循环移动元素的数组,k是需要移动的位数,length是数组的长度int temp;//先将整个数组反转for(int i=0;i<=length/2;i++){temp=array[length-1-i];array[length-1-i]=array[i];array[i]=temp;}//再反转前K个元素,这样就使得原本在倒数k个位置的元素来到了数组前K个位置,相当于后k个元素都前进了k位for(int i=0;i<=k/2;i++){temp=array[k-1-i];array[k-1-i]=array[i];array[i]=temp;}//再反转下标为k到n-1的所有元素,相当于前n-k个元素后移了k位for(int i=k;i<=(length+k)/2-1;i++){temp=array[length+k-1-i];array[length+k-1-i]=array[i];array[i]=temp;}
}2、给定一个无向无权图G,对所有顶点排序,按照每个顶点到顶点V的最短路径长度非增排序。要求时间复杂度O(n+e) n:顶点数 e:边数
bool visited[MaxVertexNum]; // 访问数组
char distSorted[MaxVertexNum]; // 保存排序信息
int len; // 路径长度(或者理解为广度优先搜素层数)
void BFSTraverse(ALGraph G, int K, int v) // 邻接表存储图
{for (int i = 0; i < G.vernum; ++i){visited[i] = false; // 初始化访问数组dist[i] = -1; // 初始化最短路径数组}Queue Q;InitQueue(Q); // 初始化队列;// 从顶点V开始搜索// 更新访问数组visited[v] = true;distSorted[0] = G.vertices[v].data;int i=0;// 将结点V入队EnQueue(Q, v);while (!IsEmpty(Q)){ // 当队列不空时DeQueue(Q, v); // 队首顶点出队并用V保存该顶点for (ArcNode *p = G.vertices[v].firstarc; p; p->nextarc){ // 检测所有V的邻接点int w = p->adjvex; // w即为邻接点if (visited[w] == false){ // 当前节点未访问// 更新访问数组visited[w] = true;distSorted[++i] = G.vertices[v].data;EnQueue(Q, w); // w入队}}}//给结点排序,由于广度优先搜索形成的结点是按照距离由小到大保存的,因此只要反转数组即可for(int i=0;i<=G.vernum/2;i++){char temp=distSorted[G.vernum-1-i];distSorted[G.vernum-1-i]=distSorted[i];distSorted[i]=temp;}
}3、struct BinNode{
int size;//以该结点为根的子树的总结点数
BinNode *left,*right;
}
实现BinNode* rank(BinNode *t,int k)
功能为找到先根序列中第K个结点,返回其地址。要求:不使用先序遍历,且时间复杂度为0(depth(x)),depth(x)为结点x的深度。
BinNode *rank(BinNode *t, int k)
{if (!t)return nullptr; // 如果树为空,返回空// 如果第k个节点就是当前节点if (k == 1)return t;// 如果第k个节点在左子树中if (k <= t->left->size+1){return rank(t->left, k-1);}else{// 如果第k个节点在右子树中return rank(t->right, k - t->left->size - 1);}
}按照先序遍历的规则,根节点是先序遍历中的第1个节点,然后先遍历完左子树才会遍历右子树,因此如果k小于左子树上节点的个数,那么说明第k个节点在其左子树上,因此继续往左寻找。而如果k大于左子树上的节点个数就说明k在右子树上,因此向右寻找。
相关文章:

24软专 数据结构
1、A[n],k,将数组向右循环移动k位。要求时间复杂度O(n),空间O(1)。 思路:采用三次反转数组的操作,可以实现时间复杂度为O(n),空间复杂度为O(1)的算法。 void moveElem(int array[],int k,int length){//a…...

洛谷 P1616 疯狂的采药 C语言 记忆化搜索
题目: https://www.luogu.com.cn/problem/P1616?contestId215526 完全背包问题,最后一个超出空间了。完全背包和就是无限次的拿,公式跟01背包差不多。 但是,只有当前能拿和拿不下,换下一个。注意要处理好边界条件。…...

#渗透测试#红蓝攻防#HW#SRC漏洞挖掘01之静态页面渗透
免责声明 本教程仅为合法的教学目的而准备,严禁用于任何形式的违法犯罪活动及其他商业行为,在使用本教程前,您应确保该行为符合当地的法律法规,继续阅读即表示您需自行承担所有操作的后果,如有异议,请立即停…...

element-plus入门教程:Button
一、Button组件概述 Element Plus的Button组件是一个常用的操作按钮,提供了多种类型、尺寸、状态等配置选项,以满足不同的交互需求。 二、安装Element Plus 在Vue 3项目中,可以通过npm或yarn来安装Element Plus。 npm install element-pl…...

oneplus6线刷、trwp、magisk(apatch)、LSPosed、Shamiko、Hide My Applist
oneplus6线刷android10.0.1 oneplus6线刷包(官方android10.0.1)下载、线刷教程: OnePlus6-brick-enchilada_22_K_52_210716_repack-HOS-10_0_11-zip 启用开发者模式 设置 / 连续点击6次版本号 : 启用开发者模式设置/开发者模式/{打开 usb调试, 打开 网络adb调试,…...
flux的版本
1.flux1-dev.safetensors https://huggingface.co/black-forest-labs/FLUX.1-devhttps://huggingface.co/black-forest-labs/FLUX.1-dev原生的23.8G的模型。原生12B的模型,float16的。需要配合ae.safetensors,flux1-dev.safetensors以及clip-l和T5的权重使用,注意ae.sft和f…...

Kafka 数据倾斜:原因、影响与解决方案
Kafka:分布式消息系统的核心原理与安装部署-CSDN博客 自定义 Kafka 脚本 kf-use.sh 的解析与功能与应用示例-CSDN博客 Kafka 生产者全面解析:从基础原理到高级实践-CSDN博客 Kafka 生产者优化与数据处理经验-CSDN博客 Kafka 工作流程解析:…...
【从零开始的LeetCode-算法】3297. 统计重新排列后包含另一个字符串的子字符串数目 I
给你两个字符串 word1 和 word2 。 如果一个字符串 x 重新排列后,word2 是重排字符串的 前缀,那么我们称字符串 x 是 合法的 。 请你返回 word1 中 合法 子字符串的数目。 示例 1: 输入:word1 "bcca", word2 "…...

【2024APMCM亚太赛A题】完整参考论文与代码分享
A题 一、问题重述二、问题分析问题一:水下图像分类问题二:退化原因建模问题三:针对单一退化的图像增强方法问题四:复杂场景的综合增强模型问题五:针对性增强与综合增强的比较 三、问题假设退化特征独立性假设物理模型普…...
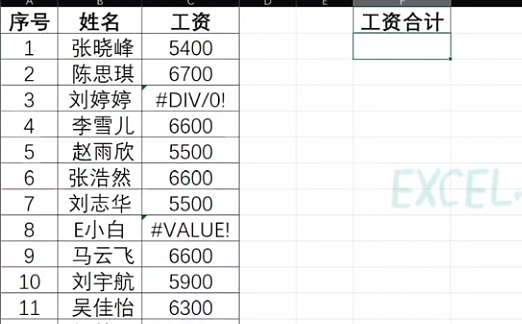
Excel求和如何过滤错误值
一、问题的提出 平时,我们在使用Excel时,最常用的功能就是求和了,一说到求和你可能想到用sum函数,但是如果sum的求和区域有#value #Div等错误值怎么办?如下图,记算C列中工资的总和。 直接用肯定会报错&…...

Android 常用命令和工具解析之GPU相关
目录 1、GPU基本信息 1.1 获取GPU基本信息 1.2 伪造GPU基本信息 2、GPU内存信息 3、经典案例 案例1:GPU伪造信息方案 案例2:GPU内存统计算法 GPU 指的是 Graphics Processing Unit,即图形处理单元。GPU 是一种专门用于处理图形和图像相…...

刷题——【模板】二维前缀和
前缀和 题目题目链接题解方法一方法二 题目 描述 给你一个 n 行 m 列的矩阵 A ,下标从1开始。 接下来有 q 次查询,每次查询输入 4 个参数 x1 , y1 , x2 , y2 请输出以 (x1, y1) 为左上角 , (x2,y2) 为右下角的子矩阵的和, 输入描述&#x…...

Xilinx 7 系列 FPGA的各引脚外围电路接法
Xilinx 7系列FPGA的外围电路接法涉及到多个方面,包括电源引脚、时钟输入引脚、FPGA配置引脚、JTAG调试引脚,以及其他辅助引脚。 本文参考资料: ds180 - 7 Series FPGAs Data Sheet - Overview ds181 - Artix 7 FPGAs Data Sheet - DC and AC…...
基础 | 目标网站)
Python 爬虫 (1)基础 | 目标网站
一、目标网站 1、加密网站 1.1、关键字比较明确 企名片:https://wx.qmpsee.com/articleDetail?idfeef62bfdac45a94b9cd89aed5c235be 1.2、关键字比较泛 烯牛数据:https://www.xiniudata.com/project/event/lib/invest...

数字后端零基础入门系列 | Innovus零基础LAB学习Day11(Function ECO流程)
###LAB 20 Engineering Change Orders (ECO) 这个章节的学习目标是学习数字IC后端实现innovus中的一种做function eco的flow。对于初学者,如果前面的lab还没掌握好的,可以直接跳过这节内容。有时间的同学,可以熟悉掌握下这个flow。 数字后端…...

量子卷积神经网络
量子神经网络由量子卷积层、量子池化层和量子全连接层组成 量子卷积层和量子池化层交替放置,分别实现特征提取和特征降维,之后通过量子全连接层进行特征综合 量子卷积层、量子池化层和量子全连接层分别由量子卷积单元、量子池化单元和量子全连接单元组…...

储能电站构成及控制原理
系列文章目录 能量管理系统(EMS)储能充放电策略 文章目录 系列文章目录一、储能电站构成二、储能系统关键部件及作用1.电池储能系统2.功率变换系统(Power Conversion System,PCS)3.变配电系统4.后台监控系统5.继电保护及安全自动装置 三、储能电站的功能四、储能电站控制策略 …...

Rocky Linux 系统安装/部署 Docker
1、下载docker-ce的repo文件 [rootlocalhost ~]# curl https://download.docker.com/linux/centos/docker-ce.repo -o /etc/yum.repos.d/docker.repo % Total % Received % Xferd Average Speed Time Time Time Current Dloa…...

12 —— Webpack中向前端注入环境变量
需求:开发模式下打印语句生效,生产模式下打印语句失效 使用Webpack内置的DefinePlugin插件 const webpack require(webpack) module.exports { plugins: [ new webpack.DefinePlugin({ process.env.NODE_ENV:JSON.stringify(process.env.NODE_ENV) }…...

uniapp接入BMapGL百度地图
下面代码兼容安卓APP和H5 百度地图官网:控制台 | 百度地图开放平台 应用类别选择《浏览器端》 /utils/map.js 需要设置你自己的key export function myBMapGL1() {return new Promise(function(resolve, reject) {if (typeof window.initMyBMapGL1 function) {r…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...
